基于靜態法高速列車抗橫風傾覆影響因素研究*

羅祿林 楚琦星 賈永興 牛 軍 梅元貴

(蘭州交通大學機電工程學院,730070,蘭州∥第一作者,碩士研究生)

基于靜態法高速列車抗橫風傾覆影響因素研究*

羅祿林 楚琦星 賈永興 牛 軍 梅元貴

(蘭州交通大學機電工程學院,730070,蘭州∥第一作者,碩士研究生)

隨著我國高速鐵路的飛速發展,風區運營的高速鐵路不斷出現,需對高速列車的抗橫風傾覆性能進行深入研究。在對比分析日本的國枝方法和日比野有方法的基礎上,針對我國CRH5H型動車組建立了橫風傾覆靜態計算模型,并對車體自重、轉向架一系及二系懸掛剛度對列車抗傾覆性能的影響進行了數值模擬。數值計算結果符合實際規律,計算模型和方法可為風區運營車輛抗傾覆安全設計提供參考。

高速列車; 傾覆穩定性; 靜態方法

Author′s address School of Mechanical and Electrical Engineering, Lanzhou JiaoTong University,730070,Lanzhou,China

隨著我國高速鐵路的不斷發展,風區運營線路不斷出現。我國幅員遼闊,各地區風場環境差異巨大。氣象統計結果表明,京滬高鐵沿線各站20 m/s級別日極大風速的發生概率為81%～100%,百年一遇日極大風速達到38 m/s[1]。京津城際鐵路沿線春冬季瞬時最大風速可達31.6 m/s[2]。目前已建成運營的蘭州至烏魯木齊第二雙線全長1 776 km,其中近580 km線路在風區運行。蘭新高鐵沿線通過新疆境內的百里風區、三十里風區、煙墩風區、達坂城風區和甘肅境內的安西風區,其中百里風區大于8級風的大風天數超過百天,風速最高可達64 m/s[3-4]。大風多次引起既有蘭新鐵路中斷行車,甚至列車脫線、翻車等重大事故[5],給鐵路運輸造成巨大損失。強風給風區運行高速列車帶來了極大的安全隱患,因此有必要對高速列車橫風環境安全運行性能進行研究。

文獻[6]采用靜態方法給出了列車在橫風作用下的傾覆系數計算公式,即國枝式。文獻[7-8]改進了國枝式,考慮了轉向架中更多懸掛部件的影響。文獻[9]建立了車輛傾覆的靜態模型,對普速列車大風環境下傾覆特性進行了研究。靜態法建模快速簡單，對計算工具的要求低。

文獻[10-12]運用多體動力學仿真商業軟件研究了大風作用下列車的傾覆性能。多體動力學仿真商業軟件能夠對影響車輛傾覆的各部件進行多自由度數值模擬,但其建模過程復雜,資源耗費大。文獻[13]使用準靜態方法得到了與多體動力學仿真商業軟件結果媲美的計算結果,其建模過程相比靜態方法同樣較為復雜。

本文針對我國蘭新高鐵第二雙線運營的CRH5H型動車組，建立了基于KUNIEDA[6]和YU HIBINO[7-8]的兩種橫風傾覆靜態計算模型,并對影響列車傾覆的多種參數進行研究,以期為我國風區運營高速列車抗傾覆安全設計提供參考。

1 數學模型

CRH5H高寒抗風沙動車組為滿足長期在8級至12級強風沙環境運行設計[14]。其機械材料、密封橡膠、油脂以及電氣元件等在前期設計中充分考慮了低溫適應性能,并特別針對大風安全傾覆及側窗玻璃抗礫石沖擊安全等進行計算或試驗驗證。為提高抗傾覆性能,CRH5H動車組轉向架設置了抗側滾扭桿。

車輛傾覆一般可分為三種情況:①曲線外側傾覆,當車輛位于曲線軌道上運行時,在最不利外力組合作用下,向曲線軌道外側發生傾覆;②曲線內側傾覆,當車輛以較低速度行駛于曲線軌道上時,由于曲線軌道有外超高,使得列車向內傾,同時受到向內側力(風力、振動慣性力)作用,使得車輛向曲線內側傾覆;③平直軌道傾覆,車輛在直線軌道上運行,受到大風作用或者同時遭受由于線路不平順等原因造成的車輛橫向劇烈振動的橫向慣性力的作用而引起車輛向一側傾覆。本文建模過程中考慮曲線外側傾覆,且以半車模型建模。在不考慮超高時,計算模型可用于直線軌道傾覆的計算。

車輛抗傾覆性能可用車輛迎風側車輪減載程度來衡量,即傾覆系數[15]。

(1)

式中:

Q0——靜態輪重;

ΔQ——迎風側輪重減少量;

P1——迎風側輪軌間垂向作用力;

P2——背風側輪軌間垂向作用力。

1.1 國枝方法

車輛位于彎道上時受到的外力如圖 1所示。受力分析時主要考慮:①車輛通過曲線時未被平衡的離心力,其中包括車輛通過曲線時的離心力與外軌超高引起的重力在離心力方向上的分力;②車輛橫向振動慣性力;③橫風作用在車輛上產生的橫向氣動力、氣動升力。

推導車輛傾覆系數公式時,國枝方法假設:

(1) 不考慮由于車體傾斜造成的各側向力的作用點距離軌面的垂直高度的變化;

(2) 不考慮車輛簧下部分所受氣動力的影響;

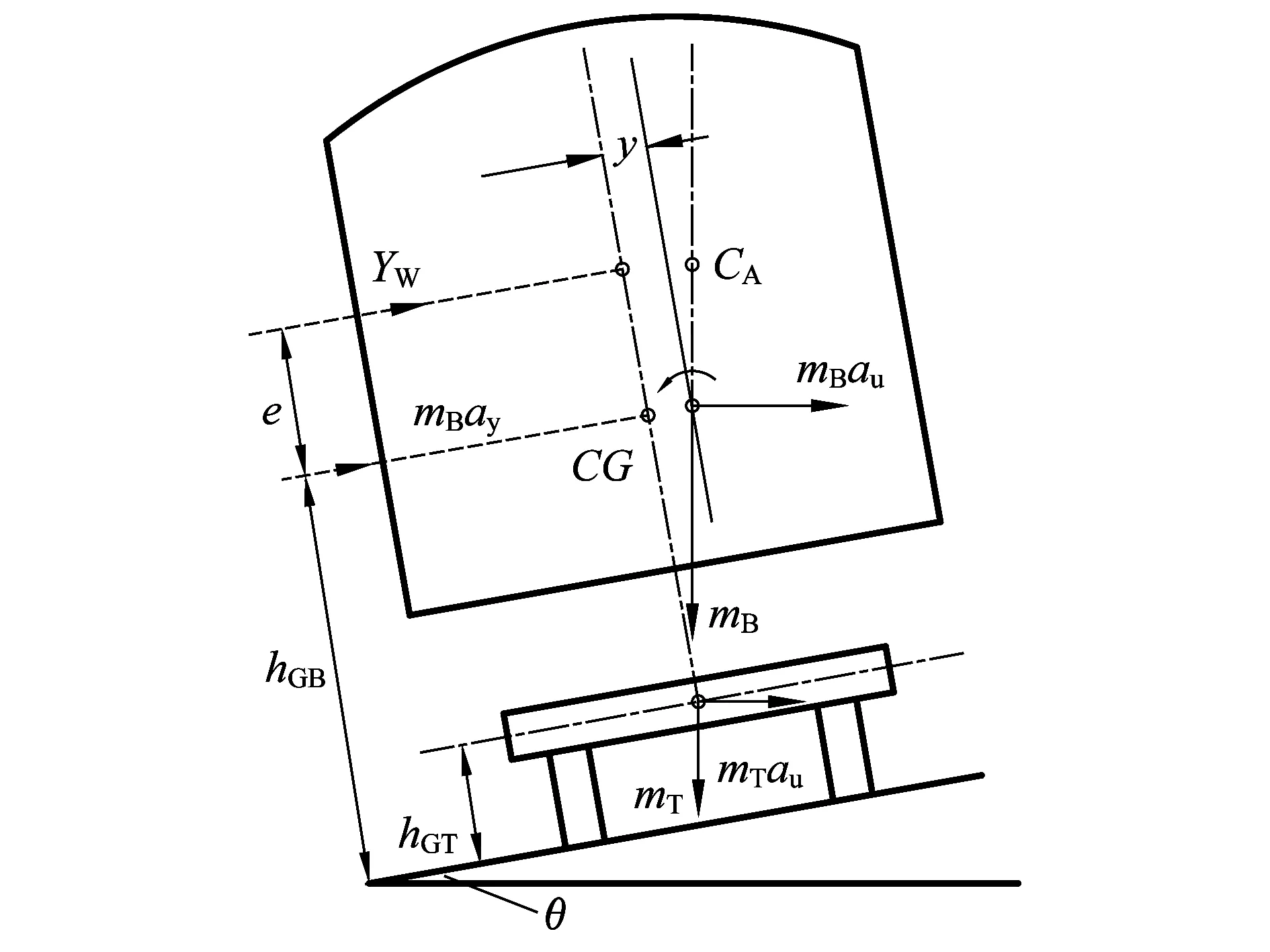
圖1 車輛過曲線時的受力狀態

(3) 不考慮車輛簧上質量垂直振動慣性力的影響;

(4) 不考慮車輛簧下質量垂向和橫向振動慣性力的影響,并假定簧下質量的重心位于輪對中心;

(5) 由于高速鐵路曲線半徑相對于車體長度較大,車鉤力方向偏移車鉤中心線方向較小,因此不考慮車鉤力。

(6) 不考慮輪對踏面在軌面上的滑移;

(7) 將橫風引起的橫向力集中于風壓中心。

根據靜態力矩平衡原理,列車傾覆系數可表示為:

(2)

式中:

μ——轉向架質量mT與半車體質量mB之比;

v——車速;

R——線路曲線半徑;

c——軌道外超高;

YW——氣動力;

hGB——車體重心距軌面高度;

hBC——風壓中心距軌面高度;

hGT——轉向架重心距軌面高度;

G——輪軌接觸點橫向跨距;

g——重力加速度;

e——風壓中心至車體重心間的距離;

cy——單位橫向力引起的車體重心橫向位移,cy=1/(2Ky),其中Ky為每個轉向架彈簧的橫向剛度;

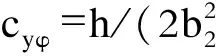
圖1中,車體重心橫向位移y=cyY+cyφM,其中Y為橫向力，M為側滾力矩。

1.2 日比野有靜態方法

日比野有[7]在國枝公式基礎上,考慮車體重心在兩級懸掛作用下的橫向位移和側滾角位移,建立了日比野有靜態方法(以下簡為“靜態方法”)。靜態方法與國枝方法的不同點在于:

(1) 更多地考慮了轉向架的彈性元件的影響;

(2) 對于外力引起的車體重心位移的變化,除了考慮橫向位移變化之外,還考慮了繞重心的側滾位移。

車輛位于曲線軌道上時受力模型如圖2所示。對背風側輪軌接觸點取矩,有:

hGTmTau-hGB(mBau+mBay)-hBCFS

(3)

式中:

FS——橫向力;

FL——氣動升力;

mB——半車體質量;

ay——車體橫向振動加速度;

au——超離心加速度;

hBC——風壓中心距軌面高度;

hGB——車體重心距軌面高度;

yB——車體重心橫向位移;

ΦB——車體側滾角位移。

由式(3)可得計算傾覆系數計算公式:

(4)

式(4)中,yB、ΦB與FB(FB=FS+mBau+mBay)和繞車體重心的側滾力矩MB(MB=-eFB)之間的關系可按以下線性關系式定義:

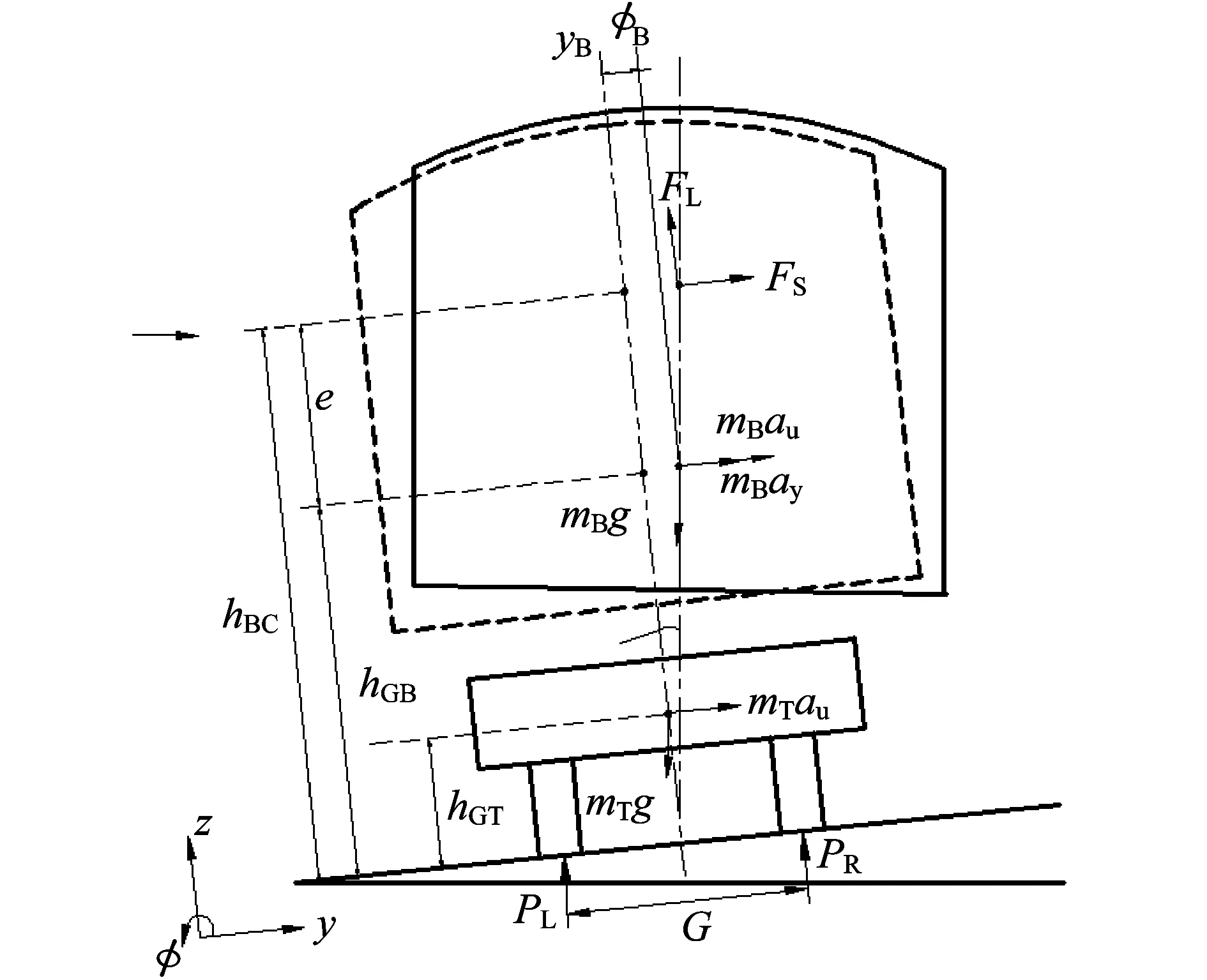
圖2 日比野有車輛傾覆模型

yB≡CyFB+DyMB+yB0

ΦB≡CΦFB+DΦMB+ΦB0

(5)

式中:

Cy——每單位橫向力的重心橫向位移;

Dy——每單位力矩的重心橫向位移;

CΦ——每單位橫向力的重心側滾位移;

DΦ——每單位力矩的重心側滾位移;

yB0，ΦB0——止擋影響項。

Cy、Dy、CΦ、DΦ為彈簧系統影響系數。

受到外力作用的車體在軸向彈簧附近產生側滾角位移Φ1,在空氣彈簧附近產生側滾角位移Φ2,并在空氣彈簧橫向剛度作用下產生橫向位移y2,這些位移相互疊加得到車體重心的橫向位移yB、側滾角位移ΦB及垂向位移zB,如式(6)所示。

(6)

式中：

h1——車體重心至輪軸中心的距離;

h2——車體重心至空氣彈簧中心的距離。

車體在臨界傾覆狀態下,忽略車體重心各項位移儲存的勢能三次以上的項,同時考慮是否碰撞橫向止擋和垂向止擋,根據虛功原理忽略二次以上無窮小項,可以得到車體重心的各項位移；將結果代入式(5)和式(6),便可得到式(4)中的yB和ΦB。

對于CRH5H高寒抗風沙動車組轉向架,推導可得彈簧系統影響系數表達式為:

其中

hs=h1-h2-h3

式中:

h3——橫向止擋中心到輪軸中心線的距離;

kys——橫向止擋剛度;

ky——空氣彈簧橫向剛度;

k1——軸向彈簧垂向剛度;

k2——空氣彈簧垂向剛度;

kr——抗側滾扭桿剛度。

2 程序驗證

根據推導得到的數學模型,采用Fortran語言編程,建立兩種方法的計算程序。本文采用文獻[6，8]提供的參數對程序的正確性進行驗證。

2.1 國枝方法驗證

圖3為基于國枝方法編程計算得到的車速與臨界傾覆風速之間的關系。已知車輛自重20 t,輪軌接觸點中心跨距為1.5 m,其余參數詳見文獻[6]。從圖3中可知,本文計算結果與文獻計算結果完全吻合。

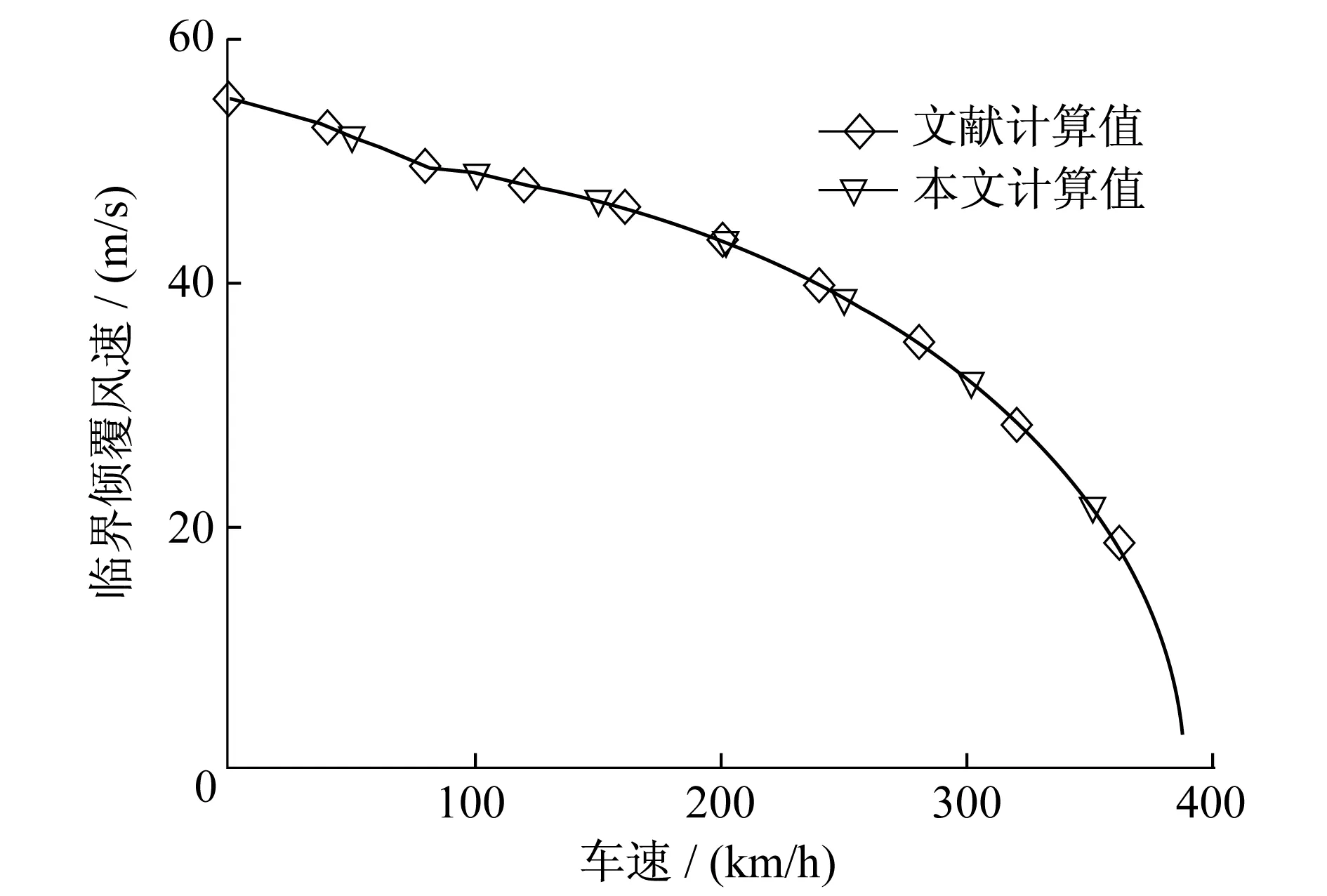
圖3 車速和臨界風速關系

2.2 日比野有方法驗證

圖4、圖 5對比了基于日比野有方法計算得到的傾覆系數及車體重心橫向位移與文獻試驗及計算的結果。計算所需車輛參數見表1[8]。

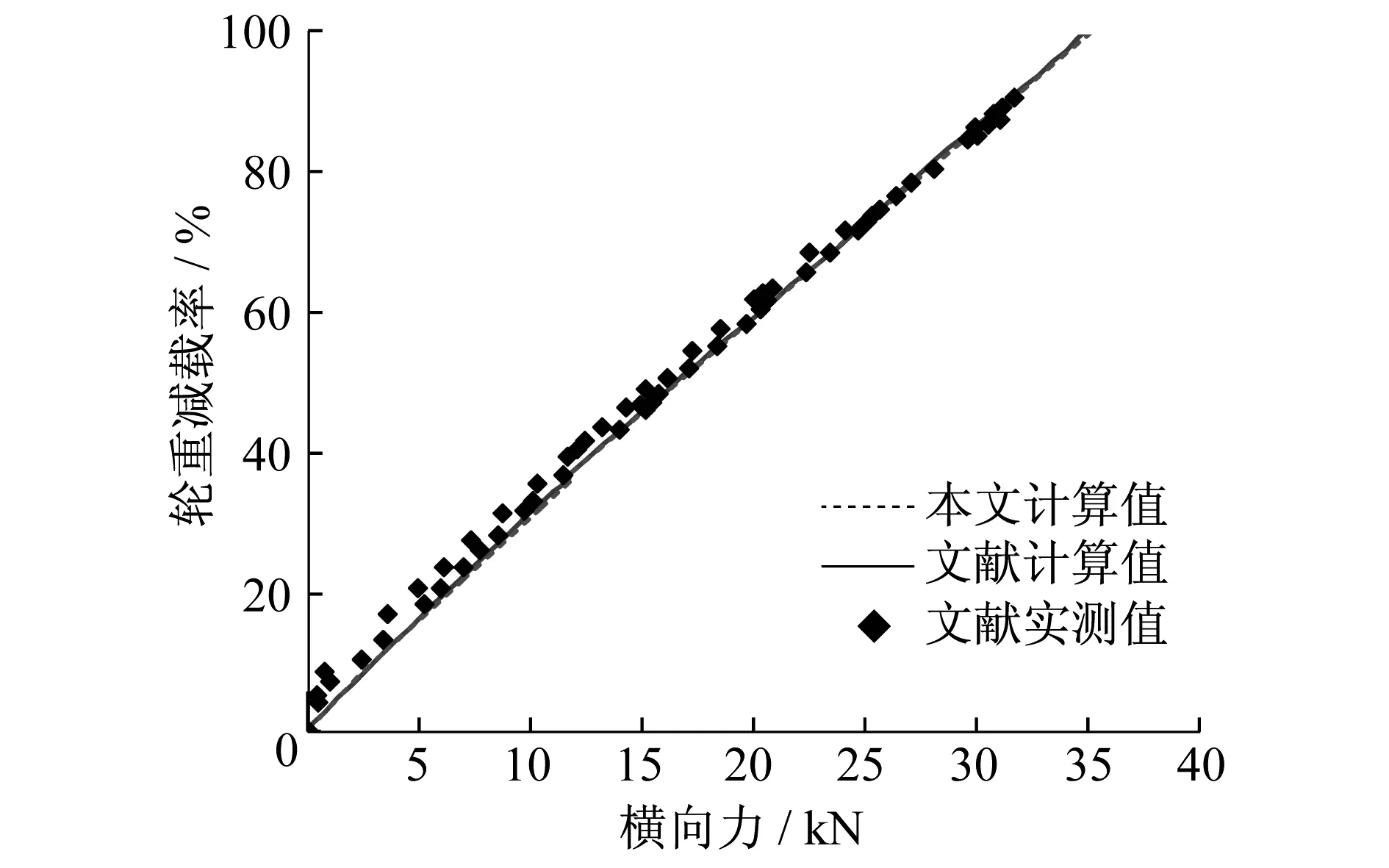
圖4 橫向力和傾覆系數關系

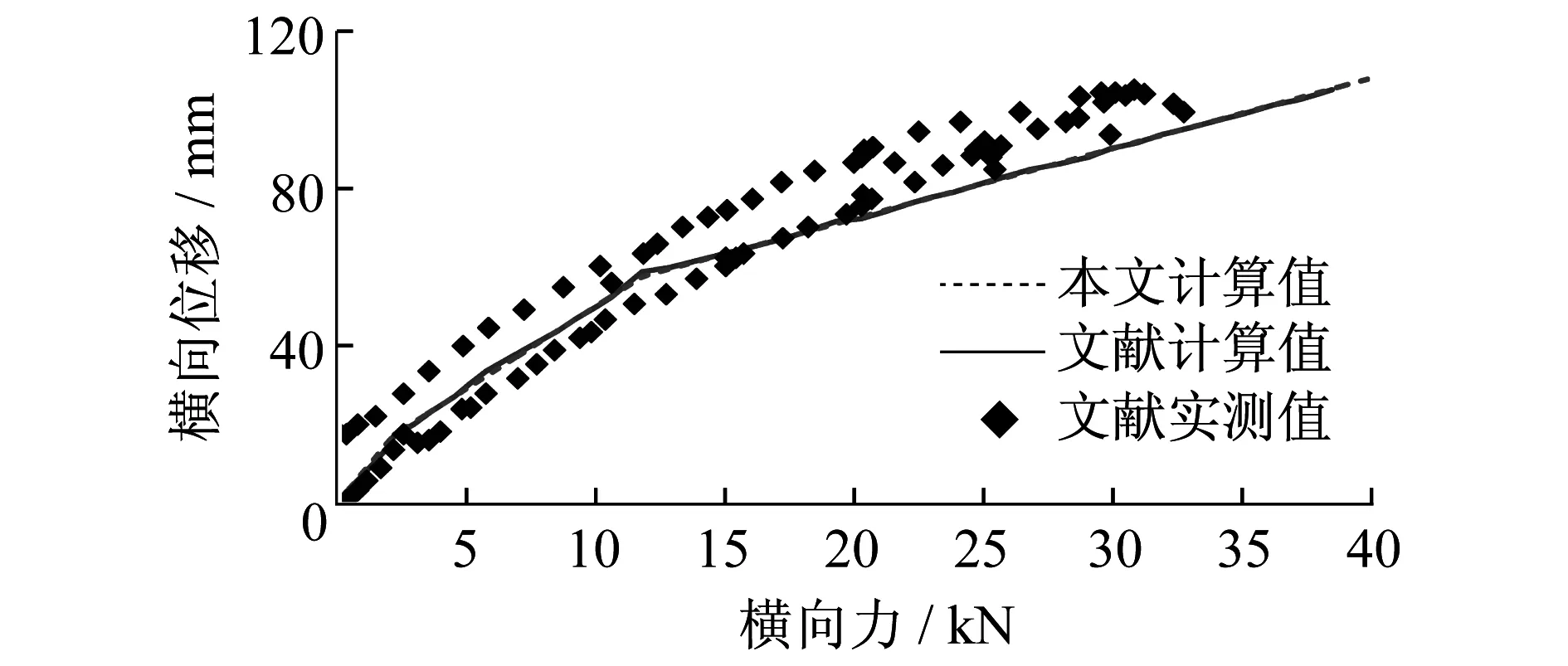
圖5 橫向力和橫向位移關系

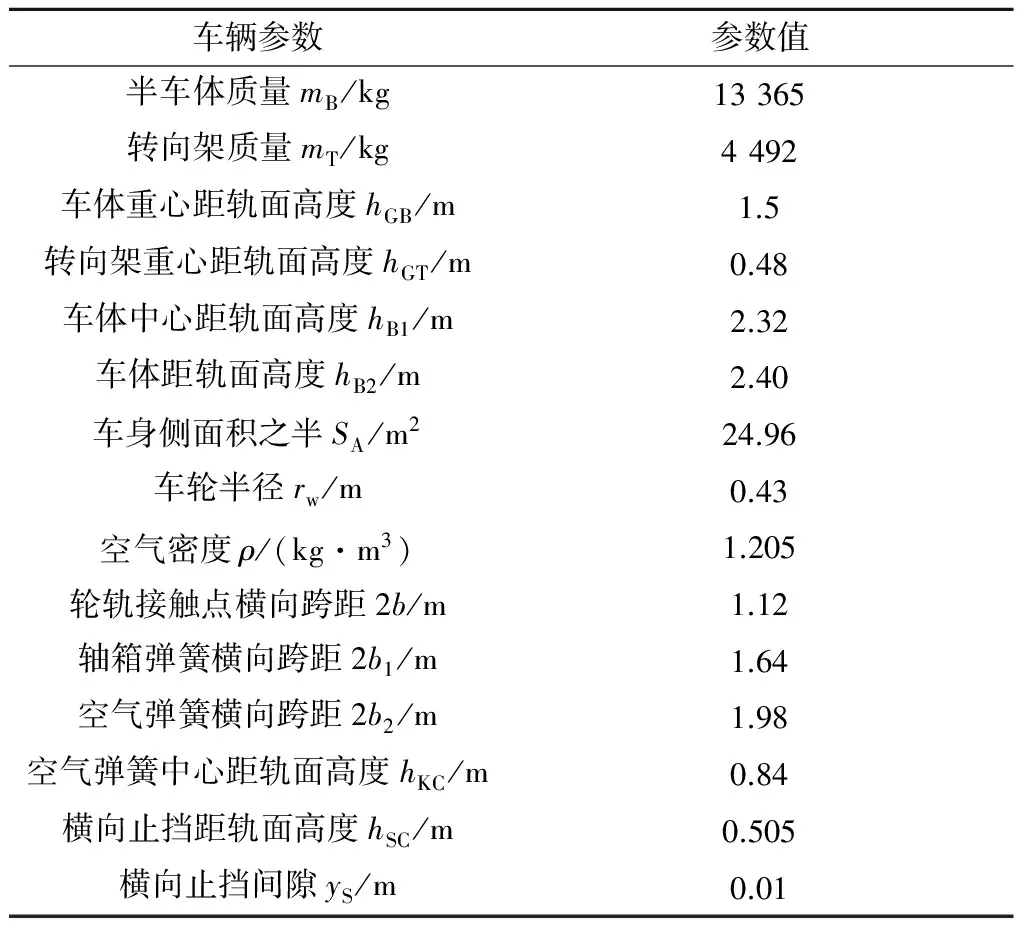
車輛參數參數值半車體質量mB/kg13365轉向架質量mT/kg4492車體重心距軌面高度hGB/m1．5轉向架重心距軌面高度hGT/m0．48車體中心距軌面高度hB1/m2．32車體距軌面高度hB2/m2．40車身側面積之半SA/m224．96車輪半徑rw/m0．43空氣密度ρ/(kg·m3)1．205輪軌接觸點橫向跨距2b/m1．12軸箱彈簧橫向跨距2b1/m1．64空氣彈簧橫向跨距2b2/m1．98空氣彈簧中心距軌面高度hKC/m0．84橫向止擋距軌面高度hSC/m0．505橫向止擋間隙yS/m0．01

圖4計算結果與文獻[8]計算所得結果完全吻合,準確反映了試驗結果。圖 5計算結果與文獻計算結果完全吻合。文獻[8]分析了造成計算結果與試驗結果差異變大的原因在于車體側滾時先后碰到橫向止擋和垂向止擋后,車體重心的實際位移和計算的位移不一致。

2.3 國枝方法和日比野有方法對比

當橫向力線性增大時,分別以上述兩種方法計算車輛傾覆系數,結果如圖 6所示。可以看到,相同的橫向力作用下,國枝方法計算所得傾覆系數小于日比野有方法。該結論與國外試驗結果相同[16]。造成這種結果的原因在于:①國枝方法沒有考慮氣動升力;②國枝方法只考慮了橫向和垂向剛度對車輛傾覆的影響,但沒有考慮互相的影響;③該方法沒有考慮止擋對車輛傾覆的影響。

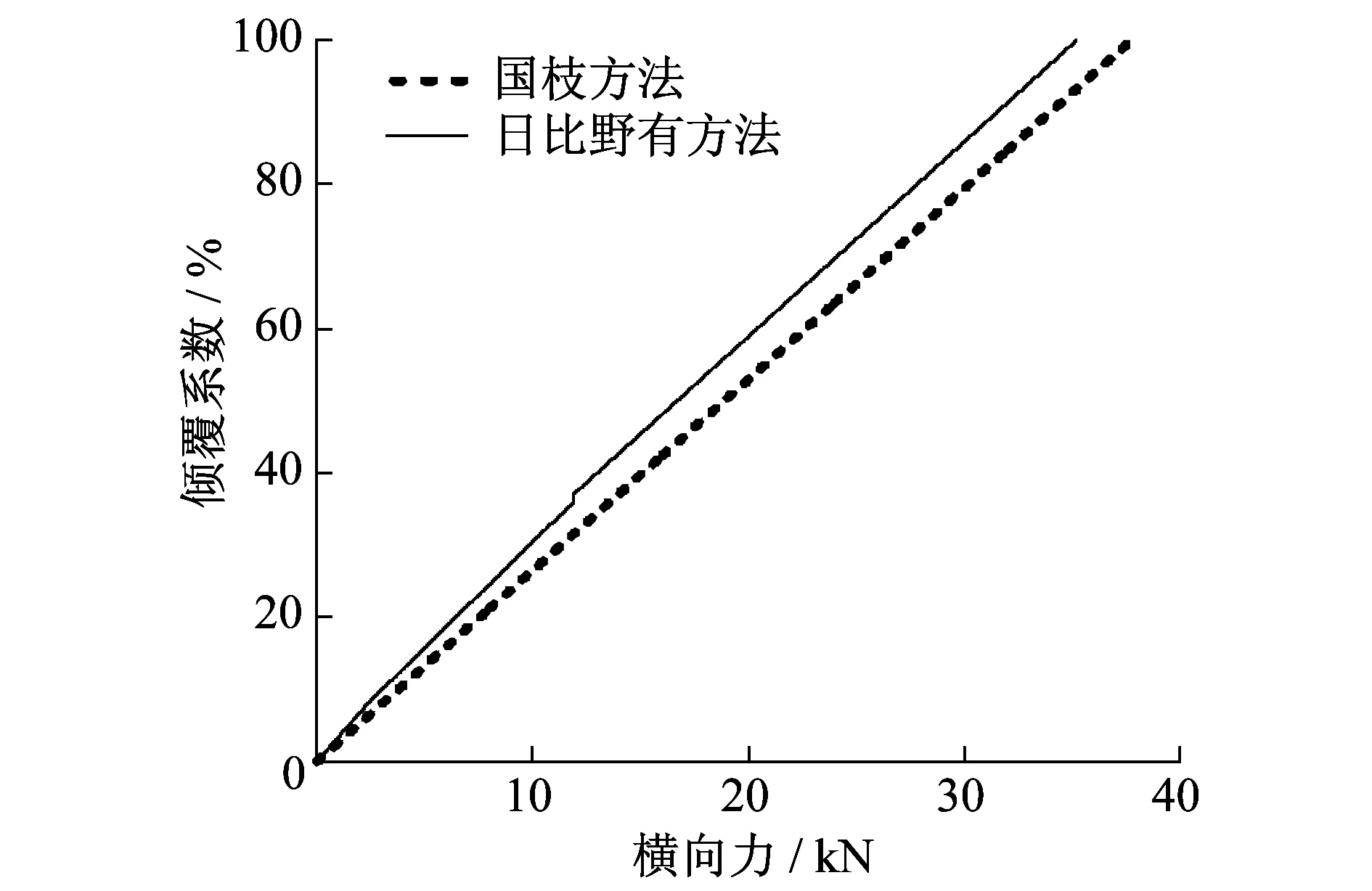
圖6 橫向力和傾覆系數的關系

3 影響車輛傾覆系數的因素分析

對影響車輛傾覆的多個因素進行數值模擬。

3.1 車體自重對傾覆系數的影響

從已掌握的資料看,高速列車的車體自重范圍在26～52 t之間。改變車體自重,計算其傾覆系數。傾覆系數與車體自重變化的關系如圖7所示。其中,橫坐標為CRH2車體自重與CRH5H車體自重的比值。參考研究團隊針對蘭新高鐵第二雙線進行的CFD(Computational Fluid Dynamics)數值模擬結果及其他文獻,列車以250 km/h通過風區時受到的橫向力在25 kN左右。

圖7 車體自重對傾覆系數的影響

由圖7可知,相同的橫向力作用下,隨車體自重的增大,傾覆系數逐漸變小,橫風下安全性增強。這與一般的認識相同。可見,在目前車體輕量化趨勢下,需從車體懸掛剛度及減小橫向力等方面入手,減小輕量化車體引起的抗傾覆性能惡化的趨勢。

3.2 懸掛剛度對傾覆系數的影響

圖8所示為抗側滾扭桿剛度、一系懸掛剛度及二系懸掛剛度與傾覆系數的關系。其中橫坐標為計算時CRH2各懸掛部件剛度與CRH5H各部件剛度的比值。可以看到,隨抗側滾扭桿、一系懸掛剛度及二系懸掛剛度的增加,傾覆系數均有減小的趨勢。其中抗側滾扭桿剛度與一系懸掛剛度變化對傾覆系數的影響比二系懸掛剛度變化的影響顯著。

圖9所示為橫向止檔剛度對傾覆系數的影響。可見,隨著橫向止檔剛度的增大,車輛的抗傾覆性有所提升。

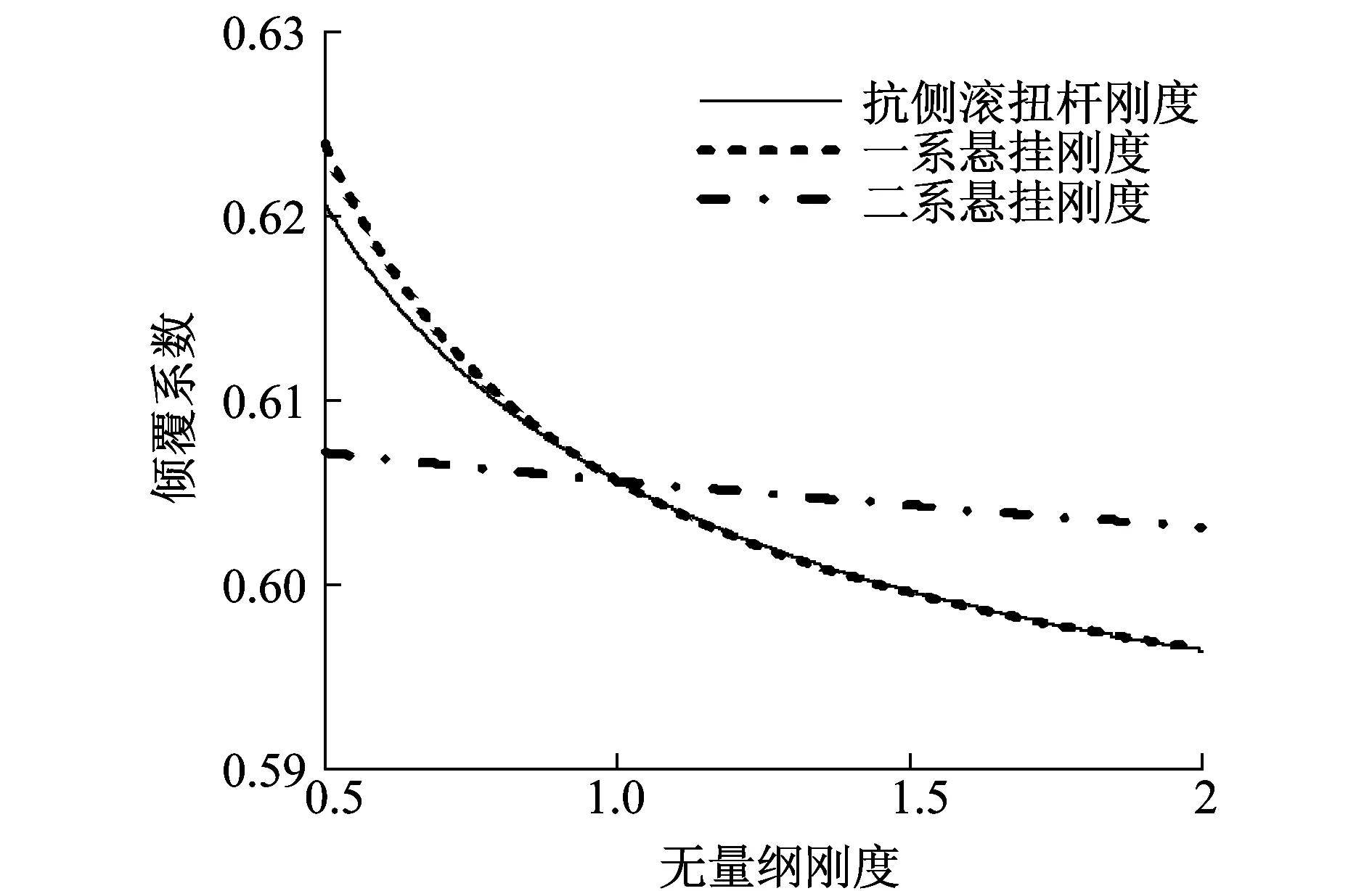
圖8 懸掛部件剛度對傾覆系數的影響

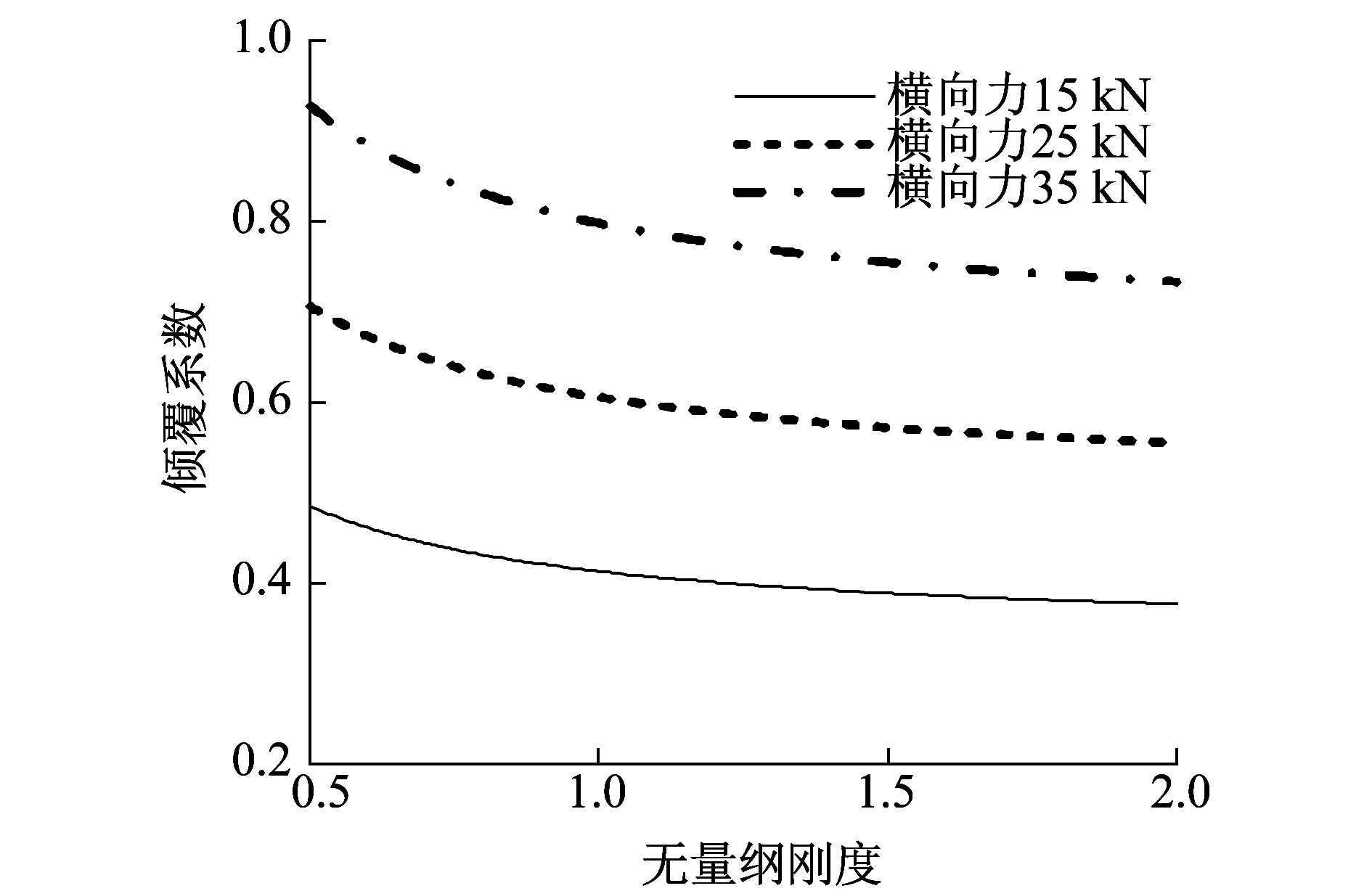
圖9 橫向止檔剛度對傾覆系數的影響

4 結語

國枝方法和日比野有方法都是以靜態力矩平衡為基礎原理,其建模容易,計算時間短。日比野有方法是在國枝方法的基礎上進行修正而來。本文運用靜態方法建立了CRH5H動車組傾覆模型,在驗證程序合理性的基礎上,研究了車體自重、抗側滾扭桿剛度、一系和二系懸掛剛度以及橫向止檔剛度對傾覆系數的影響,數值計算結果符合實際規律。結果表明,車輛自重和車體所受橫向力是影響列車傾覆的最主要因素。由于受到其它如軸重、車體機械強度等方面的制約,需要在高速列車輕量化與傾覆安全性之間找到一個平衡點。通過加設擋風墻等設法降低車體橫向力是目前保證風區列車運營安全的主要方法。調節懸掛系統各部件的剛度對提高列車傾覆安全有一定作用,但數值計算分析發現,其對傾覆系數的影響相比車體自重和橫向力的影響要小。

[1] 張強,楊賢為,張永山,等.京滬沿線強降水頻率及大風頻率分布特征[J].氣象科技, 2003,31(1):45-49.

[2] 馬淑紅,馬志福.瞬時最大風速對京津城際CRH3動車組行車安全影響[J].中國科技信息,2008(21):285-286.

[3] 李鯤.大風區高速鐵路新型防風設施研究[J].中南大學學報(自然科學版),2012,43(2):756-762.

[4] 王爭鳴.蘭新高鐵穿越大風區線路選線及防風措施設計[J].鐵道工程學報,2015(1):1-6.

[5] 錢征宇.西北地區鐵路大風災害及其防治對策[J].中國鐵路,2009(3):1-4.

[6] KUNIEDA M.Theoretical Study on the Mechanics of Overturn of Railway Rolling stock[J].Railway Technical Research Report,1972(793):1-15.

[7] ISHIDA Y H H.Static analysis on railway vehicle overturning under vrosswind[J].Railway Technical Research Report,2003,17(4):39-45.

[8] HIBINO Y,Shimomura T,Tanifuji K.Verification of Static Analysis on Railway Vehicle Overturning under Crosswind[J].Transactions of the Japan Society of Mechanical Engineers C,2009,75(758):2605-2612.

[9] 高廣軍.強側風作用下列車運行安全性研究[D]. 長沙:中南大學,2008.

[10] THOMAS D,DIEDRCHS B,Berg M,et al.Dynamics of a High-speed Rail Vehicle Negotiating Curves at Unsteady Crosswind[C]∥Proceedings of the Institution of Mechanical Engineers.London:SAGE Publications Ltd.,2010:567-579.

[11] TAKAHIRO HOSOI K T.Effect of Crosswind on Derailment of Railway Vehicles Running on Curved Track at Low Speed[J].International Journal of Railway,2012,5(2):93-101.

[12] 郗艷紅.橫風作用下的高速列車氣動特性及運行安全性研究[D]. 北京:北京交通大學,2012.

[13] DIEDRICHS B,Ekequist M,Stichel S,et al.Quasi-static modelling of wheel-rail reactions due to crosswind effects for various types of high-speed rolling stock [C]∥Proceedings of the Institution of Mechanical Engineers.London:SAGE Publications Ltd.,2004:133-148.

[14] 王峰,張籍弟.淺談高寒抗風沙動車組設計開發[J].山東工業技術,2015(1):56.

[15] 王福天.車輛動力學[M].北京:中國鐵道出版社,1981.

[16] MORIYAMA A.Verification of railway vehicle overturning under crosswind by field data(an effect of the cross-sectional shape of vehicles)[J].Transactions of the Japan Society of Mechanical Engineers Series A,2012,78(791):2536-2548.

Influencing Factors on Overturning Resistance on High-speed Railway Vehicles against Crosswind Based on Static Method

LUO Lulin, CHU Qixing, JIA Yongxing, NIU Jun, MEI Yuangui

With the rapid development, more high-speed railways are constructed in strong wind regions, so the overturning resistance of railway vehicles against crosswind should be studied. Two different methods, KUNIEDA's method and Yu HIBINO's method are compared, which are used to evaluate the overturning stability of railway vehicles. An overturning resistance model is established based on the CRH5H EMU, the effect of different parameters, such as dead weight, bogie frame I and the hanging stiffness of bogie frame II against overturning is studied. The calculation results are in accordance with the order of nature. The numerical model and method can be used in the safety design of railway vehicle running in strong wind regions.

high-speed train; overturning stability; static method

*中國鐵路總公司科研試驗(Z2014-034);甘肅省高等學校基本科研業務費項目(214145)

U 271.91.1

10.16037/j.1007-869x.2017.01.005

2015-05-26)