淺析幾何法在曲柄滑塊式襟翼機構設計中的應用

董 萌

（中國商飛上海飛機設計研究院，上海201210）

為使襟翼在飛機起飛、巡航、著陸過程中，處于氣動要求的指定位置，飛機襟翼的驅動機構設計型式有多種多樣，其中曲柄滑塊式機構是應用非常廣泛的一種（見圖1）。該型機構工作原理為：驅動器驅動搖臂轉動，使滑塊在滑軌上移動，襟翼與連桿固定在一起，隨著滑塊的移動，襟翼變換位置，滿足氣動設計要求。

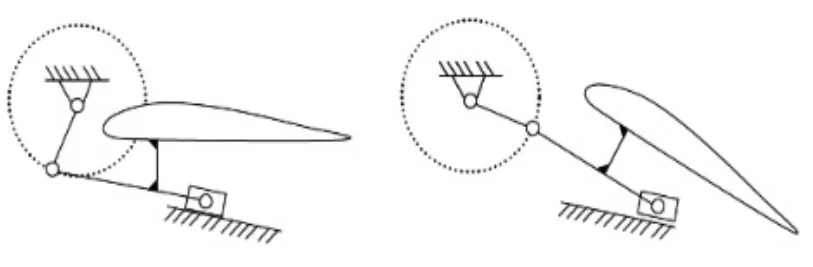
圖1 曲柄滑塊式襟翼機構

在民用飛機后緣襟翼機構設計中，往往已知飛機在起飛、巡航、著陸過程中各工況下的襟翼位置，本文以曲柄滑塊機構襟翼機構為例（見圖1），介紹幾何法在襟翼機構設計、確定襟翼位置中的應用。

1 幾何法原理[1]

曲柄滑塊機構OAC（見圖2）中，連桿AC從位置A1C1到A2C2所轉過的角度為θ，作A1A2和C1C2的垂直平分線na和nc，其交點P12為連桿相對機架從位置1轉到位置2的轉動極點。因ΔP12A1C1≌ ΔP12A2C2，故

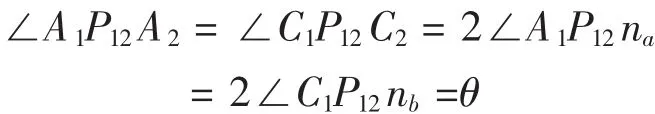
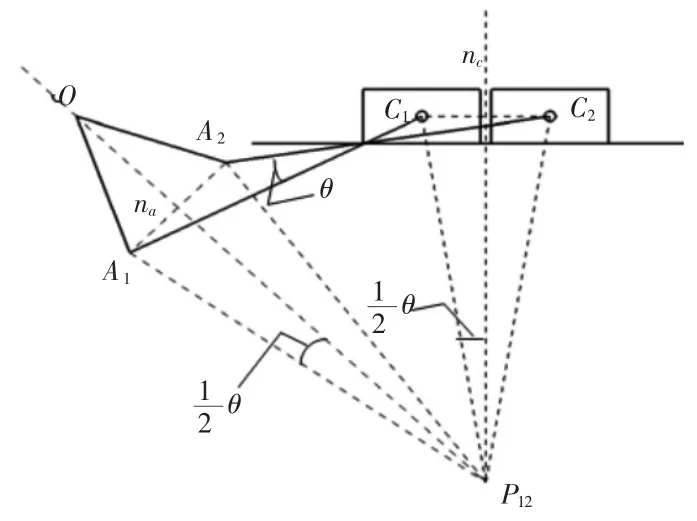
圖2 曲柄滑塊機構

基于上述關系，推論如下：

1）連桿AC（襟翼）上任意點均繞P12做定軸轉動，且P12點唯一；

2）曲柄與連桿鉸鏈點A1在與na夾角為的直線上；

3）連桿與滑塊鉸鏈點C1在與nc夾角為的直線上；

4）固定鉸鏈點O在na上；

5）滑軌平行于 C1C2，且垂直于 nc；

6）鉸鏈點A的位置1和位置2關于na對稱；

7）鉸鏈點C的位置1和位置2關于nc對稱。

2 幾何法求解曲柄滑塊式襟翼機構

在曲柄滑塊襟翼機構設計時，一般地以襟翼起飛、巡航、著陸時的姿態(tài)為輸入。即已知三個連桿位置且連桿鉸鏈點位置未知的情況，幾何作圖法求解機構過程如下，相關字符意義參考圖3.

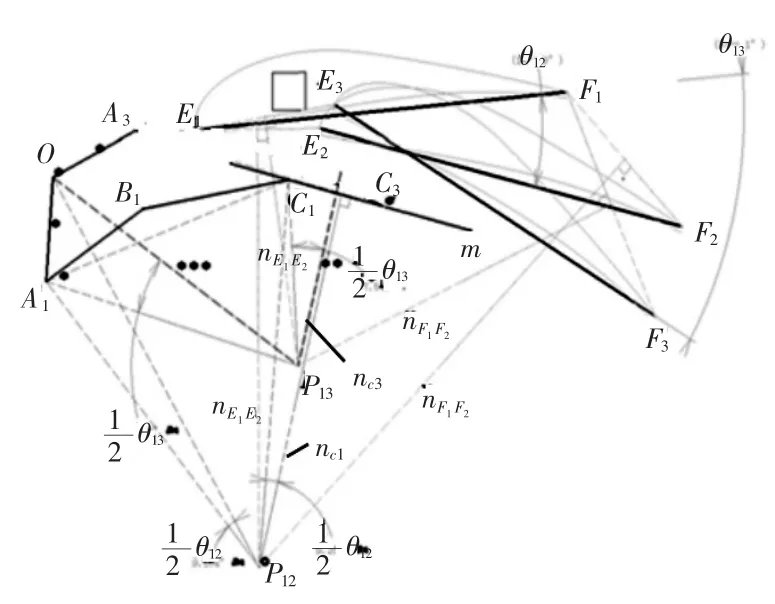
圖3 幾何作圖法求解曲柄滑塊機構

（1）用襟翼截面的翼弦表示襟翼在巡航、起飛、著陸時的位置，分別為E1F1、E2F2、E3F3各位置相對巡航時的轉角為 θ12、θ13；

（2）連接F1F2并作其垂直平分線nF1F2，連接E1E2并作其垂直平分線nE1E2，nF1F2和nE1E2的交點即為轉動極P12，作∠OP12A1=∠n P12C1=θ12；連接 F1F3并c1作其垂直平分線nF1F3，連接E1E3并作其垂直平分線nE1E3，nF1F3和 nE1E3的交點即為轉動極 P13，作∠OP13A2=∠n P13C2=θ13；

（3）固定鉸鏈點O即為la1、la2的交點，連桿鉸鏈點 B 即為 lb1、lb2的交點，滑塊鉸鏈點 C 即為 lc1、lc2、的交點，約束nc1、nc3相互平行，過C作ld1的垂線m即為滑塊的運動直線；

（4）在襟翼運動平面內新建草圖，創(chuàng)建位置1的點O、A、C、直線m、EF的投影并隔離，固定點O和直線m，創(chuàng)建OA和AC的長度約束，創(chuàng)建點C和直線m的相合約束，固連AC和EF，轉動OA，檢驗EF是否滿足巡航、起飛、著陸時的位置要求。

3 應用分析

民用飛機機翼多為后掠機翼，襟翼沿后梁布置，且后梁與機翼展向夾角較大，一般大于20°.當襟翼運動方向與后梁平面垂直時，襟翼運動為簡單的平面運動，上述方法求解的機構優(yōu)化后可直接使用。當襟翼要求與展向垂直的方向（即順氣流方向）運動時，因機翼后梁平面與運動平面存在不再垂直，襟翼的運動不再是平面運動，而是復雜的空間轉動和平動的疊加，上述方法確定機構，僅可滿足襟翼在順氣流平面內的位置要求，不能準確定位襟翼沿機翼展向的運動。

4 結束語

幾何法建立襟翼運動機構的線架模型，快捷并直觀，可清晰反映各鉸鏈點的變化規(guī)律。本文以曲柄滑塊機構為例，詳細闡述了幾何法在襟翼機構設計中的應用，并指出：

1）已知襟翼四個位置，則可唯一確定滑塊鉸鏈點C和滑塊的運動直線m的位置，固定鉸鏈點A和桿鉸鏈點B的位置不唯一，可結合空間及載荷傳遞要求進一步優(yōu)化；

2）該方法適用于機構運動平面垂直于機翼后梁的情況，不完全適用于襟翼順氣流運動的情況，針對順氣流運動的襟翼機構需開展進一步深入研究。

[1]成大先.機械設計手冊·單行本·機構[M].北京：化學工業(yè)出版社，2004.