基于FPGA的流水線單精度浮點數乘法器設計*

彭章國，張征宇,2，王學淵，賴瀚軒，茆 驥

(1. 西南科技大學 信息工程學院，四川 綿陽 621010；2. 中國空氣動力研究與發展中心，四川 綿陽 621000)

基于FPGA的流水線單精度浮點數乘法器設計*

彭章國1，張征宇1,2，王學淵1，賴瀚軒1，茆 驥1

(1. 西南科技大學 信息工程學院，四川 綿陽 621010；2. 中國空氣動力研究與發展中心，四川 綿陽 621000)

針對現有的采用Booth算法與華萊士(Wallace)樹結構設計的浮點乘法器運算速度慢、布局布線復雜等問題，設計了基于FPGA的流水線精度浮點數乘法器。該乘法器采用規則的Vedic算法結構，解決了布局布線復雜的問題；使用超前進位加法器(Carry Look-ahead Adder，CLA)將部分積并行相加，以減少路徑延遲；并通過優化的4級流水線結構處理，在Xilinx?ISE 14.7軟件開發平臺上通過了編譯、綜合及仿真驗證。結果證明，在相同的硬件條件下，本文所設計的浮點乘法器與基4-Booth算法浮點乘法器消耗時鐘數的比值約為兩者消耗硬件資源比值的1.56倍。

浮點乘法器;超前進位加法器;華萊士樹;流水線結構;Vedic算法;Booth算法

0 引言

陣列乘法器是采用移位與求和的算法而設計的一種乘法器[1]。陣列乘法器具有規則的結構，易于布局布線等特點。隨著乘數位寬的增加，部分乘積的個數也成倍地增加，部分乘積項數目決定了求和運算的次數，直接影響乘法器的速度。修正的Booth算法對乘數重新編碼，可以減少相加的部分乘積的數量，因為部分積的存在，部分積相加過程與陣列乘法器沒有太大差異。為了實現速度的提高，Wallace樹結構可以改變部分積求和方式，將求和級數從O(N)減少到O(logN)。因此現有很多乘法器設計都采用修正的Booth算法與Wallace樹結構相結合的方法。但是Wallace樹結構缺乏規整性，布局布線困難；引線的延長導致寄生電容增加，妨礙了電路速度的進一步提高。同時不規則的結構會增加硅板的面積，并且由于路由復雜而導致中間連接過程的增多，繼而導致功耗的增大[2-3]。

吠陀乘法器具有其獨特規則的結構，隨著乘數位寬的增加，門延遲和面積的增加很緩慢，因此乘法器能夠在時間延遲、面積、功耗上達到最優。文獻[4]設計了一種高速的4×4位吠陀乘法器，通過實驗證明了4×4位吠陀乘法器比同位寬的陣列乘法器、Booth算法乘法器的運算速度快；文獻[5]設計了單精度的浮點乘法器，其中尾數計算部分分別采用了吠陀乘法器和Booth算法乘法器兩種方法，結果證明吠陀乘法器在時間延遲和面積上都優于Booth算法乘法器；文獻[6]在吠陀乘法器中分別采用行波進位加法器(eRipple Carry Adders，RCA)和超前進位加法器(eCarry Look-ahead Adder，CLA)計算部分乘積的和，通過實驗數據對比，采用超前進位加法器可以獲得更高的速度和占更少的面積。然而對于海量的圖像數據進行浮點數乘法運算時，每一組數據從運算開始到結束期間會產生時間延遲，可以在乘法器中加入流水線結構來減少延遲時間，為此本文設計了一種基于吠陀數學的流水線浮點乘法器。

1 總體設計

本文所設計的單精度浮點數乘法器主要包含以下幾個部分：24位吠陀乘法器、一個8位無符號加法器、一個9位無符號減法器、一個符號位計算單元和一個標準化單元。其結構框圖如圖1所示。

圖1 單精度浮點數乘法器結構圖

1.1 符號位與階碼計算

IEEE 754標準[7]為二進制浮點運算提供了一個精確的浮點數格式計算規范操作及異常處理。這一標準定義了32位單精度浮點數和64位雙精度浮點數兩種類型。它們都分別由符號位、尾數、階碼組成，表1給出了單精度浮點數格式，由式(1)表示為：

P=(-1)S2(Exp-Bias)M

第三，高校要利用“互聯網+監管”的方式來營造良好的網絡環境。“互聯網+”時代的到來拓展了大學生企業家精神教育的新內容，形成了開放、互通、共享的教學模式，同時還實現了從大一統教學到個性化教學的轉變，大學生實現了從被動學習到主動學習的轉變。但是龐大冗雜的信息、開放自由的環境也給正處于成長期的大學生提供了負面信息傳播和宣泄的場所，高校要實時對互聯網中良莠不齊的信息進行篩選與甄別，及時關注學生的思想形態，營造風清氣正、積極向上的網絡環境。

(1)

式中S代表符號位；Exp表示階碼；Bias為固定值，其值為127；M為尾數。

表1 單精度浮點數的格式

(1)符號位計算：兩個數相乘的結果的符號位由這兩個乘數的符號位相異或(⊕)得到，如式(2)所示。

S=S1⊕S2

(2)

式中S1、S2為兩個單精度度浮點數的符號位，S為兩者之間的異或結果。

(2)階碼計算：該加法器模塊主要將兩個乘數的階碼相加，其結果再減去偏差值而得到相乘后結果的階碼，如式(3)所示。

PExp=AExp+BExp-Bias

(3)

式中AExp、BExp為兩個單精度浮點數的階碼；Bias為固定值，其值為127。

1.2 24位吠陀乘法器的邏輯電路設計

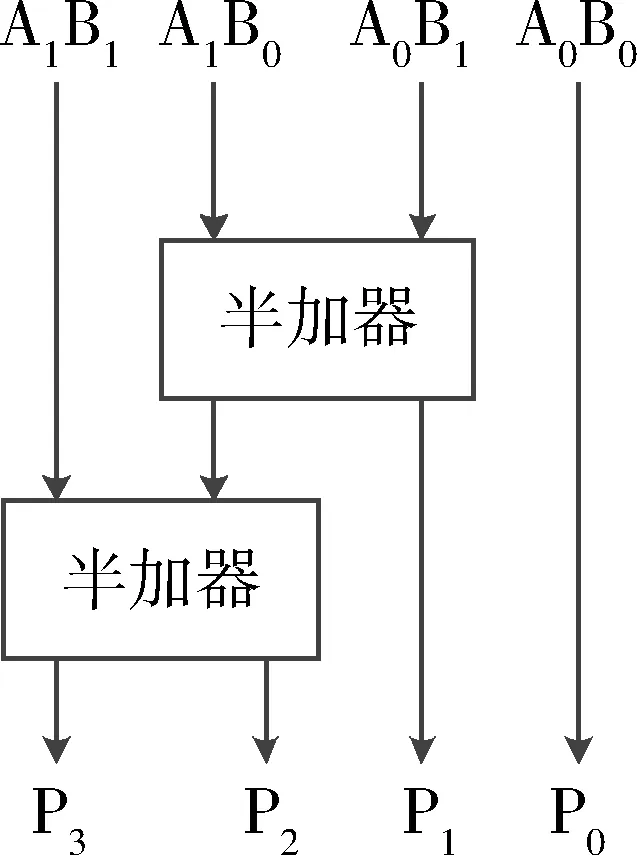
圖2 2×2吠陀乘法器

吠陀乘法器是基于吠陀數學而設計的。吠陀數學是Sri Bharati Krishna Tirthaji(巴拉蒂·克里希納·第勒塔季)在研究印度古代吠陀經文的基礎上重構的數學計算體系，其中包括了算術、代數、幾何、三角函數和微積分等學科的處理方法。本文設計的24位吠陀乘法器是基于Urdhva Tiryakbhyam Sutra(字面意思是垂直和橫向)而設計的，2位吠陀乘法器的結構框圖如圖2所示，它由4個與門和2個半加器組成，它是24位吠陀乘法器的基本組成單元。

根據2位吠陀乘法器的結構，一個4位吠陀乘法器可以分解為4個2位吠陀乘法器和3個4位加法器，如圖3所示。

圖3 4×4位吠陀乘法器

同理，一個8位吠陀乘法器可以由4個4位吠陀乘法器和3個8位加法器組成，因此，n位的吠陀乘法器能夠使用4個n/2位吠陀乘法器和3個n位的加法器實現。綜上，n位的吠陀乘法器被分解成n/2個n/2位的乘法器，然后這些較小位寬的乘法器(n/2位)再次分為更小位寬的乘法器(n/4位)，直到被乘數位寬為2位，從而簡化整個增殖過程。

由吠陀乘法器的結構可知，乘法器中會用到進位加法器將各部分積并行相加，隨著加法器的引入，必然會產生路徑時間延遲，從而降低乘法器的運算速度。本文使用CLA先行求得多位加法各位間的進位值，它由進位位產生進位，各進位彼此獨立，不依賴于進位傳播，從而減少等待進位所需要的時間延遲。其推導過程如下：

設二進制加法器的第i位為Ai和Bi，輸出為Si，進位輸入為Ci，進位輸出為Ci+1，則有：

Si=Ai+Bi+Ci

(4)

Ci+1=Ai&Bi+Ci&(Ai+Bi)

(5)

令：Gi=Ai&Bi，Pi=Ai+Bi，則有：

Ci+1=Gi+Ci&Pi

(6)

只要Gi=1 ，就會產生向Ci+1位的進位，稱Gi為進位產生函數。同樣，只要Pi=1，就會把Ci傳遞到Ci+1位；其中Pi為進位傳遞函數。隨著位數的增加式(5)會加長，但總保持三個邏輯級的深度，因此形成進位的延遲是與位數無關的常數。

24位吠陀乘法器結構圖如圖4所示，其中包括1個16位吠陀乘法器、2個16×8位吠陀乘法器、1個8位吠陀乘法器、3個CLA。

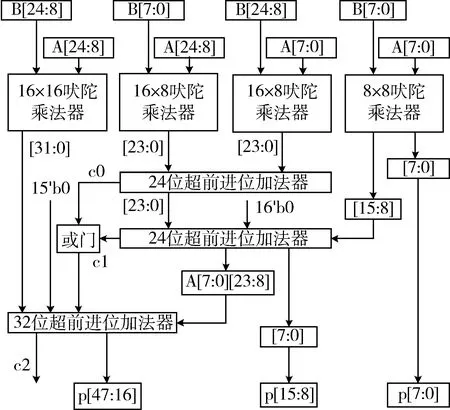
圖4 24位吠陀乘法器結構圖

1.3 流水線結構設計

為了提高FPM對批量數據的運算速度，根據乘法器內部獨特的結構，乘法器中采用了4級流水線進行處理，如圖5所示。通過對24位吠陀乘法器的結構進行分析可知，該乘法器主要由4個不同位寬的吠陀乘法器級聯而成，因此從最基本的2位吠陀乘法器單元出發，在每一個乘法器單元中加入了移位寄存器，形成流水線結構。

2 實驗結果與分析

整個FPM設計使用Verilog HDL語言描述，然后在Xilinx?ISE14.7集成軟件環境下進行了編譯、綜合及功能仿真，最后在XiLinx公司的Virtex-6(xc6vlx240t-1ff1156 )硬件實驗平臺上進行了驗證。FPM中尾數乘積部分是其最重要的部分，因此設計了采用Vedic、基2-Booth、基4-Booth三種算法的24位無符號整數乘法器，并對三種算法的乘法器消耗的硬件資源進行了對比，如表2所示。

由表2可知，由于乘法器中每一級都包含了3個CLA，Vedic算法乘法器消耗的LUTs數目是三種算法乘法器中最多的，而在其他方面的資源消耗是最少的。基4-Booth算法乘法器相對于基2-Booth算法乘法器消耗了更多的資源。三種算法的24位無符號整數乘法器的仿真波形如圖6～圖8所示。其中基2-Booth算法完成一次計算需要52個時鐘周期，基4-Booth算法需要15個時鐘周期，而Vedic算法乘法器由組合邏輯電路設計而成，不需要消耗時鐘周期。

表2 三種算法的24位無符號整數乘法器消耗硬件資源數目對比 (個)

圖6 基2-Booth算法的24位無符號整數乘法器仿真圖

圖7 基4-Booth算法的24位無符號整數乘法器仿真圖

圖9 基2-Booth算法的浮點乘法器仿真圖

圖10 基4-Booth算法的浮點乘法器乘法器仿真圖

圖8 Vedic算法的24位無符號整數乘法器仿真圖

圖11 Vedic算法的浮點乘法器乘法器仿真圖

表3列出了基2-Booth、基4-Booth兩種算法設計的FPM與本文設計的基于吠陀數學的流水線FPM在消耗FPGA資源數目上的對比。

由表3所知，三種方法的FPM在資源、時鐘周期消耗上與無符號整數乘法器所得結論基本一致。其中基2-Booth算法FPM完成一次計算需要52個時鐘周期，基4-Booth算法需要24個時鐘周期，Vedic算法的浮點乘法器需要9個時鐘周期。綜上，Vedic算法FPM在運算速度上更快，這是因為吠陀乘法器的部分積并行相加的結果，采用高速的超前進位加法器，使得運算速度進一步提升。三種算法的浮點數乘法器的仿真波形如圖9～圖11所示。

表3 三種算法的浮點數乘法器消耗硬件資源數目對比 (個)

通過計算基4-Booth FPM與本文設計的FPM消耗資源、時鐘周期數目的比值發現，本文設計的FPM與基4-Booth算法FPM消耗時鐘數的比值約為兩者消耗FPGA資源比值的1.56倍。

3 結論

本文設計了一種基于吠陀數學的流水線FPM。乘法器采用Vedic算法，并在其結構中采用超前進位保留加法器將產生的部分積結果并行相加，從而減少了電路延遲，4級流水線結構也使得乘法器運算速度進一步得到了提高。相比于華萊士樹算法相結合設計的乘法器，吠陀乘法器具有較規則的結構，容易布局布線。雖然本文設計的浮點乘法器消耗了更多的資源，但是在速度上獲得了提高。

[1] 胡正偉，仲順安． 一種多功能陣列乘法器的設計方法[J]. 計算機工程， 2007, 33(22): 23-25.

[2] 夏煒， 肖鵬． 一種高效雙精度浮點乘法器[J]. 計算機測量與控制，2013, 21(4): 1017-1020.

[3] 李飛雄, 蔣林．一種結構新穎的流水線 Booth 乘法器設計[J]. 電子科技， 2013, 26(8):46-48.

[4] KARTHIK S, UDAYABHAUN P. FPGA implementation of high speed vedic multipliers[C].International Journal of Engineering Research and Technology. ESRSA Publications, 2012, 1(10).

[5] KONERU P, SREENIVASU T, RAMESH A P. Asynchronous single precision floating point multiplier using verilog HDL[J]. IJ of Advanced Research in Electronics and Communication Engineering, 2013.

[6] ANJANA S, PRADEEP C, SAMUEL P. Synthesize of high speed floating-point multipliers based on Vedic mathematics[J]. Procedia Computer Science, 2015, 46: 1294-1302.

[7] IEEE 754-2008, IEEE Standard for Floating-Point Arithmetic[S]. 2008.

彭章國 (1990-)，男，碩士研究生，主要研究方向：數字信號和視頻圖像處理技術。

張征宇 (1971-)，通信作者，男，博士，研究員，主要研究方向：光學測量及其在風洞實驗中的應用等。E-mail：zzyxjd@163.com。

王學淵 (1974-)，男，博士，副教授，主要研究方向：測試數據采集與處理。

A single precision floating-point multiplier design of assembly line based on FPGA

Peng Zhangguo1，Zhang Zhengyu1,2，Wang Xueyuan1，Lai Hanxuan1，Mao Ji1

(1.School of Informatin Engineering, Southwest University of Science and Technology, Mianyang 621010,China;2. China Aerodynamics Research and Development Center, Mianyang 621000,China)

Considering the existing floating-point multiplier based on Booth algorithm and Wallace tree, which has slow speed and complex layout, a single precision floating-point multiplier is designed using Vedic mathematics. The Vedic multiplier(VM) has a regular structure therefore can be easily placed and routd in a silicon chip. Carry look-ahead adder (CLA) structure is used to add the part of the product in parallel for reducing the path delay. The floating-point multiplier design employs an optimized 4-stage pipeline processing and the simulation and synthesis are done in Xilinx?ISE 14.7.The results prove that under the condition of the same hardware, the ratio of consumed clock number between the designed multiplier in this paper and arithmetic point multiplier based on 4-Booth is about 1.56 times than that of consumed hardware resources.

floating-point multiplier; carry look-ahead adder; Wallace tree; pipeline structure; Vedic algorithm; Booth algorithm

國家自然科學基金(51475453)；國家自然科學基金(11472297)

TP331.2

A

10.19358/j.issn.1674- 7720.2017.04.022

彭章國，張征宇，王學淵，等.基于FPGA的流水線單精度浮點數乘法器設計[J].微型機與應用，2017,36(4)：74-77,83.

2016-08-29)