思維拔節:實現數學價值與學力生長融合的紐帶
【摘要】數學學科的核心價值在于發展學生的思維能力,而思維能力是學力的核心成分。思維能力的培養是發掘數學學科價值和發展學生學力融合的紐帶。選擇挑戰性的學習材料、設計參考性的教學問題和組織主體性的探究活動,引領學生的思維拔節,可以讓學生感悟數學學科價值,發展綜合學力,實現生命成長。
【關鍵詞】思維;數學價值;學力;學習材料
【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009(2016)44-0035-02
【作者簡介】沈軍,南京市中華中學附屬小學(南京,210000),一級教師,南京市建鄴區數學學科帶頭人。
在當今社會中,學習能力是學生適應社會發展與實現個體可持續發展的核心素養。其中,思維能力是學生學習能力的核心。從這個角度說,聚焦思維能力培養,實現思維的拔節和學力的提升,自然就成為融合發掘數學學科價值和發展學生學力的紐帶。下面筆者以自主開發的數學綜合實踐課《對稱與等分》的教學為例,談一談思維拔節的有效舉措。
一、精心選擇挑戰性的學習材料——實現思維拔節的前提
學習材料是學生解決數學問題、獲得數學知識、提高數學能力的基本載體,也是學生體驗數學價值,形成正確數學觀的重要資源。學習材料主要包括教材中的課程資源與教材外拓展的課程資源。如果學習材料脫離學生的已有知識經驗,高于普遍學力,學生“跳起來摘不到果子”,缺少成功的體驗,就沒有思維的欲望和思維拔節的可能。因為只有學習材料具有一定的挑戰性,學生的思維才會被激活。這就要求教師在選擇學習材料時,要把它落在學生的“最近發展區”,同時鋪設臺階引領學生拾級而上,這樣才能實現思維的拔節。本節課學習材料設計分為三個層次。
層次一:研究單個基本圖形的對稱與等分。先從圓開始,然后到正方形和長方形,再到平行四邊形。
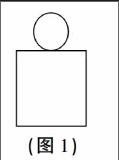
層次二:研究兩個基本圖形組成的組合圖形的對稱與等分。先出示一個圓和一個正方形組成的軸對稱圖形(如圖1)。隨著圓不停地滾動,圓的位置發生了變化,組合圖形也從最初的軸對稱圖形過渡到非軸對稱圖形。最后出示一個圓和一個平行四邊形組成的非軸對稱圖形。
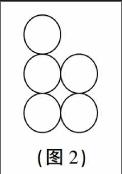
層次三:多個基本圖形組成的組合圖形的對稱與等分。材料中先提供了五個圓組成的軸對稱圖形,然后變化圓的位置,過渡到非軸對稱圖形(如圖2)。
與第一、二層次的材料相比,第三層次的材料更具挑戰性,也更具吸引力。教師沒有繼續安排三個圖形的組合,而是安排了五個圖形的組合。為了使學生“跳一跳能摘到果子”,材料仍然先出現軸對稱組合圖形,再到非軸對稱組合圖形。這樣處理既不高于學生的思維水平,讓學生感覺無從下手,也沒有讓學生的認知停留在低水平上,束縛學生思維的發展。特別是非軸對稱組合圖形,給學生留有一個自由的、廣闊的空間,使學生打破原有的思維方式和習慣,從多角度、多層次來思考問題,拓展了學生思維的廣度與深度。
整節課學習材料的安排遵循從具體到抽象、從簡單到復雜、從低級到高級的兒童認知發展規律。學習材料之間存在一定的內在層次性和關聯性,有助于促進學生對數學知識和數學規律的理解。學生在學習過程中始終有“柳暗花明又一村”的新鮮感,不但學習興趣濃厚,而且思路得到拓寬,思維定勢被打破,實現了從現有發展水平到潛在發展水平的提升。同時,學生不僅實現了思維拔節,還掌握了學習數學的方法。由此可見,學習材料的開發和利用已經成為發展學生思維的先決條件。在需要提供學習材料的課型上,教師選擇材料時應關注這樣幾點:(1)把握學生的原有認知水平,只有貼近學生的學習起點,才能激發學生的學習興趣。(2)選擇有思維含量的學習材料,一節缺乏智力挑戰的數學課,即使課堂氣氛再活躍,也算不上一節好課。只有準確定位學習材料的思維含量,才能激發學生的探究欲望。(3)提供適量的學習材料,不能太多也不能太少,過多會分散學生對關鍵知識點的注意,過少則缺少探究價值。
二、巧妙設計參考性的教學問題——搭建思維拔節的支架
問題是數學的心臟,也是數學思維發展的起點。數學思維的過程就是不斷提出問題和解決問題的過程。一般來說,課堂問題可分為是非性問題、展示性問題和參考性問題,它們的性質各不相同。三類問題對于學生的思維要求逐步提升,而課堂上學生的思維往往就在提出參考性問題之后得到拔節。好的參考性問題是學生從數學活動奔向教學目標之間的思維階梯,是思維拔節的腳手架。因此,教學中我們要深層地思考問題的性質,精心設計問題,為學生搭建導向性支架,引導學生按正確的、有價值的方向拔節。本節課在問題設計上提供了三次支架。
支架一:引導學生從圖形的對稱性想到非對稱性;支架二:引導學生從找出將軸對稱圖形分成面積相等的兩部分的直線,到找出將非軸對稱圖形分成面積相等的兩部分的直線;支架三:引導學生從經過一個中心點把圖形分成面積相等的兩部分,到經過兩個中心點把組合圖形分成面積相等的兩部分。
當然問題源自學習材料,一個好的學習材料再配以深度的問題,學生的潛在能力將得以發掘。整節課中,參考性問題為學生奔向教學目標提供了必要的指引。在問題的引領下,學生開展了有結構、有序的活動。在學生的思維陷入困境時,教師的問題可謂一盞明燈,為更深入地開展數學思維活動提供方向和動力,適時地引領學生實現思維拔節。
三、合理組織主體性的探究活動——催生思維拔節的力量
在當下的課堂中,學生的思維常常被教師束縛,跟著教師跑,沒有時間進行主動思維,思路被牢牢地捆綁在教師的講授上。在此過程中,學生體會不到成功的快樂,長此以往,對教師提出的問題也就不愿意思考了。因此,要讓學生有足夠的時間和空間經歷觀察、實驗、猜測、驗證、推理與交流等數學活動過程。學生只有通過親身驗證,卷入到學習過程中去,才能產生由內而外的學習動力。本節課中層次清晰的數學活動,為學生思維拔節提供了條件。
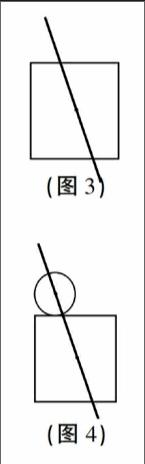
層次一:在研究單個基本圖形時,學生提出猜想:經過正方形的中心點畫出的直線可以將它分成面積相等的兩部分(如圖3)。
層次二:在研究一個圓和一個正方形組成的非軸對稱圖形活動時,學生要驗證經過圓和正方形的中心點畫出的直線能否將組合圖形分成面積相等的兩部分(如圖4)。
層次三:在找出一條直線把五個圓組成的組合圖形分成面積相等的兩部分的活動中,學生把它想象成兩個基本圖形后再畫直線。
兒童的思維是從動作開始的,切斷動作與思維的聯系,思維就不能得到發展(皮亞杰語)。綜觀上述一系列的實踐操作,使學生在不知不覺中經歷了“猜想—驗證—歸納—應用”的過程,有助于積累學生的思維活動經驗。同時,課堂中通過富有挑戰性的活動,有效激發了學生的主動思考,使學生深度參與認知活動,增強了思辨能力,實現了學力提升。
面對充滿無限可能的學生,教師要努力在數學課堂上深入挖掘學科自身的價值,將這種價值轉化為教學行為,最大限度地喚起學生學習的理解力、建構力、思辨力、想象力與創造力。只有把握學科價值和學力生長之間的聯系,找到最佳的生長點,按照學生的思維特點推進教學,才能將學生的學力發掘出來、激勵出來、開發出來。

