“橫向數學化”視角下的教學思辨與效度回歸

臧亞麗+姚建法

【關鍵詞】橫向數學化；教學思辨；效度重構；教學啟示；簡單的周期

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2016）44-0063-02

【作者簡介】1.臧亞麗，江蘇省常州市新北區新華實驗小學（江蘇常州，213127），一級教師；2.姚建法，江蘇省常州市新北區新華實驗小學（江蘇常州，213127）副校長，高級教師，常州市數學學科帶頭人，常州市數學教師基本功競賽一等獎獲得者。

荷蘭數學教育家弗賴登塔爾認為：可以把數學當成一種活動，“數學化”是實施這個活動的方式，也是這個活動的目的。“數學化”可以分為兩類：第一類是“橫向數學化”，注重把生活世界引向數學的符號世界，將現實情境引向數學體系，建立兩者間的聯系；第二類是“縱向數學化”，注重在數學符號的世界里，在數學體系內部，實現抽象符號的生成、變換、重塑與應用。

在教學中，教師往往會為學生創設豐富的生活情境，并從中剝離抽象出數學學習內容，實施從生活到數學的跨越。教師需要思考的是，這種“橫向數學化”的過程是否科學合理，是否符合學情，是否能提高學生正確感知學習內容的效度。下面以蘇教版四上《簡單的周期》一課的教學實踐為例，談談筆者對“橫向數學化”的一些思考，與大家交流和探討。

一、教學嘗試：舍棄教材例圖，使用學生珠串

在三年級上學期，學生已經接觸過圖形規律，探索過“一一間隔排列”的規律，對探索形象直觀的規律積累了一定的經驗。小學生對于珠串手工活動比較感興趣，于是，教師前期布置學生串一串或幾串“你認為具有數學特點的珠串”，發現相當一部分學生根據已有經驗與認識，串出了具有“數學味”的珠串。因此，教師舍棄了教材例題圖，改用學生的珠串作品進行了以下教學嘗試：

1.PPT呈現珠串作品，學生欣賞并交流從中發現的數學現象。

師：下面這兩串珠串（如圖1）的排列有什么共同特點？先獨立觀察，再在小組里說一說。

生1：它們都是重復出現的。

生2：第一幅是藍珠、粉五星、藍珠、綠花，再藍珠、粉五星、藍珠、綠花，再藍珠、粉五星、藍珠……第二幅是黑珠、紫五星、白珠、紫五星，再黑珠、紫五星、白珠、紫五星……

師小結：這兩串珠串都是一組一組重復出現的。（板書：一組一組重復出現）

師：你有什么辦法能讓我們把一組一組看得更清晰嗎？

生3：串珠串的時候把它們一組一組適當分開一些，比如這樣……（該生上臺擺一擺）

生4：在圖上可以畫線隔開。（該生上臺畫一畫）

生5：還可以圈一圈。

師追問：請大家再仔細觀察一下，每一組里面珠串的排列順序是怎樣的？

生6：每一組的排列順序都是相同的。

師提煉并板書：同一事物依次重復出現的現象叫作周期現象。我們今天就一起來學習《簡單的周期》。

2.練習。教師課件展示學生珠串作品的照片（如圖2），讓學生判斷其中的珠串是否具有周期現象，具有周期現象的打“√”，不具有周期現象的打“×”。

實物投影學生作品，重點選擇兩張照片交流：

①為什么這個珠串打“×”？可以怎樣調整使其具有周期性？

②這個珠串打“√”，你能說出其中的周期規律嗎？

3.活動。繼續看圖，圖上的珠串是按照怎樣的順序排列的？用你喜歡的方式記錄下來，可以用語言，也可以用圖形符號。

…………

二、“橫向數學化”視角下的思辨

教師設計珠串這一教學環節，是想引導學生經歷“橫向數學化”的過程，對簡單的周期規律獲得正確的感知。然而，這樣的教學設計真的更貼近學生、更容易讓學生感知其中的周期規律嗎？

從教學反應來看，學生雖然已經能串出具有數學特色的珠串，并能從中發現一些數學規律，但由于珠串形狀繁多（星形、球形、心形等），大小各異，顏色又多種多樣，勢必導致學生觀察它的特征時受到多重無效影響。除此之外，男生對珠串的興趣遠低于女生；有些珠串只有兩三組，組數較少，不利于學生發現規律，而且珠串個數較少，是有限的，不利于學生對個數較多甚至個數無限形成更好的感知。

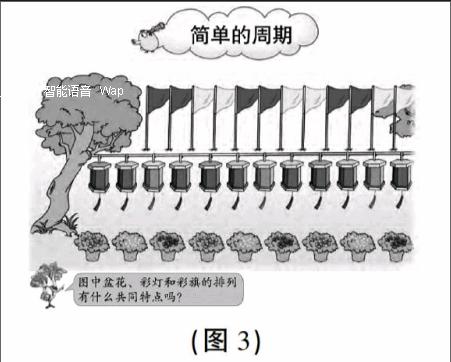
反觀教材呈現的情境圖（如圖3），由近到遠依次是盆花、彩燈、彩旗，它們有規律地擺放著，且從左往右看隱喻著個數的無限或不確定性。擺放的順序（即周期規律）聚焦于顏色，簡潔、清爽、醒目，便于學生看出來，利于學生說出來。教材設問：盆花、彩燈、彩旗的排列有什么共同特點？意在引導學生關注這些物體的排列，尋找它們排列的共同點。學生通過仔細觀察與比較，可以體會到“盆花、彩燈、彩旗的排列都是有規律的”“三種物體都是一組一組地排列的”“同一種物體中，每組的排列完全相同”。學生獲得的這些體會與認知，就是對簡單周期現象的初步感受。

可見，引例素材的選擇，不能只考慮學生的已有經驗，而應圍繞相關學習內容，挖掘其核心的本質要素，為學生的探索作清晰簡明的素材準備。

三、“橫向數學化”的效度重構與教學啟示

教學規律探索課，教師應深入分析教材例題蘊藏的體現教學內容的核心要素，為學生提供合適的引例，給予他們充分的時間與空間，讓他們觀察、交流與討論，逐步明晰引例中隱含的內在規律。如果仍要用珠串作為引例，就要精簡珠串的形與色，或形同色不同，或色同形不同，還要有“無限”的痕跡體現，比如在出示的學生作品圖的后面加上“……”，便于數學化的橫向演進。

另外，筆者注意到，教材中對于“周期現象”的概念揭示，是在學生探究完盆花、彩燈、彩旗的排列規律，并能正確推理出第幾個是哪種顏色之后。“同一事物”“依次重復出現”這些“高效能”的數學化用詞出現略顯滯后，不利于學生表達規律。而上述案例中，教師以珠串作引例揭示數學概念又顯過早，不利于學生充分感知與體驗。因此，可以調整為在學生判斷其他珠串是否也有這種規律后再揭示概念。隨后，可以補充一個教學環節——舉例生活中的周期現象，實現“生活數學化”與“數學生活化”的雙向關聯，使學生更加高效地經歷與體悟“橫向數學化”的過程，也為后面“縱向數學化”的符號化表達與應用提供有力的平臺支撐。

綜上所述，要有效地實現“橫向數學化”，筆者認為，教師應做到以下幾點：一是對選用的例題素材進行篩選與優化，要彰顯教學內容的基本要素；二是合理把握概念揭示的時機；三是注重原生態資源對數學化過程的層次推進；四是關注全體學生的情感調度，讓現實情境適合每一位學生。只有這樣，才能更好地體現教材味、學生味、數學味，提升“橫向數學化”的效度。