混合粒子群OIF—Elman神經網絡系統辨識

黃偉+謝威+付家興

摘 要：本文提出了一種基于混合粒子群優化算法的OIF-Elman遞歸神經網絡辨識方法。混合算法融合了粒子群算法與差分進化算法的優化能力并加入了在群體最優位置附近的高斯變異操作。與三種典型差分進化算法的仿真對比結果說明了，通過以上改進加快了算法的收斂速度，提高了優化精度。將該辨識方法用于實驗室加熱爐換熱器系統雙入雙出耦合對象的辨識中，獲得的對象模型較之標準的Elman神經網絡辨識精度更高，且結果表明本方法與采用反向傳播算法作為學習算法的OIF-Elman模型相比，基于改進粒子群算法優化的模型具有更高的精度和更簡單的網絡結構。

關鍵詞：差分進化；粒子群；高斯變異；OIF-Elman；系統辨識

DOI：10.16640/j.cnki.37-1222/t.2017.05.119

1 概述

神經網絡因具有強大的并行處理能力、自組織和自學習能力、非線性映射能力，在系統辨識領域受到了廣泛的重視[1]。采用神經網絡對系統進行辨識時，無需知道系統的具體結構，通過對相關數據進行訓練可以得到辨識模型的網絡結構，使得辨識更加簡便易行，且可用于閉環辨識。在工程實際中，辨識對象大多為動態系統，且具有較強的非線性，一般的靜態前饋神經網絡雖然可以采用增加外部遲延的方法辨識動態系統，但會使網絡結構復雜化，導致收斂速度變慢。具有內部反饋結構的遞歸神經網絡，因自身具有反饋結構，網絡本身便是一個非線性動態系統，成為辨識動態系統的有效方法之一[2]。本文在OIF-Elman[3]遞歸網絡模型的基礎上，結合改進的粒子群算法對其進行優化，并用于加熱爐換熱器對象的辨識，辨識的結果證實了該方法的可行性和優越性。

2 OIF-ELman神經網絡

2.1 OIF-Elman網絡結構

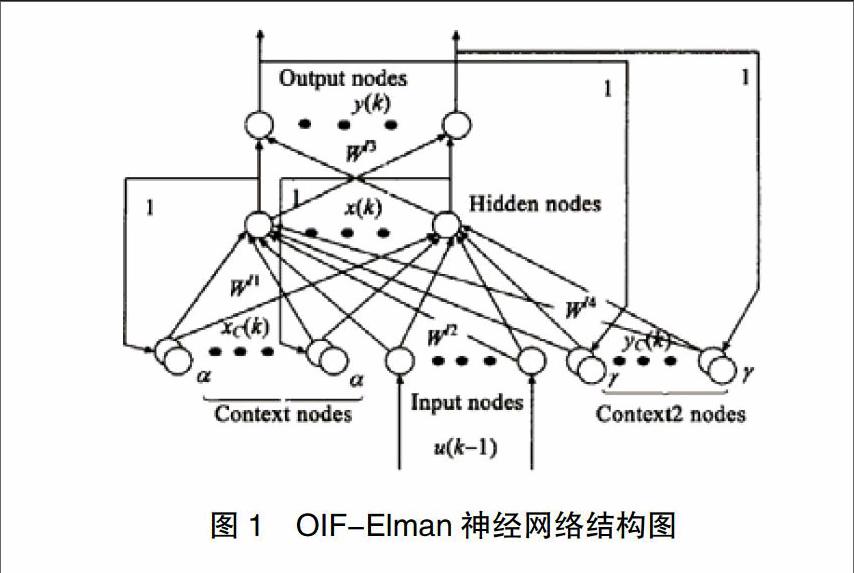
基本的Elman神經網絡在BP神經網絡基礎上加入了局部反饋鏈接和局部遞歸單元，具有了動態系統的結構。OIF-Elman網絡在Elman網絡的基礎上增加了輸出層節點的反饋，強化了對動態系統的擬合能力，被稱為具有輸出-輸入反饋機制的改進Elman網絡[4]。其結構圖如圖1所示，網絡的兩個關聯層的表達式分別為[5]：

，

2.2 OIF-Elman網絡動態系統仿真

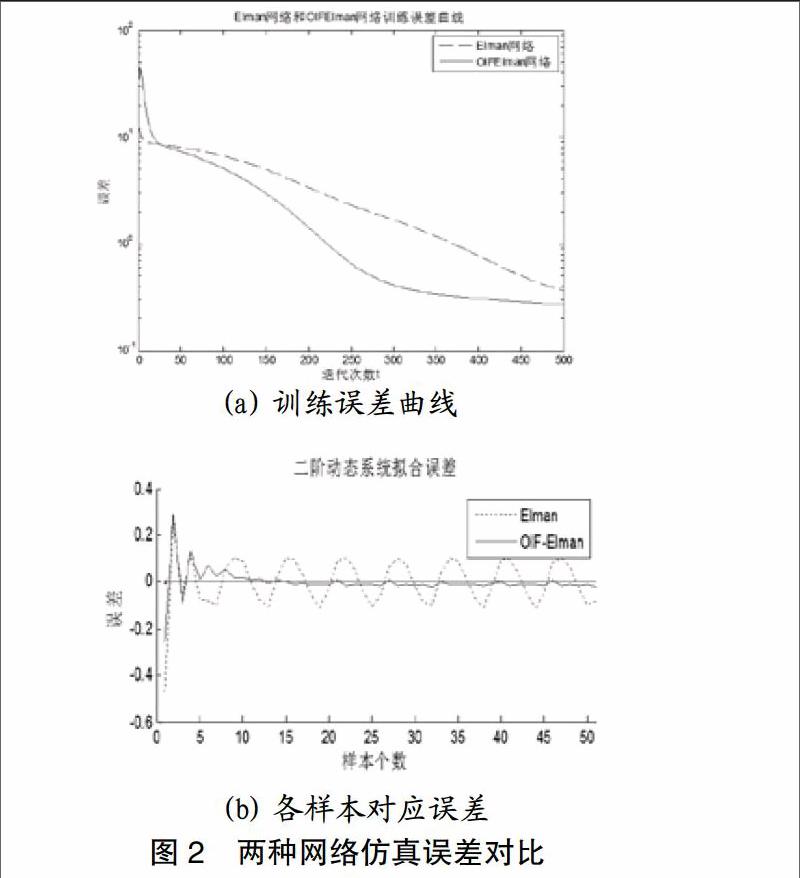
分別采用Elman網絡及OIF-Elman網絡對二階動態系統：，輸入信號為，取樣本個數為50。學習算法均采用誤差反向傳播（BP）學習算法并比較兩種網絡的擬合精度，如圖2所示。圖2（a）為兩種網絡的訓練誤差曲線，圖2（b）為兩種網絡輸出對應每一個樣本的誤差，可見OIF-Elman網絡相比于Elman網絡誤差更小，精度更高，在動態系統辨識上更加有效。

3 混合粒子群優化算法

由于傳統的BP學習算法收斂速度慢易陷入局部最優等缺陷，本文提出一種改進的混合粒子群優化算法作為OIF-Elman神經網絡的學習算法。改進的算法在標準粒子群算法模型的基礎上，融入了高斯變異以及差分進化算法的交叉變異機制，并將本文算法與典型的三種差分進化粒子群算法（DEPSO）在不同目標函數上進行仿真對比。

3.1 算法思想

算法保留了粒子群模型的速度向量，采用常用的一種差分變異策略，增加粒子的多樣性，保證全局搜索能力，但由于目標向量是速度向量，故在此基礎上將基向量改為，并加入基于群體最優的差分向量，加速種群收斂速度，加強了對群體最優附近區域的挖掘能力[6]。文獻[11]中采用了對于最優向量中某一維分量變異的策略得到了很好的效果，在本文算法的高斯變異操作中，只對速度向量的某一維分量進行變異。另外為了進一步加強算法在群體最優附近的挖掘能力，引入高斯變異在最優位置附近進行搜索。有研究指出，全局最優解易出現在粒子群的群體最優位置與個體最優之間[7]，受此啟發，本文算法中取群體歷史最優位置和歷史次優位置之間的區域進行高斯變異。這么選擇首先使高斯變異的范圍根據搜索進程進行變化，搜索前期范圍較大，搜索后期范圍會縮小。其次是因為在算法收斂后期問題的解多在群體最優位置附近，當粒子位置（由于算法的選擇操作，粒子個體最優即是粒子當前位置）未越過最優解時，算法會使粒子向最優解移動并記錄上次最優位置，當粒子由于速度慣性越過最優解時，問題的解便在歷史最優位置和歷史次優位置之間，所以說這個范圍是最具價值的搜索空間。實驗證明這種方式對于單峰及多峰函數起到了局部挖掘，促進收斂的作用。

根據上述原理，本文算法步驟如下：

（1）初始化。初始化種群個數，迭代次數，以及所有粒子的位置和速度。

（2）計算每個粒子的適應度值，初始化種群個體歷史最優和群體最優。

（3）判斷是否達到結束條件，如是則輸出當前全局最優值，否則執行下面步驟。

（4）對粒子速度向量中隨機選擇的一維，按照下面公式進行變異。更新粒子位置后采用差分進化算法的選擇機制，與之前粒子位置的適應度值進行比較，若當前粒子比之前粒子的適應度值更優，則用當前粒子進行替換，否則保留前一代粒子到下一代。

（5）記錄粒子群的歷史最優及歷史次優，采用下式進行高斯變異，在歷史最優與歷史次優之間進行挖掘，尋找更優的粒子對當前最優粒子進行替換，并更新次優粒子位置。

（6）返回步驟（3）。

3.2 數值仿真

將本文提出的算法與標準粒子群算法（PSO）、差分進化算法（DE）以及三種典型的差分進化與粒子群的結合算法[8]（本文將其稱為：I輔助式[9]、II集成式[10]和III協作式[11]）進行對比，選用Ackley多峰函數、Griewank函數、Rastrigin函數、Rosenbrock函數四種測試函數作為算法的目標函數，仿真結果如圖3及表1所示。

由圖3可知，本文改進算法在Rastrigin多峰函數優化上的優勢顯著，PSO算法和DE算法以及類型II均陷入了局部最優，類型I和類型III的改進算法依然繼續搜索趨勢，但與本文所提算法相比速度極慢。在其他函數如Rosenbrock函數仿真結果上，相比于其他算法，本文改進算法達到更高精度，表現出在此單峰問題求解中的優勢。

4 對加熱爐-對流換熱系統辨識

4.1 加熱爐換熱器控制系統的組成

將本文的辨識方法應用到加熱爐換熱器雙入雙出耦合對象，控制系統的方框圖如圖4所示。其輸出為內膽溫度T1和換熱器冷卻水出口溫度T2，輸入為控制器1和控制器2的輸出信號即加熱器與變頻器的開度信號U1和U2。故設計神經網絡辨識模型的輸出為T1和T2，輸入為U1和U2。

訓練樣本以5秒的采樣間隔取控制回路閉合時加入換熱器冷卻水出口溫度設定值后500秒內的100組控制器的輸出以及溫度數據，所有試驗數據做歸一化處理，訓練次數為300次。

4.2 仿真對比及結果分析

將本文方法與采用BP學習的OIF-Elman網絡及采用上述類型III優化算法的OIF-Elman網絡進行對比，如圖5所示。經過訓練，三種網絡模型均收斂到了一定的精度，本文提出的網絡模型相比于BP算法OIF-Elman網絡及類型III-OIFElman網絡以較少的訓練次數收斂到了較高精度。表2為三種模型的辨識誤差，同時也加入了標準Elman神經網絡的辨識誤差作為對比，可以看出采用本文算法的OIF-Elman網絡的辨識精度更高。

圖6為三種網絡模型對訓練樣本輸出信號的擬合曲線，更加直觀地展現出網絡模型的辨識效果，由圖可見，同樣是采用本文算法的OIF-Elman網絡模型相比其他兩種模型對于樣本的擬合效果更好。

5 結束語

加熱爐換熱器對象是一個多入多出的動態過程，采用OIFElman這種遞歸型神經網絡對加熱爐換熱器對象閉環調節過程的實驗數據進行了辨識，得到具有一定精度的神經網絡模型。采用BP算法，網絡的隱層節點較多，收斂速度慢，且精度不高。采用粒子群等智能算法優化神經網絡權值、閾值、關聯系數、關聯層初始值，較之BP算法，智能優化算法表現出了較快的收斂速度與精度，省卻了人為給定關聯系數及關聯層初值這一步驟，同時表現出了較強的搜索能力，簡化神經網絡的復雜性，得出了在同樣規模的神經網絡結構下BP算法無法搜索到的解。本文提出的混合算法較之多種改進的差分進化粒子群算法在仿真結果上表現出較好的搜索能力，并應用到神經網絡對象辨識中，針對加熱爐換熱器對象得到了一種結構簡單，精度更高的神經網絡模型。

參考文獻：

[1]茹菲，李鐵鷹.人工神經網絡系統辨識綜述[J].軟件導刊， 2011，10（03）：134-135.

[2]章國升.基于遞歸神經網絡的非線性系統辨識研究[D].蘭州： 蘭州大學，2010.

[3]時小虎，梁艷春，徐旭.改進的Elman模型與遞歸反傳控制神經網絡[J].軟件學報，2003，14（06）：82-91.

[4]王琛.超超臨界機組非線性動態模型的研究[D].北京：華北電力大學（北京），2010.

[5]姚柳.超超臨界機組的建模與仿真[D].北京：華北電力大學（北京），2011.

[6]宋錦，師玉嬌，高浩等.基于新型變異策略的差分進化算法[J].計算機工程與設計，2016，37（05）：1285-1290.

[7]Gao H，Xu W. Particle Swarm Algorithm with Hybrid Mutation Strategy[J]. Applied Soft Computing， 2011， 11（8）： 5129-5142.

[8]辛斌，陳杰.粒子群優化與差分進化混合算法的綜述與分類[J]. 系統科學與數學，2011，31（9）：1130-1150.

[9]Zhang W，Xie X.Depso：Hybrid Particle Swarm with Differential Evolution Operator[C]//Proceedings of the Ieee International Conference on Systems，man，and Cybernetics， [S.l.]：[s.n.]，2004：3816-3821.

[10]Jun S，Jian L.A Hybrid of Differential Evolution and Particle Swarm Optimization for Global Optimization[C]//Proceedings of the 3rd International Symposium on Intelligent Information Technology Application，[S.l.]：[s.n.]， 2009：138-141.

[11]Niu B，Li L.A Novel Pso-de-based Hybrid Algorithm for Global Optimization[C]//Proceedings of the 4th International Conference on Intelligent Computing，[S.l.]：Springer Berlin Heidelberg，2008：156-163.

作者簡介：黃偉（1966-），女，副教授，研究方向：智能控制、系統辨識、電氣設備狀態檢測與故障診斷。

*為通訊作者