泰森多邊形降雨插值方法在流溪河模型洪水預報中的應用

覃建明，陳洋波，王幻宇

(中山大學地理科學與規劃學院，廣州 510275)

0 前 言

流溪河模型[1,2]是一個精細化的流域洪水預報分布式物理水文模型，其產匯流計算是基于單元網格的，在應用流溪河模型開展流域洪水預報時，需要根據雨量站實測的點降雨，估算各單元上的面雨量。空間插值方法是面雨量估算的主要方法，目前采用的方法主要有泰森多邊形法[3,4]、反距離權重法[5]、克里格法[6]、PRISM法[7]、樣條插值法[8]等，不同的方法有不同的使用條件。

泰森多邊形法[9]是由美國氣候學家A. H. THIESS首先提出的一種根據氣象站的降雨量推求流域面平均雨量的方法。該方法原理簡單而且易于操作，在氣象要素空間插值中得到了廣泛應用。G.Q Tabios等在美國北部地區應用了不同降雨插值方法并對結果進行分析，發現泰森多邊形法和反距離權重法的插值精度相近[10]；徐晶等研究了不同插值方法的優缺點，最后選定泰森多邊形法作為全國七大流域計算面雨量的方法[11]；畢寶貴等在海河流域支流選定了較好地反映實際情況的泰森多邊形法作為面雨量計算方法，對各支流的實況和預報面雨量進行計算[12]；朱求安等在江口流域采用四種插值方法處理降雨數據并輸入新安江模型，發現泰森多邊形法取得較好模擬精度[13]；王國慶等在兩個不同氣候區流域應用水量平衡模型，分析雨量站網密度對月徑流模擬的影響，結果表明雨量站網密度對面平均雨量的計算有一定影響[14]；陽帆等應用四種降雨插值方法在三個小流域進行洪水模擬，發現引入泰森多邊形的距離反比加權法在模型驗證時取得較好精度[15]。

本文的研究目的是探索采用泰森多邊形法，為流溪河模型中小河流洪水預報估算單元網格面雨量的可行性。基于泰森多邊形原理，本文首先提出了基于泰森多邊形法估算流溪河模型單元網格面雨量的方法，針對廣東省中小河流田頭水流域，建立了流溪河模型，優選了模型參數，模擬了六場實測洪水過程，取得了較好的模擬效果，說明泰森多邊形法可以滿足流溪河模型洪水預報降雨估算的需要。分析了雨量站網密度對流溪河模型洪水模擬效果的影響，發現存在臨界雨量站網密度，當雨量站網密度達到臨界值后，利用流溪河模型模擬洪水的變化不大。

1 基于泰森多邊形的流溪河模型網格面雨量估算方法

1.1 泰森多邊形原理

泰森多邊形法又稱垂直平分法或加權平均法[16]。該算法的實質是多邊形區域的降水強度由其包含的一個唯一氣象站降水強度來表示，即將所有相鄰氣象站用直線連接成若干個三角形，并對三角形作垂直平分線，連接這些垂線的交點組成若干個多邊形。將每個多邊形內所包含唯一的氣象站降雨強度代表這個多邊形區域的降雨強度，各個氣象站點降雨強度與其所在多邊形面積權重的乘積之和為流域平均雨量。計算公式為

式中：fi為第i個雨量站所在多邊形的面積，km2；F為流域面積，km2；其余符號意義相同。

該方法原理比較簡單而且容易操作，應用比較廣泛，適用于氣象站空間分布不均勻的地區。當流域內雨量站的數量與位置確定后，泰森多邊形的面積權重保持不變，計算工作量較小。

1.2基于泰森多邊形的流溪河模型網格面雨量估算方法

流溪河模型[1,2]是一個主要用于流域洪水預報的分布式物理水文模型，采用高分辨率的DEM對整個流域進行劃分，從水平方向將流域劃分成一系列的單元，單元的尺度一般較小，是一個精細化的分布式物理水文模型。在單元流域上進行蒸散發量及產流量的計算，各單元上產生的徑流量通過匯流網絡從本單元開始，進行逐單元的匯流，直至流域出口單元。由于流溪河模型的產匯流計算是基于單元層次的，需要根據雨量站的點降雨，估算單元網格上的面雨量。

利用泰森多邊形法估算流溪河模型的網格面雨量的方法是，首先根據雨量站的位置，繪制泰森多邊形，再根據流溪河模型各網格單元中心的坐標，確定該網格屬于哪個泰森多邊形內，以位于該多邊形內的雨量站的降雨作為該網格的面雨量。

2 研究案例與流溪河模型構建

2.1 田頭水流域簡介

田頭水流域[17]位于廣東省北部、湖南省南部，地處廣東與湖南交界處，是北江流域二級支流，流域面積523 km2。田頭水流域屬于山區性河流，洪水陡漲陡落，洪水發生頻繁，是廣東省洪水災害防治的重點流域。圖1為田頭水流域簡圖。

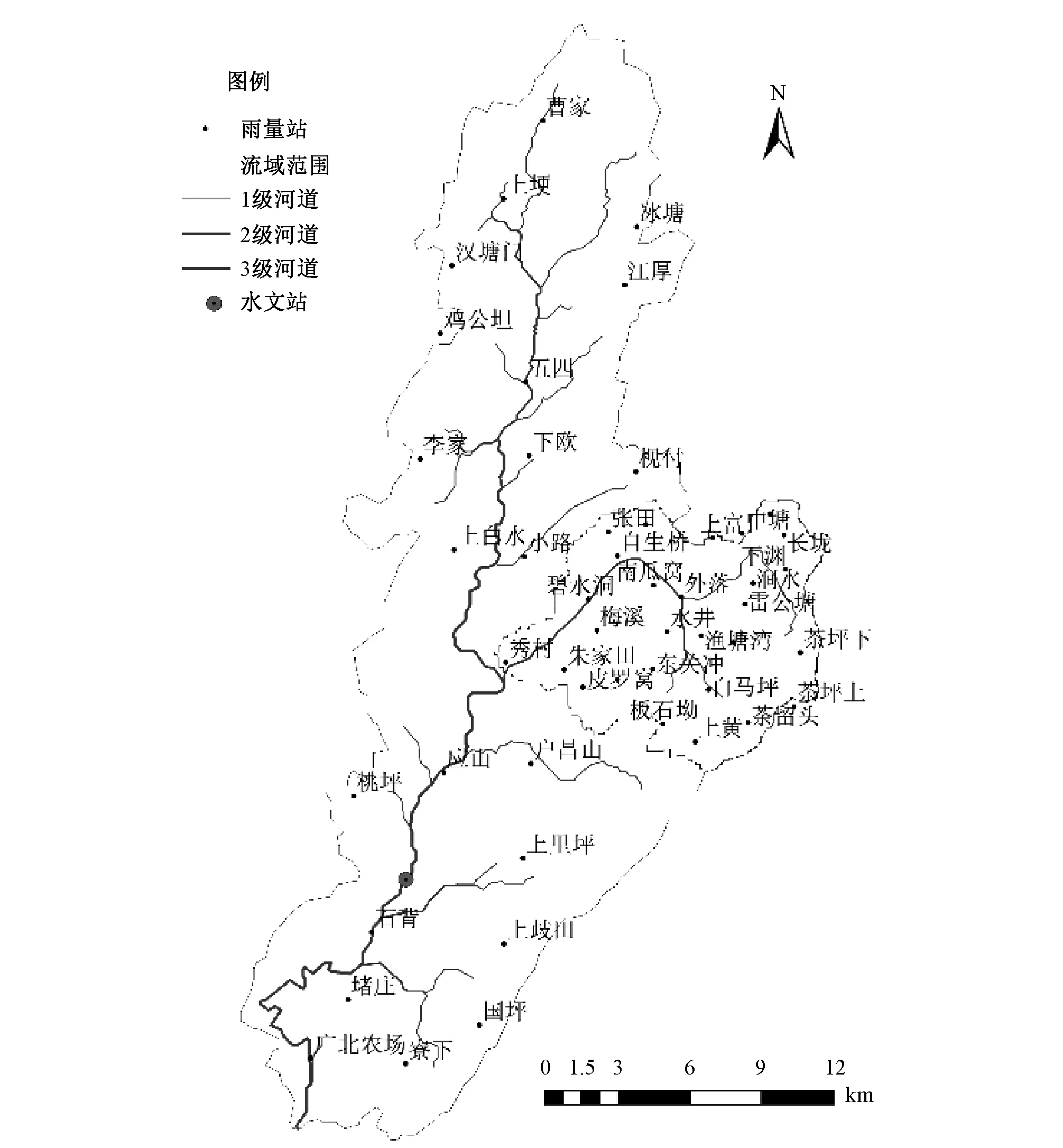
圖1 田頭水流域簡圖Fig.1 The map of Tiantoushui Watershed

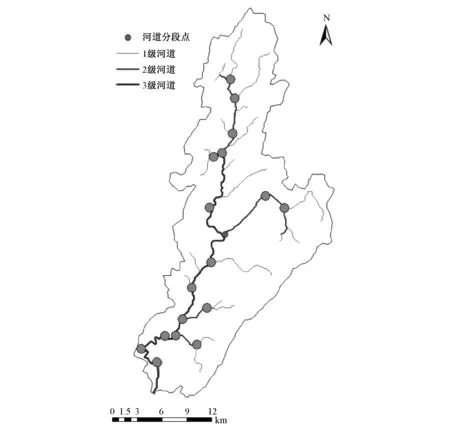
圖2 流溪河模型結構示意圖Fig.2 Structure of Liuxihe Model in Tiantoushui Watershed

田頭水流域內現有50個自動雨量站，其中，一級支流白沙水有30個自動雨量站。田頭水流域下游設有赤溪水文站，控制流域面積442 km2。東沙水流域面積90 km2，是典型的山洪災害易發區。本文研究中，整理出田頭水流域2012年至2015年來觀測到的七場典型洪水過程資料，包括50個雨量站的降雨及赤溪水文站的流量，作為本文的研究數據。

2.2 流溪河模型構建

按照流溪河模型構建方法，采用空間分辨率為90 m×90 m的SRTM數據庫中的DEM對流域進行劃分，將單元分成了河道單元和邊坡單元。由于流域內沒有調蓄能力強的水庫，故未劃分水庫單元。河道劃分為3級河網，參照Google Earth遙感影像，設置了河道結點，將河道分成了虛擬河段，并估算了各個虛擬河道的斷面寬度、側坡及底坡。單元分類及河道虛擬結點和虛擬河段的劃分結果如圖2，其他結果因篇幅限制未列出。

從美國馬里蘭大學全球觀測實驗室與中國科學院地理科學與資源研究所聯合實驗室網站的全球土地覆蓋類型數據庫中(http:∥landcover.usgs.gov)下載了田頭水流域的土地利用類型數據，空間分辨率為1 000 m×1 000 m，通過尺度轉換將其轉換成與DEM一致的空間分辨率。根據田頭水流域的土地利用類型數據，按照流溪河模型中土地利用類型參數的確定方法，確定了邊坡糙率和蒸發系數的初始參數值。

從世界土壤信息(ISRIC)網站的全球土壤類型數據庫中(http:∥www.isric.org/)下載了田頭水流域的土壤類型數據，空間分辨率為1 000 m×1 000 m，通過尺度轉換將其轉換成與DEM一致的空間分辨率。根據田頭水流域的土壤類型數據，按照流溪河模型中土壤類型參數的確定方法，確定了土壤類參數的初始值。

2.3 降雨插值計算

根據泰森多邊形插值計算方法，對本文收集的7場洪水過程中的降雨進行了插值計算，得到了各單元上的相應面雨量。圖3為部分插值計算結果。

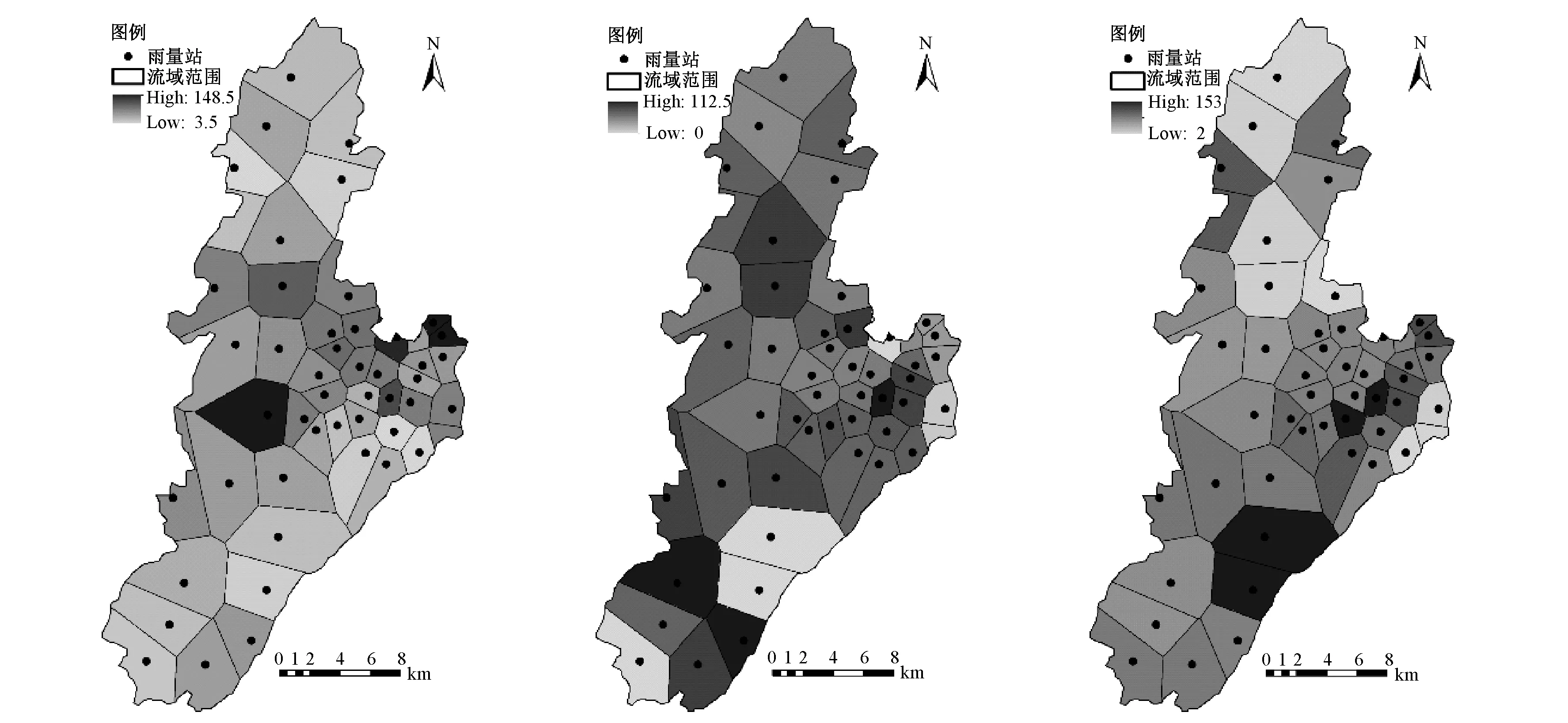
圖3 田頭水流域部分降雨插值計算結果Fig.3 Part interpolation results of Tiantoushui Watershed

2.4 參數自動優選

采用PSO法[18]對田頭水流域流溪河模型12個可調參數進行自動優選。選擇20120412場次洪水進行參數自動優選，圖4為參數優選計算過程中的部分結果。

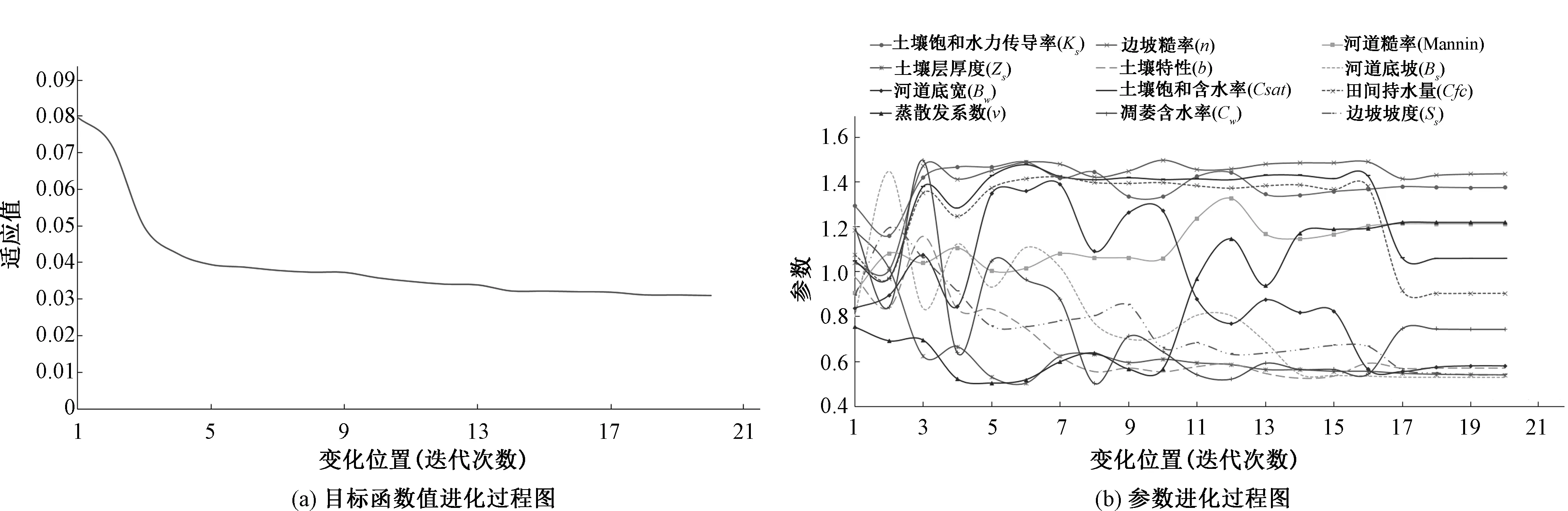
圖4 參數優選過程圖Fig.4 The evolution process of parameter

本文采用權重法，將五個常用目標函數(確定性系數、相關性系數、過程相對誤差、水量平衡系數、洪峰誤差)轉化為單一目標函數進行參數優選。圖4(a)為參數優選過程中目標函數值(適應值)的變化過程，圖4(b)為參數的進化過程。從圖中可以看出，隨著尋優進程的推進，當迭代計算總次數達到18次以后，模型參數值和目標函數值趨近于穩定。

統計該場洪水模擬效果的評價指標，確定性系數為0.919，相關系數為0.973，水量平衡系數為0.854，過程相對誤差為30.9%，洪峰相對誤差為2.7%，峰現時間差為-1 h，洪水模擬的效果優良。

2.5 模型驗證

對2012年到2015年其他的6場洪水進行粒子群算法的適用性驗證，并統計了6個評價指標，包括確定性系數、相關系數，水量平衡系數、相對過程誤差、洪峰誤差，峰現時間差，詳細結果見表1。

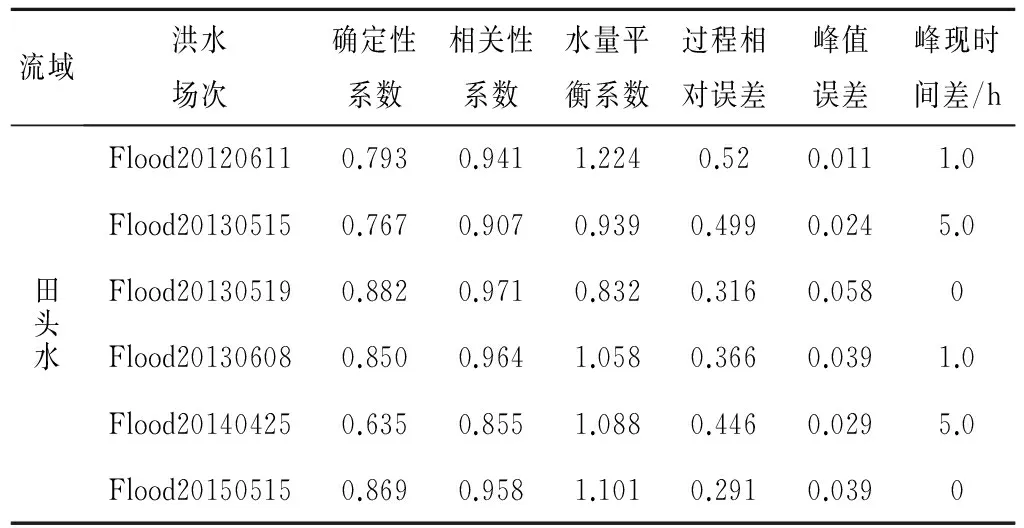
表1 模型驗證結果Tab.1 Simulation results of the model

6場洪水模擬過程線分別如圖5。

統計模擬效果評價指標，6場洪水模擬的平均確定性系數分別為0.80，平均相關系數分別為0.93，平均水量平衡系數分別為1.04，平均過程相對誤差分別為41%，平均洪峰相對誤差分別為3.0%，平均峰現時間差均為2 h，洪水模擬的效果優良。表明采用泰森多邊形法進行流溪河模型單元面雨量插值計算是可行的。

3 結果與討論

3.1 雨量站網密度對插值計算結果的影響

田頭水流域雨量站網密度較高，插值計算結果較理想，但在很多流域，雨量站網密度相對較低。為了探討雨量站網密度對降雨插值計算的影響及對流溪河模型模擬結果的影響，對田頭水流域50個雨量站，分別抽取其中的5、10、20、30、40、50個雨量站，組成6組不同密度的雨量站網。在選取雨量站時，使雨量站在流域內的分布在空間上盡量均勻。各組的雨量站分布和泰森多邊形如圖6。

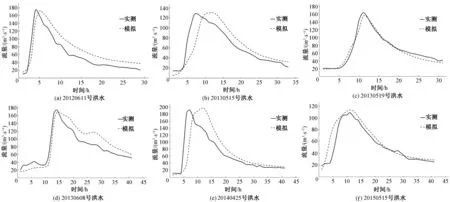
圖5 洪水模擬過程圖Fig.5 Hydrological process of floods

對6場洪水分別進行插值計算，得到不同雨量站網密度不同場次洪水的流域累積面雨量，結果如圖7所示。

從圖7結果可以看出，雨量站個數為10個及以上時，流域累積面雨量趨于穩定，變化不大，但當只有5個雨量站時，流域累積面雨量明顯不同，說明在本文的研究案例中，當雨量站達到10個時，已基本上能充分反映降雨在流域內的空間變化。這一結果說明，雨量站網密度對估算的流域面雨量有明顯影響，當雨量站網密度達到一定值時，雨量站網密度的增加對計算結果的影響不大。

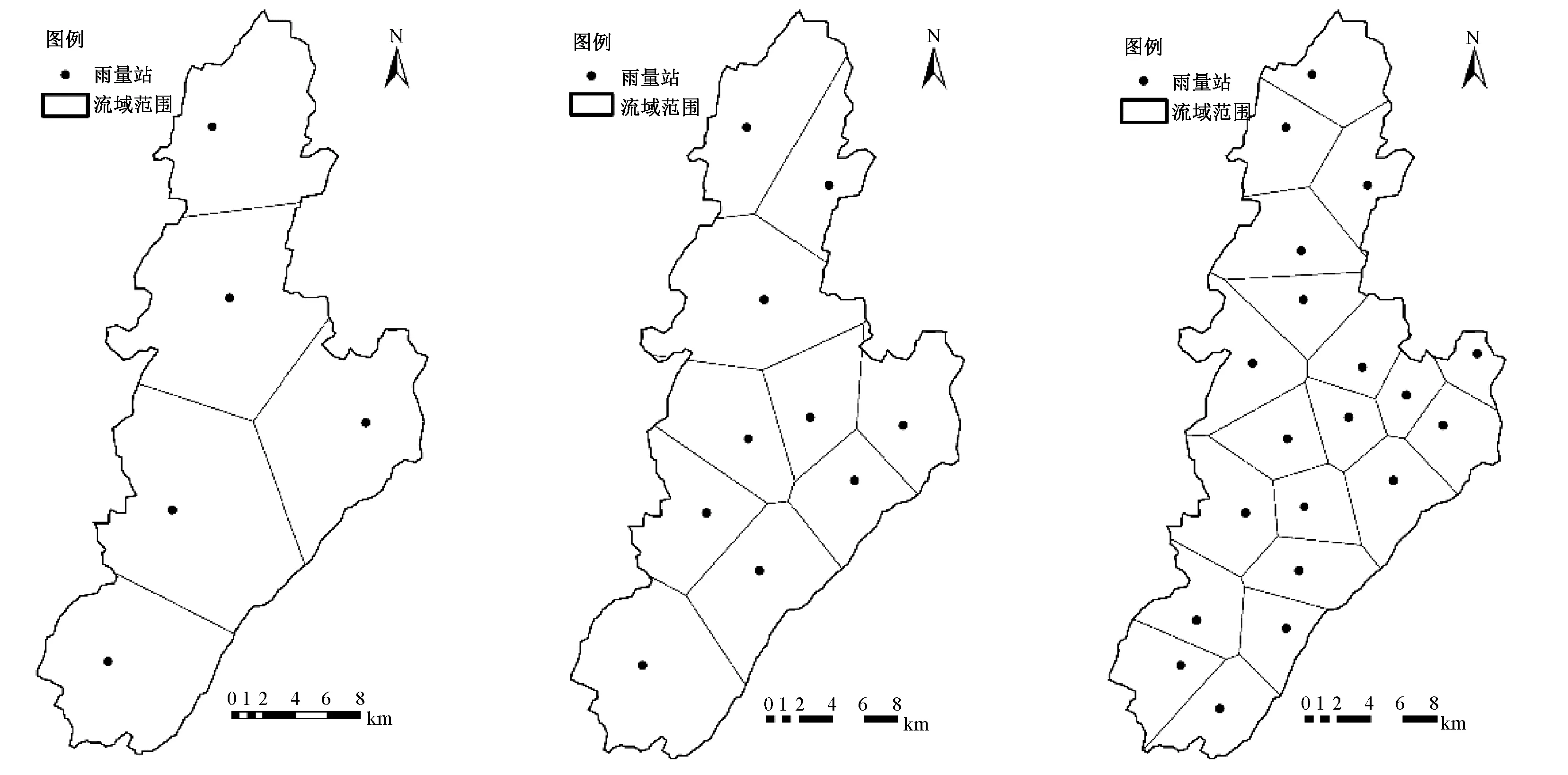
圖6 田頭水流域雨量站點分布和泰森多邊形劃分Fig.6 Distribution of gauges and Thiessen polygon of Tiantoushui Watershed

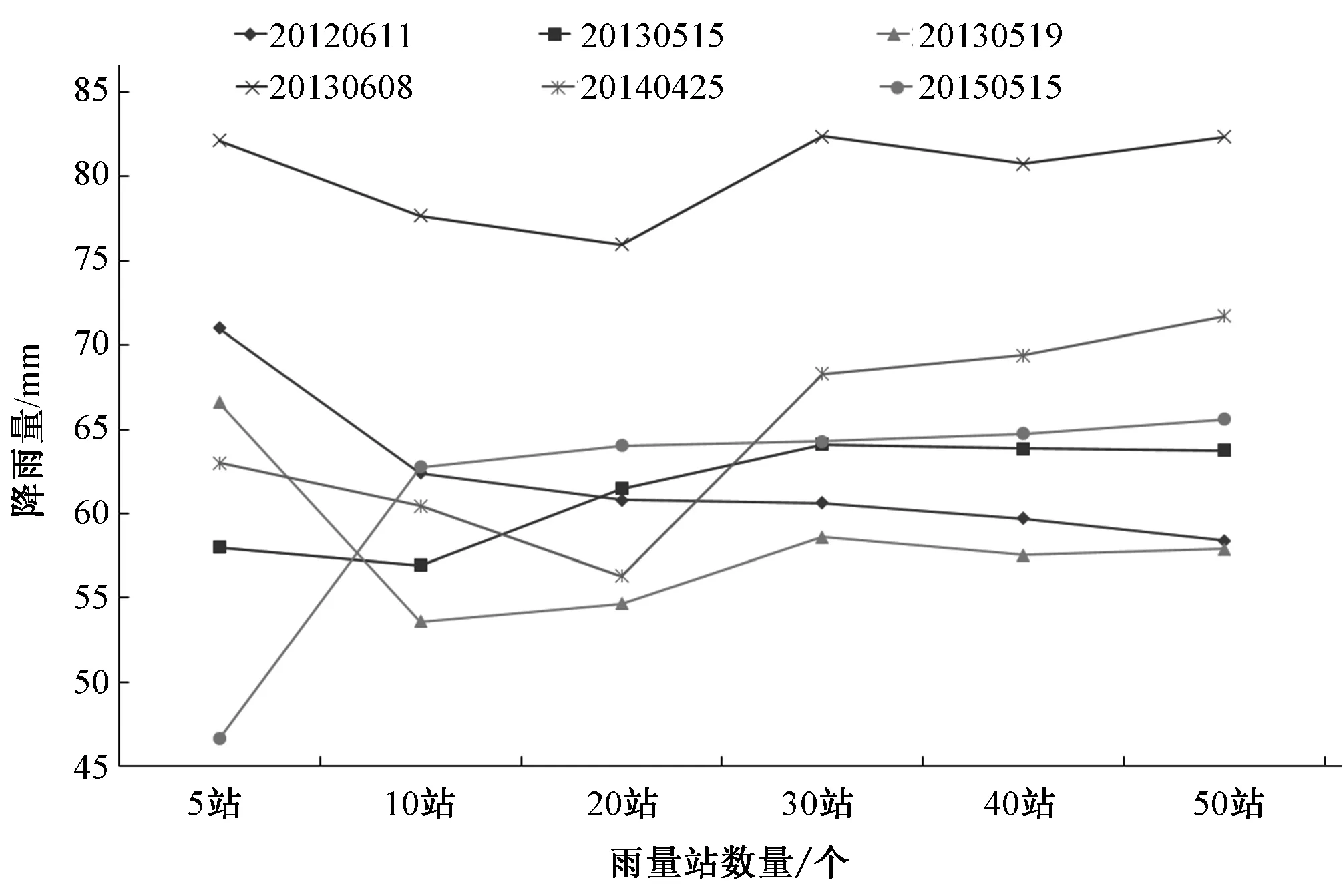
圖7 不同站點密度泰森多邊形法流域面雨量計算結果對比圖Fig.7 The result of rainfall of floods used Thiessen polygon method at different gauge density

3.2 站網密度對流溪河模型參數優選結果的影響

為了分析站網密度對流溪河模型參數優選的影響，利用20120412場次洪水不同站網密度時的降雨插值計算結果，分別進行參數自動優選，結果如圖8。

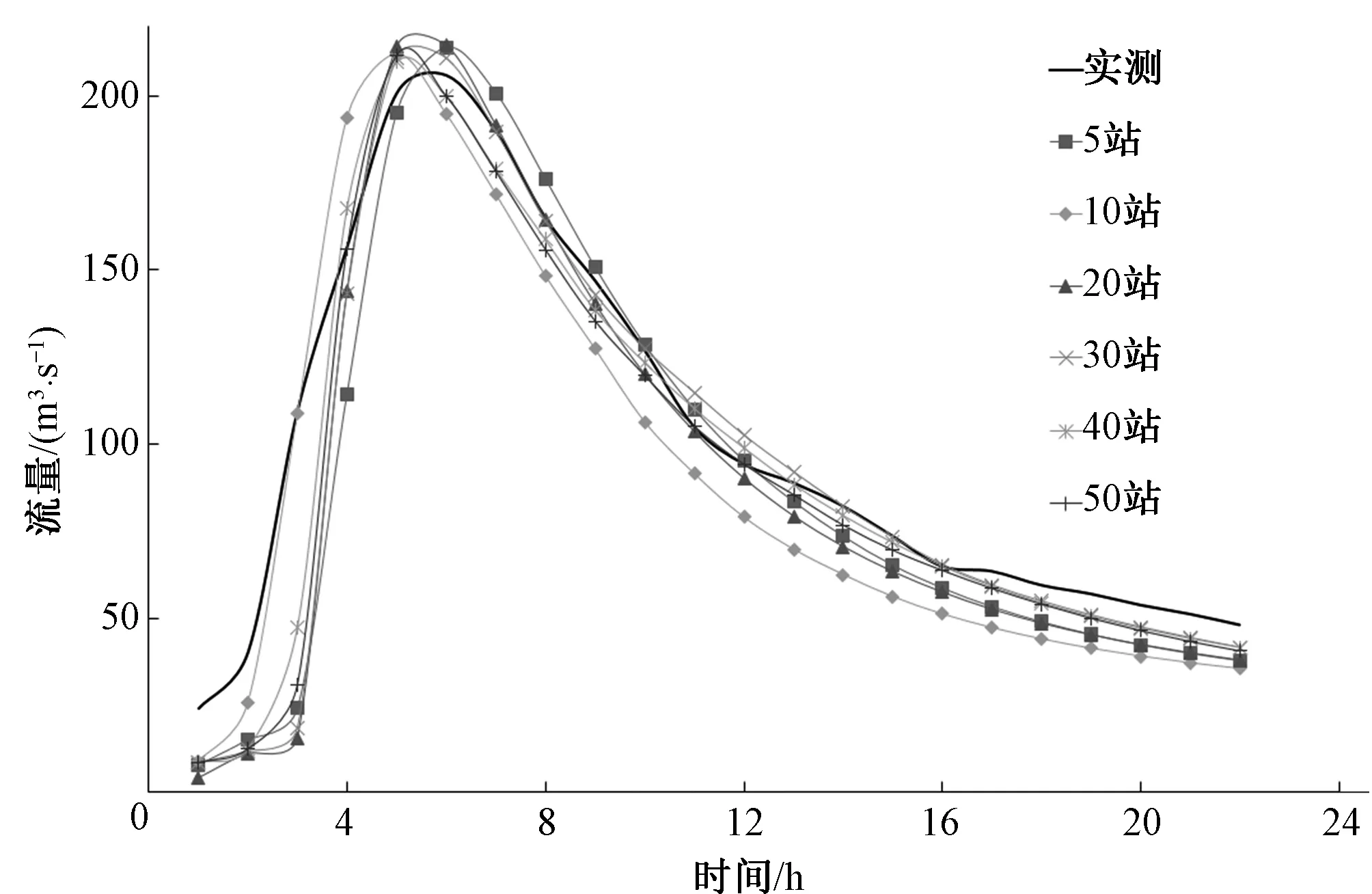
圖8 20120412場次洪水不同站點密度下參數優選結果對比圖Fig.8 Hydrological process comparison simulated with different gauge density

從上述結果看出，站網密度對流溪河模型參數優選結果的影響較小，這說明流溪河模型在進行參數優選時，可在一定程度上消除降雨空間分布的不確定性。

3.3 站網密度對流溪河模型模擬結果的影響

采用20120412場次洪水不同站點密度下優選的模型參數，對六場次洪水不同站網密度的降雨進行了洪水模擬，結果如圖9。

對于前5場次洪水，雨量站點數量從5個變化到50個時，流溪河模型的洪水模擬結果變化較小，可能的原因是本場次洪水的降雨在空間上的變化不大。對于20150515場次洪水，當雨量站個數達到10個后，洪水過程的變化也較小，但當雨量站個數為5個時，模擬的洪水過程與實測值有明顯偏差，這說明5個雨量站不能充分測報降雨的空間分布。這也說明在田頭水流域，當雨量站個數達到10個時，基本上能測報出降雨在空間分布上的不均勻性。

4 結 語

本文提出了基于泰森多邊形法估算流溪河模型單元網格面雨量的方法，針對田頭水流域建立了流溪河模型，采用PSO算法優選了模型參數，模擬了六場實測洪水過程，取得了較好的模擬效果，說明泰森多邊形法適用于流溪河模型洪水預報降雨估算的需要。 分析了站網密度對面雨量估算、流溪河模型參數優選及洪水模擬的影響，發現站網密度增加到一定程度時，估算的流域累積面雨量趨于穩定，要充分測報流域降雨的空間分布不均勻性需要有一定的雨量站網密度，本文稱此為臨界雨量站網密度，在田頭水流域為10個雨量站，即平均50 km2一個雨量站。雨量站網密度對流溪河模型參數自動優選結果的影響不明顯，說明流溪河模型參數優選具有控制降雨空間分布不均勻性所帶來的不確定性的效果。雨量站網密度達到臨界值后，利用流溪河模型模擬洪水時的變化不大。

□

[1] 陳洋波,任啟偉,徐會軍,等.流溪河模型I:原理與方法[J].中山大學學報(自然科學版),2010,49(1):105-112.

[2] 陳洋波, 黃鋒華, 徐會軍,等. 流溪河模型Ⅱ:參數推求[J].中山大學學報(自然科學版), 2010,47(2), 95-102.

[3] A H Thiess.Climatological data for July,1911[J].Monthly Weather Review,1991.

[4] Drozdov D A, A A Sephelevskii. The theory of interpolation in a stochastic field of meteorological elements and its application to meteorological maps and network regionalization problems (in russian)[J]. Trudy NIU GUGMS l(18).

[5] Shepard D. A two-dimensional interpolation function for irregularly spaced data[C]∥ Proceedings of the 1968 ACM National Conference,1968:517-524.

[6] John C Davis. Statistics and data analysis in geology[M]. John Wiley and Sons, New York,1986.

[7] Christopher Daly. The prism approach to mapping precipitation and temperature[C]∥In proceedings 10th AMS Conference on Applied Climatology.American Meteorological Society:Reno,NV,20-23 October,1997:10-12.

[8] M F Hutchinson. Interpolation of rainfall data with thin plate smoothing splines - Part I: two dimensional smoothing of data with short range correlation[J]. Journal of Geographic Information and Decision Analysis,1998,2(2):139-151.

[9] 王名才.大氣科學常用公式[M].北京:氣象出版社,1994:518-519.

[10] Guillermo Q TabiosIII, Jose D Salas. A comparative analysis of techniques for spatial interpolation of precipitation[J]. Water Resources Bulletin,1985,21(3):365-380.

[11] 徐 晶,林 建,姚學祥,等.七大江河流域面雨量計算方法及應用[J]. 氣象,2001,27(11):13-51.

[12] 畢寶貴,徐 晶,林 建. 面雨量計算方法及其在海河流域的應用[J]. 氣象,2003,29(8):39-42.

[13] 朱求安,張萬昌.流域水文模型中面雨量的空間插值[J]. 水土保持研究,2005,12(2).

[14] 王國慶,張建云,張 明,等. 雨量站網密度對不同氣候區月徑流模擬的影響[J]. 人民長江,2009,40(8):45-49.

[15] 陽 帆,王漢濤,黎曉東.雨量插值方法對BTOPMC模型及洪水模擬的影響[J]. 人民黃河,2012,34(5):16-19.

[16] 沈 冰,黃紅虎.水文學原理[M].2版.北京:中國水利水電出版社,2005.

[17] 胡建華.赤溪水文站場次洪水降雨徑流情況分析[J].廣東水利水電,2008,(6):28-30.

[18] Yangbo Chen, Ji Li, and Huijun Xu. Improving flood forecasting capability of physically based distributed hydrological models by parameter optimization [J]. Hydrol. Earth Syst. Sci., 2016,20:1-18.