美國混凝土學會（ACI）混凝土強度標準的主要問題

戴鎮潮

美國混凝土學會（ACI）混凝土強度標準的主要問題

戴鎮潮

本文評析美國混凝土學會（ACI）強度標準存在的主要問題：（1）只將預期強度按正態分布計，沒有將設計強度也按正態分布計，而是按定值（或單值）計；（2）沒有全面準確地按數理統計方法確定配制強度和驗收強度。建議應作重大改進。

定值；單值；正態分布；平均值；標準差；抽樣檢驗；試件組

1 ACI 混凝土強度標準簡介

美國混凝土學會（ACI）現行的混凝土強度標準規定于ACI 214R—2011《混凝土強度試驗結果評估指南》和 ACI 318—2011《結構混凝土建筑規范要求》中。

ACI 214R—2011 沒有規定驗收強度 fa的確定方法，只規定了配制強度 fcr的確定方法。當沒有足夠歷史數據預估強度標準差 S 時，按表 5.2 確定 fcr；當有足夠歷史數據預估強度標準差 S 時，按表 5.3 計算 fcr。現分別轉錄于表 1 和表 2。

ACI 318—2011 規定 fcr的確定方法為：當沒有足夠歷史數據預估 S 時，確定 fcr和 ACI 214R—2011 相同，如表 1；當有足夠歷史數據預估 S 時，按表 5.3.1.2 計算 fcr，轉錄于表3。

ACI 318—2011 也規定了驗收強度。其第 2.6.3.3 條規定：當符合以下兩項要求時即認為某一等級混凝土的強度水平達到了要求：

a. 任何連續 3 組試件強度平均值等于或大于 fc′。

b. fc′ ≤5000psi 的混凝土，任何 1 組試件強度都不低于fc′-500psi；fc′＞5000psi 的混凝土，任何 1 組試件強度都不低于

且只允許低于這些規定的 100 次中大約有 1 次。

于是得 ACI 318—2011 規定的連續 3 組試件強度平均值的驗收強度 fa和試件強度最小值的驗收強度 fmin列于表 4。

表4 ACI 318—2011 規定的混凝土驗收強度

2 ACI混凝土強度標準解析

表1 ACI 214R—2011 表 5.2 規定的配制強度 fcr的計算公式

表2 ACI 214R—2011 表 5.3 規定的配制強度 fcr的計算公式

表3 ACI 318—2011表 5.3.1.2 規定的配制強度 fcr的計算公式

2.1 預估強度標準差

表1 是當沒有足夠歷史數據預估 S 和 V 時，fcr的計算式。fcr大約比 fc′ 高 0.2～0.4fc′。

表2 是當有足夠歷史數據預估 S 和 V 時，fcr的計算式。S 和 V 由前 24 個月內獲得的同一批或近似同一批（強度變化不超過 1000psi）混凝土不少于 30 組試件的強度計算得。當試件組數 n 達不到 30 組，為 15～30 組時，強度標準差 S 需乘以表 5 大于 1 的修正系數后再用來計算 fcr；當 n 少于 15組，則按表 1 確定 fcr。

表5 ACI 214R—2011和 ACI 318—2011規定的試件組數達不到 30 組強度標準差 S 的修正系數

ACI 214R—2011 和 ACI 318—2011 認識到 n 少時 S 具有很大的不定性，且大多偏小，計算得的 fcr偏低，是不安全的，故列出表 5 的修正系數。但據筆者計算，n 達到 30 組，S 仍具有很大的不定性，且大多仍偏小，還要乘以大于 1 的修正系數。n 要達到 200 組以上，S 才較穩定，且和總體強度標準差 σ 相近，修正系數見表 6。

由于獲得 200 組以上的試件強度一般較困難，建議依據歷史數據，同時評估實際質量控制水平及混凝土強度，直接預估得總體強度標準差 σ，還可能準確、方便些。

2.2 應用強度標準差 S 還是變異系數 V

ACI 214R—2011 同時應用 V 和 S 的計算公式（見表2），ACI 318—2011 只應用 S，不再應用 V 來計算 fcr（見表3）。后者是正確的。因為 V 由 S 和平均值 fcr衍生而得，即V=S/fcr。將其代入表 2 的式 (5-1a)、(5-2a)、(5-3a)、(5-4a)，就可得表 2 的式 (5-1b)、(5-2b)、(5-3b)、(5-4b)。所以兩者計算得的結果應該完全相同，而應用 S 則直接、方便。ACI 214R—2011 第 5.3.1 條、第 5.3.2 條、第 5.3.3 條應用 S 和應用 V 計算的配制強度不同，其原因是分別預估得的 S 和 V，V≠S/fcr。

最早的版本 ACI 214—57、ACI 214—65 只應用 V 計算fcr，是認為 V 是相對指標，不會隨強度高低而變化。后來大量實測結果表明，V 和 S 都隨強度高低而變化，于是 ACI 214—77 改為同時應用 V 和 S 計算的 fcr，直至現在的版本ACI 214R—2011。

2.3 風險率 p、強度保證率 P 和保證率系數 Z

表2 中 S 或 V 前面的系數 Z 為與允許預期強度分布低于指定強度（如表 2 中的 fc′、fc′-k、kfc′）的概率（風險率）p 相應的正態偏差的絕對值。中國習慣采用強度保證率 P（P=1-p），稱 Z 為保證率系數。最早的版本 ACI 214—57、ACI 214—65 只規定低于指定強度 fc′ 的 p 的規定摘錄于表 7。

ACI 214—77 不再規定允許強度低于 fc′ 的概率。只引用ASTM C94—74 的建議：對于按極限強度設計的混凝土低于fc′ 的試件組數不得超過總數的 10%，其它混凝土沒有說明。

ACI 214—77 又引用 ACI 318—71 的建議：由一工程取得足夠數據后，連續 3 組試件強度平均值低于 fc′ 的概率，不應超過 1%；又在表 4.3 第 3 列以試件強度低于 fc′-500psi 的概率不超過 1% 來確定 fcr；在舉例中還以試件強度低于 0.85fc′ 的概率不超過 1% 來確定 fcr。這就開始以 p=1%（P=99%），相應的 Z=2.33 來計算 fcr，但基準強度不再是 fc′，而是比 fc′ 小的其它強度值，ACI 318—2011 就采用 fc′-500psi 和 0.9fc′。

2.4 計算配制強度的基準強度和驗收強度

fcr計算式表明，fcr由基準強度+保證強度而成。前面已說明，早先基準強度采用 fc′，加上保證強度后所得的 fcr肯定大于 fc′。fcr應大于（不能等于，更不能小于）fc′。這樣才能使實際強度有較大的把握達到 fc′。基準強度采用比 fc′ 小的其它強度值，計算得的 fcr是否大于 fc′ 是不明確的。當采用的基準強度很低、S 很小時，計算得的 fcr可能會小于 fc′。

表3 和表 4 表明，ACI 318—2011 計算 fcr采用的基準強度fc′、fc′-500psi 和 0.9fc′。其中 fc′ 是連續 3 組試件強度平均值的驗收強度 fa，fc′-500psi 和 0.9fc′ 則是試件強度最小值的驗收強度 fmin。這些驗收強度都是憑經驗指定的，缺乏科學依據（詳見后述）。比如為什么是連續 3 組試件強度平均值的驗收強度 fa= fc′，不是連續 4 組或 5 組……；又為什么是 fc′-500psi，不是 fc′-400psi 或 fc′-300psi……；又為什么是 0.9fc′，不是 0.85fc′ 或 0.80fc′。所以用它們作為計算 fcr的基準強度并不妥當。

3 ACI 混凝土強度標準的主要問題

表6 筆者計算得的不同試件組數 n 試件強度標準差 S 的修正系數 d (dS＜σ的概率≯20%)

表7 ACI 214—57、ACI 214—65 允許強度低于設計強度 fc′ 的概率（失效概率）的規定

ACI 混凝土強度標準的主要問題是：（1）設計強度沒有按正態分布計；（2）沒有全面準確運用數理統計方法。茲分別加以評析。

3.1 設計強度沒有按正態分布計

混凝土強度按正態分布計，已被普遍認同。但是 ACI 混凝土強度標準只將預期強度按正態分布計，而將設計強度按定值（或單值）計（見圖 1-(2)）。這是該標準最根本的錯誤。導致不能完全消除經驗因素和不能全面準確運用數理統計方法，致使最終確定的配制強度和驗收強度不正確。

混凝土強度都按正態分布計，且設標準差 σ 不隨強度變化，則 fcr為預期強度平均值，預期強度正態分布為 N(fcr, σ2)，fc′ 則為設計強度平均值，按正態分布計的設計強度就是N(fc′, σ2)，以虛線示于圖 1-(2)。于是在此基礎上全面運用數理統計方法的一次計量抽樣檢驗方案，考慮試件組數 n 和抽樣檢驗的兩類錯誤 α、β，確定合理的配制強度及驗收強度，方法略。

3.2 沒有全面準確運用數理統計方法

3.2.1 仍憑經驗確定配制強度

早先，在沒有認識到混凝土強度是隨機變量，并按正態分布計以前，都將混凝土強度當作定值，即以為混凝土完全均勻，一種混凝土只有一個強度，fcr按式 (1) 計算得，示于圖1-(1)。

式中：

k——強度加成系數，憑經驗確定，通常取 1.1～1.2。

ACI 現在仍在采用此方法，見表 1。

在認識到混凝土強度是隨機變量，并開始按正態分布計時，只將預期強度按正態分布計，為 N(fcr, σ2），fcr改按式(2) 計算，示于圖 1-(2)。

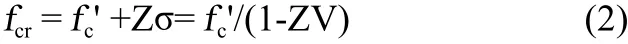
式中：

σ——強度標準差；

V——強度變異系數，V=σ/fcr；

Z——系數，取決于強度允許低于設計強度 fc′ 的概率（風險率）p，列于表 8。

表8 Z 值

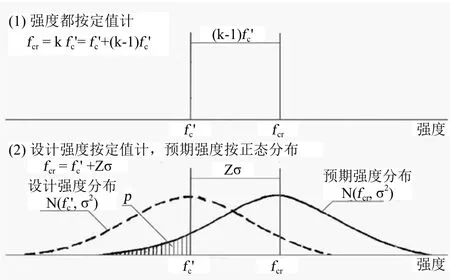
圖1 配制強度確定方法圖示

這是 ACI 在 20 世紀 50 年代開始采用現在仍在采用的方法，見表 2 和表 3。由于只將預期強度按正態分布計，為N(fcr, σ2)，沒有將設計強度也按正態分布計，而是仍和經驗法一樣當作定值（或單值），為 fc′；還由于低于設計強度 fc′的概率 p 憑經驗確定，與 p 相應的 Z 值也是經驗值，則式(2) 計算得的 fcr也仍是經驗值，雖然考慮了強度變異性（σ 或V），采用了概率計算（并不全面），但與式 (1) 沒有實質區別。

3.2.2 試件強度平均值的驗收強度按假設檢驗法確定，采用的數理統計方法不準確

該規定很可能來源于 ACI 214 以前的幾個版本，現摘錄于表 9。

表9 中，試件組數 n=3 的驗收強度等于或十分接近于fc′。這很可能就是 ACI 318—2011 規定的連續 3 組的驗收強度 fa= fc′ 的依據。

但是必須指出的是，表 9 中 ACI 214 以前的幾個版本 的fa都隨 n 的增多而增大。這是“獎懶罰勤”，誰愿意去多取試件呢？是不合常情的。抽取的 n 增多，的精密度提高（即平均值的標準差減小），估計實際強度平均值（真值）的誤差減小，驗收強度 fa應隨 n 的增多而降低（同理，fcr也降低），所以 ACI 214 以前的幾個版本的驗收強度fa隨 n 增多而增大是不符合統計規律的。這是因為采用的數理統計方法不準確，即采用假設檢驗法的結果。下面以 ACI 214—77 規定的預估得 σ 的驗收強度為例，繪成圖 2 加以說明。

圖2 中，先以低于 fc′ 的概率（風險率）p=10% 用虛線繪得預期強度分布 N(fcr, σ2) 及 fcr，fcr= fc′+1.28σ；再繪得從 N(fcr,

表9 ACI 214 以前的幾個版本試件強度平均值的驗收強度摘錄

σ2) 中抽取的的分布 N(fcr, σ2/n) ；再按該規定的說明：“在指定的試驗次數時，其平均值低于表列驗收強度的可能性僅為 2%。”知其的 fa按假設檢驗法單側顯著性水平（即抽樣檢驗的第Ⅰ類錯誤）α=2% 確定，即繪得其中 -2.05 是 α=2% 的正態偏差 tα。也就是試件強度平均值的驗收強度 fa是 n 組試件強度平均值的分布 N(fcr, σ2/n) 的 2% 分位值。于是得 fa的計算式為：

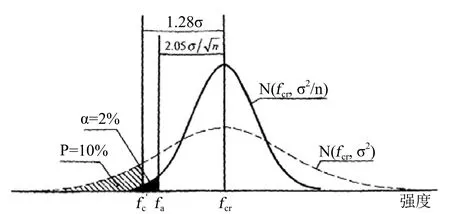
圖2 ACI 214—77 混凝土試件強度平均值的驗收強度 fa的確定方法圖示

圖2 表明，由于 fcr不隨試件組數 n 變化，而預期的分布 N(fcr, σ2/n) 隨 n 增大，因標準差減小，由寬而平變得窄而尖，向中間（平均值 fcr）靠攏，其 2% 分位值即 fa也向 fcr靠攏而不斷增大，最終趨近于 fcr（n→∞時）。

3.2.3 試件強度最小值的驗收強度憑經驗指定

ACI 318—2011規定 fc′≤5000psi 的混凝土，任何一組試件強度都不得低于 fc′-500psi；fc′＞5000psi 的混凝土，任何一組試件強度都不得低于 0.9fc′。即規定 fc′≤5000psi 的混凝土，fmin= fc′-500psi；fc′＞5000psi 的混凝土，fmin=0.9fc′。

fmin主要是用來檢驗強度標準差 σ 的。σ 增大，fmin應提高，相反則應降低。統計規律表明，觀測值（如試件強度）的最小值 xmin是隨機變量，隨觀測次數（如試件組數）n 的增大而減小（相應地最大值 xmax則隨 n 的增大而增大，亦即極差增大），所以 fmin也應隨試件組數 n 的增多而降低。由于試件強度應同時達到：才能判為合格；而且

ACI 318—2011 規定的 fmin，與 σ、n 無關；也不與 fa相關連，很可能是憑經驗指定的。

3.2.4 驗收強度用作確定配制強度的基準強度，合格的概率只有 50%

4 結論

（1）美國混凝土學會（ACI）混凝土強度標準的最主要問題只將預期強度按正態分布計，沒有將設計強度也按正態分布計，而是按定值（或單值）計，因而不能全面準確地運用數理統計方法確定配制強度和驗收強度。

（2）美國混凝土學會（ACI）混凝土強度標準確定的fcr，雖然也部分應用了數理統計方法，但最終所得的依然都是經驗值。規定連續 3 組的 fa=fc′，來源于不準確的統計方法——假設檢驗法，而且只規定連續 3 組的驗收強度也不合理。xmin的驗收強度 fmin都憑經驗指定，與 σ、n 無關，也不與 fa相關連。將驗收強度 fa、fmin作為確定 fcr的基準強度，結果實際強度將只有 50% 的達到設計要求。

（3）建議美國混凝土學會（ACI）混凝土強度標準應作重大改進。最根本的是將設計強度也按正態分布計和運用符合混凝土強度的數理統計方法。

［通訊地址］重慶市渝中區民生路 318 號 4-8-2（400010）

戴鎮潮（1934—），男，武警水電第二總隊退休高級工程師。