基于雙交叉和特征的快速分形圖像編碼研究

張 璟，張愛華，汪瑋瑋，唐婷婷

(南京郵電大學 理學院，江蘇 南京 210023)

基于雙交叉和特征的快速分形圖像編碼研究

張 璟，張愛華，汪瑋瑋，唐婷婷

(南京郵電大學 理學院，江蘇 南京 210023)

針對傳統基本分形編碼存在的計算復雜性較高、編碼時間較長的缺點，提出了一種基于雙交叉和的特征值編碼算法，以解決分形圖像編碼時間過長的問題。該算法通過構造圖像塊適當的特征向量，將“R在D集合中搜索MSE意義下的最佳匹配塊”問題轉換成“R的特征向量在D的特征向量空間中搜索最佳匹配塊”的問題，將全局搜索轉化為相對意義下的近鄰搜索，使得匹配搜索只在初始匹配塊的鄰域內進行，有效地減少了搜索對象，從而進一步加快了編碼速度。采用圖像方塊分割進行了多種算法的對比仿真實驗，實驗結果表明相對于其他算法，所提出的算法在保證一定重建圖像質量的前提下，提高了圖像的結構相似度，圖像編碼時間明顯縮短，較好地實現了提高算法編碼速度的目的。

分形；分形圖像編碼；特征向量法；雙交叉和特征

0 引 言

當今信息時代，人們在面對大量圖像信息數據時，如何進行高效率的存儲和傳輸，成為了一個重要問題。而對于提高存儲和傳輸的效率，不僅僅只依賴硬件設備自身的更新換代，也需要高性能圖像壓縮技術的研究予以支持。分形幾何[1]作為新興數學的一個分支，對描述自然界中那些不規則的幾何形狀提供了幫助，在圖像編碼鄰域也得到了廣泛的應用。

基于分形的圖像壓縮編碼[2]方法是一種新的編碼方法，它是利用圖像的自相似性以及比例特性，通過消除圖像的幾何冗余度來實現圖像數據的壓縮。在分形編碼中，一幅圖像由一組使它近似不變的壓縮仿射變換來表示，重構圖像是壓縮變換的不動點，壓縮仿射變換的參數組成原始圖像的分形碼。相對來說，這是一種簡單的快速迭代過程，解碼圖像由解碼表示的壓縮變換迭代作用于任意初始圖像來逼近[3]。

分形圖像壓縮編碼的主要特點是：在獲得高壓縮比的同時還能夠保持較好的解碼圖像質量，運算速度與提高圖像分辨率的關系不大，選擇合適的分形模型可以構造出較清晰的邊緣細節，解碼過程快捷，等等。但與此同時，其計算復雜性較高、編碼時間較長的缺點也尤為顯著，已經嚴重影響到了分形編碼的廣泛應用[4]。因此在保證圖像質量不變或更好的前提下，如何加快編碼也是分形編碼的一個重要課題。而基于特征向量法的快速分形編碼算法就實現了這一目標，通過構造圖像塊適當的特征向量，將全局搜索轉化為相對意義下的近鄰搜索，減少了搜索對象，從而加快了編碼速度。

文中所依據的特征向量法是Saupe提出的一種快速分形編碼方法[5]，約定碼本Ω中的碼本塊都按某種方式向量化，即D∈Ω表示線性空間Rn中的向量(n=N×N,N×N是碼本塊D的尺寸)。它首先構造圖像塊X塊(R塊和D塊)的特征向量φ(X)，然后證明極小化MSE(R,D)的問題等價于極小化Δ(R,D)的問題：

Δ(R,D)?min(d(φ(R),φ(D)),d(-φ(R), φ(D)))

(1)

其中，d是歐氏距離。

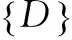
d(FR,FD)≤δ?MSE(R,D)≤ε

(2)

其中，FX為圖像塊X的特征向量；δ>0、ε>0為適當閾值。

所以，如何選取特征向量以及在特征向量空間中的搜索方法是特征向量法的關鍵。

文中選取規范化圖像子塊水平、垂直中位線，以及兩條對角線所在直線構成的雙交叉上像素點的灰度值作為特征點，以這些特征點的歸一化值的絕對值之和來定義圖像規范塊雙交叉和的特征；先在理論上證明了雙交叉和與均方誤差的關系不等式，再對碼本Ω中的碼本塊按照每一塊雙交叉和的大小進行排序，在編碼每一R塊時，使用二分法在賦序碼本中找出其初始匹配塊，之后的匹配搜索便直接在初始匹配塊的鄰域內進行[7-8]。

1 算 法

1.1 算法理論依據

首先給出雙交叉和特征的定義：

定義1：設子塊X=(xi,j)∈RN×N，X的規范化為：

(3)

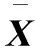
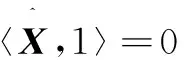
S(x)=

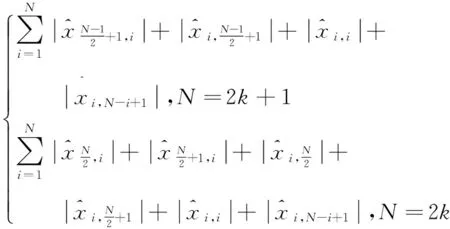
(4)

即雙交叉和為規范塊垂直水平交叉線和對角線(構成形如“×”“+”形狀的兩個交叉的結構)上每個像素點灰度值的絕對值之和。

理論基礎為下述定理，參考并給出證明：

定理1：設R,D∈RN×N,則有下面的不等式成立：

(5)

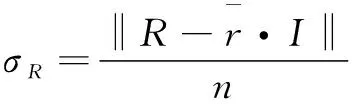
(6)

有：

(7)

由柯西不等式：

(8)

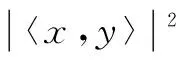
(9)

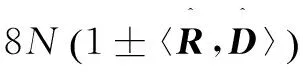
(10)

而約束條件為：

(11)

證畢。

1.2 算法分析與實現

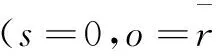
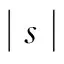
顯然，N(Dinit,k)?Ωη?Ω。搜索空間由全局搜索變為局部搜索，編碼時間會隨著搜索空間的縮小而減少，從而加快編碼速度。對于不同的k值，編碼加速的程度有所不同[13-14]。

2 仿真實驗及結果分析

文中圖像采用方塊分割，仿真使用的圖像是256×256，8bit量化的Lena圖像。選取R塊大小為8×8，D塊大小為16×16，步長σ=16。操作平臺為運行Windows7的IntelPentium(2.00GHzCPU/2.00G內存)PC，仿真程序使用MATLABr2012b編寫，測試參數為編碼時間(s)、峰值信噪比(PSNR)(dB)和結構相似度(FSIM)[15]。

通過實驗將文中算法與基本算法以及1-范數算法[16]的編碼性能進行比較：雙交叉和特征算法的編碼時間與解碼圖像質量跟R塊的分類閾值τ，容許碼本閾值參數η，搜索鄰域半徑大小k有關。根據文獻[9]，對于參數τ和η，固定其取值，默認τ=4，η=3。根據Lena圖像的實驗數據，三種算法比較結果見表1。

搜索鄰域半徑K取不同值時，三種算法的實驗效果如圖1～3所示。

表1 基本分形算法、1-范數算法與文中算法對比結果

從表中數據分析可得，雙交叉和特征算法與基本分形算法及1-范數算法相比，從主觀上看，基于雙交叉和特征算法基本上不改變重構圖像的質量；從客觀上看，相比于1-范數算法，文中算法在略微提高性噪比的基礎上，大幅減少了運算時間，且提高了結構相似度，與基本分形算法相比，該算法并沒有降低太多信噪比，且編碼速度比之快了6倍，結構相似度也顯著提高。綜上所述，文中算法可以在保證一定圖像質量的前提下，大幅提高編碼速度和結構相似度。

圖1 k=1的實驗結果圖

圖2 k=2的實驗結果圖

圖3 k=3的實驗結果圖

3 結束語

由于傳統基本分形編碼有著計算復雜性較高、編碼時間較長的缺點，依據特征向量法提出了一種基于雙交叉和特征向量的改進方法。通過尋找最佳匹配塊的方式，在不影響圖像質量的前提下，縮短了圖像編碼時間，實現了編碼速度的提升，并提高了圖像的結構相似度。而且文中算法引進了參數搜索鄰域半徑k，可以針對不同場合的需要來選擇合適的k值，有較強的靈活性和實用性。

實驗結果表明，該算法相對于基本分形算法，編碼效率更高，應用前景更加廣闊。

[1] 法爾科內.分形幾何-數學基礎及其應用[M].第2版.北京:人民郵電出版社,2007.

[2]GalabovM.Fractalimagecompression[C]//Proceedingsofthe4thinternationalconferenceoncomputersystemsandtechnologies:e-learning.[s.l.]:ACM,2003:347-361.

[3] 齊利敏,劉文耀,呂大偉.基于分形的快速壓縮編碼方法[J].西安電子科技大學學報:自然科學版,2008,35(2):373-376.

[4] 馮 曄,馮忠義,朱幼蓮,等.分形編碼技術的介紹與展望[J].常州技術師范學院學報,1999,5(2):1-6.

[5] 何傳江,蔣海軍,黃席樾.快速分形圖像編碼的一種特征方法[J].電子學報,2004,32(11):1864-1867.

[6]WohlbergB,JagerGD.Areviewofthefractalimagecodingliterature[J].IEEETransactionsonImageProcessingAPublicationoftheIEEESignalProcessingSociety,1999,8(12):1716-1729.

[7] 何傳江,申小娜.改進分形圖像編碼的叉跡算法[J].計算機學報,2007,30(12):2156-2163.

[8]LaiCM,LamKM,SinWC.Improvedsearchingschemeforfractalimagecoding[J].ElectronicsLetters,2002,38(25):1653-1654.

[9] 何傳江,黃席樾.基于圖像塊叉跡的快速分形圖像編碼算法[J].計算機學報,2005,28(10):1753-1758.

[10]LeeCK,LeeWK.Fastfractalimageblockcodingbasedonlocalvariances[J].IEEETransactionsonImageProcessingAPublicationoftheIEEESignalProcessingSociety,1998,7(6):888-891.

[11]HartensteinH,SaupeD.LosslessaccelerationoffractalimageencodingviathefastFouriertransform[J].SignalProcessingImageCommunication,2010,16(4):383-394.

[12] 袁宗文,魯業頻,楊漢生.半叉跡特征的快速分形圖像編碼[J].計算機工程與應用,2016,52(3):197-201.

[13] 李高平,楊 軍,陳毅紅.改進轉動慣量特征的快速分形圖像編碼算法[J].計算機工程與應用,2013,49(24):144-148.

[14] 張思思,劉 宇,趙志濱,等.一種基于相鄰匹配的分形圖像檢索算法[J].計算機科學,2015,42(12):292-296.

[15]ZhangLin,ZhangLei,MouXuanqin.FSIM:afeaturesimilarityindexofimagequalityassessment[J].IEEETransactionsonImageProcessing,2011,20(8):2378-2386.

[16]HeC,YangSX,XuX.Fastfractalimagecompressionbasedonone-normofnormalizedblock[J].ElectronicsLetters,2004,40(17):1052-1053.

Investigation on Fast Fractal Image Encoding with Sum of Double Cross Eigenvalues

ZHANG Jing,ZHANG Ai-hua,WANG Wei-wei,TANG Ting-ting

(School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

For the shortcomings of high computational complexity and long encoding time of the traditional fractal coding,an encoding algorithm based on the sum of double cross eigenvalues is proposed in order to solve the problem of long encoding time.The problem,RsearchforthebestmatchingblockofMSEsenseintheDset,isconvertedintoanotherone,theeigenvectorofRsearchforthebestmatchingblockofDintheeigenvectorspace.Thus,globalsearchistransformedintoneighborsearchbyconstructingsuitablefeaturevectorfortheimageblockintheoppositesenseandmatchingsearchiscarriedoutonlyinthefieldoftheinitialmatchingblock,whichreducessearchobjectsandthenspeedsupencoding.Throughcomparativesimulationexperiment,avarietyofalgorithmsarecomparedandsimulatedbyusingimagesegmentation.Theresultsofexperimentsshowthatthealgorithmpresentedhasimprovedthefeaturesimilarityandreducestheimageencodingtimemoreeffectivelyunderthepremiseofensuringqualityofthereconstructedimage,andthatthepurposeofimprovingtheencodingspeedprocedurehasbeenachieved.

fractal;fractal image coding;eigenvector method;sum of double cross eigenvalues

2016-04-21

2016-08-10

時間：2017-02-17

國家自然科學基金面上項目(11471114,61372125)

張 璟(1991-)，男，碩士研究生，研究方向為非線性分析及應用；張愛華，教授，碩士生導師，研究方向為非線性分析。

http://www.cnki.net/kcms/detail/61.1450.TP.20170217.1628.032.html

TP

A

1673-629X(2017)03-0159-04

10.3969/j.issn.1673-629X.2017.03.033