從判斷二面角的鈍銳說開去
福建省龍海第一中學新校區(363100) 蘇藝偉
從判斷二面角的鈍銳說開去
福建省龍海第一中學新校區(363100) 蘇藝偉
在湘教版選修2-1的學習中,學生接觸到了利用坐標法求解二面角的余弦值.教材介紹的方法是分別求出兩個半平面的法向量,再利用向量夾角公式算出這兩個法向量夾角的余弦值,最后結合圖形得到所求二面角的余弦值.在最后一步往往需要結合圖形對該二面角是鈍角還是銳角作出判斷.對于較為簡單直觀的圖形還容易判斷,如果是較為復雜不明顯的圖形,學生很難區分出來.那么該如何用數學符號語言給出嚴謹的判斷?除此之外是否可以避開這個難點而直接計算出二面角的余弦值?筆者在長期的教學實踐中總結了如下規律.
一、如何判斷鈍角還是銳角?
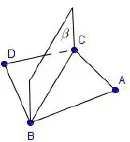
圖1

圖2
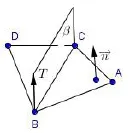
圖3

圖4
如圖(1)所示,觀察圖形可知二面角A-BC-D為鈍角;如圖(2)所示,觀察圖形可知二面角A-BC-D為銳角.那么如何用數學符號語言來進行嚴謹的判斷?
作出經過公共棱BC的平面β,使得β⊥面ABC.可以發現圖(1)中A和D在β的異側,圖(2)中A和D在β的同側.也就是說二面角A-BC-D為鈍角?A和D在β的異側,二面角A-BC-D為銳角?A和D在β的同側.因此可以借助β來進行判斷.
在實際解題中,題目不可能出現β這樣的垂面,但是可以自行構造出來,如圖(3)所示.步驟如下:
1.建立空間直角坐標系,求出A,B,C的坐標.
2.求出面ABC的法向量
3.以公共棱BC的一個端點如B為起點,構造向量使得求出T點的坐標.此時垂直于面ABC.
4.以直線BT,BC為鄰邊作出一個平行四邊形,該平面必定與面ABC垂直,即為β.
當構造出了垂面β之后,如何借助β來進行判斷?

綜合上述分析,可以采用如下方法來判斷二面角A-BC-D是鈍角還是銳角:

例1.2015年安徽高考第19題如圖(5)所示,在多面體A1B1D1DCBA中,四邊形AA1B1B,ADD1A1,ABCD均為正方形,E為B1D1的中點,過A1,D,E的平面交CD1于F.(1)略.(2)求二面角E-A1D-B1余弦值.
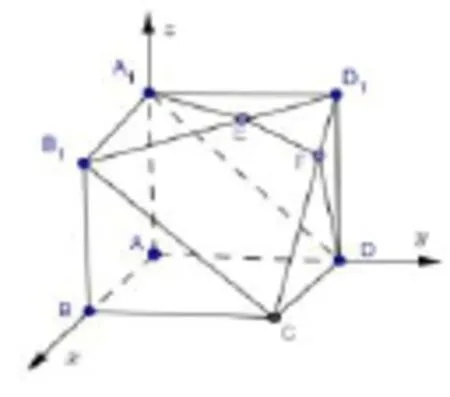
圖5

圖6


圖7
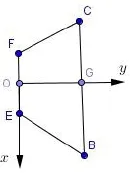
圖8
例2.2015年北京高考第17題如圖(7)所示,在四棱錐A-EFCB中,△AEF為等邊三角形,平面AEF⊥平面EFCB,EF//BC,BC=4,EF=2a,∠EBC=∠FCB= 60°,O為EF的中點.(1)略(2)求二面角F-AE-B的余弦值.(3)略.
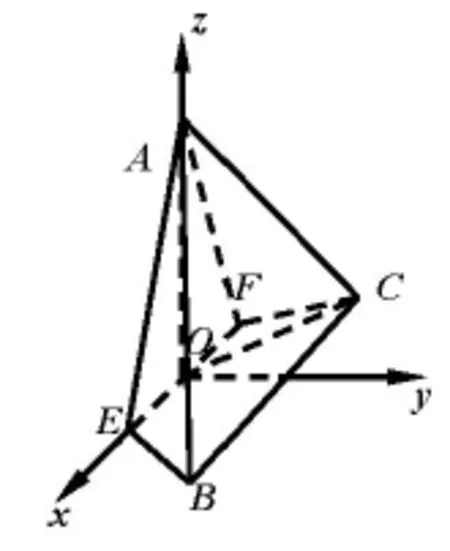
圖9

圖10

上述方法是從數學嚴謹的角度來判斷二面角是鈍角還是銳角.實際上對于利用坐標法求解二面角的題目,可以繞開這個難點直接求解.
二、利用直線的單向法向量
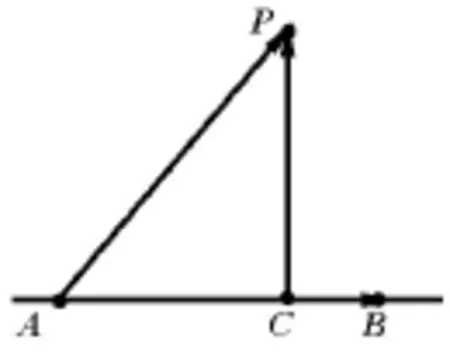
圖11
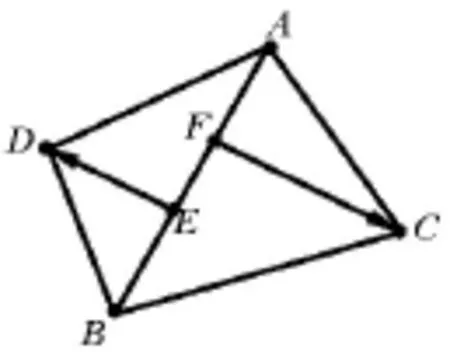
圖12
1.直線關于線外一點的單向法向量.
如圖(11)所示,在直線l上取兩點A,B,點P為直線外一點.作PC⊥l,垂足為C.則稱為直線AB關于點P的單向法向量.

2.如何利用單向法向量求二面角?

上述方法的優點在于避免了根據圖形判斷二面角是鈍角還是銳角.
例3.同例1


例4.同例2

結束語
本文所介紹方法的優點在于能夠用嚴格的數學符號語言代替直觀的圖形判斷,進一步可以避免這個判斷上的難點,也就是直接求出二面角的余弦值.本文方法來源于教材又高于教材,能夠較好地培養學生的分析能力,運算求解能力,拓展思維.雖然在計算上稍顯復雜,但是作為一種課后補充還是可取的.

