變精度T-粗糙集*
朱 熙 張惠玲 李 鑫
(西安航空學院理學院 西安 710077)
變精度T-粗糙集*
朱 熙 張惠玲 李 鑫
(西安航空學院理學院 西安 710077)
論文給出了變精度T-粗糙集的概念,并且研究了它的一些性質。討論了雙參數變精度T-粗糙集關于參數的變化情況。論文得到的結果從算子論和集合論的角度豐富了粗糙集的理論體系。
粗糙集; 集值映射; 變精度粗糙集; 變精度T-粗糙集
Class Number TP18
1 引言
粗糙集理論是20世紀80年代初Z.Pawlak[1]針對邊界域思想提出的。它是一種處理模糊和不確定性知識的數學工具,是人工智能中的一種重要推理技術。粗糙集的定義沒有充分利用邊界區域中的統計信息,為了研究這個問題,1993年Ziarko[2]通過引入一個β近似空間來反映這種限制,提出了變精度粗糙集模型。從此,許多學者對該模型進行了研究[3~6],主要集中在基于變精度粗糙集模型的知識約簡理論與方法、模型推廣及模型的應用[7~8]。變精度粗糙集模型繼承了經典粗糙集模型的所有基本數學特征,對集合包含運算進行了擴充,允許一定程度的錯誤分類率存在,從而具有對噪聲數據的適應能力,可以有效地分析不完備或不精確信息。
2 預備知識
定義1[9]設U是一個非空集合,θ是U上的等價關系,則稱序對(U,θ)為一個近似空間。
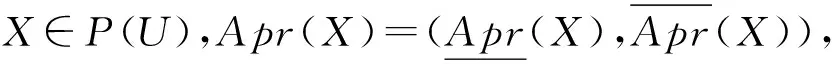
定義3[10]設X和Y是兩個非空集合且B?Y。設T:X→P*(Y)是一個集值映射,其中P*(Y)記為Y的所有非空子集的集合。則在T下B的下逆和上逆定義為
T-1(B)={x∈X|T(x)∩B≠?},
T+(B)={x∈X|T(x)?B}
命題1[10]設X和Y是兩個非空集合且T:X→P*(Y)是一個集值映射。如果A和B是Y的兩個非空集合,則以下成立:
1)T-1(A∩B)?T-1(A)∩T-1(B);
2)T-1(A∪B)=T-1(A)∪T-1(B);
3)T+(A∩B)=T+(A)∩T+(B);
4)T+(A)∪T+(B)?T+(A∩B);
5)A?B?T+(A)?T+(B);
6)A?B?T-1(A)?T-1(B)。
應用上逆和下逆,定義Y的子集的二元關系如下
A?B?T-1(A)=T-1(B)且T+(A)=T+(B)。
這個等價關系誘導出了P*(Y)的一個劃分P*(Y)/?,?的等價類稱為T-粗糙集。
3 變精度T-粗糙集
定義4 設X和Y是兩個非空集合且B?Y,β∈(0.5,1]。設T:X→P*(Y)是一個集值映射,其中P*(Y)記為Y的所有非空子集的集合。則在T下B的β下逆和β上逆定義為
例子1 設X={x,y,z,t},Y={a,b,c}。考慮集值函數T:X→P*(Y)定義為T(x)={b},T(y)={a,c},T(z)={b},T(t)={a,b,c}。設β=0.6,B={a,b},則
定理1 設X和Y是兩個非空集合且T:X→P*(Y)是一個集值映射,則以下成立:






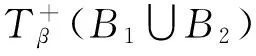


={x∈X|T(x)≠?}
={x∈X|T(x)≠?}





7) 證明方法過程類似6)。



4 雙參數變精度T-粗糙集
定義5 設X和Y是兩個非空集合且B?Y,0.5<β≤α≤1。設T:X→P*(Y)是一個集值映射,其中P*(Y)記為Y的所有非空子集的集合。則在T下B的β下逆和α上逆定義為
定理2 設X和Y是兩個非空集合且B?Y,T:X→P*(Y)是一個集值映射,其中P*(Y)記為Y的所有非空子集的集合。若0.5<α1≤α2≤1,0.5<β1≤β2≤1,則


定理2(1)表明兩個參數的變精度T-粗糙集的β下逆關于參數β是遞增的,定理2(2)表明兩個參數的變精度T-粗糙集的α上逆關于參數α是遞減的。
定理3 設X和Y是兩個非空集合且B?Y,0.5<β≤α≤1。設T:X→P*(Y)是一個集值映射,其中P*(Y)記為Y的所有非空子集的集合。則
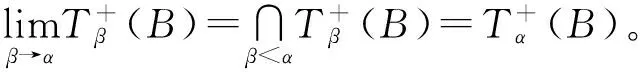
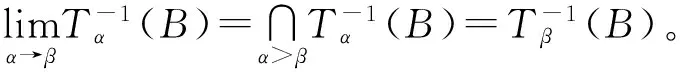
[1] Z. Pawlak. Rough sets[J]. Int. J. Inform. Comput. Sci.,1982,11(5):341-356.
[2] W. Ziarko. Variable precision rough set model[J]. Journal of Computer and System Sciences,1993,46(1):39-59.
[3] 張賢勇,莫智文.變精度粗糙集[J].模糊識別與人工智能,2004,17(2):151-155. ZHANG Xianyong, MO Zhiwen. variable precision rough sets[J]. Pattem Recognition and Aitificial Intelligence,2004,17(2):151-155.
[4] 高陽,鐘波.基于限制相似關系的變精度粗糙集模型[J].系統工程與電子技術,2009,31(7):1639-1641. GAO Yang, ZHONG Bo. Variable precision rough set model based on restricted similarity relation[J]. System engineering and electronic technology,2009,31(7):1639-1641.
[5] 姚燕青,米據生,李舟軍.一種新的基于模糊顆粒的變精度(θ,σ)-模糊粗糙集模型[J].模糊集與系統,2014,236:58-72. Y. Q. Yao, J. S. Mi, Z. J. Li. A novel variable precision (θ,σ)-fuzzy rough set model based on fuzzy granules[J]. Fuzzy Sets and Systems,2014,236:58-72.
[6] 曾雪蘭,梅良才,陳勝,等.IIS中基于限制容差關系的變精度粗糙集模型[J].廣西大學學報:自然科學版,2009,34(6):819-822. ZENG Xuelan. MEI Liangcai, CHEN Sheng, et al. Variable precision rough set model based on limited tolerance relation in IIS[J]. Journal of Guangxi University: Natural Science Edition,2009,34(6):819-822.
[7] 米據生,吳偉志,張文修.基于變精度粗糙集理論的知識約簡方法[J].系統工程理論與實踐,2004,24(1):76-82. MI Jusheng, WU Weizhi, ZHANG Wenxiu. Method of knowledge reduction based on Variable Precision Rough Set Theory[J]. System engineering theory and Practice,2004,24(1):76-82.
[8] 程玉勝,張佑生,胡學鋼.基于變精度粗集模型的變精度值自主式獲取方法[J].系統仿真學報,2007,11:2555-2558. CHENG Yusheng, ZHANG Yousheng, HU Xuegang. Variable precision value autonomous acquisition method based on Variable Precision Rough Set Model[J]. Journal of system simulation,2007,11:2555-2558.
[9] B. Davvaz. Roughness in rings[J]. Information Sciences,2004,164:147-163.
[10] B. Davvaz. A short note on algebraic T-rough sets[J]. Information Sciences,2008,178:3247-3252.
Variable Precision T-rough Sets
ZHU Xi ZHANG Huiling LI Xin
(College of Science, Xi’an Aeronautical University, Xi’an 710077)
In this paper, the concept of variable precision T-rough sets is given, and some properties of it are studied. The changes about parameter of double parametes variable precision T-rough sets are investigated. The theoretical system of rough set has been enriched by the results obtained in this paper from operator theory and set theory point of views.
rough sets, set-valued mapping, variable precision rough sets, variable precision T-rough sets
2016年9月11日,
2016年10月17日
西安航空學院科研基金(編號:2016GJ1004)資助。 作者簡介:朱熙,男,碩士,講師,研究方向:模糊數學。
TP18
10.3969/j.issn.1672-9722.2017.03.003

