周期性壓力作用下單層冪律流底泥流場(chǎng)分布
劉潔,白玉川
(天津大學(xué) 水利工程仿真與安全國(guó)家重點(diǎn)實(shí)驗(yàn)室,天津 300072)
周期性壓力作用下單層冪律流底泥流場(chǎng)分布
劉潔,白玉川
(天津大學(xué) 水利工程仿真與安全國(guó)家重點(diǎn)實(shí)驗(yàn)室,天津 300072)
基于歐拉坐標(biāo)系統(tǒng),對(duì)河口底泥流場(chǎng)分布進(jìn)行了理論研究。泥波由作用在其表面的周期性壓力驅(qū)動(dòng),底泥的流變特性由冪律流流變模型描述,根據(jù)淺水波和小變形假設(shè),采用攝動(dòng)分析展開到一階得到運(yùn)動(dòng)方程,并且用數(shù)值迭代法求解非線性微分方程。根據(jù)數(shù)值計(jì)算結(jié)果,分析冪律流流動(dòng)指數(shù)和外加周期性壓力載荷對(duì)泥波流場(chǎng)分布和表面波高的影響。
底泥;冪律流模型;周期性壓力;流場(chǎng);波高
在我國(guó)長(zhǎng)長(zhǎng)的海岸線上淤泥質(zhì)海岸線超過4 000 km。淤泥質(zhì)海岸多地勢(shì)平坦,是多種魚類、貝類等生物以及藻類植物賴以生存的場(chǎng)所(劉曉收等,2014),是海洋濕地生態(tài)的重要組成部分;而各河口淤泥質(zhì)海岸又存在不同程度的泥沙淤積問題(閆龍浩等,2010);加之深水航道的建設(shè),使得河口淤泥質(zhì)粘性泥沙的研究遇到新的挑戰(zhàn)。由于受到水流、波浪和潮汐等多種因素影響,河口處的水動(dòng)力環(huán)境異常復(fù)雜。其中,波浪與底泥之間的相互作用引起的泥波流場(chǎng)分布變化和波浪衰減受到學(xué)者的廣泛關(guān)注。
研究波浪與底泥之間的相互作用時(shí),上層流體和下層淤泥質(zhì)底泥的流變特性一般由不同的流變模型描述。最早,Grade(1958)將上層水體假設(shè)為理想流體,下層底泥假設(shè)為粘性流體,建立了淺水條件下的兩層流體模型;Dalrymple等(1978)考慮了上層水體的粘性,將上下兩層都假設(shè)為粘性流體,建立起兩層互不摻混的粘性流體模型;Ng(2004)根據(jù)邊界層理論,將波浪與底泥均假設(shè)為粘性流體進(jìn)行了研究;Ng(2004)還采用一種冪律流流變模型對(duì)底泥進(jìn)行描述。另外一些研究考慮了底泥的固體特性,將底泥假設(shè)為粘彈性模型(趙子丹等1997;Ng,2002;牛小靜等,2008)或者粘塑性模型(Becker et al,2000;Zhang,2006;Xia,2010;Xia,2011)。此外,還有一些研究同時(shí)考慮了底泥具有彈塑性,用粘彈塑性模型(牛小靜等,2008)描述底泥的流變性質(zhì)。
海岸床面底泥具有非牛頓流體特性,表現(xiàn)出典型的剪切稀化性質(zhì),即粘度隨著剪切率的增大而減小。而底泥的這種性質(zhì)可以由賓漢塑性體模型很好的描述,所以應(yīng)用最為廣泛。但是在理論研究中,瞬態(tài)理論很難確定賓漢塑性體模型的屈服位置,必須作為問題的一部分在計(jì)算中求解。因此,本文采用一種更加方便實(shí)用的流變模型,即冪律流模型。通過對(duì)天津海河口淤泥(白玉川等,2011)和連云港徐圩試挖槽浮泥(白玉川等,2011)的流變?cè)囼?yàn)研究,發(fā)現(xiàn)冪律流模型可以很好地描述底泥的非線性流變特性,尤其是在低剪切率時(shí)(5-50s-1)。
本文在考慮淤泥質(zhì)底泥非線性特性的基礎(chǔ)上建立理論模型,對(duì)冪律流泥流的泥波流場(chǎng)分布進(jìn)行初步研究。不同于傳統(tǒng)的兩層或者多層模型,為了簡(jiǎn)化數(shù)學(xué)模型,本文假設(shè)只有單層高濃度的淤泥存在;為了反映波浪與淤泥質(zhì)底泥之間的相互作用,直接在淤泥質(zhì)泥流表面作用周期性壓力,類似的假設(shè)在Becker等(2001)研究波浪與底泥之間的相互作用中被采用。
1 理論模型與方法
1.1基本假設(shè)與公式
假設(shè)在水平的剛性床面上存在一層均勻的底泥,深度為h。底泥為不可壓縮的各向同性體,密度為ρ,且沿x軸方向無限長(zhǎng),高濃度泥流用冪律流流變模型描述。為驅(qū)使底泥運(yùn)動(dòng),外加壓力直接作用在泥層表面,其形式為時(shí)間和空間的周期性函數(shù),表達(dá)式類似行進(jìn)波:P=Pscos(kx-σt);其中,Ps為壓力幅值,k為波數(shù),σ為角頻率。泥波沿x軸的正方向傳播,淤泥層底部固定在z=-h處;表面位置由η=z(x,0,t)表示,如圖1所示。
x-z平面內(nèi)的運(yùn)動(dòng)方程包括連續(xù)性方程、水平方向和垂直方向的動(dòng)量方程


圖1 泥波傳播幾何示意圖

其中,u和w分別為沿x方向的水平速度和沿z方向的垂直速度,g為重力加速度。
如前所述,中國(guó)大多數(shù)河口海岸淤泥質(zhì)底泥的流變特性可以由冪律流模型描述,而冪律流的流變關(guān)系(Ng,2004;白玉川等,2011)可以表示為


γ˙為剪切應(yīng)力幅值,大小為

所以,各應(yīng)力分量與剪切應(yīng)力幅值可以表示成
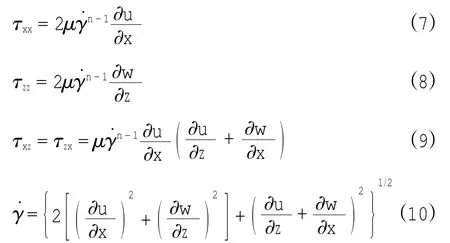
為了使方程完整,需要邊界條件。首先,引入切應(yīng)力T和正應(yīng)力N表達(dá)式
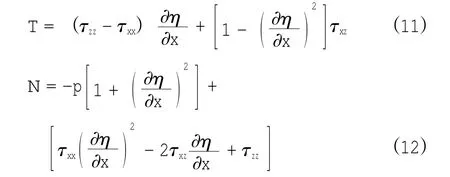
自由表面(z=0)處的動(dòng)力學(xué)邊界條件包括:切應(yīng)力T為0,而正應(yīng)力N等于外加壓力載荷

自由表面(z=0)處的運(yùn)動(dòng)學(xué)邊界條件為:法向速度為零

底部(z=-h)邊界條件為水平速度和垂直速度均為零

1.2無量綱化
本文的一個(gè)重要假設(shè)是泥層厚度h遠(yuǎn)小于波長(zhǎng)L,即h< 其中,F(xiàn)r為弗勞德數(shù);λ2為Stoke’s邊界層厚度的平方與泥流厚度h的平方之比。 應(yīng)力分量和剪切應(yīng)力幅值的無量綱形式為 將式(33)帶入無量綱運(yùn)動(dòng)方程式(19)-(21)和邊界條件式(28)-(32),取其中一階變量,就得到一階問題的運(yùn)動(dòng)方程和邊界條件。 一階問題的連續(xù)性方程和動(dòng)量方程分別為 其中,剪切分量 泥面波位移為 將式(37)和(43)帶入式(35),得到如下一階問題的控制方程 很顯然,控制方程(45)為非線性微分方程,只有當(dāng)流動(dòng)指數(shù)n=1.0時(shí),可以得到解析解。所以采用數(shù)值迭代法求解式(45),求解為范圍0≤ 首先,式(45)可以寫成如下隱式迭代格式 其中,uk表示第k步迭代,為已知量。uk+1為第k+1步迭代,為待求解未知量。 在網(wǎng)格結(jié)點(diǎn)(i,j)處,各變量的一階和二階中心差分格式為 將式(48)帶入式(47),得到一階控制方程的離散形式 圖2 網(wǎng)格剖分示意圖 自由表面(i=1,2,…,N,j=N)邊界條件的離散形式為 底部床面(i=1,2,…,N,j=1)邊界條件式的離散形式為 用數(shù)值迭代法求解時(shí)要輸入以下幾個(gè)參數(shù):n,λ2,F(xiàn)r和Ps。為了節(jié)省計(jì)算工作量,將流體為牛頓體(即n=1.0)時(shí)得到的u的解析解(Ng 2004)作為數(shù)值求解的初始值,求解得到n=0.9時(shí)的u值;并將n=0.9的解作為求解n=0.8時(shí)u的初值。以此類推,求解得到n=0.7、0.6、…、0.3時(shí)的數(shù)值解。當(dāng)兩次迭代之間的最大差值的絕對(duì)值差值小于10-4時(shí),數(shù)值計(jì)算結(jié)束。文中其他參數(shù)值的設(shè)置分別為:λ2=Fr=1.0、Ps=1.0和Ps=2.0。為驗(yàn)證程序代碼的正確性,對(duì)比n=1.0時(shí)的數(shù)值計(jì)算結(jié)果和假設(shè)流體為牛頓體時(shí)求解得到的解析解結(jié)果,如圖3所示。 由圖3可知,n=1.0時(shí)的數(shù)值解的流場(chǎng)分布與流體為牛頓流體時(shí)解析解的流場(chǎng)分布一致,從而證明了本文程序代碼的正確性。當(dāng)流體為牛頓體時(shí),二維流場(chǎng)為簡(jiǎn)單簡(jiǎn)諧運(yùn)動(dòng),水平速度u和垂向速度w為相位ξ的簡(jiǎn)諧函數(shù)。在表面周期性壓力作用下,一個(gè)周期內(nèi)的垂向速度w隨壓力梯度的變化遵循余弦函數(shù)變化:在相位ξ=0處,垂向速度w達(dá)到正的最大值,在相位ξ=π處達(dá)到負(fù)的最大值;而在相位ξ=π/2和3π/2處,垂向速度等于0。 圖3 牛頓流體解析解結(jié)果二維流場(chǎng)矢量圖 隨冪律流流動(dòng)指數(shù)n減小,二維流場(chǎng)分布如圖4所示。由圖可知,當(dāng)載荷Ps=1.0,隨著n值減小,泥流的非牛頓體特性越明顯,雖然流場(chǎng)依然表現(xiàn)出周期性,但隨著相位ξ變化,流場(chǎng)已經(jīng)不再是簡(jiǎn)單的簡(jiǎn)弦變化;而且隨冪律流流動(dòng)指數(shù)減小的值增大,流場(chǎng)的變化越明顯。此外,當(dāng)冪律流流動(dòng)指數(shù)n減小到一定值后,在ξ=0和π附近,由于作用力很小,出現(xiàn)流動(dòng)靜止?fàn)顟B(tài),這種現(xiàn)象可以由剪切稀化現(xiàn)象解釋。 圖4 二維流場(chǎng)隨冪律泥流流動(dòng)指數(shù)變化的分布圖 當(dāng)載荷增加到Ps=2.0,隨冪律流流動(dòng)指數(shù)n減小,二維流場(chǎng)分布如圖5所示。由圖可知,當(dāng)自由表面所施加的壓力載荷從1.0增加到2.0時(shí),二維流場(chǎng)在一個(gè)周期內(nèi)仍然表現(xiàn)出周期性變化,而且最大速度值遠(yuǎn)大于Ps=1.0時(shí)。但是,隨著流動(dòng)指數(shù)nm減小,流場(chǎng)變化較Ps=1.0時(shí)并不顯著。這是因?yàn)楫?dāng)外加載荷增大到一定值后,作用力對(duì)于泥波的影響大于泥流粘性對(duì)泥波運(yùn)動(dòng)的影響。同時(shí),在ξ=0和π附近,由于作用力增大,流動(dòng)靜止現(xiàn)象也隨之消失。 圖6為一個(gè)周期內(nèi),波高隨流動(dòng)指數(shù)n變化的示意圖。其中,圖6(a)為Ps=1.0,圖6(b)為Ps=2.0。由圖可知,不同壓力載荷作用下,波高均隨流動(dòng)指數(shù)n減小而減小。 當(dāng)Ps等于1.0時(shí),波高在ξ=π/2時(shí)達(dá)到正的最大值,即為波峰;而在ξ=3π/2時(shí),波高到達(dá)負(fù)的最大值,即為波谷。隨著流動(dòng)指數(shù)越小,因?yàn)槟嗔鞯恼承栽矫黠@,驅(qū)動(dòng)泥流運(yùn)動(dòng)所需得作用力就越大,圖中表現(xiàn)為:n=1.0時(shí)的波高約為n=0.3時(shí)波高的兩倍;然而當(dāng)n從1.0減小到0.7時(shí),波高變化并不明顯,減小量小于1/5。 而當(dāng)Ps增大到2.0時(shí),流動(dòng)指數(shù)n從1.0減小到0.3時(shí),波高的減小幅度并不明顯。這是因?yàn)楫?dāng)外加載荷增大到一定值后,作用力對(duì)于泥波運(yùn)動(dòng)的影響大于泥流粘性對(duì)運(yùn)動(dòng)的影響。此外,圖6(a)更直觀證明了圖4中當(dāng)n=0.3出現(xiàn)的流動(dòng)靜止現(xiàn)象,即在ξ=0和π附近流動(dòng)出現(xiàn)間歇性停止。 本文基于歐拉坐標(biāo)系統(tǒng),介紹了一種攝動(dòng)理論,初步研究了表面周期性壓力作用下單層冪律流底泥的流場(chǎng)分布。主要得到以下結(jié)果: 圖5 二維流場(chǎng)隨冪律泥流流動(dòng)指數(shù)變化的分布圖 圖6 波高隨冪律流泥流流動(dòng)指數(shù)變化示意圖 當(dāng)外加載荷等于1.0時(shí),隨冪律流流動(dòng)指數(shù)n逐漸減小,二維流場(chǎng)雖然依然表現(xiàn)出周期性,但是已經(jīng)不再是簡(jiǎn)單的簡(jiǎn)諧函數(shù)。而且,當(dāng)流動(dòng)指數(shù)減小到一定值時(shí),會(huì)出現(xiàn)流動(dòng)間歇性停止,這是因?yàn)楹涌诘啄嗑哂屑羟邢』再|(zhì)。 當(dāng)外加載荷增大到2.0時(shí),由于作用力對(duì)泥波運(yùn)動(dòng)的影響大于泥流粘性對(duì)其的影響,所以冪律流流動(dòng)指數(shù)的減小對(duì)于二維流場(chǎng)的影響減弱,流動(dòng)停止現(xiàn)象也隨之消失。 然而,本文僅是對(duì)周期性載荷作用下泥流的流場(chǎng)分布進(jìn)行了研究,這是研究波浪和底泥之間相互作用的第一步。后續(xù)工作希望基于兩層波浪與底泥相互作用的數(shù)學(xué)模型,考慮二階響應(yīng),研究?jī)缏闪髁鲃?dòng)指數(shù)和外加載荷對(duì)于流場(chǎng)和質(zhì)量輸移的影響。 Becker J M,Bercovici D,2000.Permanent bedforms in a theoretical model of wave-sea-bed interactions.Nonlinear Processes in Geophysics,201(7):31-35. Becker J M,Bercovici D,2001.Pattern formation on the interface of a two-layer fluid:bi-viscous lower layer.Wave Motion,34(1): 431-452. Dalrymple R A,Philip L F,1978.Waves over soft muds:a two layer model.Journal of Physical Oceanography,8(7):1121-1131. Gade H G,1958.Effects of a non-rigid impermeable bottom on plane surface waves in shallow water.Journal of Marine Research,16(3):61-82. Ng C O,2004.Mass transport in gravity waves revisited.Journal of Geophysical Research,109(12):1-13. Ng C O,2004.Mass transport in a layer of power-law fluid forced by periodic surface pressure.Wave Motion,39(3):241-259. Ng C O,Bai Y C,2002.Mass transport in a thin layer of Bi-Viscous mud under surface waves.China Ocean Engineering,16(4):423-436. Xia Y Z,Zhu K Q,2010.A study of wave attenuation over a Maxwell model of a muddy bottom.Wave Motion,47(8):601-615. Xia Y Z,Zhu K Q,2011.On a fractional-order Maxwell model of seabed mud and its effect to surface wave damping.Applied Mathematics and Mechanics,32(11):1357-1366. Zhang X Y,Ng C O,2006.Mud-wave interaction:a viscoelastic model.China Ocean Engineering,20(1):15-26. 劉曉收,趙瑞,華爾,等,2014.萊州灣夏季大型底棲動(dòng)物群落結(jié)構(gòu)特征及其與歷史資料的比較.海洋通報(bào),33(3):283-292. 牛小靜,余錫平,2008.復(fù)雜粘彈性流體運(yùn)動(dòng)的數(shù)值計(jì)算方法.水動(dòng)力學(xué)研究與進(jìn)展A輯,23(3):331-337. 牛小靜,余錫平,2008.泥質(zhì)海床的粘彈性模型.清華大學(xué)學(xué)報(bào)(自然科學(xué)版),48(9) :1417-1421. 龐啟秀,2011.浮泥形成和運(yùn)動(dòng)特性及其應(yīng)對(duì)措施研究.天津大學(xué).博士學(xué)位論文. 田琦,白玉川,2011.不同流變模型下的淤泥與波浪相互作用規(guī)律.天津大學(xué)學(xué)報(bào),44(3):196-201. 閆龍浩,楊世倫,李鵬,等,2010.近期(2000-2008年)長(zhǎng)江口南港河槽的沖淤變化——兼議外高橋新港區(qū)岸段強(qiáng)烈沖淤原因.海洋通報(bào),29(4):378-384. 趙子丹,劉同利,1997.淤泥流變參數(shù)的確定.海洋通報(bào),16(5):71-78. (本文編輯:袁澤軼) Flow field distribution in a layer of power-law muddy fluid forced by the periodic pressure LIU Jie,BAI Yu-chuan (State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China) Based on an Eulerian coordinate system, a theoretical research is presented for the flow field of muddy fluid which is forced by a periodic pressure on the free surface.The muddy fluid has a thin layer, which is described by a powerlaw model.By the assumption of shallowness and deformation, a perturbation analysis is carried out to the first order.The numerical iteration method is adopted to solve these non-linear equations.For the different fluid indices and pressure loads,both the flow field and wave height are examined. bed mud; power-law model; periodic pressure load; flow field; wave height P731.2 A 1001-6932(2017)01-0052-08 10.11840/j.issn.1001-6392.2017.01.007 2015-10-13; 2015-12-16 國(guó)家自然科學(xué)基金 (40376028);天津市應(yīng)用基礎(chǔ)研究計(jì)劃(11JCYBJC03200)。 劉潔 (1986-),女,博士生,主要從事河口海岸淤泥特性和底泥質(zhì)量輸移研究。電子郵箱:liujie.mars@tju.edu.cn。 白玉川,男,教授。電子郵箱:ychbai@tju.edu.cn。




2 攝動(dòng)分析







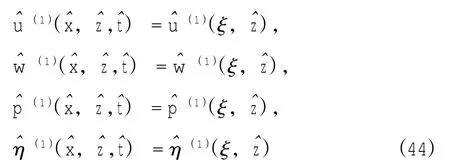


3 數(shù)值求解及結(jié)果分析








4 結(jié)論



