雙組分氣體自發凝結成核模型修正

楊 文，侯志強，陳 鵬，曹學文

(1.中國石化銷售有限公司 華南分公司管道技術中心， 廣東 廣州 510620； 2.中國石油化工股份有限公司工程部， 北京 100728；3.中國石油西氣東輸管道公司(西氣東輸銷售公司) 鄭州管理處， 河南 鄭州 450000； 4.中國石油大學 儲運與建筑工程學院， 山東 青島 266580)

雙組分氣體自發凝結成核模型修正

楊 文1，侯志強2，陳 鵬3，曹學文4

(1.中國石化銷售有限公司 華南分公司管道技術中心， 廣東 廣州 510620； 2.中國石油化工股份有限公司工程部， 北京 100728；3.中國石油西氣東輸管道公司(西氣東輸銷售公司) 鄭州管理處， 河南 鄭州 450000； 4.中國石油大學 儲運與建筑工程學院， 山東 青島 266580)

針對雙組分氣體自發凝結經典成核模型及Looijmans修正的經典成核模型存在未考慮真實氣體效應或考慮真實氣體效應時化學勢差計算復雜、成核動力項生長速率向量中碰撞率的計算采用了理想氣體的表達形式、未考慮液滴曲率半徑對表面張力的影響的缺點，對雙組分氣體自發凝結成核模型進行了修正。將以上缺點均修正的修正模型1的計算結果與實驗數據的偏差較大，最小偏差仍大于2個數量級，認為是不準確的液滴表面張力模型的引入造成的結果。僅考慮真實氣體效應修正和碰撞率計算修正的修正模型2較修正模型1的計算結果更為接近實驗值，誤差可在2個數量級以內。修正模型2對不同介質雙組分氣體自發凝結成核預測值較Looijmans模型預測值更接近實驗值，且大部分情況下較Kalikmanov提出的半現象學理論模型更為準確，推薦使用修正模型2進行雙組分氣體自發凝結成核率預測。

雙組分； 凝結； 狀態方程； 氣液平衡； 實驗驗證

超聲速旋流分離器因結構緊湊、穩定性好(無轉動部件)、無需添加化學藥劑、節能環保等優點，在天然氣處理加工過程中得到了推廣應用[1-2]。中國石油大學[3-8]、大連理工大學[9-12]、北京工業大學[13-16]開展了旋流分離器在脫水、脫重烴等方面的研究工作，曹學文等[17-18]更將其推廣應用于天然氣液化過程中。

氣體在超聲速旋流分離器內的凝結、分離流動過程是超聲速旋流分離技術的關鍵。國內學者雖開展了相應的研究，但對于凝結模型的準確性卻較少關注，均采用了現有凝結模型，即經典成核理論模型；且均主要關注單組分的凝結過程，對于雙組分或多組分的凝結關注較少。用以描述雙組分氣體自發凝結成核過程的理論包括經典成核理論及半唯象學理論。Flood[19]與Volmer[20]分別于1934年和1939年基于等分子波動理論提出了最初的單組分成核理論；在此基礎上，Reiss[21]于1950年將單組分經典成核理論擴展應用于雙組分體系，形成了后來所稱的雙組分體系經典成核理論(Binary classical nucleation theory，BCNT)。關于雙組分體系凝結成核特性研究較少，Looijmans等[22-23]進行了少量相關研究，在Wilemski形成自由能計算及Stauffer成核動力項計算的基礎上，引入真實氣體效應，形成了考慮真實氣體效應的雙組分體系經典成核理論。但所提出模型仍存在一定的缺點。化學勢差的計算存在復雜的微積分過程；在成核動力項中，生長速率向量中碰撞率的計算采用了理想氣體的表達形式，模型存在不一致性；采用了Macleod-Sugden關聯式計算混合液相表面張力，未考慮液滴半徑對表面張力的影響。

筆者在BCNT模型及Looijmans模型的基礎上，考慮了真實氣體效應、碰撞率計算及液滴曲率半徑對表面張力的影響，推導出了改進的成核率計算模型，并采用成核率實驗數據對模型計算結果進行了驗證分析。

1 經典成核率模型存在的問題

雙組分氣體體系自發凝結成核率公式如式(1)所示。其中，動力前因子K由式(2)計算。

JBCNT=K·e-ΔG*/kBT

(1)

K=RavZN

(2)

式(2)中，平均生長速率Rav由式(3)求解，而式(3)中的二維生長速率張量R由式(4)求解。

Rav=det(R)/(R11sin2φ+R22cos2φ-2R12sinφcosφ)

(3)

(4)

對雙組分體系，只考慮單個分子與(n1,n2)體系的碰撞聚結，因此生長速率張量元素可表達為式(5)～(7)。其中單個分子與分子團碰撞率β可由式(8)求解。

R11=β1A(n1,n2)

(5)

R12=R21=0

(6)

R22=β2A(n1,n2)

(7)

(8)

Zeldovich因子Z可由式(12)求解，其中自由能二階偏導數的張量D可由式(9)計算[22]。

(9)

Wilemski[24-25]依據于其所提出的液滴模型，即認為液滴內部與液滴表面達到熱力學平衡，液滴表面分子層對液滴體積無貢獻，于1984年提出了雙組分氣體凝結成核自由能計算模型式(10)。

(10)

雙組分氣體凝結液滴形成自由能是組分1與組分2分子數的函數，其函數圖形為一鞍形曲面，該曲面鞍點即為臨界成核液滴所需的形成自由能，其所對應的分子數即為臨界液滴中組分1與組分2分子數。鞍點自由能由式(11)確定。

(11)

結合Gibbs-Duhem關系式、液滴表面Gibbs adsorption方程、Laplace方程及流體的不可壓縮性假設，得到Kelvin方程式(12)。其中的*μi由式(13)計算。

(12)

Δ*μi=μli(pv,T)-μvi(pv,T)

(13)

鞍點處Δμi=0，由式(11)得到鞍點處Gibbs形成自由能如式(14)所示。

(14)

Looijmans等修正的經典成核模型[26]中采用了應用較為廣泛、精確度較好的Macleod & Sugden關聯式計算液滴表面張力σ，如式(15)所示。對于烴類體系，n取為4

σm0={[Plm]ρlm-[Pvm]ρvm}n

(15)

對于式(13)中化學勢差的求解，經典成核理論中采用了理想氣體假設，即得到式(16)。

Δ*μi=-kBTlnSi

(16)

Looijmans等[23]考慮真實氣體效應的影響，形成了考慮真實氣體效應的雙組分體系經典成核理論，但化學勢差的計算存在復雜的微積分過程。

從上述分析過程可以看出，雙組分經典成核理論計算模型存在以下3個需要改進的地方。

(1)氣體凝結時一般已偏離理想氣體狀態，而模型中均為考慮真實氣體對于成核的影響，但仍采用理想氣體假設求解化學勢差，從而將理想氣體假設引入至成核率計算模型中。Looijmans修正模型中引入了真實氣體效應的影響，但計算過程存在復雜的微積分過程。

(2)在成核動力項中，生長速率向量中碰撞率采用了理想氣體的表達式來計算，Looijmans模型中也仍沿用了此計算形式，使得模型存在不一致性。

(3)氣體發生凝結時，其氣-液相界面并非平面，而是高度彎曲的曲面。所凝結的液滴表面自由能取決于表面張力和表面積的大小，它抵抗著液滴的生長，故而表面張力的大小對凝結特性有較大的影響。但模型中未考慮到液滴彎曲曲面對于成核的影響。

因此，在本研究中從以上3個方面對成核率計算模型進行了修正。

2 成核率模型的修正

2.1 化學勢差計算方法修正

考慮真實氣體效應，引入逸度計算化學勢差。該計算方法既簡化了計算過程，又不存在任何簡化忽略。

對于達到平衡的兩相，分別采用逸度來表達兩相的化學勢，如式(17)、(18)所示。兩個標準態間存在嚴格的關系式(19)。

(17)

(18)

(19)

結合式(17)～(19)可得到氣-液相間化學勢差，如式(20)所示。

(20)

式(20)中的氣相及液相的逸度采用真實氣體狀態方程計算，所采用的狀態方程包括SRK方程、PR方程、PRSV方程、PRSV2方程及PT方程。

同時，還應注意到Kelvin方程中偏分子體積的計算，也應采用真實氣體狀態方程，如式(21)、(22)所示。

(21)

(22)

當采用SRK方程進行液相摩爾體積計算時，采用Peneloux模型計算c1、c2；采用其他真實氣體狀態方程進行液相摩爾體積計算時，c1、c2取為0。

2.2 碰撞率計算修正

為簡化計算，經典成核速率計算模型及Looijmans模型均采用了理想氣體假設，利用理想氣體狀態方程計算分壓，造成了計算結果的不準確性，如式(23)所示。

(23)

逸度在化學熱力學中表示實際氣體的有效壓力，筆者為將真實氣體效應引入碰撞率計算過程中，采用各組分逸度代替分壓進行碰撞率的計算，式(23)改寫為式(24)。

(24)

2.3 液滴表面張力修正

平面的表面張力來自表面上液體分子所受到的不平衡力，微小液滴彎曲表面上與平面上表面分子所受的不平衡力不可能一樣。因此，用平面的表面張力代替微小液滴的表面張力的計算結果并不可靠。Tolman[27-28]、Benson和Shuttleworth[29]曾對這個問題進行過熱力學分析，建立了液滴表面張力計算模型。

黃躍[30]、Campbell等[31-32]研究結果表明，Benson & Shuttleworth模型(簡稱BS模型)較Tolman模型更為準確；同時，Tolman模型中δ參數為一范圍值，選取存在人為因素。因此，筆者采用BS模型考慮液滴半徑對液滴表面張力的影響，將其引入成核率計算模型中。BS模型如式(25)所示。

(25)

3 成核率修正模型的實驗結果驗證

3.1 模型修正1的結果討論

依據上述對模型所作修正，所得修正模型簡稱為修正模型1，結合MATLAB軟件，編制成核率計算程序，將甲烷+壬烷雙組分、甲烷+辛烷雙組分烴類氣體成核率計算結果與實驗數據進行對比，以驗證模型的準確性及適用性。以計算結果與實驗結果偏差數量級(lg(Jcal/Jexp))為衡量指標，以 Looijmans[22]利用消光法所測得的實驗數據進行對比分析。

圖1為不同溫度下雙組分體系成核率修正模型1計算與實驗結果誤差分析。從圖1可以看出，修正模型1利用SRK和PT方程進行化學勢差計算時，計算結果與實驗結果偏差較小，但最小偏差也大于2個數量級；采用其余真實氣體狀態方程進行計算時，最大誤差可達19個數量級。可以看出，對于雙組分氣體體系，修正模型計算結果與實驗結果偏差較大。

圖1 雙組分體系成核率修正模型1計算結果與實驗結果對比分析Fig.1 Comparison of calculated results by modified model 1 and experimental results of nucleation rate in binary vapor system(a) Methane and nonane, 250 K； (b) Methane and nonane, 240 K； (c) Methane and nonane, 230 K； (d) Methane and octane, 240 K

3.2 修正模型2適應性分析

筆者認為，采用修正模型1造成如此大的計算誤差有可能是因為液滴表面張力模型的引入。為驗證此想法，模型修正時不考慮液滴曲率半徑對表面張力的影響，所得修正模型簡稱為修正模型2。

仍采用上述實驗數據，分析修正模型2的適應性， 結果示于圖2。從圖2可以看出，采用PR、PRSV、PRSV2進行化學勢差計算時，誤差仍較大，最大可達15個數量級，但小于修正模型1的19個數量級計算誤差；利用SRK、PT方程計算時，誤差較小，尤其是SRK方程，誤差均在2個數量級以內，較修正模型1的大于2個數量級的計算誤差取得了更好的預測結果。因此，推薦使用修正模型2進行雙組分氣體凝結成核預測。

3.3 修正模型2與其他模型計算結果對比

為進一步驗證采用SRK方程計算化學勢差的修正模型2的準確性，將計算結果與Looijmans修正的經典成核理論模型、Kalikmanov提出的半現象學理論模型(QOC)計算結果進行對比分析，結果示于圖3、4。Looijmans修正的經典成核理論模型在修正過程中化學勢差的計算存在復雜的微積分過程；且同時，在成核動力項中，生長速率向量中沖擊速率的計算采用了理想氣體的表達形式，模型存在不一致性。QOC模型中多處推導過程中采用了理想氣體假設。從圖3、4可以看出，修正模型2的計算結果均好于Looijmans修正模型，大部分情況下好于半唯象學理論模型，僅在甲烷+壬烷體系中230 K-1 MPa 及甲烷+辛烷體系240 K-2 MPa的計算結果略遜于半現象學理論模型計算結果。因此，筆者所提出模型具有較好的預測效果。

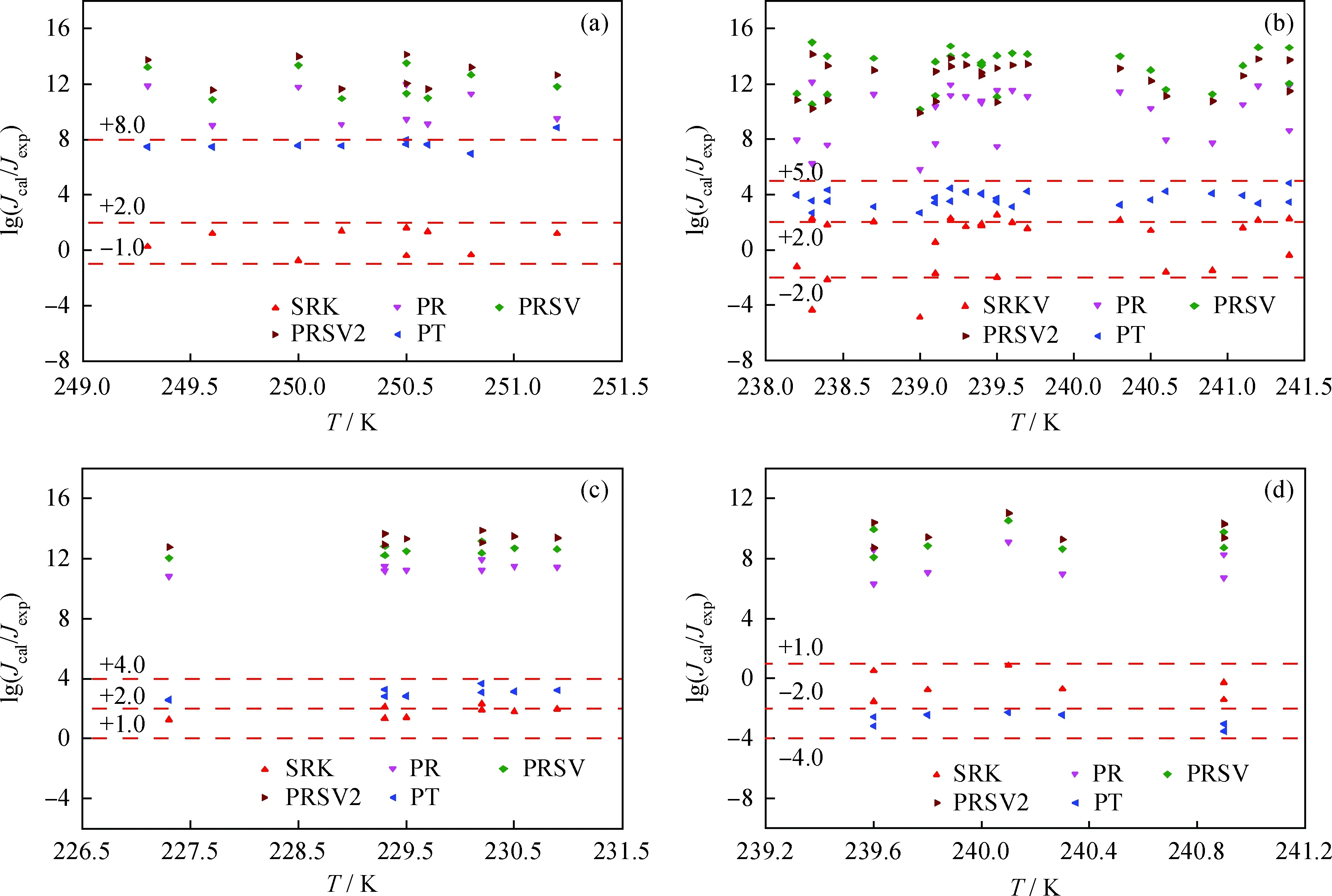
圖2 雙組分體系成核率修正模型2計算結果與實驗結果對比分析Fig.2 Comparison of calculated results by modified model 2 and experimental results of nucleation rate in binary vapor system(a) Methane and nonane, 250 K； (b) Methane and nonane, 240 K； (c) Methane and nonane, 230 K； (d) Methane and octane, 240 K

4 結 論

(1)針對雙組分氣體自發凝結經典成核模型中化學勢差計算方法復雜的缺點，引入逸度進行化學勢差的計算，既將真實氣體效應引入模型，簡化了計算過程；為保證雙組分成核計算模型的一致性，采用逸度代替分壓進行碰撞率的計算，改進了原經典成核模型中采用理性氣體假設這一缺點；同時，利用應用較廣泛的Benson & Shuttleworth液滴表面張力模型，將液滴半徑對表面張力的影響引入至單、雙組分成核計算模型中，形成了修正模型1。液滴表面張力模型的引入造成了修正模型1計算結果與實驗數據偏差較大。

(2)形成了僅考慮真實氣體效應修正、碰撞率計算修正的修正模型2。修正模型2較修正模型1計算結果更為接近實驗值。建議通過大量低溫實驗研究液滴表面張力，以求獲得準確的液滴表面張力模型。

(3)采用不同狀態方程進行化學勢差的計算中，采用SRK方程計算的修正模型2的預測效果最好，不同介質雙組分成核率預測偏差均在2個數量級以內，較Looijmans模型預測效果更好，大部分情況下較Kalikmanov的半現象學理論模型預測效果更好。因此，推薦采用修正模型2進行雙組分成核率的計算。

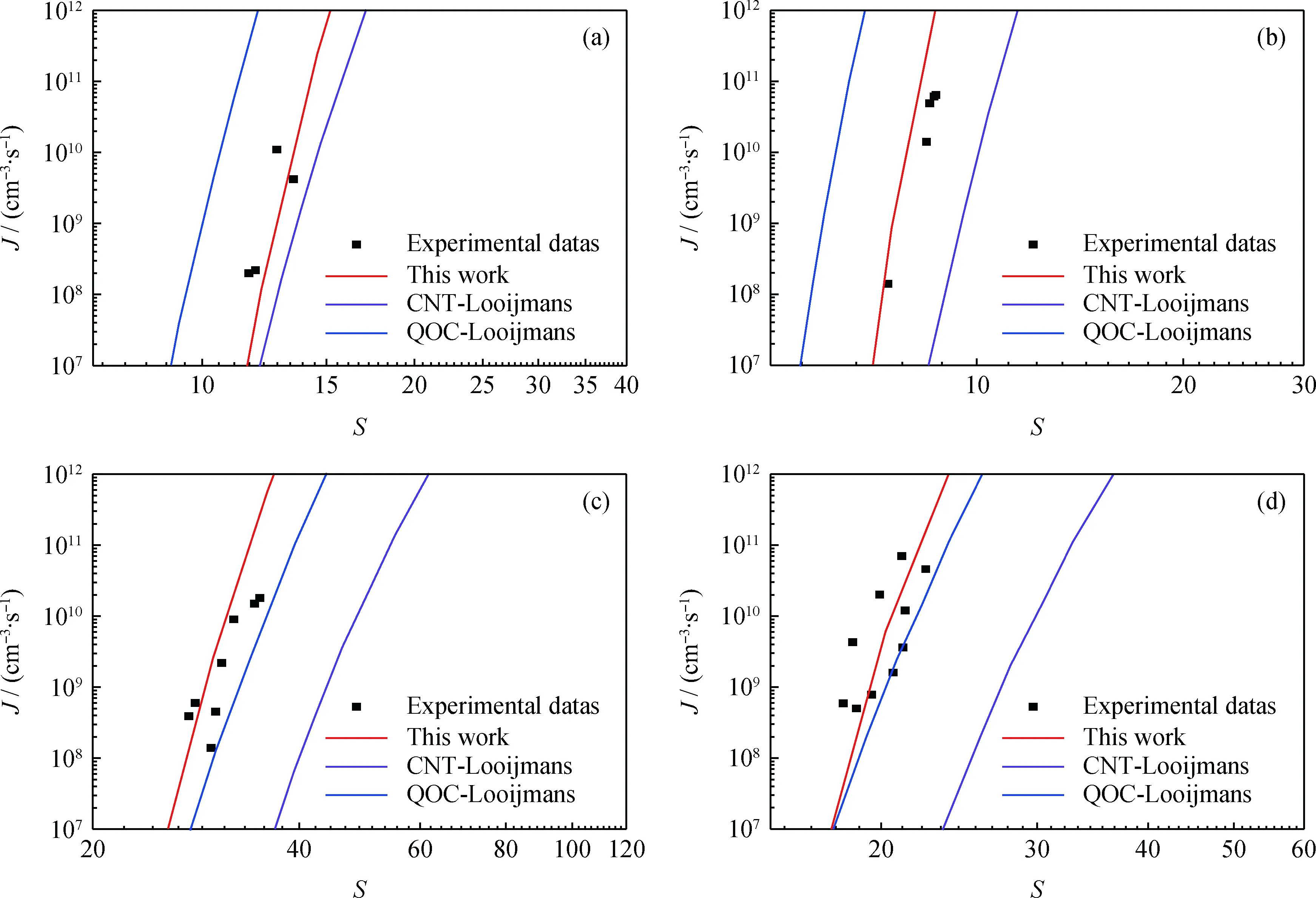
圖3 甲烷+壬烷體系不同成核率模型計算結果對比分析Fig.3 Comparison of calculated results of methane+nonane system by different nucleation models(a) 250 K-3 MPa； (b) 250 K-4 MPa； (c) 240 K-1 MPa； (d) 240 K-2 MPa； (e) 240 K-3 MPa； (f) 230 K-1 MPa

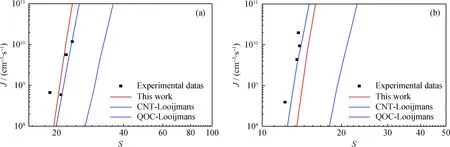
圖4 甲烷+辛烷體系不同成核率模型計算結果對比分析Fig.4 Comparison of calculated results of methane+octane system by different nucleation models(a) 240 K-1 MPa； (b) 240 K-2 MPa

符號說明：

A——液滴表面積，m2；

c1,c2——組分1和組分2的摩爾體積修正項，m3/mol；

D——自由能二階偏導數張量，J2/mol2;

fvi,fli——氣相、液相逸度，Pa;

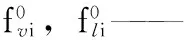
JBCNT——成核率，m-3/s;

K——成核動力前因子，m-3/s;

kB——波爾茲曼常數，1.3806×10-23J·K；

mi——組分i分子質量，g；

nli,nsi,nti——分別為液相、液滴表面分子數及液相和液滴表面分子數之和；

N——氣體混合物中分子數目，1/m3；

NA——阿伏伽德羅常數，6.02×1023/mol；

Nl——單個液滴中的分子數；

[Plm]——液相等張比容；

[Pvm]——氣相等張比容；

p——壓力，Pa；

pv、pl——氣相、液相分壓，Pa；

R——二維生長速率張量，s-2；

Rav——平均生長速率，s-1；

R11,R12,R21,R22——生長速率張量元素，s-1；

S——過飽和度；

T——溫度，K；

Vl——液滴體積，m3；

Vli——組分i偏分子體積，m3；

v——液相摩爾體積，m3/mol；

x1,x2——組分1和組分2的摩爾分數；

Z——Zeldovich因子；

ΔG——自由能障，J；

Δμi——化學勢差，J/mol；

φ——角度，弧度；

σ——液滴表面張力，N/m；

σ0——平面表面張力，N/m；

σm0——混合組分平面表面張力，N/m；

μli,μvi,μsi——液相、氣相、液滴表面化學勢，J/mol；

ρlm、ρvm——分別為液相和氣相密度，mol/m3；

上標

*——表示臨界成核狀態；

0——表示化學勢計算標準態。

[1] WEN C, CAO X W, YANG Y, et al. Swirling effects on the performance of supersonic separators for natural gas separation[J].Chemical Engineering & Technology, 2011, 34(9): 1575-1580.

[2] WEN C, CAO X W, YANG Y, et al. Supersonic swirling characteristics of natural gas in convergent-divergent nozzles[J].Petroleum Science, 2011, 8(1): 114-119.

[3] 曹學文. 超聲速旋流天然氣分離研究[D].西安: 西安交通大學, 2006.

[4] 文闖. 濕天然氣超聲速旋流分離機理研究[D].青島: 中國石油大學(華東), 2014.

[5] WEN C, CAO X W, YANG Y. Swirling flow of natural gas in supersonic separators[J].Chemical Engineering and Processing, 2011, 50(7): 644-649.

[6] WEN C, CAO X W, YANG Y, et al. Numerical simulation of natural gas flows in diffusers for supersonic separators[J].Energy, 2012, 37(1): 195-200.

[7] CAO X W, YANG W. Numerical simulation of binary-gas condensation characteristics in supersonic nozzles[J].Journal of Natural Gas Science and Engineering, 2015, 25:197-206.

[8] CAO X W, YANG W. The dehydration performance evaluation of a new supersonic swirling separator[J]. Journal of Natural Gas Science and Engineering, 2015, 27: 1667-1676.

[9] 邱中華. 含濕氣體在兩相渦流管中自發冷凝與分離性能研究[D].大連: 大連理工大學, 2008.

[10] 馬慶芬. 旋轉超音速凝結流動及其應用技術研究[D].大連: 大連理工大學, 2009.

[11] MA Q F, HU D P, HE G H, et al. Performance of inner-core supersonic gas separation device with droplet enlargement method[J].Chinese Journal of Chemical Engineering, 2009, 17(6): 925-933.

[12] 馬慶芬, 胡大鵬, 邱中華, 等. 超音速噴嘴渦流管氣體分離性能的數值模擬與實驗[J].石油學報(石油加工), 2011, 27(2): 297-307. (MA Qingfen, HU Dapeng, QIU Zhonghua, et al. Simulation and experiment on gas separation performance of a vortex tube with supersonic inlet nozzles[J].Acta Petrolei Sinica(Petroleum Processing Section), 2011, 27(2): 297-307.)

[13] 劉恒偉. 超音速分離管的研發及其流動與傳熱傳質特性的研究[D].北京: 北京工業大學, 2006.

[14] 蔣文明. 多組分凝結性超音速流傳熱傳質理論及實驗研究[D].北京: 北京工業大學, 2010.

[15] LIU H W, LIU Z L, FENG Y X, et al. Characteristic of a supersonic swirling dehydration system of natural gas[J].Chinese Journal of Chemical Engineering, 2005, 13(1): 9-12.

[16] 蔣文明, 劉中良, 劉恒偉, 等. 新型天然氣超音速脫水凈化裝置現場試驗[J].天然氣工業, 2008, 28(2): 136-138. (JIANG Wenming, LIU Zhongliang, LIU Hengwei, et al. Field test study on new type supersonic dehydrating facilities in natural gas purification plant[J].Natural Gas Industry, 2008, 28(2): 136-138.)

[17] 楊文, 曹學文. Laval噴管設計及在天然氣液化中的應用研究[J].西安石油大學學報(自然科學版), 2015, 30(2): 75-79. (YANG Wen, CAO Xuewen. Design of Laval nozzle and its application in liquefaction of natural gas[J].Journal of Xi’an Shiyou University(Natural Science Edition), 2015, 30(2): 75-79.)

[18] 楊文, 曹學文, 趙聯祁, 等. 超聲速旋流分離器內天然氣液化過程研究[J].石油機械, 2015, 43(5): 87-91. (YANG Wen, CAO Xuewen, ZHAO Lianqi, et al. Study on natural gas liquefaction process within supersonic cyclone separator[J].China Petroleum Machinery, 2015, 43(5): 87-91.)

[19] FLOOD H. Tr?pfchenbildung in übers?ttigtenthylalkohol-wasserdampf-gemischen[J].Z Phys Chem A, 1934, 170: 286-295.

[20] VOLMER M. Kinetic der Phasenbildung[M].Dresden and Leipzig, Steinkopff, 1939.

[21] REISS H. The kinetics of phase transitions in binary systems[J].J Chem Phys, 1950, 18(6): 840-848.

[22] LOOIJMANS K N H. Homogeneous nucleation and droplet growth in the coexistence region of n-alkane/methane mixtures at high pressures[D].Technische Universiteit Eindhoven, 1995.

[23] LOOIJMANS K N H, LUIJTEN C C M, HOFMANS G C J. Classical binary nucleation theory applied to the real mixturen-nonane/methane at high pressures[J].The Journal of Chemical Physics, 1995, 102(11): 4531-4537.

[24] WILEMSKI G. Composition of the critical nucleus in multicomponent vapor nucleation[J].The Journal of Chemical Physics, 1984, 80(3): 1370-1372.

[25] WILEMSKI G. Revised classical binary nucleation theory for aqueous alcohol and acetone vapors[J].Journal of Physical Chemistry, 1987, 91(10): 2492-2498.

[26] POLING B E, JOHN M P, JOHN P C. The Properties of Gases and Liquids[M].The McGraw-Hill Companies, 2004.

[27] TOLMAN R C. Consideration of the Gibbs theory of surface tension[J].The Journal of Chemical Physics, 1948, 16(8): 758-774.

[28] TOLMAN R C. The effect of droplet size on surface tension[J].The Journal of Chemical Physics, 1949, 17(3): 333-337.

[29] BENSON G C, SHUTTLEWORTH R. The surface energy of small nuclei[J].The Journal of Chemical Physics, 1951, 19(1): 130-131.

[30] 黃躍. 蒸汽透平中自發凝結及流動特性的理論和試驗研究[D].西安: 西安交通大學, 1987.

[31] CAMPBELL B A, BAKHTAR F. Condensation phenomena in high speed flow of steam[J]. Proc IME， 1971, 185(1): 395-405.

[32] CAMPBELL B A, BAKHTAR F. Condensation phenomena in high speed flow of steam—Experimental apparatus[J].Proc IME, 1973, 187(1): 199-205.

Modification of Models for Binary Component Vapor Spontaneous Nucleation

YANG Wen1， HOU Zhiqiang2, CHEN Peng3, CAO Xuewen4

(1.SINOPECSalesCo.,Ltd.,PipelineTechnologyCenter,SouthChinaBranch,Guangzhou510620,China;2.SINOPECGroupCompany,EngineeingDepartment,Beijing100728,China;3.ZhengzhouManagementOffice,PetroChinaWestEastGasPipelineCompany(PetroChinaWestEastGasMarketingCompany),Zhengzhou450000,China; 4.CollegeofPipelineandCivilEngineering,ChinaUniversityofPetroleum,Qingdao266580，China)

In view of the disadvantages of the binary classical nucleation theory (BCNT)model without considering real gas effects or Looijmans modified classical nucleation model with complex chemical potential difference computation, grow rate in nucleation kinetic item without considering real gas effects and surface tension computation with considering the droplet diameter effect, new modified models were proposed. The minimum deviation between the calculated results by modified model 1 with all disadvantages of BCNT and Looijmans being modified and experimental results was in the order of 2, due to the introduction of inaccurate droplet surface tension model. The minimum deviation between the calculated results by modified model 2 without droplet surface tension modification and experimental results was less than the order of 2. The comparison of modified model 2 to Looijmans model and Kalikmanov model for different binary component system showed that the modified model 2 was a good choice for the prediction of condensation nucleation rate in binary component system.

binary component； condensation； equation of state； vapor liquid equilibria； experimental validation

2016-06-17

國家自然科學基金項目(51274232)、國家自然科學基金青年基金項目(51406240)和山東省自然科學基金青年基金項目(ZR2014EEQ003)資助

楊文，男，博士，從事多相流及油氣田集輸技術方面的研究；E-mail:yangwen112006@163.com

1001-8719(2017)02-0273-08

TE86

A

10.3969/j.issn.1001-8719.2017.02.012