手寫體數字字符識別算法仿真比較研究

陳 龍， 郄小美， 黃信靜， 林 虎

(杭州電子科技大學 電子信息學院， 杭州 310018)

手寫體數字字符識別算法仿真比較研究

陳 龍， 郄小美， 黃信靜， 林 虎

(杭州電子科技大學 電子信息學院， 杭州 310018)

采用BP神經網絡、原始極限學習機、正則極限學習機和傅里葉變換優化極限學習機算法分別進行手寫體數字字符識別仿真實驗，通過MINIST數據庫中的10 000個手寫體數字樣本訓練神經網絡數據傳輸過程中的參數，用訓練所得神經網絡參數進行手寫體數字識別仿真測試。比較4種算法的仿真效果，BP網絡識別效果最好、訓練速度最慢，原始極限學習機訓練速度最快，正則極限學習機和傅里葉變換極限學習機優化算法識別正確率高于原始極限學習機，但增加了算法的時間復雜度。將該手寫體數字字符識別仿真實驗用于學生實驗教學，可加強學生對神經網絡相關知識的學習和理解，提高學生編程和工程應用能力。

神經網絡； 極限學習機； 手寫數字識別； 實驗教學

0 引 言

神經網絡是模仿人的大腦神經網絡結構和功能而建立的一種信息處理系統，具有高度的非線性特征。神經網絡在神經科學、人工智能和計算機科學等領域具有廣泛應用，其中Back Propagation (BP)神經網絡是目前應用最廣泛的神經網絡模型之一[1-3]。BP神經網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，包括信號的正向傳播和誤差的反向傳播兩個過程。在多次信號的正向傳播和誤差的反向傳播過程中，神經網絡各權值通過梯度下降法得到修正，使得網絡輸出誤差滿足要求，或達到設定的學習次數為止[4]。極限學習機是一種快速的單隱層前饋神經網絡(Single-hidden Layer Feedforward Neural Network, SLFN)，在2004年由黃廣斌教授等人提出，該算法通過大量的樣本計算確定神經網絡的傳輸參數，相對于BP神經網絡因使用梯度下降法迭代計算傳輸參數耗費大量時間，極限學習機計算過程無需迭代，具有訓練速度快的特點[5-7]。

手寫數字識別在郵件分類、車牌識別和銀行票據識別等方面的廣泛應用使之成為了圖像處理和模式識別領域的一個研究熱點。目前已經存在的手寫字符識別方法包括模板匹配法、支持向量機和決策樹等[8-12]。本文采用BP神經網絡、原始極限學習機、正則極限學習機和傅里葉變換優化極限學習機算法進行手寫體數字字符識別仿真實驗，對4種算法的識別率和時間復雜度進行了比較研究。該手寫體數字字符識別實驗用于本科生實驗教學可提高學生對神經網絡的理解和認識，讓學生掌握利用神經網絡實現手寫體數字字符識別的方法，提高同學們綜合運用所學知識解決實際問題的能力[13]。

1 極限學習機

單隱含層前饋神經網絡模型如圖1所示，包括輸入層、隱含層和輸出層，其中隱含層第i個神經元的模型如圖2所示，隱含層第i個神經元的輸入xj與對應的權值wij相乘求和后加偏置b，經激活函數g(x)限幅得隱含層神經元輸出為

(1)

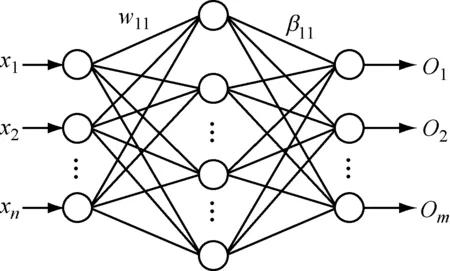
圖1 單隱含層前饋神經網絡模型圖

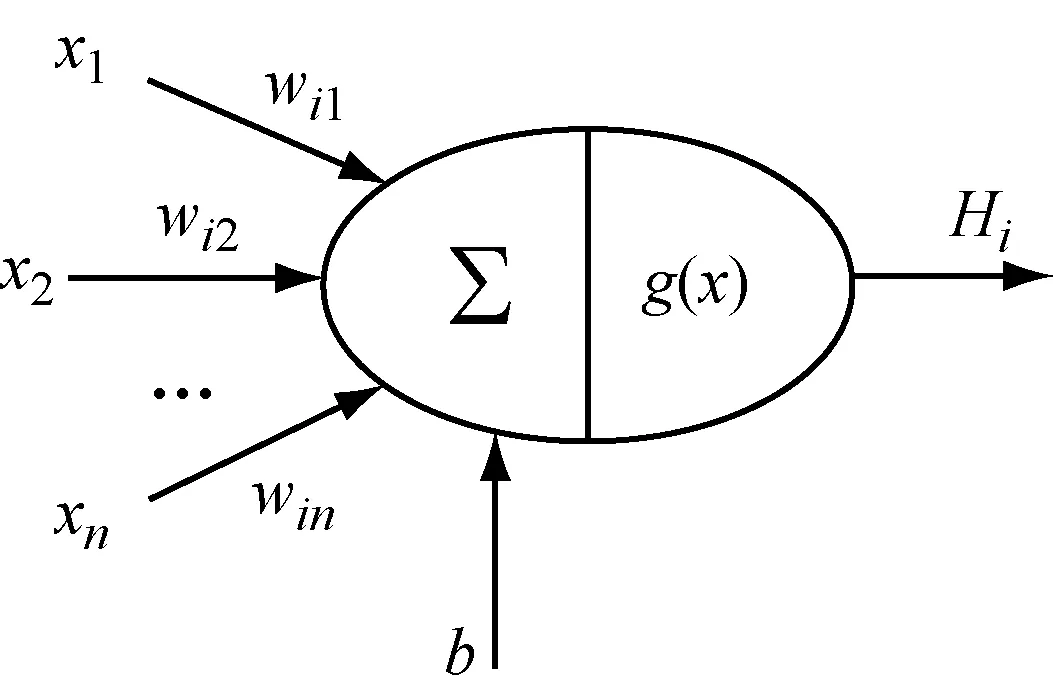
圖2 隱含層第i個神經元模型圖

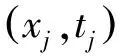
(2)

為了使模型的實際輸出oj零誤差逼近于期望輸出tj，即

(3)

輸入權值矩陣W和偏置矩陣b可隨機設定[5-6]，根據Moore-Penrose廣義逆矩陣和最小范數最小二乘解[14]的相關定理，采用矩陣表達式得:

(4)

式中：H+為隱含層輸出矩陣H的Moore-Penrose廣義逆矩陣。

神經網絡訓練過程即求傳輸參數的過程，對ELM而言即求輸出矩陣β的過程，根據式(1)～(4)完成ELM的參數訓練過程，用所得輸出權值矩陣β進行測試，對測試結果進行對比和分析，測試結果若不滿足要求，可通過適當增加訓練樣本或增加隱含層神經元個數改善測試結果。

2 極限學習機優化算法

2.1 正則極限學習機

正則極限學習機是一種通過參數γ來調節原始極限學習機數學模型存在的經驗和結構風險的比例，從而提高原始極限學習機泛化能力，防止原始極限學習機易導致過擬合問題的優化算法[15]，其數學模型由下式表示，使J值達到最小：

(5)

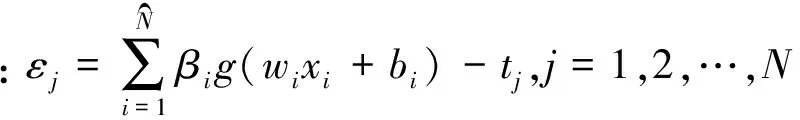
用拉格朗日乘子法求解式(5)所示數學模型的最優解，R-ELM的數學模型可用拉格朗日方程表示為：

L(β,ε,α)=

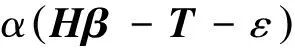
(6)

求得輸出權值矩陣

(7)

正則極限學習機通過優化參數γ和矩陣D優化輸出權值矩陣，通過式(7)計算所得輸出權值矩陣β進行正則極限學習機的測試。

2.2 傅里葉變換優化極限學習機算法

傅里葉變換是一種信號分析的方法，傅里葉變換優化極限學習機算法[16]將隱含層神經元的輸出做傅里葉變換，將圖像的特征轉換為特定的頻率信號，通過拉格朗日乘子法優化原始極限學習機的輸入權值矩陣，具體模型如下式所示，使J取最小值：

(8)

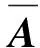
(9)

用拉格朗日乘子法求解，列寫拉格朗日方程為：

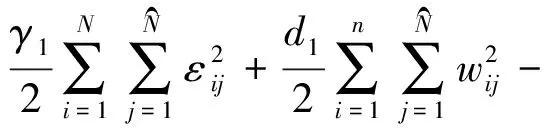
(10)

對式(10)求梯度得：

(11)

求得優化后的輸入權值矩陣為：

(12)

優化輸出權值矩陣的數學模型為

(13)

式中，ε=O-T=Hβ-T。列寫優化輸出矩陣的拉格朗日方程為：

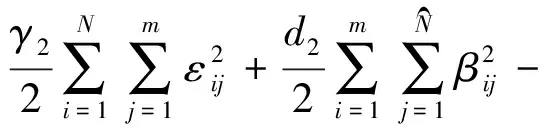
(14)

與以上優化輸入權值矩陣求解方式相同，解得優化后的輸出權值矩陣為

(15)

傅里葉變換優化極限學習機算法在對輸出權值矩陣β進行優化之前對輸入權值矩陣w也進行了優化。

3 手寫體數字字符識別仿真實驗

實驗采用BP、ELM、R-ELM和DFT-ELM 4種算法進行手寫體數字字符識別仿真實驗，樣本選擇MINIST數據庫中的10 000個手寫體數字作為訓練樣本，部分樣本圖片如圖3所示，各字符筆畫的粗細和形狀各不相同，具有代表性。神經網絡經過訓練后，選擇1 000個樣本進行測試，其中0～9各數字均為100個，最后對4種算法手寫體數字字符識別結果進行對比和分析。

圖3 部分樣本圖片

3.1 手寫體數字字符樣本預處理

MINIST樣本庫中手寫體數字圖像均為28×28的灰度圖，黑色值為0，白色值為255。為減少運算量，降低數據維數，采用式(16)對樣本圖片進行降維，其中r=c=2，圖4為數字樣本圖片5的降維結果，經過降維后圖像像素為14×14。圖5為降維后的樣本圖片5的數據特征，橫坐標為像素點順序，縱坐標為灰度值。

(16)

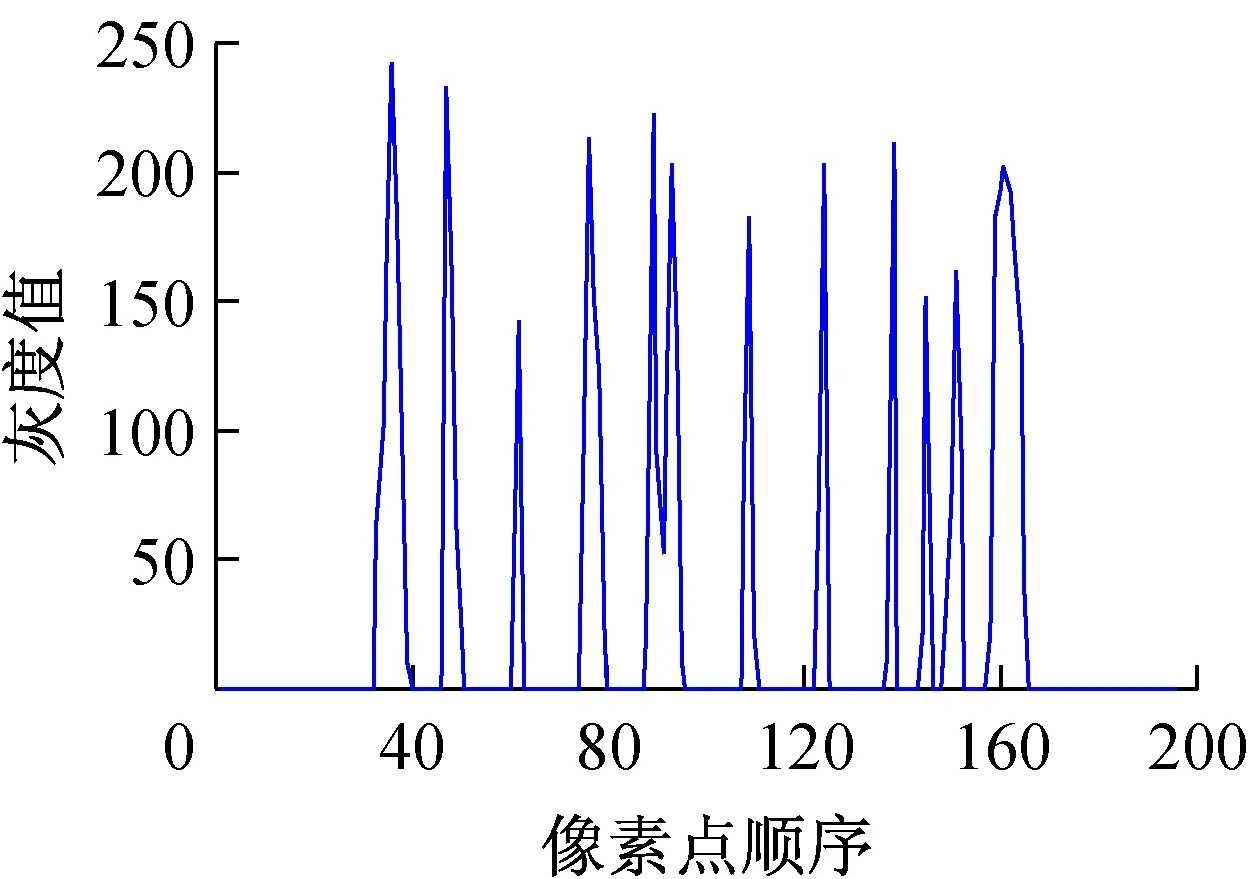
圖5 樣本圖片5的灰度特征圖

3.2 手寫體數字字符識別仿真

(1) 基于BP神經網絡的手寫體數字字符識別算法仿真。Matlab工具箱中為神經網絡的訓練提供了大量的庫函數，本實驗中采用newff函數創建BP神經網絡，train函數完成BP神經網絡的訓練，圖6所示為隱含層神經元個數為200時BP神經網絡的訓練過程。圖6顯示了該BP神經網絡輸入層具有196個神經元，隱含層具有200個神經元，輸出層具有10個神經元，最大迭代次數為1 000次，訓練時間為24 s。

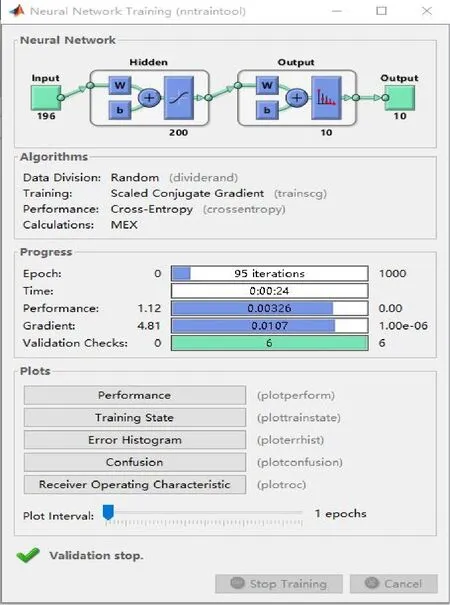
圖6 BP神經網絡訓練過程

(2) 基于ELM算法的手寫體數字字符識別算法仿真。經過數據初始化后，通過對訓練樣本的學習確定ELM傳輸過程中的傳輸參數，即輸出權值矩陣β，期望輸出T為一個1×10的矩陣，數字為0～9時對應的期望輸出，如表1所示。

表1 各數字對應的期望輸出T

當隱含層神經元個數為200時測試所得神經網絡的輸出如圖7所示，圖7(a)～(j)分別表示測試樣本為0～9時ELM網絡輸出。

(3) R-ELM算法實現手寫體數字字符識別。R-ELM優化算法的目標是提高原始極限學習機的泛化能力，根據式(7)計算R-ELM算法的輸出權值矩陣，其中調節參數γ=0.25，矩陣D取單位對角矩陣，輸出方式與ELM相同。

(4) DFT-ELM算法實現手寫體數字字符識別。DFT-ELM根據式(12)計算輸入權值矩陣，式(15)計算輸出權值矩陣，其中d1=d2=0.01，γ1=γ2=0.5，輸出方式與ELM相同。

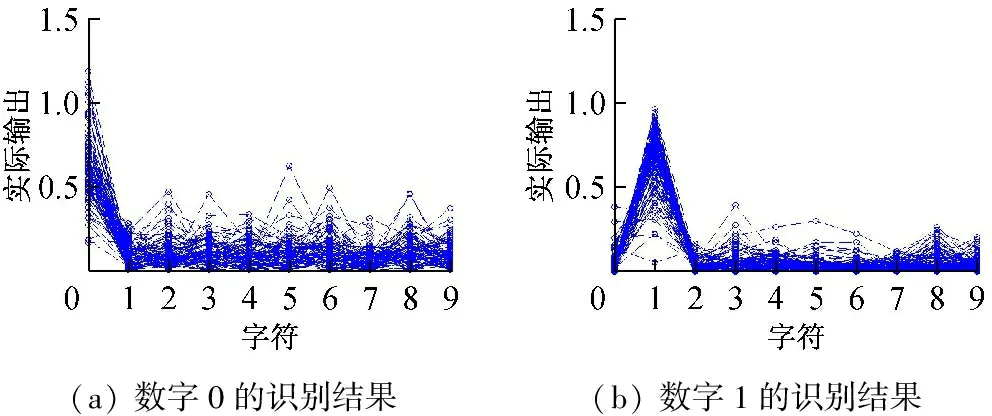
(a)數字0的識別結果(b)數字1的識別結果

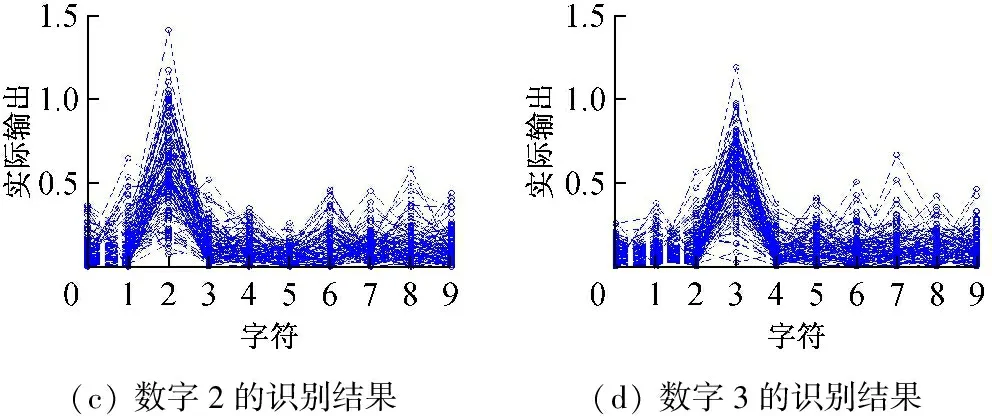
(c)數字2的識別結果(d)數字3的識別結果

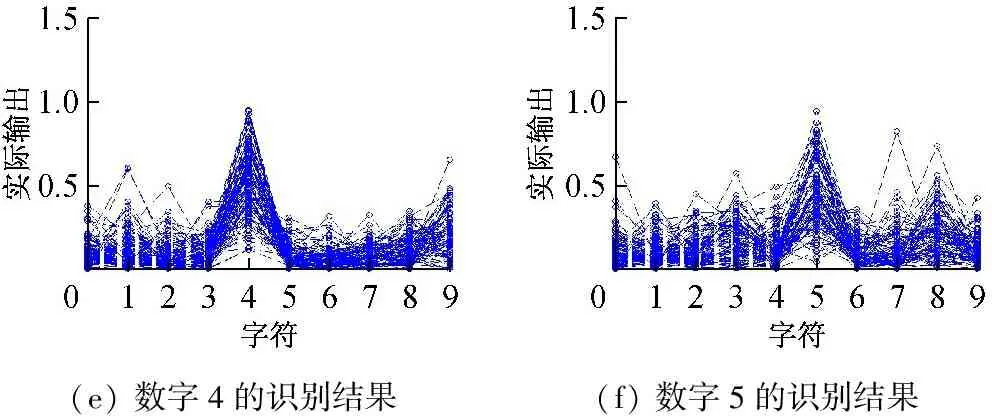
(e)數字4的識別結果(f)數字5的識別結果

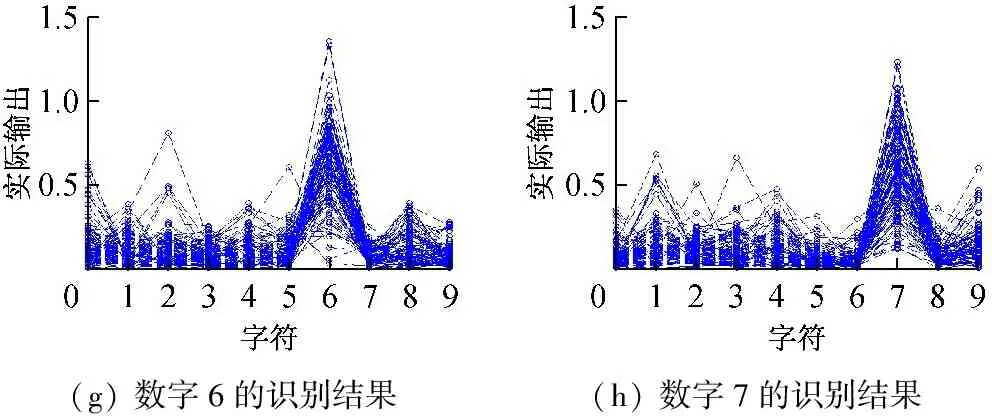
(g)數字6的識別結果(h)數字7的識別結果

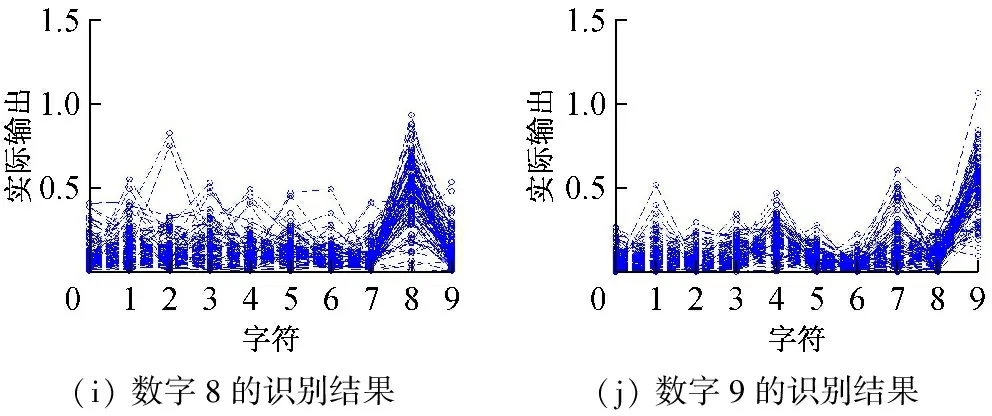
(i)數字8的識別結果(j)數字9的識別結果

圖7 神經元個數為200時ELM算法識別結果

3.3 實驗結果分析與對比

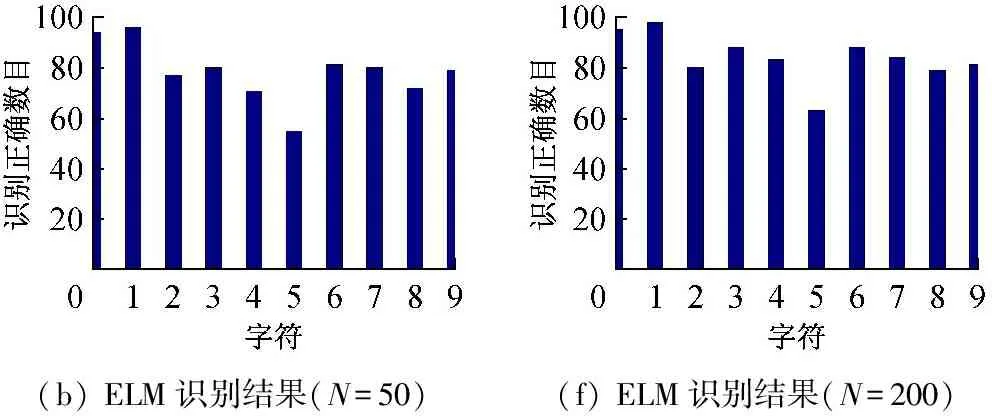
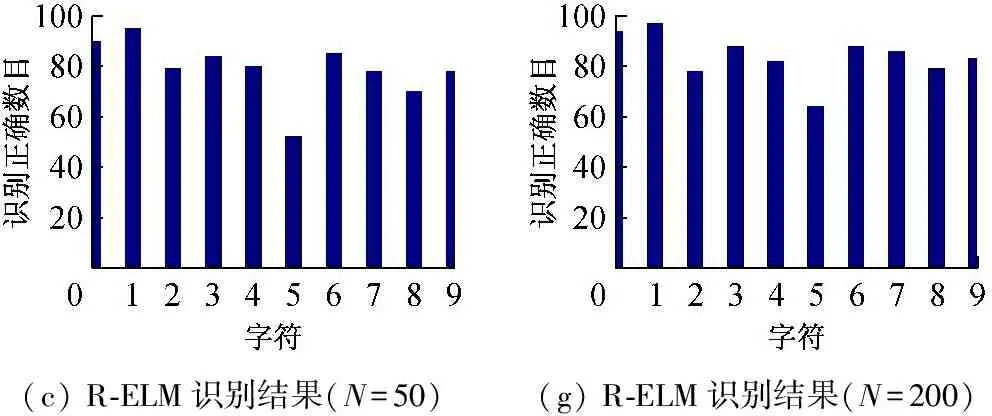
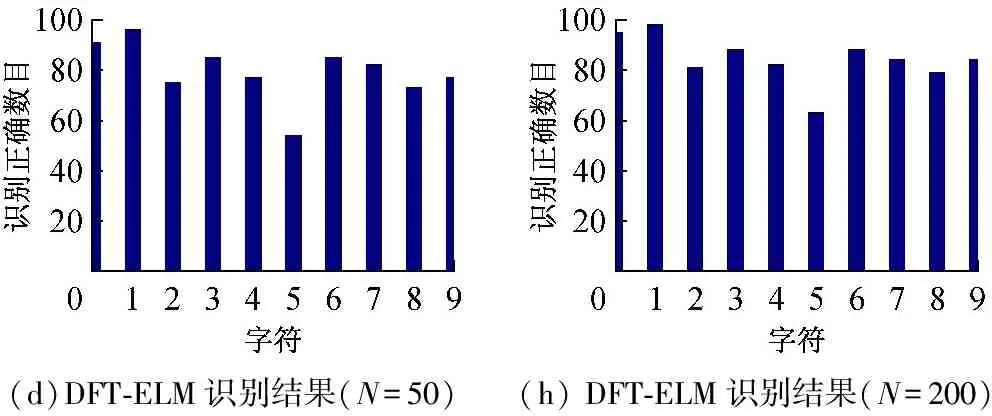
為了比較BP、ELM、R-ELM和DFT-ELM 4種算法對手寫體數字字符的識別效果，統計各數字識別正確的個數，識別結果如圖8所示，橫坐標為待識別的數字，縱坐標為該數字識別正確的個數，其中圖8(a)、(b)、(c)、(d)為隱含層神經元個數為50時各算法的識別結果，圖8(e)、(f)、(g)、(h)為隱含層神經元個數為200時各算法的識別結果。

對圖8所示識別結果進行統計，4種算法在隱含層神經元個數分別為50和200時各數字字符識別正確的個數及平均識別率如表2各數字字符識別結果統計所示，各算法實現過程所需時間如表3所示。由表2各數字識別結果統計和表3各算法識別過程所需時

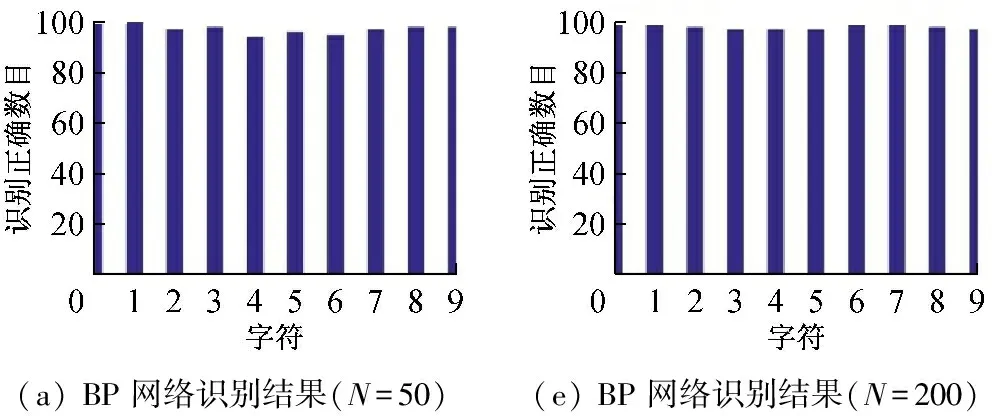
(a)BP網絡識別結果(N=50)(e)BP網絡識別結果(N=200)

(b)ELM識別結果(N=50)(f)ELM識別結果(N=200)

(c)R?ELM識別結果(N=50)(g)R?ELM識別結果(N=200)

(d)DFT?ELM識別結果(N=50)(h)DFT?ELM識別結果(N=200)

圖8 隱層神經元個數為50和200時4種算法識別結果

間可知，各算法在隱含層神經元個數為200時的平均識別率均高于隱含層神經元個數為50時的平均識別率，且BP網絡的識別率遠遠高于ELM及ELM的優化算法，但BP網絡的訓練過程消耗大量時間。

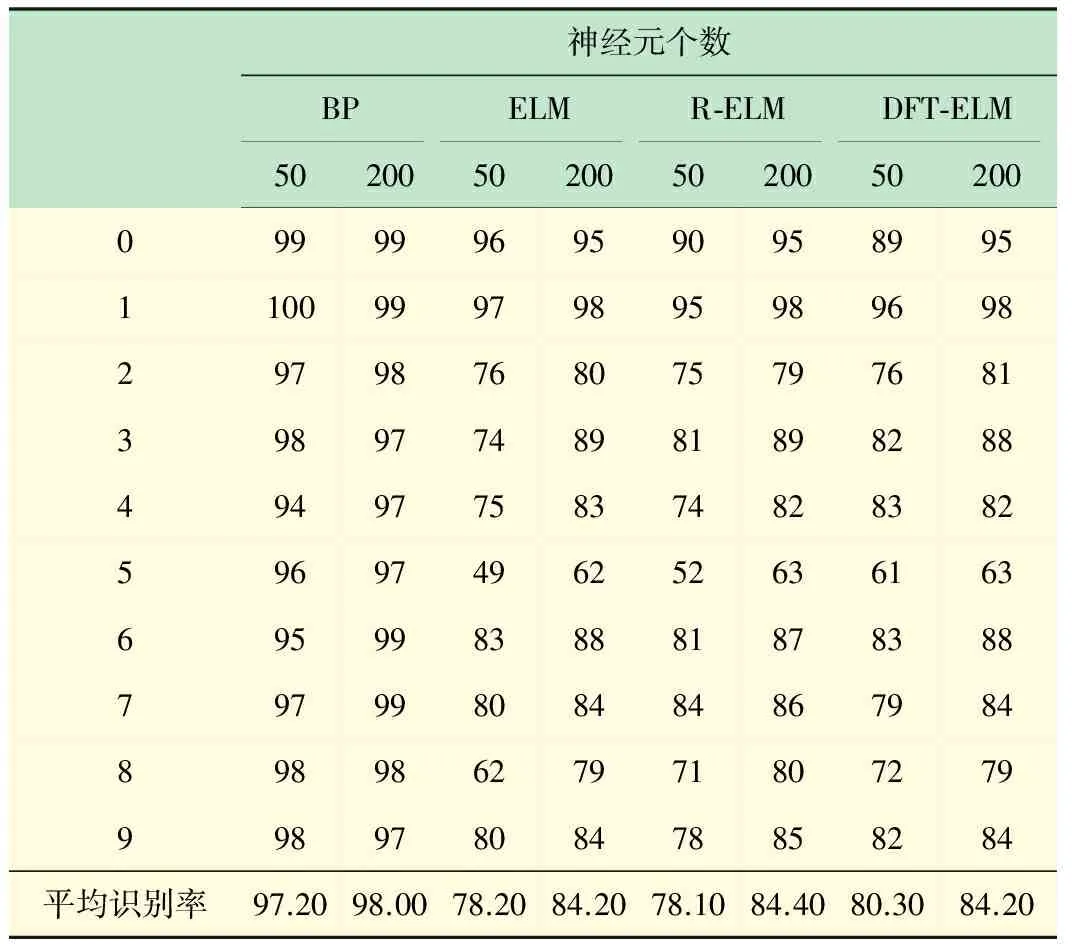
表2 各數字識別結果統計

表3 各算法識別過程所需時間

4 結 語

該實驗以手寫體數字字符識別為例，驗證了BP神經網絡、極限學習機及其優化算法的性能，極限學習機及其優化算法較傳統的BP神經網絡大大減少了算法的時間復雜度。BP神經網絡已經在各領域得到了廣泛應用，極限學習機及其優化算法除適用于手寫體數字字符的識別，也可用于其他字符和圖形符號的識別，同時為處理大批量數據時降低訓練集規模、減少運算量和提高效率提供了新思路。將該手寫體數字字符識別實驗應用于本科生實驗教學，通過Matlab軟件編程實現手寫體數字字符識別過程，讓學生對神經網絡的實現過程更加明確，其中圖像降維和特征提取過程讓學生對模式識別有了一定了解，掌握了利用Matlab軟件進行程序編寫和神經網絡仿真實驗的技能。

[1] 曹旭帆,胡同森.基于BP神經網絡的含噪字符識別系統及Matlab實現[J].實驗室研究與探索,2008(1):76-80.

[2] 蔣鼎國. 基于改進型BP神經網絡PID控制器的溫室溫度控制技術[J].實驗室研究與探索,2015(1):9-13.

[3] 曹旭帆,葉 舟,萬 俊,等.基于BP神經網絡的函數逼近實驗及Matlab實現[J].實驗室研究與探索,2008(5):34-38.

[4] 周 品，Matlab神經網絡設計與應用[M].北京：清華大學出版社，2013，164-171.

[5] Huang Guangbin,Qin YuZhu, CheeK. Extreme learning machine:Theoryandapplications [J]. Neuroco-mputing，2006，70：489-501.

[6] Huang Guangbin,Wang Dianhui, Lan Yuan. Extreme learning machines: a survey [J]. Int.J. Mach. Learn. & Cyber.(2011)2:107-122.

[7] 趙文華,張文濤,杜欣慧. 形相似的ELM在電鐵短期負荷預測中應用[J]. 實驗室研究與探索,2013(11):279-282,328.

[8] 潘煒深,金連文,馮子勇. 基于多尺度梯度及深度神經網絡的漢字識別[J].北京航空航天大學學報,2015(4):751-756.

[9] 楊 怡,王江晴,朱宗曉. 基于仿射傳播聚類的自適應手寫字符識別[J]. 計算機應用,2015(3):807-810.

[10] 李 琢,王亞利,盧奇茂,等. 帶有格線邊框的手寫體數字串處理系統[J]. 清華大學學報(自然科學版),2002(3):387-390.

[11] 王 璇,薛 瑞.基于BP神經網絡的手寫數字識別的算法[J]. 自動化技術與應用,2014(5):5-10.

[12] 王一木,潘 赟,龍彥辰,等.基于自組織映射的手寫數字識別的并行實現[J]. 浙江大學學報(工學版),2014(4):742-747.

[13] 王艷芬,叢瀟雨,王 剛,等. 基于Simulink的Chirp-UWB通信系統綜合實驗設計[J]. 實驗室研究與探索,2015(7):90-93，234.

[14] 張娟娟. 穩健線性回歸中再生權最小二乘法的有效性研究[D].太原：太原理工大學,2013.

[15] Deng W, Zheng Q, Chen L. Regularized Extreme Learn- ing Machine[C].Computational Intelligence and Data Mining, 2009. CIDM '09.IEEE Symposium on IEEE, 2009:389-395.

[16] Man ZhiHong,LeeK,WangDianhui,etal. A robust single-hidden layer feedforward network based pattern classifier[J].IEEE Transactions on Neural Networks and Learning Systems，2011，P-3489-R2.

A Comparative Study on Handwritten Digital Character Recognition Algorithm by Simulation

CHENLong，QIEXiao-mei，HUANGXin-jing，LINHu

(School of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018,China)

In this paper, we use back propagation (BP) neural network, extreme learning machine (ELM), regularized extreme learning machine (R-ELM) and DFT extreme learning machine (DFT-ELM) to realize the recognition of handwritten digital characters. Ten thousands handwritten digital samples from MINIST database are used to train neural network parameters in the process of data transmission, use the trained neural network parameters to do handwritten digital recognition test. In the light of the simulation results, BP has the best recognition accuracy, regardless of the training speed. Compared with ELM, although R-ELM and DFT-ELM have higher recognition accuracy, both of them increase the time complexity. This handwritten digital recognition simulation experiment can use to strengthen student's studying and understanding of neural networks and improve students' ability in programming and engineering application.

neural networks; extreme learing machine(ELM); handwritten digital recognition; experiment teaching

2016-03-03

浙江省2013年高等教育課堂教學改革項目(kg2013125)；浙江省2015年度高等教育教學改革項目(jg2015060)

陳 龍(1979-)，男，山東寧陽人，碩士，副教授，研究方向為嵌入式系統設計與應用、神經網絡與機器學習。

Tel.：0571-86915094； E-mail:chenlong@hdu.edu.cn

G 642.423

A

1006-7167(2017)01-0093-05