對稱張量特征值問題的一種預處理迭代算法

顧傳青,李龍

(上海大學理學院,上海 200444)

?快報?

對稱張量特征值問題的一種預處理迭代算法

顧傳青,李龍

(上海大學理學院,上海 200444)

移位對稱高階冪法(shifted symmetric high order power method,SS-HOPM)是一種求解張量Z-特征值的著名迭代算法.用Newton法對該算法實施初值預條件處理,得到了對稱張量特征值問題的一種Newton預條件移位對稱高階冪法(preconditioning SS-HOPM, PSS-HOPM).用兩個數值例子驗證并得出,與SS-HOPM相比,該算法在幾乎不增加計算時間的條件下能計算出更多的特征值.

移位對稱高階冪法;Newton法;Newton預處理方法

最近,張量特征值問題由于與大數據及其應用直接相關[1],在國內外受到了廣泛的關注[2-3].張量特征值[4]的定義如下.

定義1假設A是一個m階n維的實對稱張量,則對任何n維向量x,定義

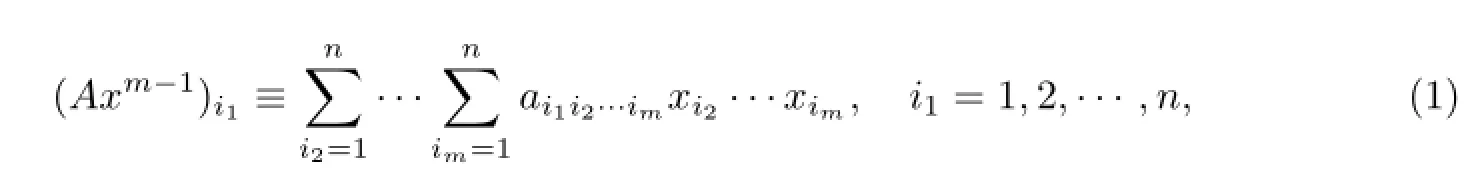
則λ∈R是張量A的一個特征值.如果存在x∈Rn,使得

則向量x是對應的特征向量,(λ,x)稱為一個特征對.

定義2定義1的張量Z-特征值問題是由齊利群[5-6]和Lim[7]提出的.特別地,Lim[7]指出任何特征對(λ,x)是一個非線性優化問題的Karush-Kuhn-Tucker(KKT)點,即一個約束的不動點.

1 Newton法和移位對稱高階冪法

1.1 Newton法[8]

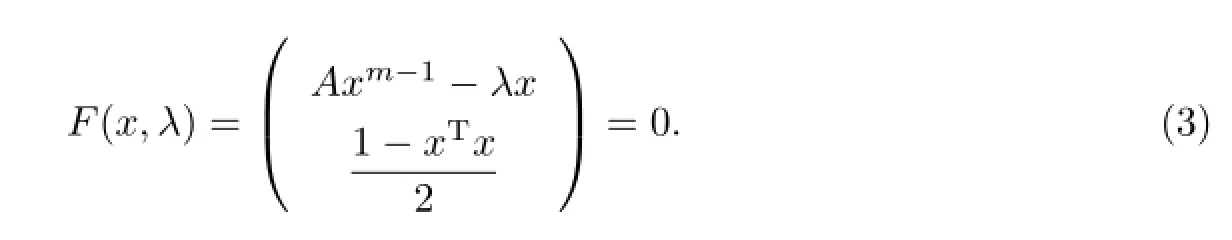
為了求解張量特征值問題(2),Newton法將其轉化為以下等價的非線性方程組:若(n+1)維向量(x?,λ?)為非線性方程組(3)的解,則(x?,λ?)為張量A的Z-特征對.

為了利用Newton法解問題(3),假設已知A為m階n維實對稱張量,則F(x,λ)的Jacobian矩陣F′(x,λ)是對稱矩陣,其計算公式(證明過程見文獻[9])為

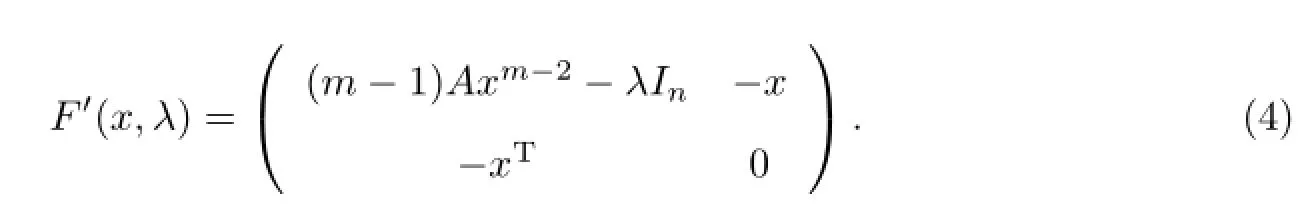
算法1Newton法

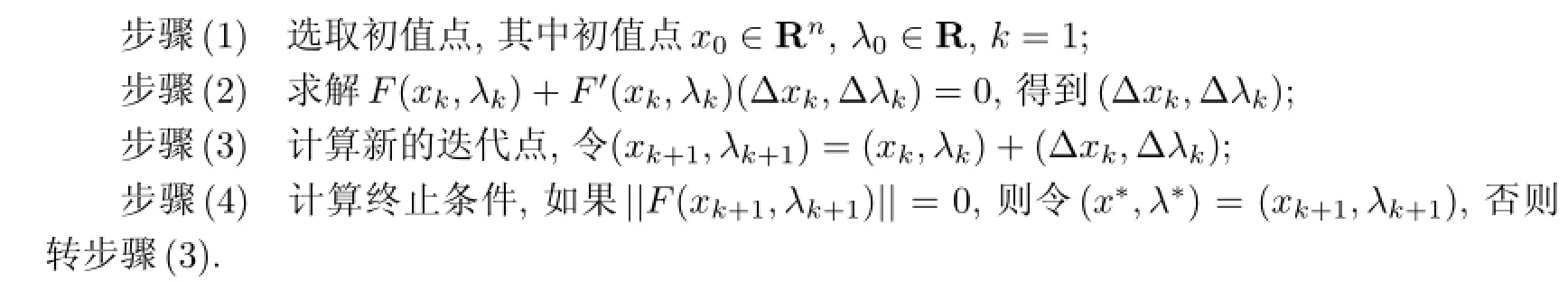
上述算法是局部收斂的,即只有初始點選在收斂域內才能保證收斂.

1.2 移位對稱高階冪法

Kolda等[10]提出了移位對稱高階冪法(shifted symmetric high order power method,SSHOPM),計算格式如下.

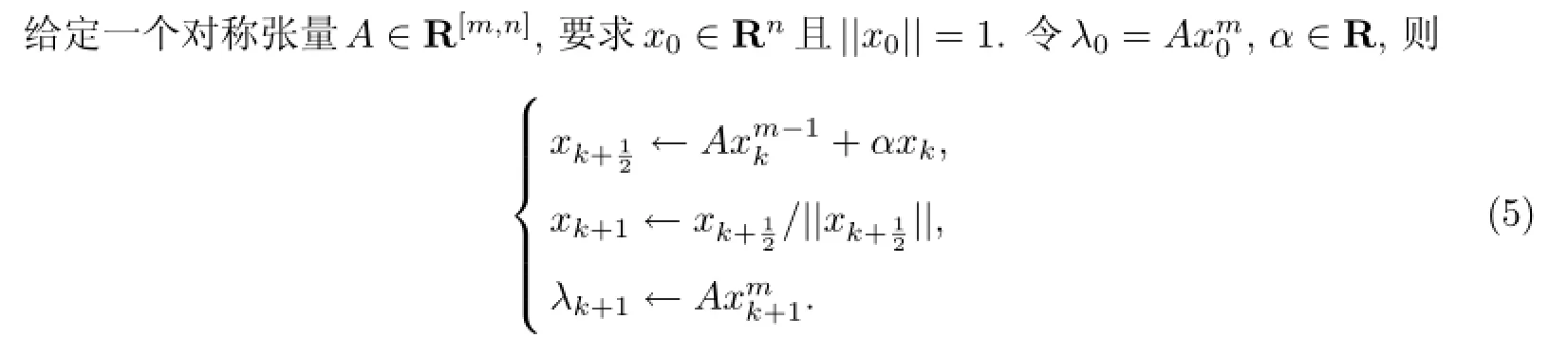
SS-HOPM是改進對稱高階冪法(S-HOPM)后得到的.S-HOPM僅在滿足某些特定條件下才會收斂,而SS-HOPM則在S-HOPM基礎上添加位移因子α,使得文獻[10]中式(4.1)成為凸多項式或者凹多項式,這樣便可保證乘冪法的收斂性.

2 對稱張量特征值問題的一種Newton預處理迭代算法

結合Newton法和移位對稱高階冪法,本工作提出求解張量特征值問題的一種Newton預處理迭代算法.本算法的基本思想是:首先任意給定一個初始向量,給定一個合適的精度,然后利用Newton法得到一個粗糙的解,最后將該粗糙解作為移位的對稱高階冪法的初始解向量,執行移位對稱高階冪法,直到達到收斂精度.本算法中,利用參數ε1控制Newton法向SS-HOPM轉換,ε2為SS-HOPM結束達到的精度.Newton預條件移位對稱高階冪法(preconditioning SS-HOPM,PSS-HOPM)的具體計算格式如式(5)所示,將計算格式xi+1=xi?F?1(xi)f(xi)迭代運算一定次數后得到的xk值作為式(5)的初值x0.

算法2預條件移位對稱高階冪法(PSS-HOPM)

由于本工作給出的PSS-HOPM是先由Newton法對初始向量實施優化,得到的向量再作為SS-HOPM的初始向量,故其收斂性可由下面SS-HOPM的收斂性定理保證.

定理1[10]設A∈R[m,n]是對稱張量,且對于α>β(A)(β(A)由文獻[10]中定義),算法2產生的迭代序列{λk,xk}滿足如下性質:①序列{λk}單調不減,且存在λ?,使得λk→λ?;②序列{xk}有一個聚點;③對于每一個聚點x?,每對{λ?,x?}都是張量A的一個特征對;④如果A的特征對為有限個,則存在x?,使得xk→x?.

3 數值實驗

本工作使用文獻[10]給出的兩個數值算例來說明預條件移位對稱高階冪法(PSSHOPM)的有效性.考慮A∈R[3,3]和A∈R[4,3]分別為奇數階和偶數階的情況,位移α分別取2和1,向量殘差的2-范數作為算法的停止準則,計算精度ε1=0.01,ε2=10?6.本工作在文獻[10]中的例1.1和例1.2所描述的實驗條件下用SS-HOPM和PSS-HOPM分別測試了100次,實驗結果如表1和2所示.

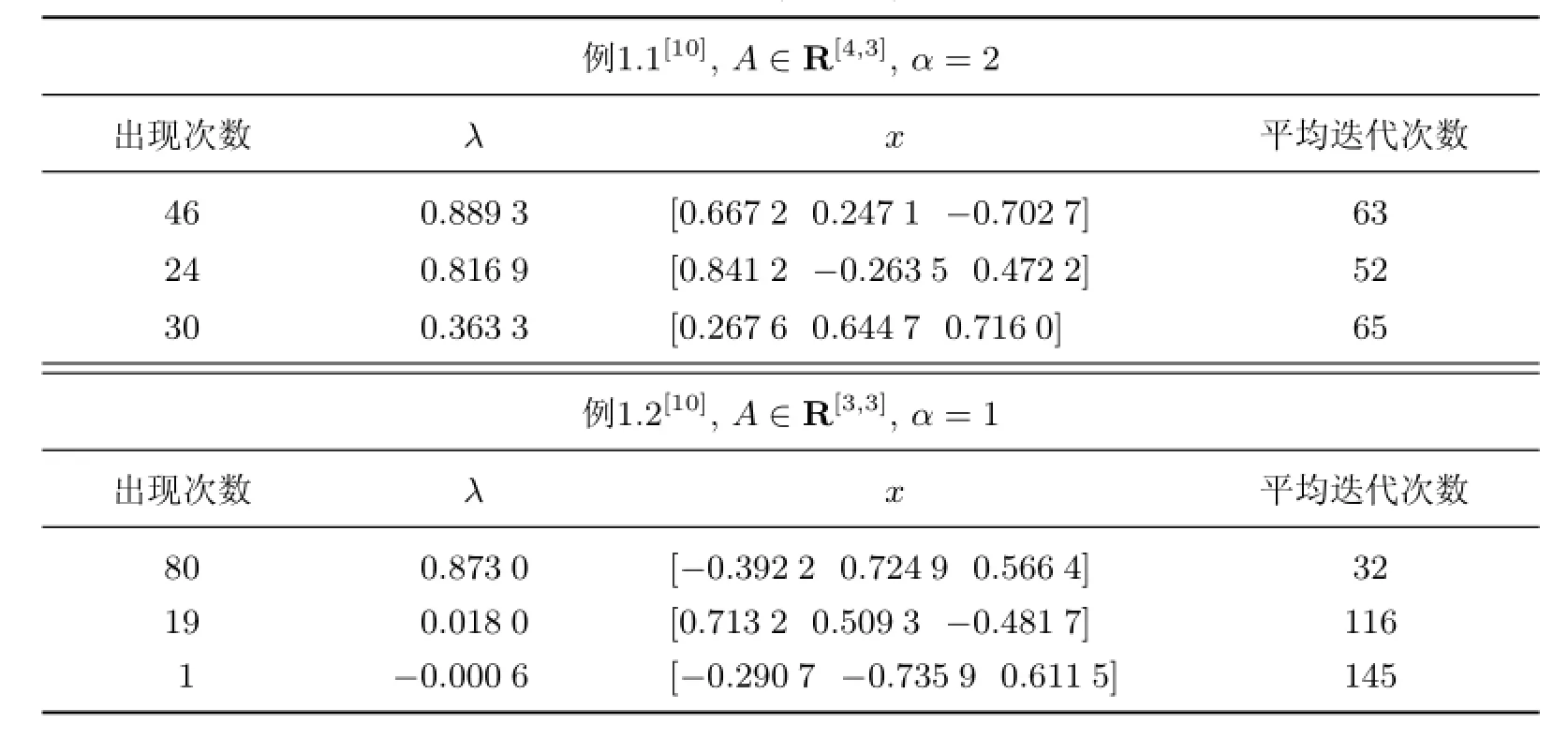
表1 由100個隨機初始點通過SS-HOPM(凸)計算得到的特征值Table 1 Eigenvalues obtained by SS-HOPM(convex)calculation of 100 random initial points

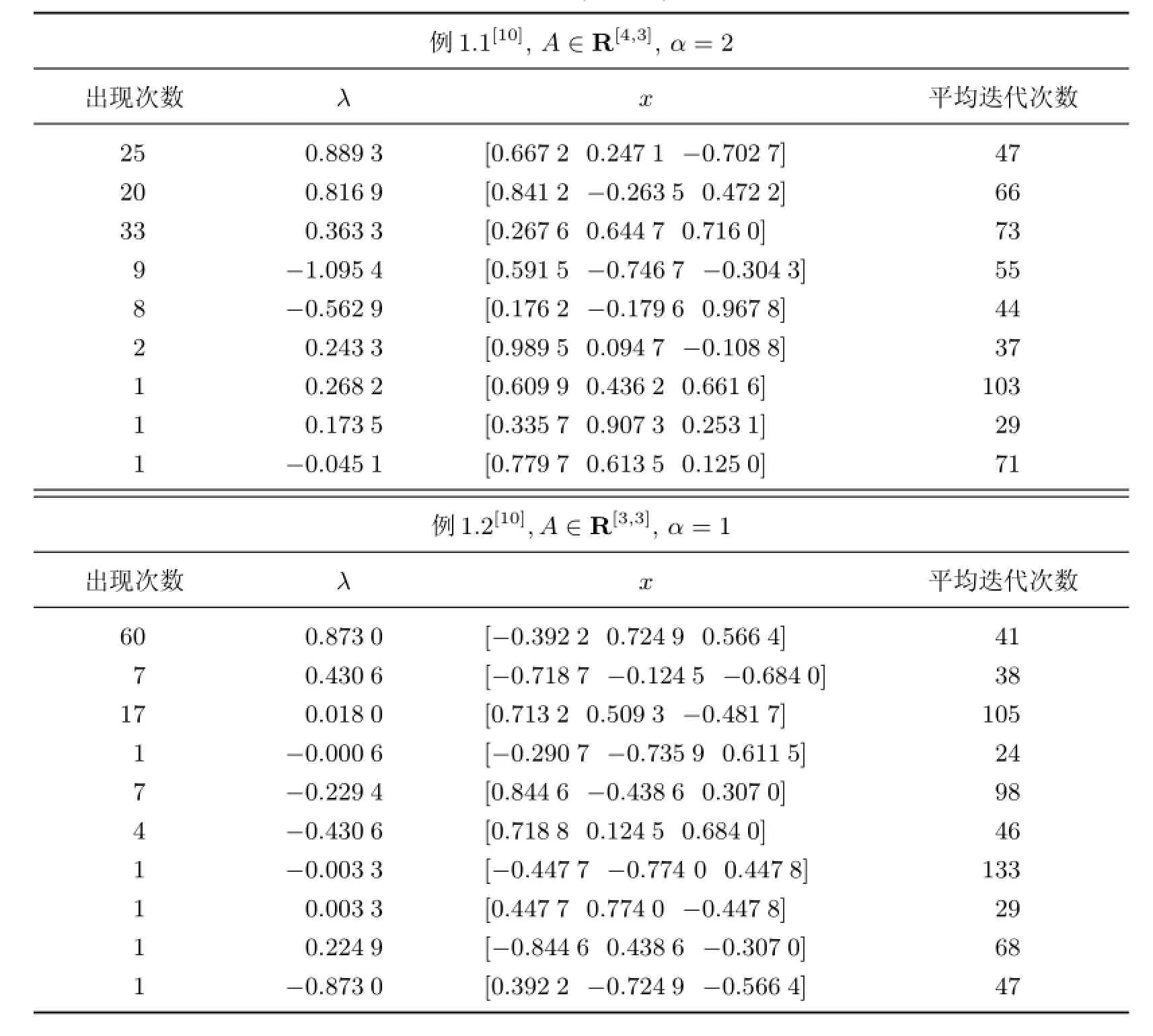
表2 由100個隨機初始點通過PSS-HOPM(凸)計算得到的特征值Table 2 Eigenvalues obtained by PSS-HOPM(convex)calculation of 100 random initial points

從表1和2的數值例子可以看出,本工作給出的PSS-HOPM可以算出比SS-HOPM更多的特征對(λ,x),且所用的時間沒有明顯的增加,其中SS-HOPM計算兩個例子的時間分別為0.315 718和0.197 564 s,PSS-HOPM計算兩個例子的時間分別為0.444 903和0.214 983 s.對于奇數階和偶數階對稱張量的情況,計算出的特征對均增加了6到7個,可見PSS-HOPM對于計算實對稱張量Z-特征值的效果非常明顯,其中Newton法預條件的計算精度ε1對算法的作用顯著.

[1]DIAMOND R.A note on the rotational superposition problem[J].Acta Crystallogr Sect A,1988, 44(2):211-216.

[2]DELATHAuWER L,DEMOOR B,VANDEWALLE J.On the best rank-1 and rank-(R1,R2,…,RN) approximation of higher-order tensors[J].SIAM J Matrix Anal Appl,2000,21(4):1324-1342.

[3]KOFIDIs E,REGALIA P A.On the best rank-1 approximation of higher-order supersymmetric tensors[J].SIAM J Matrix Anal Appl,2002,23(3):863-884.

[4]QI L.Eigenvalues and invariants of tensors[J].J Math Anal Appl,2007,325(2):1363-1377.

[5]QI L.Eigenvalues of a real supersymmetric tensor[J].J Symbolic Comput,2005,40(6):1302-1324.

[6]QI L.Rank and eigenvalues of a supersymmetric tensor,the multivariate homogeneous polynomial and the algebraic hypersurface it defnes[J].Journal of Symbolic Computation,2006, 41(2):1309-1327.

[7]LIM L H.Singular values and eigenvalues of tensors:a variational approach[C]//Proceeding of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing.2005:129-132.

[8]DuPONT T F,SCOTT L R．The power method for tensor eigenproblems and limiting directions of Newton iterates[J].Numerical Linear Algebra with Applications,2013,20(6):956-971.

[9]周會曉,倪勤,曾梅蘭.求實對稱張量Z-特征值的牛頓法[J].淮北師范大學學報(自然科學版), 2014,35(3):10-12.

[10]KOLDA T G,MAYO J R.Shifted power method for computing tensor eigenpairs[J].Siam J Matrix Anal,2010,32(4):1095-1124.

A preconditioning iterative algorithm for eigenvalue problem of symmetric tensor

GU Chuanqing,LI Long
(College of Sciences,Shanghai University,Shanghai 200444,China)

Shifted symmetric high order power method(SS-HOPM)is a well-known iterative algorithm for solving tensor Z-eigenvalue.In this paper,the Newton method is used to deal with the initial condition of the algorithm.A Newton preconditioning SS-HOPM (PSS-HOPM)for the symmetric tensor eigenvalue problem is obtained.Two numerical examples are used to illustrate that,compared with the SS-HOPM algorithm,this algorithm can calculate more eigenvalues with little increase of computation time.

shifted symmetric high order power method(SS-HOPM);Newton method; Newton preconditioned method

O 241

A

1007-2861(2017)01-0068-05

10.3969/j.issn.1007-2861.2016.07.009

2016-12-05

國家自然科學基金資助項目(11371243);上海市教委創新基金資助項目(13ZZ068);上海市重點學科建設資助項目(S30104)

顧傳青(1955—),男,教授,博士生導師,博士,研究方向為數值逼近、數值代數及其應用. E-mail:cqgu@shu.edu.cn