為什么引力如此微弱？隱藏的第五維度為你揭曉奧秘

麗薩·蘭道爾

希格斯玻色子只是大型強子對撞機所能發現的物質的冰山一隅，并非大型強子對撞機實驗的唯一搜尋目標。科學家研究弱尺度的最主要的原因，可能是沒有人認為希格斯玻色子是遺留的唯一問題。物理學家希望希格斯玻色子只是一個有著更多內涵的模型中的一個元素，而該模型可以告訴我們關于物質乃至時空本身更多的性質。

只存在希格斯玻色子而沒有其他新元素的事實導致了另一個巨大的謎團，即所謂的等級問題。等級問題關心的是，為什么粒子的質量（特別是希格斯粒子的質量）是其實際具有的那個數值。決定基本粒子質量的弱能量標度是另一個質量標度——決定引力強度的普朗克質量——的10-16。為什么引力比我們所知的其他基本作用力弱這么多？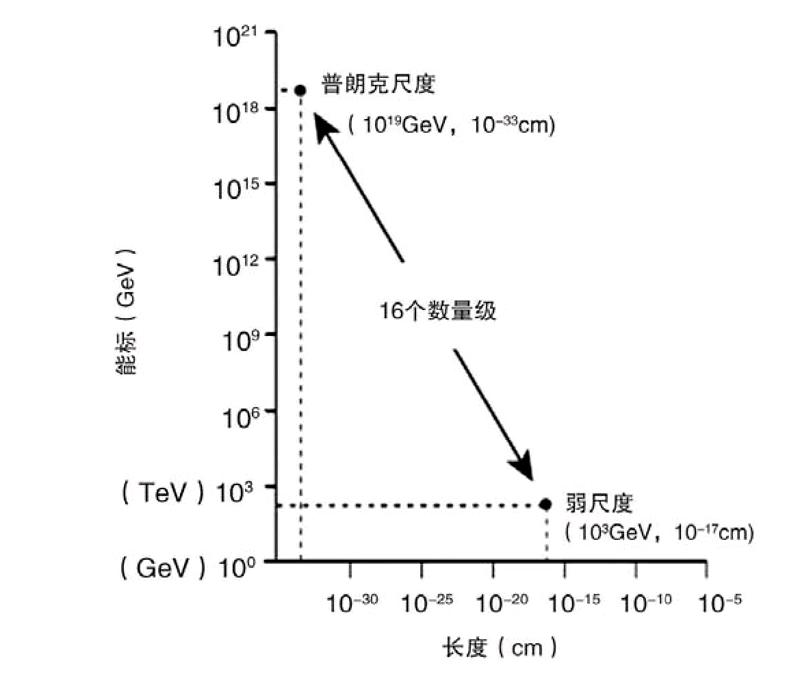

普朗克質量與弱作用的質量標度相差如此巨大，是引力如此微弱的原因。引力的相互作用依賴于普朗克質量的倒數。如果普朗克質量如我們所知的那樣巨大，引力必然極其微弱。

事實上，引力是迄今人們所知的最弱的相互作用力，之所以看起來沒有那么微弱，是因為整個地球的質量都在吸引著你。兩個電子之間的電磁力要比它們之間的引力大43個數量級。引力對基本粒子的作用完全可以忽略不計。

粒子物理學家不喜歡解釋大數字，比如普朗克質量與弱作用質量之比。但是該問題比僅從審美的角度反對神秘的大數字來得嚴重。根據量子場論（將量子力學與狹義相對論結合起來的理論），這里不應該有任何差別。對所有理論物理學家來說，解決等級問題的緊迫性都是不言而喻的。

在量子場論中，普朗克能標具有重要意義。不僅因為在該能標上引力變得極強，而且因為在此能標上引力與量子力學都至關重要，而我們已知的物理定律都失效了。然而，在低能標時，我們知道如何使用量子場論進行粒子物理學計算，而量子場論也做出了很多成功的預測，讓物理學家相信它是正確的。實際上，在所有科學領域中，測量值與預言值最符合的結果就來自量子場論。這樣的一致性絕非偶然。

當我們將相同原理應用于結合量子力學的虛粒子，并給出希格斯粒子的質量時，結果卻出人意料地混亂。理論上，任何粒子的虛效應似乎都可以給希格斯粒子一個與普朗克質量相當的質量。在這種情形下，弱相互作用伴隨的對稱性自發破缺的能標也將是普朗克能標，即比現在實驗能達到的能標高16個數量級。

我們認為，不同質量標度之間差異的等級問題，暗示了一個更大更好的基本理論。現在，還沒有一個簡單的模型可以完全給出該問題的答案。唯一有希望的方案是將標準模型擴展，使其包含一些顯著的性質。

我和拉曼·桑卓姆找到了一種看起來更好的方法，大多數物理學家都會同意其更有可能在自然中存在。請注意，這并不意味著大多數物理學家認為它是對的。許多人懷疑是否真的有人可以如此幸運，能正確預言大型強子對撞機將揭示的東西，或者給出一個無須更多實驗證據的、完全正確的模型。但是，作為一個占盡先機的想法，它很可能是正確的，并且與許多好的模型一樣呈現出清晰的策略，使得理論物理學家和實驗物理學家可以更全面地挖掘大型強子對撞機的可能性，甚至發現該方法的證明。

我和桑卓姆提出的模型只涉及一個額外維度，它的尺度不必很大，因此沒有引入新的涉及該維度尺度的等級。與大尺度額外維度的情況相反，宇宙的演化與最近的宇宙觀測自動相符。雖然我們的注意力只在這個單一的新維度上面，但是空間的其他附加維度還是可能存在的，只是在我們的模型中，在解釋粒子性質時，它們沒有發揮可以讓人察覺的作用。因此，當我們探究等級問題的答案時，為了配合有效理論的方法，可以合理地忽略這些維度，而只關注單一額外維度的效用。

如果我與桑卓姆的想法是正確的，那么大型強子對撞機很快就將給出關于時空本質的令人目眩的性質。原來，我們假設的宇宙是高度彎曲的，這與愛因斯坦提出的出現了物質與能量的時空的情形相符。其意思是，我們從愛因斯坦方程導出的幾何是“彎曲”的（這確實是一個預先存在的術語）。這意味著空間與時間隨著我們感興趣的那個單一額外維度的變化而發生改變。它改變的方式是：當你從額外維度的一個位置移動到另一個位置時，時空以及質量、能量都發生放縮。

彎曲時空幾何的一個重要結果是，雖然希格斯粒子的質量在額外維度的其他位置上變得很重，但是它在我們所處的位置上將具有弱尺度質量（和應該表現出的質量完全一致）。可能這聽起來具有任意性，其實不然。根據我們的模型，我們生活在一張膜，即弱膜上，而第二張膜（引力聚集的膜）被稱為引力膜，有些物理學家也把它稱為普朗克膜。這張膜包含一個從額外維度來看與我們隔離開來的宇宙。在這種情景中，第二張膜可能實際上恰好跟我們相鄰，只與我們相隔一個無窮小的距離——比如10-32米。

從彎曲幾何得出的最顯著的性質是引力子——傳遞引力的媒介粒子，它在另一張膜上的質量遠比在我們這張上的大。這將使得引力在額外維度的其他位置上很強，而在我們所處的這個位置上很弱。事實上，我和桑卓姆發現引力的強度在距離我們很近的地方比在另一張膜上小，并且呈指數級衰減，因此給出了引力如此微弱的一個解釋。

另一種解釋這個結果的方法是通過時空幾何，時空尺度依賴于第四個空間維度的位置。在這里，質量也呈指數函數縮放，這就使得希格斯玻色子的質量呈現出它需要的數值。雖然有人會爭辯說我們的模型依賴一個假設，即兩個巨大的、平坦的膜限定了額外維度的宇宙，但是一旦你給定由膜和被稱為“主體”的額外維度空間所承載的能量時，該幾何可以直接從愛因斯坦的引力理論中推導出來。當這樣做時，我們即可發現此前提到的幾何（即卷起來的彎曲空間）的質量按照

解決等級問題所需的方式進行縮放。

與大尺度額外維度模型不同，基于彎曲幾何的模型不會將老的等級問題換成新的等級問題（即為什么額外維度如此巨大）。在彎曲幾何中，額外維度并不大。巨大的數值來自一個呈指數縮放的空間和時間。指數縮放使得尺度以及質量的比例是一個巨大的數字，甚至當這些物體在額外維度中相隔不遠時，也是如此。

指數函數不是編造出來的，而是來自我們的模型中愛因斯坦方程的唯一解。我和桑卓姆計算得出，在彎曲幾何中引力與弱相互作用的比是兩張膜之間距離的指數函數。如果兩張膜的間隔是一個合理數值（幾十倍于引力設定的距離），那么質量與相互作用強度的正確等級就會自然出現。

在彎曲幾何中，我們受到的引力如此微弱的原因，不是由于它在大尺度額外維度中被弱化了，而是因為它被聚集到其他地方—另一張膜上。我們受到的引力由位于額外維度另一個位置的、某個很強的相互作用呈指數衰減的尾巴來決定。

我們之所以沒有看到位于另一張膜上的另一個宇宙，是因為這兩個世界共有的作用只有引力，而引力在我們附近已經太弱，以至于無法傳遞可以察覺的信號。事實上，這種情景可被當作一個多重宇宙的例子。在多重宇宙中，我們世界的物質和元素與另一個世界的物質之間的作用非常微弱，或者在某些情況下根本沒有相互作用。

然而，絕大多數猜想都不能被驗證，只能停留在想象的空間中。畢竟，如果物質如此遙遠，連從那里發出的光在宇宙有限的壽命中都不能到達地球，因此我們是無法探測到它的。不過，我和桑卓姆提議的多重宇宙的情景不是一般的提議，因為共有的引力可以導致實驗上可探測的結果。我們不是直接接觸另一個世界，而是在更高維度的內部空間中傳播的粒子來造訪我們。

大型強子對撞機即將展開的高能實驗可以幫助我們確定，額外維度僅僅是一個天馬行空的想法，還是一個關于宇宙的真實元素。如果我們的理論正確，那么我們可以預期大延伸閱讀型強子對撞機產生KK模式。因為與等級問題的聯系，我們的模型尋找KK模式所需的能標，大型強子對撞機是可以達到的。這一能標應該在萬億電子伏特的量級，即弱尺度能標上。一旦能量達到如此之高，這些重粒子就可能出現。KK粒子的發現將為我們提供關鍵的證據，給我們提供擴張的世界的

啟示。

事實上，彎曲幾何中的KK模式有一個重要且特別的性質。雖然引力子本身的強度極其微弱（畢竟它傳播的是極其微弱的引力），但它相互作用的KK 模式強得多——幾乎與弱作用的強度一樣，是引力強度的億萬倍。

KK引力子具有如此出人意料的相互作用強度的原因在于它們所處的彎曲幾何。由于時空強烈地彎曲，引力子KK模式的相互作用比我們感受到的引力子傳播的引力作用強得多。在彎曲幾何中，不僅質量被縮放，引力強度也被縮放。計算表明，在彎曲幾何中，KK引力子的相互作用強度可以與弱尺度上的粒子的相互作用相當。

這意味著不同于超對稱模型，也不同于大尺度額外維度模型，我們的模型的實驗證據不是來自有趣的粒子逃逸而造成的能量缺失。相反，該證據將是更干凈也更容易確認的信號——探測器中的粒子衰變成標準模型粒子時留下的可見軌跡（KK粒子產生并且衰變成電子—正電子對）。

這實際上就是目前實驗物理學家找尋所有新的重粒子的方法，他們并不能直接看到粒子，但可以觀測到那些粒子衰變之后的產物。從原則上說，這可以提供比缺失能量更多的信息。通過研究這些衰變產物的性質，實驗物理學家可以得出最初出現的粒子的性質。

如果彎曲幾何的情景是正確的，那么我們將很快看到KK引力子模式衰變出來的粒子對。通過測量末態粒子的能量、荷以及其他性質，實驗物理學家將可以推導出KK粒子的性質。這些鑒別特征以及粒子衰變成各種末態的比例，將有助于實驗物理學家斷定他們是否發現了KK引力子或者其他新的奇異元素。這些模型讓我們知道需要找尋的粒子的本質，也讓物理學家可以以此來分辨這

些可能性并做出預測。