在數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的思維能力
王桂英
(河北省鹽山縣第三中學(xué) 河北 鹽山 061300)
在數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的思維能力
王桂英
(河北省鹽山縣第三中學(xué) 河北 鹽山 061300)
數(shù)學(xué)教學(xué)中應(yīng)該重視學(xué)生思維能力的培養(yǎng),讓學(xué)生接受和記憶數(shù)學(xué)知識的同時(shí),引導(dǎo)學(xué)生抓住數(shù)學(xué)問題的本質(zhì),注重?cái)?shù)學(xué)知識間的相互滲透與遷移,真正吸收和消化知識,形成知識體系,活學(xué)活用數(shù)學(xué)知識,從而提高學(xué)生的思維能力。
數(shù)學(xué)教學(xué);思維能力;培養(yǎng)與提高
人類的一切活動(dòng)都離不開思維。思維能力就是我們遇到問題想辦法的過程。人的天性固然影響思維能力,但后天的教育與訓(xùn)練對人的思維能力影響更大、更深。因此,在教學(xué)中應(yīng)該重視學(xué)生思維能力的培養(yǎng)。比如,在初中數(shù)學(xué)教學(xué)中,不能只是讓學(xué)生接受和記憶數(shù)學(xué)知識,或是簡單的套用格式解題,應(yīng)該學(xué)透數(shù)學(xué)問題的本質(zhì),注重?cái)?shù)學(xué)知識間的相互滲透與遷移,真正吸收和消化知識,形成知識體系,進(jìn)而活學(xué)活用數(shù)學(xué)知識。在此,筆者結(jié)合數(shù)學(xué)教學(xué)實(shí)踐談?wù)勛约旱囊恍┳龇ā?/p>
1 引導(dǎo)學(xué)生把握數(shù)學(xué)概念和性質(zhì)的本質(zhì)提高思維能力
數(shù)學(xué)教學(xué)離不開概念教學(xué),教學(xué)時(shí)應(yīng)重視數(shù)學(xué)概念的生成過程,以此來鞏固學(xué)生對數(shù)學(xué)基礎(chǔ)知識的掌握,提高學(xué)生分析問題的能力。
例1:在學(xué)完角平分線概念后,出示如圖1的試題。將圖1中的直角C折疊,點(diǎn)C落在AB上的點(diǎn)E處,假如∠B=30,BC=15 cm,則DE=()cm。
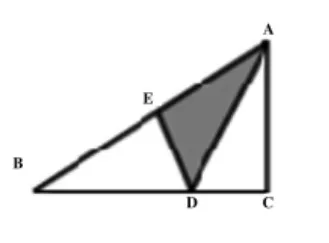
圖1
A、3 cmB、4 cmC、5 cmD、6 cm
從表面上來看,試題中的問題似乎與角平分線的性質(zhì)沒有直接關(guān)系,但試題對知識點(diǎn)考查的本質(zhì)并沒有變。從試題中“直角C折疊,點(diǎn)C落在AB上的點(diǎn)E處”得知AD實(shí)際上就是∠BAC的角平分線,里面包含了“角平分線”、“軸對稱”等概念和性質(zhì)。所以,答案很容易得出DE=5 cm。因此,在教學(xué)時(shí)不單單要求學(xué)生掌握概念和性質(zhì),重要的是引導(dǎo)學(xué)生把握他們的本質(zhì),從探究過程中培養(yǎng)學(xué)生的思維能力。
2 活學(xué)活用數(shù)學(xué)公式,培養(yǎng)學(xué)生的創(chuàng)新思維能力
數(shù)學(xué)中有無數(shù)的公式,牢記這些公式對解答數(shù)學(xué)題至關(guān)重要。但是死記硬背這些公式往往會抑制學(xué)生的思維。因此,在教學(xué)數(shù)學(xué)公式時(shí),要重視數(shù)學(xué)公式的推導(dǎo)過程,運(yùn)用多媒體創(chuàng)設(shè)情境,再現(xiàn)知識的形成過程,從學(xué)生已有知識的基礎(chǔ)上促成對新知識的建構(gòu),得出新的公式,這樣才有利于學(xué)生掌握公式的內(nèi)涵本質(zhì),從而靈活運(yùn)用數(shù)學(xué)公式。
例2:已知a+b=4,a2+b2=4,求a2b2的值?例3:已知a+b=4,ab=2,求a4+b4的值?例4:已知x-1/x=3,求x2-1/x2和x4-1/x4的值?仔細(xì)分析以上3道數(shù)學(xué)試題,其本質(zhì)實(shí)際上都是考查學(xué)生對完全平方公式靈活運(yùn)用的問題。學(xué)生只要掌握了所學(xué)的數(shù)學(xué)知識,靈活運(yùn)用所學(xué)的數(shù)學(xué)公式,解決以上一系列問題輕而易舉。在數(shù)學(xué)教學(xué)中,不僅要讓學(xué)生記住公式,更重要的是引導(dǎo)學(xué)生將公式活學(xué)活用并進(jìn)行創(chuàng)新使用,只有這樣,學(xué)生的發(fā)現(xiàn)能力和創(chuàng)造性思維能力才會得到進(jìn)一步的提升。
3 緊抓問題的內(nèi)在聯(lián)系和關(guān)鍵點(diǎn)提高學(xué)生邏輯推理的思維能力
提高學(xué)生的數(shù)學(xué)思維能力是初中數(shù)學(xué)的教學(xué)目標(biāo)之一,要實(shí)現(xiàn)這一目標(biāo),就要培養(yǎng)學(xué)生的邏輯推理能力。所以,在平時(shí)的數(shù)學(xué)解題訓(xùn)練中,通過“同中求異”、“異中求同”等多角度的訓(xùn)練,來挖掘問題的內(nèi)在聯(lián)系,從表面現(xiàn)象挖掘出問題的實(shí)質(zhì),使學(xué)生的邏輯推理能力逐步得到提升。
例5:已知:三角形周長為60,三條邊a∶b∶c =3∶4∶5,求三角形的三條邊各是多長?
解法1:依題意得出a+b+c=60,a∶b∶c= 3∶4∶5,運(yùn)用解方程的辦法求解。
解法2:假設(shè)a=3x,那么b=4x,c=5x;先求得x,然后各邊的長即求出。
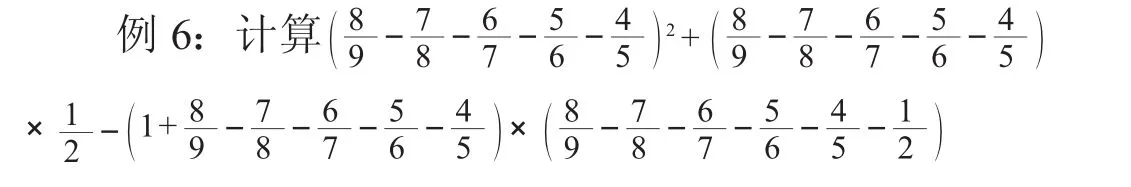
解法1:按照先通分,然后按分?jǐn)?shù)的加減法運(yùn)算求值。

對于該題,直接用分?jǐn)?shù)通分的加減法運(yùn)算求值顯然很費(fèi)勁。解法2引導(dǎo)學(xué)生觀察括號內(nèi)的分?jǐn)?shù)算式是相同的,故可以采用換元法解題輕松自如。
以上問題的解答過程不僅從多角度來思考問題,而且注重了問題與問題之間的內(nèi)在聯(lián)系,這有利于邏輯思維能力的培養(yǎng)。

