充填管道堵塞風險性的SPA-AHP綜合評價

趙麗軍

(甘肅廠壩有色金屬有限責任公司廠壩鉛鋅礦， 甘肅 隴南市 742504)

充填管道堵塞風險性的SPA-AHP綜合評價

趙麗軍

(甘肅廠壩有色金屬有限責任公司廠壩鉛鋅礦， 甘肅 隴南市 742504)

為了預測充填管道堵塞風險性大小，建立充填管道堵塞風險性的評價系統和評價等級標準。基于層次分析法(AHP)，對各評價指標賦予不同的權重，引入集對分析法(SPA)，對充填管道風險性進行定量分析。運用該評價模型對金川龍首礦、貢北金礦、河東金礦、開陽磷礦4個代表性礦山的充填管道輸送系統進行驗證，貢北金礦、河東金礦充填管道堵塞風險性等級為2級“風險一般”，金川龍首礦、開陽磷礦的風險性等級為3級“風險較大”，評價結果符合礦山實際情況，表明該模型具有較高的評價精度，且合理、科學，可推廣至同類礦山應用。

充填系統；管道輸送；管道堵塞；評價模型；集對分析

0 引 言

隨著淺部資源的消耗殆盡，礦山開采向深部邁進的趨勢勢不可擋，然而深部開采面臨的“三高一擾動”問題日益嚴峻，尤其是高地壓的控制，因此為了更好的控制深部的高地壓，充填采礦法被金屬礦山廣泛的使用[1]。充填系統的順暢運轉是充填充填采礦法成功實施的基本保障，而其子系統管道運輸系統作為薄弱環節之一經常面臨磨損、堵塞、爆裂等失效事故，其中以堵塞事故對充填管道的威脅最大。所以，對充填管道堵塞風險性進行評價，有助于礦山提前采取防范措施，為此，國內外學者提出很多評價模型對其進行評價。王新民等建立了基于未確知理論的充填管道堵塞風險預測模型[2]；張欽禮等利用熵權和模糊數學理論建立了充填管道堵塞風險評價模型[3]。

1989年，趙克勤提出了集對分析(SPA)數學理論。SPA理論主要用于分析系統內確定和不確定性之間的相互作用[4]，尤其是在不確定問題分析方面優點突出。目前，礦山系統安全評價[5]、水文地質情況評估[6￣8]、人工智能操作[9￣10]、自然災害誘因分類[11]、工程圍巖質量分級[12￣13]、邊坡穩定性分析[14￣15]和采場頂底板、兩幫穩定性評價[16￣17]、可爆性分級[18]等領域都廣泛應用了該理論。充填管道堵塞風險性動態分析和評價是一項涉及多指標的研究領域，SPA理論在確定復雜系統內多指標對結果影響的權重方面顯得辦法不多，缺陷明顯。層次分析 (AHP)是一種將系統指標條理層次化并對指標賦予不同權重的數學方法[19￣21]。通過分析，可以將SPA和AHP兩種方法相結合建立AHP-SPA綜合評價模型，并利用上述模型評價不同礦山充填管道堵塞風險[22]，為礦山提供防范充填堵塞措施等級。

1 SPA-AHP模型

1.1 SPA-AHP原理

SPA理論的核心是把研究對象當作一個確定-不確定系統 (NY系統)。 NY系統是由集合A、集合B組成的集對H(A,B)，而對集對H(A,B)從特性、關系、結構、狀態、趨勢，以及相互聯系模式進行分析并可定量表達NY系統，得到集合A和B的聯系度表達式：

(1)

式中：N——集對H(A,B)的所有特性；

S——集合A、B共有的特性；

P——集合A、B對立的特性；

F——集合A、B既不共有也不對立的特性；

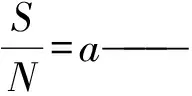
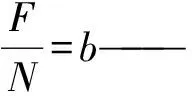
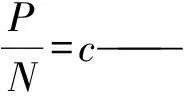
i——差異度系數，取值范圍為[-1,1]；

j——對立度系數，一般取值-1。

基于SPA理論分析具體問題時，集對的特性多且復雜，難以考慮特性之間的關系及特性導致問題發生的概率大小，即權重。因此，借助AHP確定特性權重是一種合理的簡化方式。假設，特性為S的權重為wn(n=1,2,...，s)，特性為F的權重為wm(m=1,2,...，f)，特性為P的權重為wl(l=1,2,...，p)，則考慮特性權重后的聯系度表達式為：

(2)

1.2 SPA-AHP步驟

(1) 建立充填管道堵塞指標系統。導致礦山充填管道堵塞的因素很多，根據礦山充填實際和前人研究成果確定了以下主要評價指標：充填料漿體積分數(I1)、充填料漿的密度(I2)、充填管道的絕對粗糙度(I3)、管道內徑(I4)、充填倍線(I5)、偏斜率(I6)、料漿流速與臨界流速之比(I7)、加權平均粒徑(I8)、充填骨料形狀(I9)及充填料漿的腐蝕性(I10)。

(2) 利用AHP法確定指標權重。兩兩比較指標的重要性，建立判斷矩陣A=(aij)，即當前指標與相鄰上一層指標的重要性判斷矩陣，計算判斷矩陣A=(aij)的最大特征根λ和特征向量W，計算得到的特征向量W經歸一化處理后，可以作為充填管道堵塞指標的權重Wa。

(3) 充填管道堵塞風險性等級標準。結合工程經驗類比，根據導致充填管道堵塞指標的含義與作用，建立了以下四類管道堵塞風險性評價等級：1級 (堵塞風險性很小)、2級 (堵塞風險性一般)、3級 (堵塞風險性較大)和4級 (堵塞風險性很大)，具體評價標準見表1。

(4) 基于SPA理論對充填管道堵塞風險性評價。根據式(2),計算充填管道堵塞風險性的聯系度μ，μ∈[-1,1]。首先利用“均分原則”確定差異度系數i，假設μ為d元聯系數，則將區間[-1,1]劃分為d-1等份，其等份點值從左至右記為：J,Id-2，Id-3，...,I1。再根據“均分原則”將區間[-1,1]劃分為d等份，從左至右各子區間對應評價等級1,2,...,d，從而μ值位于某個區間，其評價等級即為該區間所對應的評價等級。

2 工程實例評價

以金川龍首礦、貢北金礦、河東金礦、開陽磷礦為充填管道堵塞風險性的評價對象，各礦山導致充填管道堵塞的指標實測數據見表2，建立SPA-AHP綜合評價模型，對各礦山充填管道系統的堵塞風險性進行評價。

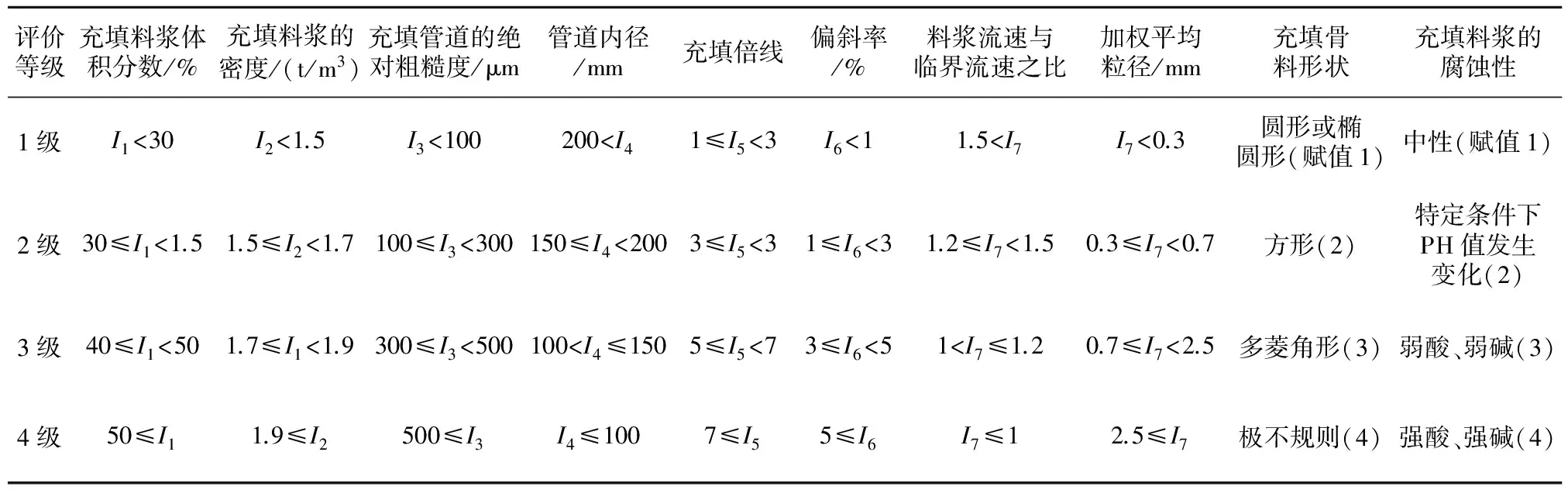
表1 評價等級標準取值范圍

表2 礦山指標實值

2.1 確定指標權重

根據層次分析法原理建立判斷矩陣A，如下式所示，以此確定指標權重。

根據A，可得權重向量W1=(0.1500，0.1500，0.0345，0.1500，0.0460，0.0193，0.1500，0.0750，0.0750，0.1500)。經一致性檢驗公式計算得CR=0.004<0.100，滿足檢驗標準。

2.2 計算聯系度

根據指標實值和權重，得金川龍首礦的聯系度μ1=0+0.4403i1+0.1845i2+0.375j。根據“均分原則”和μ為四元聯系數，區間[-1,1]的等份點值從左至右為：-1，-0.333，0.333，1。確定i2=-0.333，i1=0.333，從而計算出μ1=-0.2898，同理可得貢北金礦、河東金礦、開陽磷礦的聯系數分別為μ2=0.1388,μ3=0.1026,μ4=-0.1668。

2.3 評價結果

根據“均分原則”，將區間[-1,1]劃分為4等份(-1，-0.5)，(-0.5，0)，(0，0.5)，(0.5,1)，分別對應評價等級的4級“風險很大”、3級“風險較大”、2級“風險一般”、1級“風險很小”，可知μ1∈(-0.5,0)，因此，可知貢北金礦、河東金礦充填管道堵塞風險性等級為2級“風險一般”，金川龍首礦、開陽磷礦充填管道堵塞風險性等級為3級“風險較大”。

3 結 論

基于SPA-AHP可以有效進行充填管道堵塞風險性評價，在確定10項導致主要充填管道堵塞因素指標的基礎上，建立了充填管道堵塞的評價等級標準，選取充填系統較為成熟的金川龍首礦、貢北金礦、河東金礦、開陽磷礦4個代表性礦山對評價模型進行驗證，通過層次分析法確定指標權重，進而基于集對分析理論得到各礦山的評價等級：金川龍首礦、開陽磷礦為3級“風險較大”，貢北金礦、河東金礦為2級“風險一般”，評價結果較為符合礦山實際，從而充填管道堵塞風險性評價提供了一個新的途徑。

[1]王新民,古德生,張欽禮.深井礦山充填理論與管道輸送技術[M].長沙：中南大學出版社，2010:1￣6.

[2]王新民,高瑞文,胡 威,等.充填管道堵塞風險預測模型[J].中南大學學報(自然科學版),2013，44(11):4604￣4610.

[3]張欽禮,曹瑞峰,王 石，等.基于熵權和模糊數學的充填管道堵塞堵塞風險評價[J].科技導報,2013，31(28):30￣34.

[4]趙克勤.集對分析及其初步應用[M].杭州：浙江科學技術出版社，2000.

[5]鄭賢斌,陳國明.基于SPA安全綜合評價方法及其應用[J].哈爾濱工業大學學報,2006，38(2):290￣293.

[6]王宏偉,張 鑫,邱俊楠.模糊集對分析法在水資源安全評價中的應用[J].西北農林科技大學學報(自然科學版),2011，39(10):209￣214.

[7]何菡丹,王 棟.基于小波消噪與秩次集對分析的水文時間序列預測[J].南京大學學報(自然科學版),2012，48(6):736￣745.

[8]劉銀迪,張小壯,張澤中.序位集對分析在遼河流域年降雨預測中的應用[J].安徽農業科學,2011，39(28):17534￣17536.

[9]趙克勤.SPA的同反異系統理論在人工智能研究中的應用[J].智能系統學報,2007，2(5):20￣35.

[10]趙克勤.集對分析的不確定性系統理論在AI中的應用[J].智能系統學報,2006，1(2):16￣25.

[11]王文圣,金菊良,李躍清.基于集對分析的自然災害風險度綜合評價研究[J].四川大學學報(工程科學版),2009，41(6):6￣12.

[12]王迎超,徐興華,劉永莉,等.公路隧道圍巖分級的集對分析模型[J].哈爾濱工業大學學報,2011，43(4):114￣119.

[13]申艷軍,徐光黎,張亞飛,等.基于集對分析的可拓學方法在地下硐室圍巖分類中的應用[J].地質科技情報,2010，29(5):125￣130.

[14]秦植海,秦 鵬.高邊坡穩定性評價的模糊層次與集對分析耦合模型[J].巖土工程學報,2010,32(5):706￣711.

[15]劉 曉,唐輝明,劉 瑜.基于集對分析的滑坡變形動態建模研究[J].巖土力學,2009,30(8):2371￣2378.

[16]李同鎖,何啟林.基于集對分析的采煤工作面頂板穩定性評價[J].煤炭工程,2010,32(5):706￣711.

[17]鄭海力,童陽春.基于模糊集對與優勢關系粗糙集的巷道穩定性系統化分析[J].礦業研究與開發,2016,36(07):86￣92.

[18]錢 立,王文杰,潘春艷,等.基于綜合賦權集對分析方法的巖體可爆性分級研究與應用[J].化工礦物與加工,2015(11):37￣40.

[19]王新民,趙 彬,張欽禮.基于層次分析和模糊數學的采礦方法選擇[J].中南大學學報(自然科學版),2008,39(5):875￣880.

[20]宋霞飛,王志勇.基于集對分析同一度的采礦方法最優選擇[J].采礦技術,2014,14(03):12￣15.

[21]王新民,劉賤剛,張欽禮.基于信息熵層次集評價方法的采礦方案選擇[J].化工礦物與加工,2011(07):18￣21，25.

[22]王新民,王 石,鄢德波,等.基于未確知測度理論的充填管道堵塞風險性評價[J].中國安全科學學報,2012(04):151￣156.

2016￣10￣27)