K均值聚類自適應零速檢測人員定位技術*

孫 偉，丁 偉，閆慧芳

(遼寧工程技術大學測繪與地理科學學院，遼寧阜新123000)

K均值聚類自適應零速檢測人員定位技術*

孫 偉*，丁 偉，閆慧芳

(遼寧工程技術大學測繪與地理科學學院，遼寧阜新123000)

零速區(qū)間檢測準確度直接制約著零速修正算法對于改善人員定位系統(tǒng)提供位置精度的能力。針對現(xiàn)有零速檢測方案存在閾值設定以及訓練模型準確性等問題，提出一種基于加速度幅值滑動方差開展行走步態(tài)零速區(qū)間檢測方法，采用K均值聚類方法自適應糾正初始檢測結果中的誤檢狀態(tài)，構造Kalman濾波器并在零速區(qū)間以慣性系統(tǒng)解算的速度信息為觀測量進行量測更新來限制導航誤差積累。開展人員多種運動狀態(tài)下的行走測試，實驗結果表明K均值聚類自適應算法能對零速區(qū)間進行有效地檢測，獲取的位置解算誤差小于2%。

人員定位;K均值聚類;Kalman濾波;零速修正

相對其他室內人員定位系統(tǒng)而言，基于MEMS的定位系統(tǒng)無需預先設置節(jié)點，完全依靠固定在行人身上的微慣性測量單元 MIMU(Micro Inertial Measurement Unit)輸出信息進行位置推算，具有較高的自主性［1－3］。但慣導系統(tǒng)的定位誤差隨時間三次方增長成為制約其應用時間和應用范圍的主要因素［4］。對微慣性人員定位系統(tǒng)而言，零速區(qū)間檢測準確程度是實施Kalman濾波及時清零速度誤差并修正位置誤差的前提［5－8］。人員行走過程中，其腳步運動具有周期特征，這一規(guī)律將反映到傳感器輸出數(shù)據(jù)上［9］。文獻中已有檢測算法可分為兩類，第1類算法直接根據(jù)傳感器輸出數(shù)據(jù)通過設定閾值進行判斷，利用的檢測量包括加速度模值、角速率模值、加速度滑動方差、角速率能量等，這類方法計算簡單，對特定行走步態(tài)的零速區(qū)間能做出較為準確的判斷，但需要設定固定閾值［10］。因此對不同個體、不同運動狀態(tài)適應性較差。第2類算法根據(jù)機器學習相關理論對原始數(shù)據(jù)進行分析判斷，包括樸素貝葉斯分類、支持向量機(SVM)分類、隱馬爾科夫模型(HMM)等，這類算法對不同運動狀態(tài)有良好的適應性，但前提需要進行大量實驗并利用包含各種運動狀態(tài)的數(shù)據(jù)訓練模型，因此算法復雜度高且依賴模型好壞程度［11－13］。本文以加速度滑動方差為檢測量，通過閾值法得到初始分類結果后，統(tǒng)計各次靜態(tài)、動態(tài)持續(xù)長度，然后利用K均值聚類將初始分類靜、動態(tài)分別聚為兩類，根據(jù)聚類性能自適應糾正初始檢測結果得最終檢測零速區(qū)間，并通過Kalman濾波約束慣導解算誤差發(fā)散保證導航位置的可靠性和準確性。

1 定位算法編排

MEMS行人定位系統(tǒng)編排如圖1所示。

圖1 行人導航系統(tǒng)框圖

1.1 初始對準

慣性導航系統(tǒng)在進入正式工作狀態(tài)之前需要進行初始對準獲取初始捷聯(lián)矩陣Cnb，人員定位系統(tǒng)開始航位推算前雙腳處于站立狀態(tài)靜止一段時間，此時MIMU只受重力影響，加速度計輸出為重力在載體系的投影。以東北天(ENU)地理系為導航系，右前上(RFU)為載體系，則有

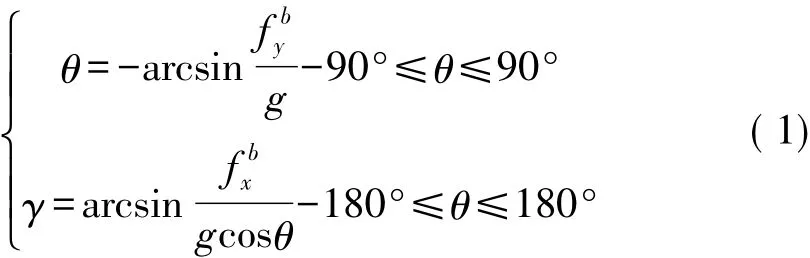
利用式(1)可求得俯仰角θ和橫滾角γ，而方向位角ψ可利用MIMU中的磁強計確定［14］。

式中:cx、sx分別表示cosx、sinx(x=θ、γ)。磁方位角ψm與地理方位角ψ之間相差一個與緯度B有關的磁偏角α(可由世界地磁模型 WMM2015計算得到)［15－16］，所以

1.2 慣性解算

1.2.1 姿態(tài)更新

采用四元數(shù)微分方程進行系統(tǒng)姿態(tài)更新［4］

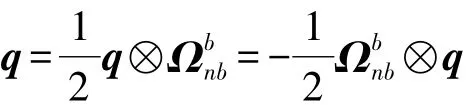
式中:RM、RN分別為地球子午圈曲率半徑和卯酉圈曲率半徑，B為緯度，h為高度。

對人員定位系統(tǒng)，由于人行走速度低，一般不超過1.4 m/s，最快不超過2.5 m/s，即使奔跑，也極少有人速度能達到10 m/s［17－18］。與之對應的ωnen的分量在10－7rad/s量級，且 ωnie的分量為10－6rad/s量級，因此可忽略這兩項

進而可得四元數(shù)更新解析式:

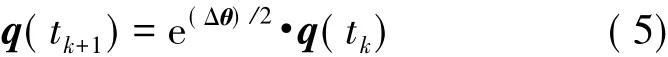
式中:q(tk)、q(tk+1)分別對應當前時刻及下一時刻姿態(tài)四元數(shù)，Δθ為區(qū)間［tk，tk+1］內ωbib引起的角增量矩陣，

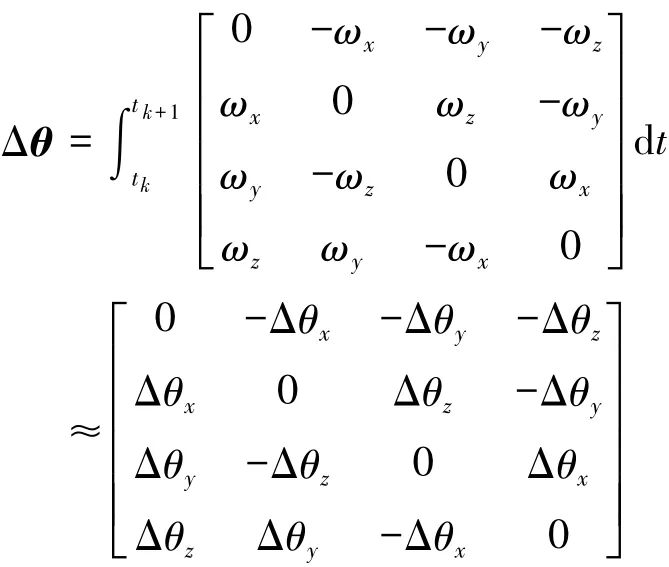
式中:ωx、ωy、ωz表示ωbib的3個分量。

將式(5)泰勒展開并取一階得到姿態(tài)更新數(shù)值計算公式

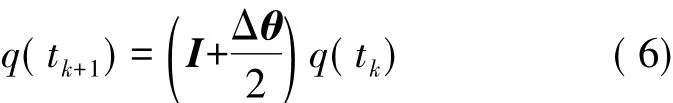
式中:I為四階單位陣。

1.2.2 速度更新

令vn=［vnEvnNvnU］T為導航系下速度矢量，則導航系下速度更新微分方程為［4］

忽略上式中哥氏加速度項－(2ωnie+ωnen)×vn的影響。進而由矩形積分可得速度更新數(shù)值計算公式

式中:vn(tk)、vn(tk+1)分別對應當前時刻及下一時刻的速度矢量，Δt為速度更新周期。

1.2.3 位置更新

傳統(tǒng)慣性導航系統(tǒng)位置更新通常采用經(jīng)緯度和大地高作為位置更新微分方程參量，該方法優(yōu)點是通過更新計算可直接獲得載體實時地理位置。而對于人員定位系統(tǒng)而言，人行走速度較低且MEMS慣導系統(tǒng)采樣率高，導致在更新周期內由行走引起的經(jīng)緯度位置變化非常小，不利于數(shù)值計算，因此將人員位置更新采用以ENU 3個方向相對位置表示的位置更新微分方程

式中:rn=［rnErnNrnU］T為相對位置矢量。

位置更新計算 tk+1時刻位置時，tk時刻速度vn(tk)及tk+1時刻速度vn(tk+1)都已求得，因此解上述位置更新微分方程可采用梯形積分得

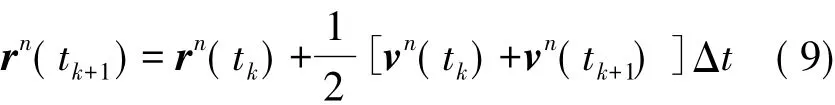
式中:rn(tk)、rn(tk+1)分別對應當前時刻及下一時刻的位置矢量。

2 K均值聚類零速檢測

2.1 初始檢測

初始檢測利用加速度滑動方差與設定閾值比較得初始零速區(qū)間。加速度滑動方差按下式計算:

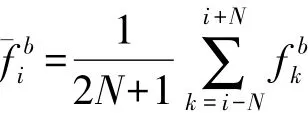
式中:2N+1為窗口大小，由加速度計采樣頻率確定。將計算出的加速度滑動方差與設定閾值比較，小于閾值的點即為靜止狀態(tài)的點。

2.2 檢測結果優(yōu)化

加速度滑動方差閾值法步態(tài)檢測結果中存在誤判導致步伐處于擺動過程中可能出現(xiàn)短時偽靜態(tài)，而在靜止過程中出現(xiàn)短時偽動態(tài)。針對如上問題通過設定閾值，將小于該閾值的短時狀態(tài)修正為其相反的狀態(tài)，即偽動態(tài)修正為靜態(tài)，或偽靜態(tài)修正為動態(tài)。本文利用K均值聚類方法根據(jù)各次狀態(tài)持續(xù)長度分別將靜態(tài)、動態(tài)自動聚類成兩類。記錄初始檢測結果中各次靜態(tài)(或動態(tài))持續(xù)長度構成序列L={l1，l2，…，ln}，然后設定兩個聚類簇 C={C1，C2}，得到聚類的目標是最小化平方誤差［19］

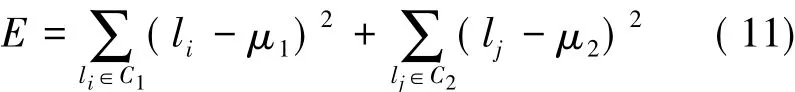
按式(11)分別對初始檢測結果靜、動態(tài)聚類成兩類，初始檢測時的閾值設定不當引起靜、動態(tài)各自聚類的效果不同。為此引入反映聚類性能度量的內部指標——Dunn指數(shù)(Dunn Index，DI)［19］

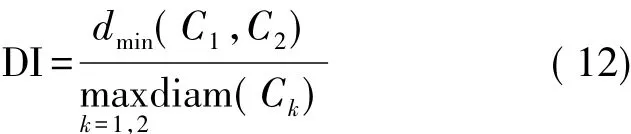
DI值越大則聚類性能越好。其中，dmin(C1，C2)=表示簇C1與簇C2最近樣本間的距離;表示簇 Ck(k=1，2)內樣本間的最遠距離。

初始檢測步態(tài)糾正方案如下:首先對初始檢測靜、動態(tài)分別聚類，然后計算聚類性能 DIStance和DISwing，最后選擇DI值較大的聚類將對應的偽狀態(tài)糾正為相反狀態(tài)。若靜態(tài)聚類效果優(yōu)于動態(tài)聚類效果(DIStance＞DISwing)，則依據(jù)靜態(tài)聚類結果對初始檢測結果進行糾正，將聚類所得短時靜態(tài)糾正為動態(tài)。

3 Kalman濾波零速修正

零速修正Kalman濾波是在非零速區(qū)間只進行時間更新，按慣導原理計算導航參數(shù)，由于MEMS陀螺測量數(shù)據(jù)存在誤差量大，導致慣性解算位置誤差以時間的三次方增長;在零速區(qū)間進行完整時間和量測更新，采用的量測量為慣導解算速度與零的差值，即假設零速區(qū)間行人腳步速度為零。由于行走特點及數(shù)據(jù)擾動，導致腳步速度在零速區(qū)間并不絕對為零，因此零速區(qū)間采用的這一偽觀測量同樣存在具有隨機性且不隨時間累積的誤差。閉環(huán)Kalman濾波綜合利用帶誤差的慣導解算數(shù)據(jù)及帶誤差的速度偽觀測量得出導航參數(shù)誤差的最優(yōu)估計，進而實現(xiàn)導航參數(shù)的閉環(huán)修正。

3.1 微慣性人員定位系統(tǒng)誤差方程

3.1.1 姿態(tài)誤差方程

令Φn=［xyz］T表示失準角，則捷聯(lián)慣導系統(tǒng)姿態(tài)誤差方程為

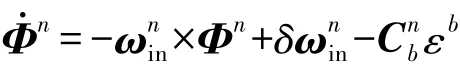
由前面分析可知，在人員定位系統(tǒng)中ωnin為極小量，因此上式中－ωnin×Φn項及δωnin項均為極小量，忽略這兩項可將姿態(tài)誤差方程簡化為

式中:εb為載體系下陀螺常值漂移，Cnb為姿態(tài)矩陣，在捷聯(lián)計算姿態(tài)四元數(shù)更新后由下式計算實時獲得

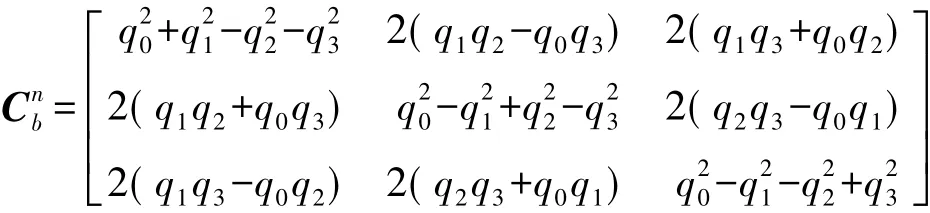
3.1.2 速度誤差方程

令δvn=［δvnEδvnNδvnU］T表示速度誤差，得到慣導系統(tǒng)速度誤差方程:

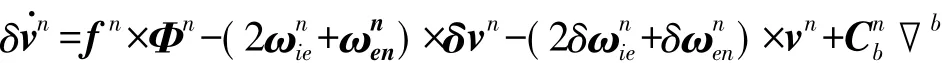
同樣由分析可知上式中－(2ωnie+ωnen)×δvn項及－(2δωnie+δωnen)×vn項均為極小量，因此忽略小量后MEMS人員定位系統(tǒng)速度誤差方程簡化為

3.1.3 位置誤差方程

令δrn=［δrnEδrnNδrnU］T表示位置誤差，則以相對位置矢量rn為基礎的MEMS人員定位系統(tǒng)位置誤差方程為

3.2 Kalman濾波器設計

根據(jù)MEMS人員定位系統(tǒng)誤差方程設計閉環(huán)Kalman濾波狀態(tài)方程

式中:X=［(Φn)T(δvn)T(δrn)T(b)T(εb)T］T為 Kalman濾波狀態(tài)向量;W=［(wbg)T(wba)T01×9］T為系統(tǒng)噪聲向量，其中wbg=［wgwgwg］T為陀螺白噪聲向量，wba=［wawawa］T為加速度計白噪聲向量;F為狀態(tài)轉移矩陣

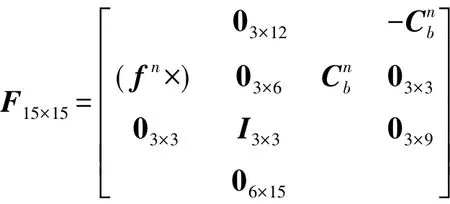
式中:(fn×)為加速度矢量fn對應的反對稱矩陣。

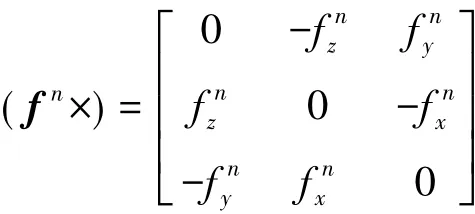
假定零速區(qū)間行人腳步速度為零，取該區(qū)間內微慣性系統(tǒng)計算速度與零的差值為偽觀測量，即令Z=vn，則可設計Kalman濾波零速修正的觀測方程

式中:H=［I3×303×12］為觀測矩陣。

4 實驗結果與分析

利用荷蘭Xsens公司生產的MTi－G－710開展多組人員行走實驗，將傳感器固定在鞋面。綜合考慮數(shù)據(jù)量和解算精度兩方面因素設置采樣率為100 Hz，采集三軸陀螺、三軸加速度計和三軸磁強計數(shù)據(jù)。實驗開始前保持腳面靜止5 s，以便系統(tǒng)完成初始對準，對于閉合行走軌跡，行走終點要求與起點重合。實驗過程中所采用的MEMS器件參數(shù)如表1所示。

表1 慣性器件參數(shù)

4.1 步態(tài)檢測實驗

為驗證步態(tài)檢測方法有效性，選取長距離行走數(shù)據(jù)進行實驗驗證。計算加速度滑動方差的窗口寬度設定為10，對應0.1個采樣周期也即0.1 s的數(shù)據(jù)，閾值設定為2 m2/s4。初始步態(tài)檢測將加速度滑動方差小于閾值的點置為靜態(tài)(狀態(tài)0)，大于閾值的點置為動態(tài)(狀態(tài)1)。然后利用K均值聚類將初始檢測靜、動態(tài)分別聚類成兩類(如圖2)。分別按式(12)計算兩類聚類的性能指標 DIStance=1.12、DISwing=0.25，即靜態(tài)聚類效果優(yōu)于動態(tài)聚類，對比圖2得出相同結論。因此，可根據(jù)DI值自動選定步態(tài)糾正方案，對于本實驗即為利用靜態(tài)聚類結果將假靜態(tài)糾正為動態(tài)。

圖2 初始檢測步態(tài)K均值聚類

利用加速度滑動方差閾值法檢測步態(tài)結果及經(jīng)K均值聚類糾正后步態(tài)檢測結果如圖3所示，對比兩種檢測結果表明僅依靠加速度滑動方差閾值法檢測步態(tài)中包含較多短時假靜態(tài)，而經(jīng)K均值聚類糾正后的步態(tài)修復了這些假靜態(tài)，檢測結果更加合理。

圖3 糾正前后步態(tài)檢測結果對比

4.2 不同路徑行走實驗

為驗證自適應步態(tài)檢測零速修正算法對人員位置解算的精度，分別開展圓形及400 m跑道閉合行走實驗。采用本文提出自適應零速修正融合閉環(huán)Kalman濾波算法解算位置變化，結果分別如圖4所示。

圓形行走軌跡為直徑34 m的小廣場花壇，逆時針繞花壇一圈并回到起點，解算位置結果如圖4所示。最終閉合效果較好，終點平面位置誤差2.023 2 m，相對行走路徑總長106.814 2 m的相對誤差為1.89%。

圖4 圓形行走軌跡

400 m跑道行走軌跡為足球場橡膠跑道最外道，逆時針繞跑道一圈后回到起點，其位置解算曲線如圖5。由于行走距離較長，由器件誤差引起的位置解算誤差隨時間逐漸增加，導致該長距離行走最終位置平面誤差為6.253 1 m，相對誤差為1.56%。

圖5 400 m跑道行走軌跡

不同運動軌跡下的位置誤差如表2所示。數(shù)據(jù)結果表明行走實驗的解算位置誤差雖然隨行走距離增大而增加，但其相對誤差均不超過2%，該結果對于采用單一MEMS慣導系統(tǒng)而言可滿足實際人員定位需求。

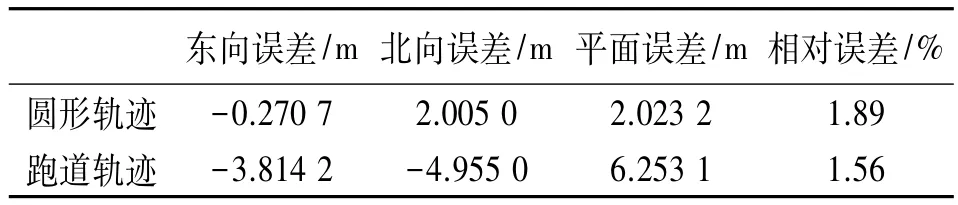
表2 位置誤差

5 結論

零速區(qū)間的有效檢測是零速修正算法得以準確應用的基礎，論文提出一種基于K均值聚類自適應零速修正的微慣性人員定位方法，通過簡化慣導方程并建立微慣性人員定位解算方法，論證加速度滑動方差閾值法結合K均值聚類自適應檢測零速區(qū)間的有效性。建立閉環(huán)Kalman濾波修正模型實現(xiàn)人員位置解算的零速修正。實驗結果表明，論文提出的自適應步態(tài)檢測方法顯著提高零速區(qū)間檢測的準確度，得到的位置解算相對誤差優(yōu)于2%，該測試結果可滿足小范圍內人員定位精度需求。

［1］ 張金亮，秦永元，梅春波.基于MEMS慣性技術的鞋式個人導航系統(tǒng)［J］.中國慣性技術學報，2011，19(3):253－256.

［2］ 孫偉，李婉秋，初婧，等.基于誤差修正技術的井下人員MEMS定位方法［J］.傳感技術學報，2014，27(7):898－904.

［3］ 宋鏢，程磊，周明達，等.基于慣導輔助地磁的手機室內定位系統(tǒng)設計［J］.傳感技術學報，2015，28(8):1249－1254.

［4］ Groves P D.Navigation Using Inertial Sensors［J］.Aerospace and Electronic Systems Magazine，IEEE，2015，30(2):42－69.

［5］ Skog I，Handel P，Nilsson J O，et al.Zero Velocity Detection an Algorithm Evaluation［J］.Biomedical Engineering，2010，57(11): 2657－2666.

［6］ 田曉春，陳家斌，韓勇強，等.多條件約束的行人導航零速區(qū)間檢測算法［J］.中國慣性技術學報，2016，24(1):1－5.

［7］ Harle R.A Survey of Indoor Inertial Positioning Systems for Pedestrians［J］.Communications Surveys and Tutorials，IEEE，2013，15 (3):1281－1293.

［8］ Hung M L，Luan V N，Trung H D.Dynamic Human Gait Phase Detection Algorithm［C］//International Conference on Modeling of Complex Systems and Environments，2015.

［9］ Wang Z，Zhao H，Qiu S，et al.Stance Phase Detection for ZUPT-aided Foot-Mounted Pedestrian Navigation System［J］.IEEE/ ASME Transactions on Mechatronics，2015，20(6):3170－3181.

［10］ Park S K，Suh Y S.A Zero Velocity Detection Algorithm Using Inertial Sensors for Pedestrian Navigation Systems［J］.Sensors，2010，10(10):9163－9178.

［11］吳哲君，趙忠華，唐雷.基于SVM的行人步態(tài)實時分類方法［J］.電子測量技術，2015，38(7):41－44.

［12］Ren M，Pan K，Liu Y，et al.A Novel Pedestrian Navigation Algorithm for a Foot Mounted Inertial Sensor Based System［J］.Sensors，2016，16(1):139－152.

［13］費程羽，蘇中，李擎.行人慣性導航零速檢測算法［J］.傳感器與微系統(tǒng)，2016，35(3):147－150.

［14］錢偉行，朱欣華，蘇巖.基于足部微慣性/地磁測量組件的個人導航方法［J］.中國慣性技術學報，2012，20(5):567－572.

［15］ Chulliat A S，Macmillan P，Alken C，et al.The US/UK World Magnetic Model for 2015－2020［R］.National Geophysical Data Center，NOAA，2014.

［16］Widodo B，Andrei V V，Gulnara R S.Web Based Information System for Modeling and Analysis of Parameters of Geomagnetic Field［J］.Procedia Computer Science，2015，59:73－82.

［17］包志軍，馬培蓀，仝建剛，等.人行走速度規(guī)律的實驗研究［J］.實驗室研究與探索，2000，6:39－42.

［18］Browning R C，Baker E A，Herron J A，et al.Effects of Obesity and Sex on the Energetic Cost and Preferred Speed of Walking［J］.Journal of Applied Physiology，2006，100(2):390－398.

［19］周志華.機器學習［M］.北京:清華大學出版社，2016.

孫 偉(1984)，男，教授，博士生導師，黑龍江蘿北縣人。2007年于哈爾濱工程大學獲得學士學位，2011年于哈爾濱工程大學獲得博士學位。長期從事慣性導航技術研究，sunwei－3775235@163.com;

丁 偉(1992－)，男，四川省巴中市人。現(xiàn)為遼寧工程技術大學測繪與地理科學學院碩士研究生。從事慣性導航與組合導航方法研究。

Pedestrian Positioning Technology with K-Means Clustering Adaptive Zero Velocity Detection*

SUN Wei*，DING Wei，YAN Huifang
(School of Geomatics，Liaoning Technical University，F(xiàn)uxin Liaoning123000，China)

The detection accuracy of Zero velocity interval is the premise to implement Kalman filtering to clear velocity error and correct position error in time.For the existing zero velocity detection scheme，there are some problems such as threshold setting and training model accuracy.This paper proposes a zero velocity interval detection method in walking gaits based on moving variance of acceleration amplitude，an adaptive K-means clustering method is used to correct the false identified states in initial detection results.A Kalman filter is constructed in zero velocity interval，which adopt the velocity information calculated by inertial system as measurements and carry out measurement update to restrict navigation error accumulation.Series experiments are carried out，experimental results show that K-means adaptive algorithm can effectively detect zero velocity interval，and the error of the obtained position calculation is less than 2%.

pedestrian navigation;K-means clustering;Kalman filter;ZUPT

U666.12

A

1004－1699(2017)02－0296－06

C:7120;7230M;7320E

10.3969/j.issn.1004－1699.2017.02.022

項目來源:國家自然科學基金項目(41304032);高等學校博士學科點專項科研基金(新教師類)項目(20132121120005);第8批中國博士后科學基金特別項目(2015T80265);遼寧省高等學校杰出青年學者成長計劃項目(LJQ2015044);對地觀測技術國家測繪地理信息局重點實驗室開放基金項目(K201401);地球空間環(huán)境與大地測量教育部重點實驗室開放基金項目(14－01－05);江西省數(shù)字國土重點實驗室開放研究基金項目(DLLJ201501);遼寧工程技術大學研究生教育創(chuàng)新計劃(YS201608)

2016－07－05 修改日期:2016－10－12