基于半監督K-Means的屬性加權聚類算法

潘 巍 周曉英 吳立鋒 王國輝

(首都師范大學信息工程學院 北京 100048)(首都師范大學北京市高可靠嵌入式系統工程研究中心 北京 100048)(首都師范大學北京市電子系統可靠性技術研究重點實驗室 北京 100048)

基于半監督K-Means的屬性加權聚類算法

潘 巍 周曉英 吳立鋒 王國輝

(首都師范大學信息工程學院 北京 100048)(首都師范大學北京市高可靠嵌入式系統工程研究中心 北京 100048)(首都師范大學北京市電子系統可靠性技術研究重點實驗室 北京 100048)

K-Means是經典的非監督聚類算法，因其速度快，穩定性高廣泛應用在各個領域。但傳統的K-Means沒有考慮無關屬性以及噪聲屬性的影響，并且不能自動尋找聚類數目K。而目前K-Means的改進算法中，也鮮有關于高維以及噪聲方面的改進。因此，結合PCA提出基于半監督的K-Means加權屬性聚類方法。首先，用PCA得到更少更有效的特征，并計算它們的分類貢獻率(即每個特征對聚類的影響因子)。其次，由半監督自適應算法得到K。最后將加權數據集以及K應用到聚類中。實驗表明，該算法具有更好的識別率和普適性。

均值 聚類 半監督 主成分分析 屬性加權

0 引 言

隨著信息技術的快速發展，信息的重要性日益提升，同時信息的冗余也不可避免的大量存在。因此，數據挖掘技術順勢成為了最受歡迎的信息處理學科[1]。

聚類分析是一種應用廣泛的無監督方法，在數據挖掘領域中占有非常重要的位置。聚類分析是1975年出現的，Hartigan[2]在他的“聚類算法”一書中詳細的介紹了這個算法。隨后，基于各種不同思想的聚類算法相繼被提出來，包括基于分區、密度、網格以及模式等各種思想。

傳統的無監督聚類分析不依賴原始數據集的類別信息，需要由聚類學習算法自動確定，因而聚類結果的精確性并不是很高。其中，K-Means算法以其速度快，穩定性高的優點廣泛應用在各個領域，包括工程、經濟、電子、地理、統計以及心理等[3]。K-Means算法思想中，聚類數目是需要用戶根據先驗知識來獲得的[4]。這種做法不僅給用戶帶來了負擔，而且由于用戶給定聚類數目的隨機性，聚類結果的準確性也會在一定程度上降低。此外，無關屬性以及噪聲屬性同樣會降低聚類結果的準確性。

在實際問題中，通常可以很容易地獲得有限的樣本先驗信息，這些知識可以調整聚類過程，從而改善無監督聚類算法的性能。

近年來，大量的K-Means改進算法被相繼提出。2015年，胡海峰[5]提出了一種基于特征間隙的檢測簇數的譜聚類算法，根據數據之間的相似度確定簇數。同年，Jothi R[6]，提出了一種使用約束遞歸的方法得到更精確的聚類中心。2015年，魏建東[7]提出了一種層次初始的聚類個數自適應的聚類算法研究。2014年，Drias H[8]提出了一種結合K-Means和K-Medoids的算法提高了聚類精度。以上算法均未有效地減少特征數量，當特征數量比較大時，聚類結果及速度會受到影響。如果能夠在聚類前進行特征降維，將會提高聚類速度。

在特征降維算法中，PCA算法可以說是其中的經典。 PCA 是根據計算原始數據集的協方差矩陣以及協方差矩陣的特征值以及特征向量，選擇累積貢獻率(CR)比較大的特征向量得到新的向量基，最終將原始數據集投影到新的向量基中。

基于以上研究，如何將K-Means算法融入到半監督理論中選取最佳的K值，以及如何結合PCA提高聚類識別的準確率是亟待解決的問題。本文將PCA引入算法，并且利用半監督自適應的思想去解決自動的選擇聚類數目K的問題。改進算法有效地克服了噪聲和無關屬性對聚類結果的影響以及不可以自動選取聚類數目K的不足，計算效率大大的提高。

1 本文提出的算法

本文提出的基于PCA以及屬性加權的半監督聚類算法僅僅依據原始樣本訓練數據就可以自適應得到聚類數目K，在聚類效果上有著良好的表現。算法可以分為3個階段。

1.1 第一階段算法描述

(1) 首先對訓練數據集進行PCA降維，得到有效的主特征；

(2) 其次，對主特征計算累積貢獻率，并根據累積貢獻率對原始數據集進行加權；

(3) 最后得到加權后的數據集。

PCA將會把那些對分類貢獻率特別低的一些無關屬性以及噪聲屬性全部剔除掉，根據CR將原始數據集進行屬性加權得到二次處理的數據集。首先，進行歸一化(xj-min)/(max-min)處理，其中min和max分別代表整個數據集的最小樣本和最大樣本，經過歸一化處理之后，整個數據集所有樣本的值都會處于0～1之間。下一步協方差矩陣以及協方差矩陣的特征值和特征向量可根據式(1)、式(2)計算得出，之后降序排列特征值，并且選出CR值大的主成分進行數據集的降維。

協方差矩陣的計算公式如下所示：

(1)

(2)

最后計算CRi和CR，以此作為計算屬性重要度的根據。這樣根據階段1就可以得到一個經過屬性加權之后的數據集。貢獻率CRi和累計貢獻率CR可以由以下的公式進行計算得到：

(3)

(4)

1.2 第二階段算法描述

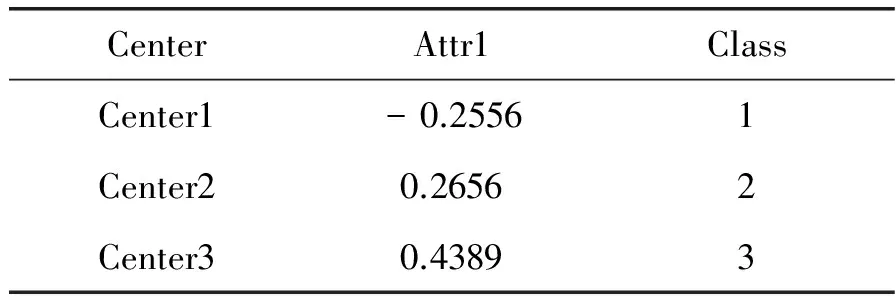
(1) 首先計算訓練數據集的聚類半徑R并且選擇初始聚類中心C1、C2；

(2) 其次，計算DBI指數，當NDBI

(3) 最后，直到當判斷結果為否時，得到聚類數目K。

第一步，根據式(5)計算得到訓練數據集的聚類半徑，式(5)如下所示：

(5)

其中，n代表訓練數據集的總體樣本數，本文定義的新的歐幾里得距離的計算式表示為：

(6)

為了考慮每一個樣本貢獻度對聚類結果的影響，在計算歐氏距離的時候，需要將分類貢獻率Ri和Rj加入到計算公式中作為一個影響因子，也就是我們在階段一所說的屬性重要度。傳統的歐氏距離沒有考慮到每個樣本屬性的不同，從而計算出的距離對于聚類不能起到很好的作用。dij表示樣本xik和xjk之間的距離，接下來就是根據距離dij選擇下一個聚類中心，下一個聚類中心的選擇由下式來決定：

d=max{min(d(c1,j),d(c2,j))}

(7)

其中，C1和C2分別表示最初的兩個聚類中心，d表示第j個樣本與聚類中心C1或者C2之間的距離。最后，DBI指數由式(8)-式(10)計算獲得。方差(所有的樣本和聚類中心之間的距離)計算式表示為：

(8)

其中，Ti、xj和Ai分別代表的是第i個聚類里面的所有的樣本數目，第i個聚類里面的第j個樣本，還有就是第i個聚類的所有樣本的平均值。第i個聚類簇與第j個聚類簇的距離矩陣Mij由下式計算得到：

(9)

(10)

其中，Si、Sj和Mij可以由式(8)、式(9)計算得到。每個樣本的最大相似度(DBI)由下式計算得到：

(11)

1.3 第三階段算法描述

(1) 將K和加權數據集作為參數傳給K-Means算法；

(2) 選擇初始聚類中心，聚類成K簇，計算平均值；并更新聚類中心；

2) 計算CEI。確定可能的化學品泄漏事故，確定ERPG-2，確定各種可能場景下的大氣泄漏量(AQ)，選擇AQ最大的場景，計算CEI，計算安全距離(HD)，匯總報告。

(3) 當不符合平方差準則函數時返回，重新選擇聚類中心；

(4) 當符合平方差準則函數時，輸出K個類簇。

屬性加權后的數據集和自適應得到的聚類數目K應用到K-Means聚類算法中，得到最終的聚類結果。

2 實驗分析

本文提出的基于PCA以及屬性加權的改進的半監督K-Means聚類算法能很好地去除掉噪聲以及無關屬性的影響，并且通過半監督算法自適應地得到聚類數目K。下面以IRIS數據集為例進行分析。

IRIS數據集共有樣本150個，特征數為5，其中屬性特征4個，分別是花萼長度、花萼寬度、花瓣長度和花瓣寬度，決策特征1個，共分3類。

2.1 屬性重要度的介紹

從圖4中可以看到屬性重要度在對分類結果的影響中發揮著極其重要的作用，不同特征屬性的分類貢獻率(CR)截然不同。通過圖4(a)效果圖展示，我們可以看到，花萼長度和花萼寬度這兩個特征屬性的分類結果非常不明顯。如果我們應用這兩個屬性來作為聚類的主要屬性，那么會出現很大的錯誤。圖4(b)和(c)中，通過花萼長度和花瓣長度以及花萼寬度和花瓣寬度的組合來進行聚類，界限模糊的現象大大的改善了，圖4(d)是通過花瓣長度以及花瓣寬度來進行聚類，可以看到展示的分類效果最好，兩類數據很好地區別開來，聚類簇之間的界限比較明顯，并且聚類簇內部非常緊湊。因此應該給予花瓣長度和花瓣比其他特征屬性更高的屬性重要度。

圖4 IRIS不同屬性分類結果

如圖5所示，IRIS數據集中每個特征的屬性重要度都是不同的，其中，花瓣長度的屬性重要性最高。

圖5 IRIS分類貢獻率

從表1中可以看到，IRIS數據集的主特征花瓣長度屬性的累積分類貢獻率已經達到97%，遠遠超過其他特征屬性的累積分類貢獻率。也就是說，花瓣長度這個特征屬性可以很好地還原原始數據集IRIS，因此選擇這個屬性作為主屬性。

表1 IRIS分類累積貢獻率

如表2所示，Center代表初始得到的聚類中心，Attr代表初始聚類中心的每一個特征屬性。

表2 IRIS數據集中初始的三個聚類中心

表2中，由于開始進行了主特征屬性的篩選，因此只留下花瓣長度一個主特征，根據累積貢獻率選取的初始三個聚類中心分別來自三個不同類，這樣聚類出的結果相對來說會更加準確。

圖6表示的是IRIS數據集在兩個特征屬性在傳統的K-Means的分類效果圖在處理前后的對比圖，(a)是原始的分類效果圖，其中位于右下角的兩類有大面積的混合；(b)中，三類很好地分了開來，并且達到了類間距離很大、類內距離很小的標準聚類準則。

圖6 IRIS分類對比

2.2 本文改進算法有效性驗證

本文采用半監督的方式加強K值的準確性。下面用IRIS數據集以及Wine數據集與其他改進K-Means算法進行比較。K-Means算法表示的是原始算法，PCA-K-Means指的是經過本文算法進行改進后的算法，SC-ICNE表示的是文獻[5]中基于特征間隙改進的譜聚類算法，IV-AFS表示的是文獻[6]中融合免疫接種機制的改進魚群聚類算法，DHIKM表示的是文獻[7]中基于層次的聚類個數自適應改進聚類算法，FO-CA指的是文獻[8]中基于距離差異度組合權重的多屬性數據分類方法，如表3所示。

表3 算法比較

從表3中可以看到，本文方法在IRIS數據集中表現最好，在Wine數據集中表現也不錯，僅略次于FO-CA算法，本文算法總體識別率最高。

2.3 本文改進算法的普適性驗證

本文為了更加準確清晰地描述該改進算法的有效性，分別選取了離散數據集以及連續數據集各8個數據集來進行效果的驗證。

表4介紹的是離散數據集的具體信息，Samples表示每一個數據集的樣本總數，Attr表示的每一個數據集的特征總數，Class表示的是每一個數據集的類別總數，Percent表示的每一個數據集的每一個類別在整個數據集中的所占百分比。

表4 離散數據集介紹

表5主要介紹了每一個連續數據集的情況。

表5 連續數據集的介紹

本文所選擇的數據集，不論是離散數據集還是連續數據集，都力求做到多樣性，在樣本個數、特征個數以及類別數上都各不相同，以此來驗證本文改進算法的普適性。

2.4 自適應得到K值

驗證半監督自適應得到K值的有效性，選取的數據集同時包括離散數據集以及連續數據集，并且在樣本數、特征數目以及類別數上有一定差別的數據集來說明改進算法的有效性。

從表6中可以看到，當訓練數據集占得百分比逐漸增多的時候，自適應得到的聚類數目K也越來越準確。如表7和表8所示，不論是在連續數據集還是離散數據集的聚類識別率上，本文提出的SP-Kmeans算法都有較好的表現。

表6 聚類數目

注：數據集后面的括號中代表的是數據集本身的類別數，百分比指的是訓練數據集占原數據集的比例

表7 離散數據集識別率的比較

續表7

注：括號中數字代表同樣一個離散數據集各個算法的分類識別率，本文的PCA-K-Means改進算法的排名總體最高，均為前2名，即使第2名也遠遠高于其他算法的性能

表8 連續數據集識別率的比較

注：括號中數字代表同樣一個離散數據集各個算法的分類識別率，本文提出的PCA-K-Means改進算法在8個連續數據集中，有7個排名第一，1個第二，但也均遠遠高于其他算法的識別率

圖7為表7的圖形化表示，X軸表示8個離散數據集，Y軸表示每一種方法在此數據集上的分類識別率。可以直觀看到，本文改進算法在選擇的離散數據集中表現良好，聚類識別率高于其他聚類算法。

圖7 離散數據集的實驗結果的折線圖

圖8為表8的圖形化表示，X軸表示8個連續數據集，Y軸同樣表示每一種方法在此數據集上的分類識別率。從圖中可以看到，其他五種聚類算法識別率非常不穩定，且識別率準確性不是很好。隨著數據集類別數目的變化，分類識別率有大幅度升降，而本文提出的改進算法不論數據集類別數目如何變化，分類識別率始終保持在一定范圍之內，穩定性比較高。

對比圖7和圖8，可以看到本文方法對于連續型數據集有著較好的分類識別率，而對于離散型數據集則沒有達到連續型數據集那樣好的效果，但還是高于其他的聚類算法。

圖8 連續數據集的實驗結果的折線圖

3 結 語

本文提出了一種基于半監督的PCA屬性加權的K-means聚類算法，通過提出的屬性重要度以及特征屬性的聚類貢獻率等影響因子的概念，不僅有效地去除了無關屬性以及噪聲屬性對聚類結果精確度的影響，并且通過自適應算法自動得到聚類數目K,減輕了用戶的負擔。通過在UCI公開數據集上對比文獻中提到的改進算法的對比實驗，驗證了本文改進算法的有效性和精確性。

[1]HamrouniT,SlimaniS,CharradaFB.Adataminingcorrelatedpatterns-basedperiodicdecentralizedreplicationstrategyfordatagrids[J].JournalofSystemsandSoftware,2015,110:10-27.

[2] 周世兵,徐振源,唐旭清.基于近鄰傳播算法的最佳聚類數確定方法比較研究[J].計算機科學,2011,38(2):225-228.

[3]LiC,ZhangY,JiaoM,etal.Mux-Kmeans:multiplexkmeansforclusteringlarge-scaledataset[C]//Proceedingsofthe5thACMworkshoponScientificcloudcomputing.ACM,2014:25-32.

[4] 樊寧.K均值聚類算法在銀行客戶細分中的研究[J].計算機仿真,2011,28(3):369-372.

[5] 胡海峰,劉萍萍.一種基于特征間隙的檢測簇數的譜聚類算法[J].計算機技術與發展,2015,25(9):37-42.

[6]JothiR,MohantySK,OjhaA.OnCarefulSelectionofInitialCentersforK-meansAlgorithm[C]//Proceedingsof3rdInternationalConferenceonAdvancedComputing,NetworkingandInformatics.SpringerIndia,2016.

[7] 魏建東,陸建峰,彭甫镕.一種層次初始的聚類個數自適應的聚類方法研究[J].電子設計工程,2015(6):5-8.

[8]DriasH,CherifNF,KechidA.k-MM:AHybridClusteringAlgorithmBasedonk-Meansandk-Medoids[M]//AdvancesinNatureandBiologicallyInspiredComputing.SpringerInternationalPublishing,2016.

ATTRIBUTE-WEIGHTED CLUSTERING ALGORITHM BASED ONSEMI-SUPERVISED K-MEANS

Pan Wei Zhou Xiaoying Wu Lifeng Wang Guohui

(CollegeofInformationEngineering,CapitalNormalUniversity,Beijing100048,China)(BeijingEngineeringResearchCenterofHighReliableEmbeddedSystem,CapitalNormalUniversity,Beijing100048,China)(BeijingKeyLaboratoryofElectronicSystemReliableTechnology,CapitalNormalUniversity,Beijing100048,China)

K-Means is a classic unsupervised clustering algorithm which is widely applied in various fields for its high speed and high stability. However, the traditional K-Means methods do not take unrelated attributes and the impact of noise into consideration. They also cannot automatically look for the number of clusters K.Atpresent,theimprovedK-Meansalgorithmsalsorarelyfocusonhigh-dimensionaldataandnoiseattributes.Therefore,thispaperproposesanattribute-weightedclusteringalgorithmbasedonsemi-supervisedK-MeansassociatedwithPCA.Firstly,thedimensionreductionisachievedbyintroducingPCA,andthecontributionrateofeachdimensionclassificationcharacteristics(theimpactfactorofclusteringprocessedbyeachfeatureattribute)iscalculated.Secondly,thenumberofclustersKisobtainedthroughanadaptivesemi-supervisedalgorithm.Finally,theweighteddatasetsandKareappliedtoclustering.Experimentalresultsshowthattheproposedmethodhasbetterrecognitionrateanduniversality.

Means Clustering Semi-supervised Principal Component Analysis Attribute-weighted

2016-03-02。國家自然科學

61202027)；北京市屬高等學校創新團隊建設與教師職業發展計劃項目(IDHT20150507)。潘巍，副教授，主研領域：信息融合與模式識別。周曉英，碩士生。吳立鋒，副教授。王國輝，講師。

TP

ADOI:10.3969/j.issn.1000-386x.2017.03.034