基于信任度的虛擬企業(yè)盟主伙伴雙向選擇模型

林 楊 黎元生 王應(yīng)明

1(福建師范大學(xué)經(jīng)濟(jì)學(xué)院 福建 福州 350117)2(福州大學(xué)決策科學(xué)研究所 福建 福州 350116)

基于信任度的虛擬企業(yè)盟主伙伴雙向選擇模型

林 楊1,2黎元生1王應(yīng)明2

1(福建師范大學(xué)經(jīng)濟(jì)學(xué)院 福建 福州 350117)2(福州大學(xué)決策科學(xué)研究所 福建 福州 350116)

選擇值得信任且有競爭力的合作伙伴對(duì)于組建虛擬企業(yè)至關(guān)重要。針對(duì)以往虛擬企業(yè)伙伴選擇僅從盟主方的角度對(duì)備選伙伴進(jìn)行單向評(píng)價(jià)和選擇，而沒有從盟主與伙伴雙方互評(píng)互選的角度考慮，導(dǎo)致組建的虛擬企業(yè)穩(wěn)定性較差，提出一種基于信任度的盟主與伙伴企業(yè)雙向選擇模型。先定義信任關(guān)系矩陣的概念，并通過最大化信任關(guān)系矩陣各列向量與其排序向量的關(guān)聯(lián)測(cè)度，得到最優(yōu)排序向量并將其作為信任度信息，然后，建立一種基于雙方信任度的雙向選擇優(yōu)化模型，并求解得到結(jié)果。最后，通過實(shí)例分析說明所提方法的可行性和合理性。

虛擬企業(yè) 信任關(guān)系矩陣 信任度 排序向量 關(guān)聯(lián)測(cè)度 雙向選擇模型

0 引 言

隨著市場(chǎng)環(huán)境日趨復(fù)雜多變，降低運(yùn)營成本，塑造企業(yè)快速反應(yīng)能力成為現(xiàn)代企業(yè)管理的重要內(nèi)容。虛擬企業(yè)VE(virtual enterprise)作為一種能對(duì)企業(yè)外部資源進(jìn)行優(yōu)化整合，敏捷響應(yīng)市場(chǎng)需求的有效途徑[1]，已成為眾多企業(yè)(特別是制造業(yè))的現(xiàn)實(shí)選擇。“虛擬企業(yè)”一詞源于1991年美國R. Nagel、K.Preiss和S.Goldman三位學(xué)者對(duì)于基礎(chǔ)敏捷制造模式的研究[2-3]；但至今學(xué)術(shù)界對(duì)VE還未形成統(tǒng)一的定義。一般認(rèn)為，VE是一種新型的企業(yè)組織運(yùn)營模式，由兩個(gè)或多個(gè)自治的、多樣的且地理分散的公司以契約(協(xié)議)為紐帶，組建成的可快速反應(yīng)市場(chǎng)機(jī)遇的臨時(shí)聯(lián)盟[4]。

如何選擇有競爭力、敏捷的且相匹配的合作伙伴對(duì)于盟主企業(yè)組建VE至關(guān)重要，也是VE正常生產(chǎn)、運(yùn)作的重要保證[5-6]。學(xué)術(shù)界對(duì)VE的伙伴選擇問題進(jìn)行了大量研究。一些學(xué)者從多屬性決策的角度，結(jié)合層次分析法(AHP)研究該問題：徐澤水[7]研究了屬性及偏好信息均為三角模糊數(shù)的VE伙伴選擇問題；對(duì)權(quán)重信息未知或不完全的情形，給出了一種基于期望值的模糊多屬性決策方法；Meade等[8]提出基于層次分析法(AHP)的伙伴選擇與管理機(jī)制，從定性定量兩方面進(jìn)行分析；蔚麗峰等[9]運(yùn)用模糊數(shù)據(jù)挖掘?qū)锇槠髽I(yè)進(jìn)行聚類分析，然后使用AHP法得到候選企業(yè)的優(yōu)先順序；盧紀(jì)華等[10]利用DEA和AHP法對(duì)合作伙伴進(jìn)行分類，并對(duì)同一類伙伴企業(yè)進(jìn)行評(píng)價(jià)選擇；但是，基于AHP的伙伴企業(yè)選擇較依賴決策者的主觀經(jīng)驗(yàn)，得到結(jié)果的主觀性較大。為克服AHP法的不足，一些學(xué)者嘗試采用逼近理性點(diǎn)法(TOPSIS)進(jìn)行研究。劉帥華等[11]建立伙伴企業(yè)的指標(biāo)體系并對(duì)各指標(biāo)組合賦權(quán)，提出一種綜合TOPSIS、熵值法與AHP的決策模型；Fei等[4]研究了評(píng)價(jià)信息為不完全區(qū)間值，且分別包含偏差度和風(fēng)險(xiǎn)因子兩種情況；并給出基于 TOPSIS的群決策方法；此外，近年來也有學(xué)者將信任機(jī)制引入到VE伙伴選擇研究，如田俊鋒等[12]結(jié)合信譽(yù)和基于信任的合作機(jī)制，提出信任場(chǎng)的概念并建立信任場(chǎng)理論模型；并分析了基于信任場(chǎng)模型的VE伙伴選擇方法；還有一些學(xué)者嘗試使用啟發(fā)式算法解決該問題：Ip等[13]研究滿足交貨期約束和生產(chǎn)成本最小化為目標(biāo)的伙伴選擇模型，設(shè)計(jì)了一種基于規(guī)則的遺傳算法；賈瑞玉等[14]給出一個(gè)基于粗糙集和自適應(yīng)遺傳算法的決策模型，允許先驗(yàn)知識(shí)未知下計(jì)算屬性權(quán)重再進(jìn)行選擇；需指出的是，啟發(fā)式搜索算法往往過程復(fù)雜，計(jì)算量大且易陷入局部最優(yōu)[15]。

現(xiàn)有VE伙伴選擇方法大多僅站在盟主方的角度，對(duì)候選伙伴企業(yè)進(jìn)行單向評(píng)價(jià)排序、擇優(yōu)；現(xiàn)實(shí)市場(chǎng)環(huán)境中，雖然在形式上伙伴企業(yè)對(duì)盟主企業(yè)表現(xiàn)出一定依賴性，但本質(zhì)上雙方均是獨(dú)立存在的企業(yè)實(shí)體，都具有一定的選擇權(quán)和被選擇權(quán)；另一方面，VE是各方企業(yè)建立在信任基礎(chǔ)上的一種動(dòng)態(tài)聯(lián)盟，各方之間的相互信任是組建VE的靈魂[12]，而合作伙伴的選擇又是基于信任而做出的決策行為。所以，若僅僅對(duì)伙伴企業(yè)單方進(jìn)行評(píng)價(jià)，缺乏從盟主與伙伴雙方互相選擇、互相決策的層面動(dòng)態(tài)考慮該問題，就不能完整地描述雙方的主觀(選擇)傾向，不利于組建穩(wěn)定的VE。為此，本文考慮多個(gè)盟主與多個(gè)伙伴企業(yè)共存情形下，組建VE盟主與伙伴雙方的雙向選擇問題。借鑒AHP[16]中判斷矩陣的定義，本文提出了信任關(guān)系矩陣和信任度的概念；并運(yùn)用匹配決策理論[17]分析該問題。

1 信任關(guān)系矩陣及排序向量

1.1 相關(guān)定義和問題描述

AHP法是一種定性和定量相結(jié)合的決策方法[18],用于解決很難或無法直接給出所有方案排序結(jié)果的決策問題。AHP法的關(guān)鍵是如何形成判斷矩陣并計(jì)算屬性權(quán)重。受到判斷矩陣通過兩兩比較全體對(duì)象得到各對(duì)象偏好值的啟發(fā),本文定義了信任關(guān)系矩陣TRM(trust relationship matrix)；依據(jù)判斷矩陣的思想,在形成VE的“盟主—伙伴”雙方候選企業(yè)中,各方通過兩兩比較對(duì)方所有企業(yè),給出矩陣形式的對(duì)比值,形成TRM。TRM中的元素值是決策方(盟主/伙伴企業(yè))關(guān)于對(duì)方所有候選企業(yè),在給定評(píng)價(jià)指標(biāo)框架下兩兩比較后給出的一種信任程度；它反映了決策方對(duì)于候選企業(yè)能否按照預(yù)期完成某種任務(wù)的期望。值得一提的是,對(duì)VE的評(píng)價(jià)指標(biāo)選取以及指標(biāo)體系的建立已有相關(guān)文獻(xiàn),本文不討論指標(biāo)的選取過程。

定義1[19]矩陣P=(pij)n×n,其中pij>0；若pii=0.5pij+pji=1,?i, j=1, 2,…,n, i ≠ j, 則P為信任關(guān)系矩陣。稱P滿足一致性,若有pikpkjpji=pkipjkpij,i,j,k=1,2,…,n。

(1)

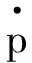
(2)

k=1, 2,…,n

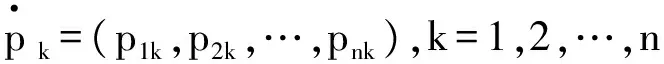
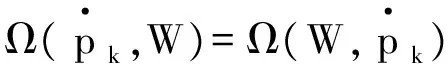
不難驗(yàn)證推論①、②；為證明推論③,將式(1)代入式(2)，即：

(3)

k=1,2,…,n

化簡得Ωk=1,k=1,2,…,n；故推論③成立。

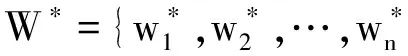
1.2 確定TRM的排序向量

(4)

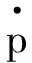
(5)

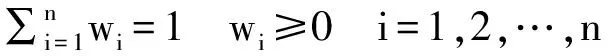
(6)

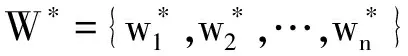
(7)

(8)

(9)

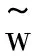
(10)

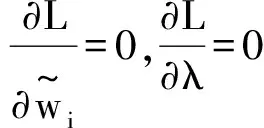
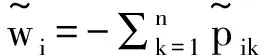
(11)

(12)

化簡得：

(13)

式(13)代入式(11),得：

(14)

證畢。

證明 根據(jù)式(7)知：

(15)

又P滿足一致性,所以Ωk=1,k=1,2,…,n；則：

(16)

由推論1知：

代入式(16)得：

所以：

(17)

證畢。

2 基于信任度的雙向選擇模型

2.1 雙向選擇模型的建立

(18a)

(18b)

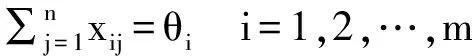
(18c)

(18d)

xij∈{0,1}i=1, 2,…,m,j=1, 2,…,n

(18e)

其中,目標(biāo)函數(shù)(18a)為最大化所有盟主企業(yè)對(duì)所有伙伴企業(yè)的信任度；(18b)為最大化所有伙伴企業(yè)對(duì)所有盟主企業(yè)的信任度；雙方的信任度越大,則相互選中的“盟主—伙伴”所組建成VE的穩(wěn)定性也越高；約束條件(18c)表示Ai至多選擇θi個(gè)伙伴企業(yè)；約束條件(18d)表示Bj至多與某一個(gè)盟主企業(yè)組建VE。

2.2 雙向選擇模型的求解

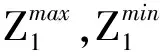
(19)

進(jìn)而引入權(quán)重變量ω1和ω2,其中0≤ω1,ω2≤1,ω1+ω2=1；分別表示αz1與αz2在單目標(biāo)函數(shù)中所占的比重；則轉(zhuǎn)化后的單目標(biāo)優(yōu)化模型(Ⅲ)為：

MinZ=ω1αz1+ω2αz2

(20a)

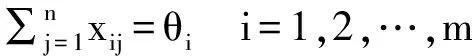
(20b)

(20c)

xij∈{0, 1}i=1,2,…,mj=1,2,…,n

(20d)

其中,權(quán)重ω1和ω2描述了盟主企業(yè),以及伙伴企業(yè)在雙向選擇中的重要程度,一般ω1≥ω2；若參與組建虛擬企業(yè)的雙方具有平等性,則ω1=ω2=0.5。可以看出,模型(III)的目標(biāo)函數(shù)以及約束條件均為線性，另外,考慮到參與組建VE的盟主和伙伴企業(yè)的個(gè)數(shù)一般不多,即所求解的問題規(guī)模不大；所以可采用線性規(guī)劃方法求解；或使用優(yōu)化軟件包,例如Matlab2009,Lingo11等求解。

綜上所述,可將基于信任度的虛擬企業(yè)盟主與伙伴雙向選擇模型的具體步驟歸納如下：

Step1 識(shí)別盟主方和伙伴方企業(yè),并得到雙方給出的信任關(guān)系矩陣(TRM)；

Step2 依據(jù)推論1、推論2計(jì)算各TRM的最優(yōu)排序向量；

Step3 將求出的最優(yōu)排序向量作為雙方參與雙向選擇的信任度；

Step4 建立基于信任度的VE盟主伙伴雙向選擇模型(Ⅱ)；

Step5 依據(jù)式(19)-式(20),將模型(Ⅱ)轉(zhuǎn)化為單目標(biāo)優(yōu)化模型(III)并求解；

Step6 根據(jù)得到的最優(yōu)解,盟主和伙伴雙方企業(yè)進(jìn)行雙向選擇。

3 算 例

中航工業(yè)下屬兩家航空設(shè)備制造企業(yè)(盟主方：A1、A2)要完成一批項(xiàng)目，由于不完全具備完成項(xiàng)目的所有資源，需聯(lián)合一些具有互補(bǔ)資源的伙伴企業(yè)共同組建虛擬企業(yè). 盟主企業(yè)A1、A2的項(xiàng)目共分為鍛造、軋制、焊接、切削和檢驗(yàn)五個(gè)階段；其中，企業(yè)A1在軋制、切削2個(gè)階段，A2在焊接、切削2個(gè)階段均需要1名合作伙伴；經(jīng)過初選，存在6個(gè)候選伙伴企業(yè)(伙伴方：B1～B6), 假定每個(gè)候選企業(yè)至多與一個(gè)盟主企業(yè)共同組建；另外,對(duì)盟主方A1、A2而言，因不同階段的伙伴企業(yè)可同時(shí)進(jìn)行評(píng)價(jià)選擇；可將A1參與雙向選擇的軋制、切削兩個(gè)階段分別記為A11、A12；同理，將A2的焊接、切削兩個(gè)階段記為A21、A22。雙方各負(fù)責(zé)人和有關(guān)專家依據(jù)文獻(xiàn)[7]建議的指標(biāo)，對(duì)對(duì)方所有對(duì)象進(jìn)行評(píng)價(jià)并給出相應(yīng)的TRM如下：

采用本文提出的VE“盟主—伙伴”企業(yè)雙向選擇方法，根據(jù)1.2節(jié)的推論1，得到盟主和伙伴雙方TRM的排序向量，如表1、表2所示。

表1 盟主方TRM的排序向量

表2 伙伴方TRM的排序向量

然后，將求得的盟主—伙伴雙方的TRM排序向量作為參與雙向選擇的信任度；并在信任度矩陣基礎(chǔ)上，建立2.1節(jié)所闡述的雙向選擇模型：

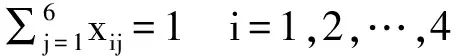
xij∈{0, 1} i=1,2,…,4 j=1,2,…,6

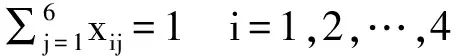
xij∈{0, 1}i=1,2,…,4j=1,2,…,6

再求解上述模型, 得到的最優(yōu)解為：

即盟主企業(yè)A1在軋制階段的最優(yōu)伙伴為B4，在切削階段的最優(yōu)伙伴為B2；盟主企業(yè)A2在焊接階段的最優(yōu)伙伴為B6，切削階段最優(yōu)伙伴為B5。

4 結(jié) 語

合作伙伴的選擇在組建VE過程中是一個(gè)十分關(guān)鍵且復(fù)雜的環(huán)節(jié)。是否選擇相互信任、有競爭力的合作伙伴關(guān)系到VE的績效與成敗。然而,現(xiàn)有VE伙伴選擇方法只站在盟主企業(yè)的立場(chǎng)對(duì)候選伙伴進(jìn)行評(píng)價(jià)、擇優(yōu)；忽略了雙方的對(duì)等性,沒有從伙伴企業(yè)的角度對(duì)盟主方企業(yè)進(jìn)行評(píng)價(jià)；從而割裂了雙方作為獨(dú)立實(shí)體之間存在的相互聯(lián)系與作用。因此,本文提出一種基于信任度的VE盟主與伙伴的雙向選擇模型,彌補(bǔ)已有研究的不足。通過最大化雙方給出的信任關(guān)系矩陣與其對(duì)應(yīng)排序向量的關(guān)聯(lián)測(cè)度,求得信任關(guān)系矩陣的最優(yōu)排序向量并將其作為信任度；在此基礎(chǔ)上建立雙向選擇模型,并轉(zhuǎn)化為單目標(biāo)求解得到最終結(jié)果。本文提出的方法具有較好的數(shù)學(xué)基礎(chǔ),且具有概念清晰、計(jì)算量小等特點(diǎn)；為解決實(shí)際的VE伙伴選擇問題提供了一種新的途徑。

[1] 馮蔚東.虛擬企業(yè)中的風(fēng)險(xiǎn)管理與控制研究[J].管理科學(xué)學(xué)報(bào),2001,4(3):1-8.

[2]GoldmanSL,NagelRN,PreissK,etal.Agilecompetitorsandvirtualorganizations[M].NewYork:VanNostrandReinhold,1995.

[3] 呂衛(wèi)華.虛擬企業(yè)研究回顧與展望[J].科學(xué)管理研究,2014,5:88-91.

[4]YeF,LiYN.Groupmulti-attributedecisionmodeltopartnerselectionintheformationofvirtualenterpriseunderincompleteinformation[J].ExpertSystemswithApplications,2009,36(5):9350-9357.

[5]MartinezMT,FouletierP,ParkKH,etal.Virtualenterprise-organisation,evolutionandcontrol[J].Internationaljournalofproductioneconomics,2001,74(1):225-238.

[6]MikhailovL.Fuzzyanalyticalapproachtopartnershipselectioninformationofvirtualenterprises[J].Omega,2002,30(5):393-401.

[7] 徐澤水.基于期望值的模糊多屬性決策法及其應(yīng)用[J].系統(tǒng)工程理論與實(shí)踐,2004,24(1):109-113.

[8]MeadeLM,LilesDH,SarkisJ.Justifyingstrategicalliancesandpartnering:aprerequisiteforvirtualenterprising[J].Omega,1997,25(1):29-42.

[9] 蔚麗峰,高虎明.基于模糊數(shù)據(jù)挖掘和AHP的虛擬企業(yè)伙伴選擇研究[J].科技通報(bào),2012,28(6):141-143.

[10] 盧紀(jì)華,李艷.基于DEA/AHP的虛擬企業(yè)合作伙伴選擇研究[J].東北大學(xué)學(xué)報(bào)(自然科學(xué)版),2008,29(11):1661-1664.

[11] 劉帥華,郭堯琦.基于AHP和熵的TOPSIS方法的虛擬企業(yè)合作伙伴選擇[J].湖南理工學(xué)院學(xué)報(bào),2008,21(3):16-18.

[12] 田俊峰,王閆杰.虛擬企業(yè)伙伴選擇的信任場(chǎng)模型[J].系統(tǒng)工程理論與實(shí)踐,2014,12:244-253.

[13]IpWH,HuangM,YungKL,etal.Geneticalgorithmsolutionforarisk-basedpartnerselectionprobleminavirtualenterprise[J].Computers&OperationsResearch,2003,30(2):213-231.

[14] 賈瑞玉,潘雯雯,劉范范.粗糙集與遺傳算法的虛擬企業(yè)伙伴選擇[J].哈爾濱工程大學(xué)學(xué)報(bào),2012,33(6):730-734.

[15] 郭觀七,喻壽益,賀素良.自適應(yīng)小生態(tài)遺傳算法的理論分析和加速技術(shù)[J].計(jì)算機(jī)學(xué)報(bào),2003,26(6):753-758.

[16]SattyTL.Theanalytichierarchyprocess[M].McGraw-HillPress,NewYork,1980.

[17]EcheniqueF.Whatmatchingscanbestable?Thetestableimplicationsofmatchingtheory[J].MathematicsofOperationsResearch,2008,33(3):757-768.

[18]SaatyTL.Decision-makingwiththeAHP:Whyistheprincipaleigenvectornecessary[J].Europeanjournalofoperationalresearch,2003,145(1):85-91.

[19]XuZ,DaQ.Aleastdeviationmethodtoobtainapriorityvectorofafuzzypreferencerelation[J].EuropeanJournalofOperationalResearch,2005,164(1):206-216.

[20]WangYM,FanZP.Groupdecisionanalysisbasedonfuzzypreferencerelations:logarithmicandgeometricleastsquaresmethods[J].AppliedMathematicsandComputation,2007,194(1):108-119.

[21]HamersL,HemeryckY,HerweyersG,etal.Similaritymeasuresinscientometricresearch:theJaccardindexversusSalton’scosineformula[J].InformationProcessing&Management,1989,25(3):315-318.

[22] 江文奇.一種判斷矩陣的不一致性調(diào)整方法[J].系統(tǒng)工程與電子技術(shù),2009,31(9):2129-2132.

[23] 樊治平,樂琦.基于完全偏好序信息的嚴(yán)格雙邊匹配方法[J].管理科學(xué)學(xué)報(bào),2014,17(1):21-34.

[24]CohonJL.Multi-objectiveprogrammingandplanning[M].MathematicsinScienceandEngineering,NewYork:AcademicPress,1978.

[25]ChenJ,ZhangZM,TianXT,etal.Anapproachtopartnerselectioninvirtualenterprisesbasedongreyrelationalanalysis[J].JournalofEngineeringManufacture,2011,225(1):2292-2301.

[26] 張巍,朱艷春,孫寶文.基于信任的虛擬企業(yè)伙伴選擇模型構(gòu)建及仿真[J].計(jì)算機(jī)集成制造系統(tǒng),2015,21(2):528-536.

MUTUAL SELECTION MODEL FOR LEADER AND PARTNER IN VIRTUALENTERPRISES BASED ON TRUST DEGREE

Lin Yang1,2Li Yuansheng1Wang Yingming2

1(SchoolofEconomics,FujianNormalUniversity,Fuzhou350117,Fujian,China)2(InstituteofDecisionScience,FuzhouUniversity,Fuzhou350116,Fujian,China)

It’s crucial to choose trustworthy and competitive partners in the formation of VE (virtual enterprise). Aiming at the situation that only unidirectional evaluation is made by leaders to choose alternative partners rather than mutual evaluation and selection are made between leaders and partners, which leads to a relatively weak stability while forming a VE, a mutual selection model based on trust degree is proposed. Firstly, the concept of TRM (trust relationship matrix) is defined. Through maximizing the correlation measure between each column of TRM and its ordering vector, the optimal ordering vector can be generated as the trust degree in next process. Then, based on the trust degree of both leaders and partners, an optimal model is built so that results can be obtained. Finally, the feasibility and rationality of the proposed method are proved through a practical case.

Virtual enterprise Trust relationship matrix Trust degree Ordering vector Correlation measure Mutual selection model

2016-02-23。國家自然科學(xué)

71371053)；福建省社科規(guī)劃青年項(xiàng)目(FJ2015C111)；福建師大本科教學(xué)改革研究項(xiàng)目(I201501002)。林楊，講師，主研領(lǐng)域：最優(yōu)化理論。黎元生，教授。王應(yīng)明，教授。

TP391

A

10.3969/j.issn.1000-386x.2017.03.036