基于棧式自編碼器模型的匯率時間序列預測

寇茜茜 何希平,2,3*

1(重慶工商大學電子商務與供應鏈系統(tǒng)重慶市重點實驗室 重慶 400067)2(重慶市工商大學計算機科學與信息工程學院 重慶 400067)3(重慶工商大學重慶市檢測控制集成系統(tǒng)工程實驗室 重慶 400067)

基于棧式自編碼器模型的匯率時間序列預測

寇茜茜1何希平1,2,3*

1(重慶工商大學電子商務與供應鏈系統(tǒng)重慶市重點實驗室 重慶 400067)2(重慶市工商大學計算機科學與信息工程學院 重慶 400067)3(重慶工商大學重慶市檢測控制集成系統(tǒng)工程實驗室 重慶 400067)

針對目前具有非線性特征的金融時間序列淺層模型預測精度有限的問題，提出一種由底層的棧式自編碼器和頂層的回歸神經(jīng)元組成的棧式自編碼神經(jīng)網(wǎng)絡預測模型。首先利用自編碼器的無監(jiān)督學習機制對時間序列進行特征識別與學習，逐層貪婪學習神經(jīng)網(wǎng)絡各層，之后將棧式自編碼器擴展為有監(jiān)督機制的SAEP模型，將SAE學習到的參數(shù)用于初始化神經(jīng)網(wǎng)絡，最后利用有監(jiān)督學習對權值進行微調。實驗設計利用匯率時間序列作為訓練及測試樣本，與目前較成熟的方法進行對比實驗，驗證了所提出的模型在匯率時序預測應用中的有效性。

時間序列 預測 深度學習 棧式自編碼器 特征學習 深度神經(jīng)網(wǎng)絡

0 引 言

基于時間序列分析的特征識別與預測已經(jīng)成為國內外研究的熱點，而構造有效的數(shù)據(jù)分析模型是精準預測的關鍵步驟[1]。對于現(xiàn)在普遍存在的時間序列來說，傳統(tǒng)的淺層模型已經(jīng)不能有效表達其深層次的特征[2]。為更好地模擬應用中的時間序列，目前通用的做法是設計特征選擇器，但對于每項任務來說，設計特征選擇器需要專家經(jīng)驗且耗時；另一種做法是從無類別標簽的數(shù)據(jù)中采取無監(jiān)督學習機制學習特征[3-4]，這一做法的優(yōu)勢在于無需設計特征選擇器即可自動學習序列數(shù)據(jù)之間潛在的關聯(lián)關系。深度神經(jīng)網(wǎng)絡產(chǎn)生于人工智能研究背景，并且已經(jīng)在多個時間序列應用領域取得較好的結果，例如語音識別[5]、運動肢體識別[6]、視頻目標分類[7]等。匯率時間序列具有動態(tài)性和不確定性，含有大量噪音干擾，通常呈現(xiàn)出非線性特征，對于匯率時序的預測一直是國內外金融研究中重要且具有挑戰(zhàn)的工作之一[8]，目前對于匯率的時序預測模型有計量模型，例如ARIMA模型[9]、ARCH模型[10]、GARCH模型[11]，這些模型的改進及組合都在一定程度上推進了匯率預測的研究；另一類為基于機器學習的模型，例如人工神經(jīng)網(wǎng)絡(ANN)[11-13]和支持向量機(SVM)[14]。現(xiàn)有的模型預測精度受限問題主要集中在淺層學習難以挖掘時間序列的深層次特征。針對匯率預測精度受限的問題，本文提出一種由底層的棧式自編碼器和頂層的回歸層組成的深度學習預測模型，同時該模型的提出，尤其是無監(jiān)督學習機制，為時間序列的實時性預測提供了一種新的思路和方向。

基于以上的分析，本文研究棧式自編碼預測模型SAEP(Stacked AutoEncoder based Prediction model)及其匯率時序預測應用。首先，利用無監(jiān)督逐層貪婪學習的自編碼器，堆疊實現(xiàn)對深度神經(jīng)網(wǎng)絡的預訓練，之后再用監(jiān)督學習對網(wǎng)絡參數(shù)進行微調，然后借助學習到的網(wǎng)絡模型實現(xiàn)時間序列的預測。該模型尤其可以解決具有非線性特征的時間序列預測精度受限的問題。

1 棧式自編碼器與預測模型

1.1 自編碼器

自編碼器AE(AutoEncoder)是嘗試學習一個恒等函數(shù)，使得輸出值等于輸入值，現(xiàn)假設有一個時間序列樣本{y(1),y(2),…,y(n)}，對于t時刻的自編碼結構如圖1所示。

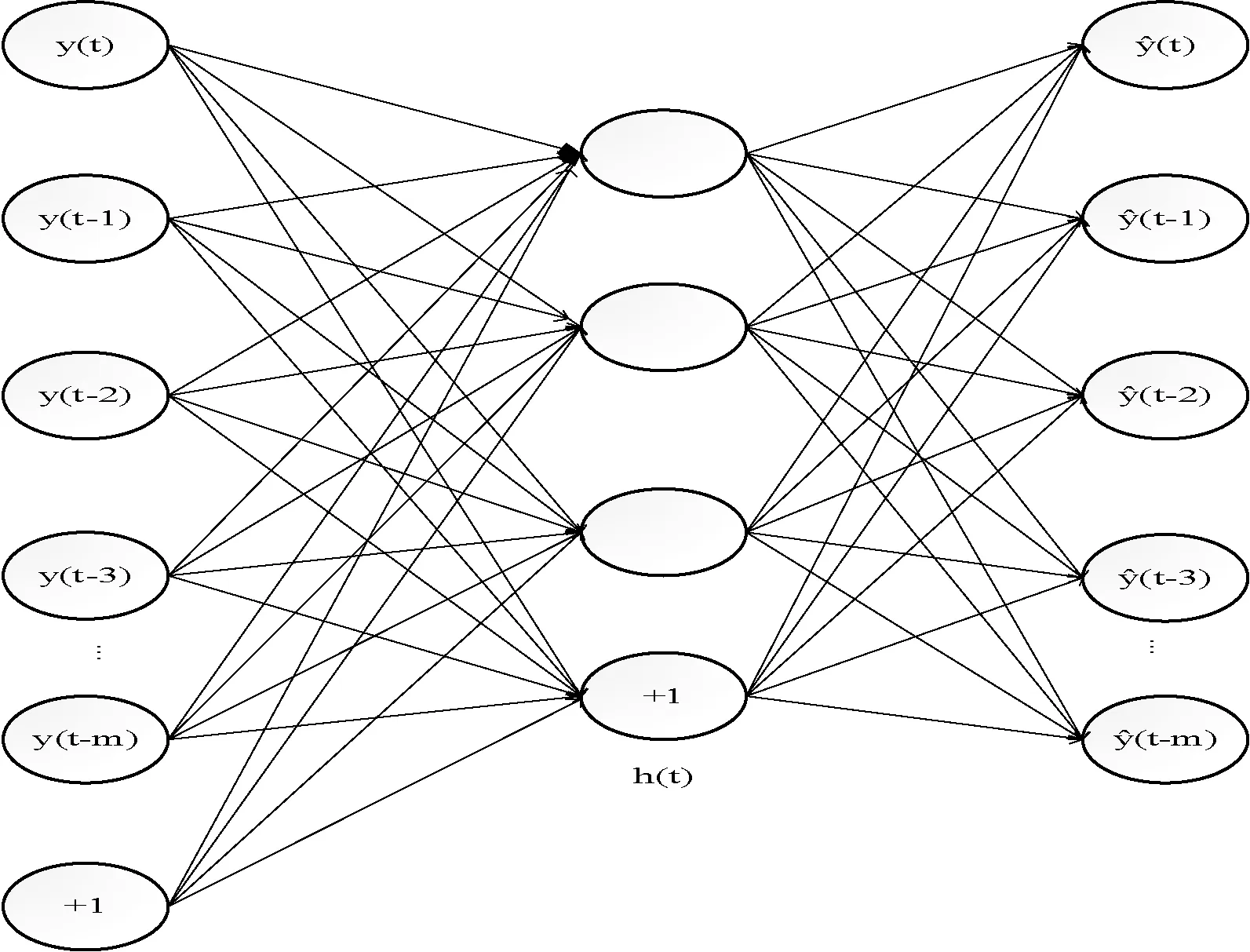
圖1 自編碼器的結構

設W1∈Rk×m、b1∈Rk分別表示可視層V(VisibleLayer)與隱藏層H(HiddenLayer)的連接權值和偏置，W2∈Rm×k、b2∈Rm分別表示隱藏層與重構可視層的連接權值和偏置。假定每一個節(jié)點非線性激活函數(shù)為sigmoid函數(shù)，則對于自編碼器的編碼過程如式(1)所示。

(1)

解碼過程為：

(2)

自編碼器將輸入y編碼為新的表達h，再將h解碼重構回y，通過反向傳播算法來訓練網(wǎng)絡實現(xiàn)重構并恢復輸入值。其關鍵在于求解參數(shù){w,b}使得重構誤差最小化。

若樣本數(shù)為N，則自編碼器輸出誤差代價函數(shù)可表示為：

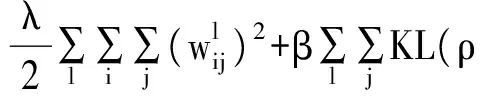
(3)

(4)

1.2SAE模型

通過堆疊n個自編碼器構成了棧式自編碼神經(jīng)網(wǎng)絡SAE(StackedAutoEncoder)，該模型中前一個自編碼的隱層輸出h(i-1)作為其后一層自編碼可視層的輸入V(i)，即：

V(i)=h(i-1)

其中i=2,3,…,n，即去除自編碼器的解碼層堆疊構成深度神經(jīng)網(wǎng)絡。n個自編碼器堆疊而成的SAE結構如圖2所示。

圖2 棧式自編碼器

SAE是對序列特征的學習過程，通過堆疊自編碼器，對序列進行深度學習，可以表達出序列間的潛在特征。

對于實現(xiàn)時間序列的預測目標而言，則需要再添加一個用于預測目標的神經(jīng)元，這一神經(jīng)元的目的在于通過監(jiān)督學習調整網(wǎng)絡模型以此實現(xiàn)預測目標。

1.3SAEP模型

對于時間序列{y(1),y(2),…,y(n)}，通過添加神經(jīng)元，在t時刻基于SAE的時間序列預測模型SAEP(StackedAutoEncoderbasedPredictionmodel)結構如圖3所示。

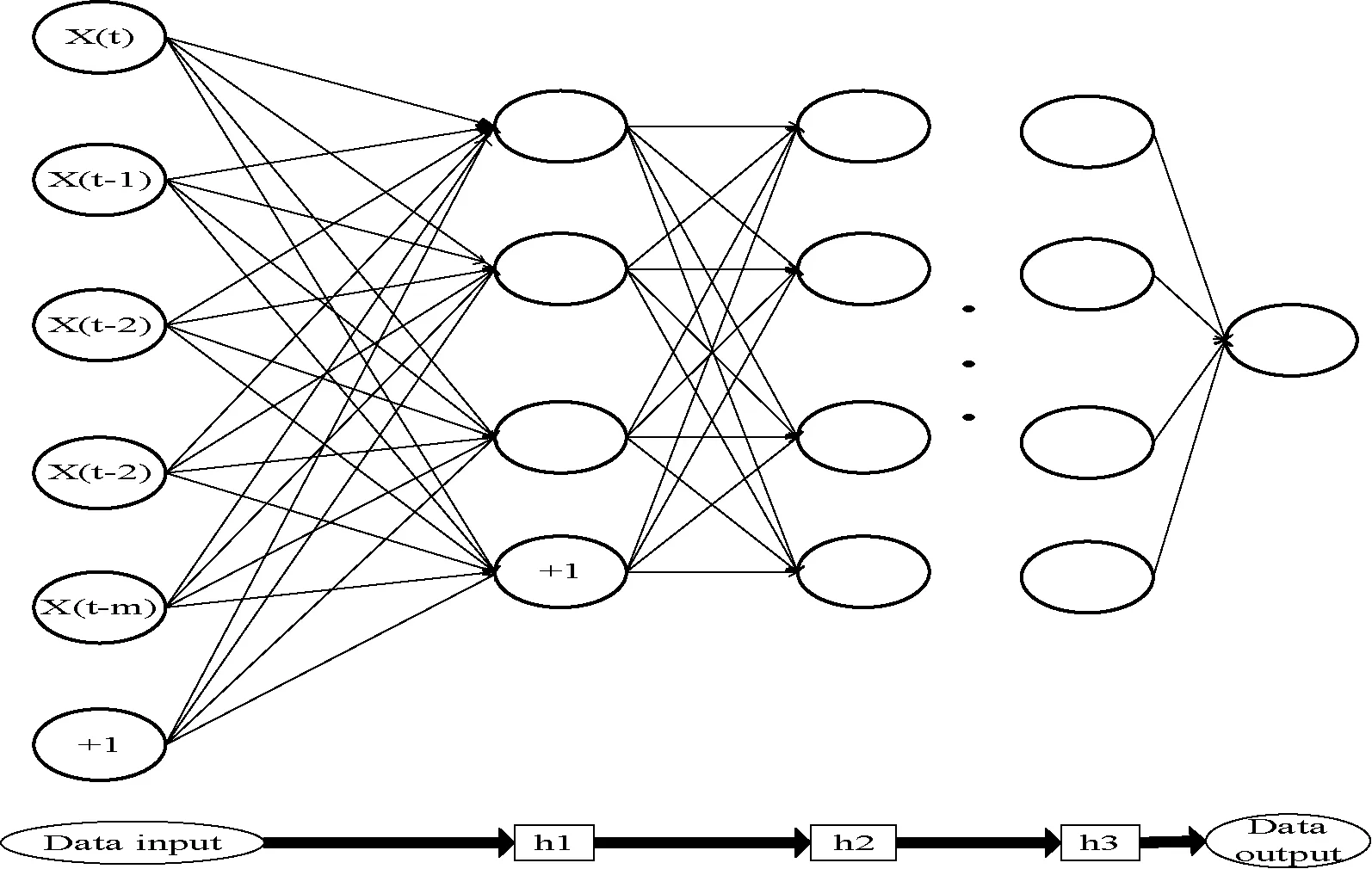
圖3 SAEP的結構

對于棧式自編碼神經(jīng)網(wǎng)絡，第1層的編碼器隱層特征為：

h(l)=σ(W(l)h(l-1)+b(l))

(5)

其中，h(0)=Y,W(l)和b(l)分別表示第1層自編碼器的編碼層權重和偏置。通過自編碼器的棧化多次非線性變換得到的h(n)表示了網(wǎng)絡學習到的潛在特征，它包含了預測目標中的重要信息。為了達到預測目標，以非線性sigmoid神經(jīng)元作為最后預測模型的輸出節(jié)點。

SAEP模型的整體代價函數(shù)為：

(6)

SAEP的關鍵是不斷調整{w,b}以此擬合出輸入輸出數(shù)據(jù)之間的函數(shù)關系。

2 SAEP模型的學習算法

基于以上的模型構建，SAEP的特征學習過程可以分為無監(jiān)督的預訓練，即SAE的特征學習，這一過程旨在挖掘出輸入序列的深層特征；基于監(jiān)督學習的預測，即深度神經(jīng)網(wǎng)絡的擴展(SAEP的構建)及網(wǎng)絡微調。

2.1 自編碼器的學習算法

自編碼器的參數(shù)學習采取反向傳播算法。在優(yōu)化神經(jīng)網(wǎng)絡時，首先利用式(1)和式(2)計算各層的神經(jīng)元激活值，根據(jù)式(3)計算代價函數(shù)，利用反向傳播算法計算各層代價函數(shù)的偏導數(shù)。假定自編碼器的輸出層為第L層,輸出目標為Y，自編碼器的輸出層和隱藏層各個節(jié)點的誤差表達式分別為：

δ(L)=-(Y-σ(z(L)))f′(z(L))

(7)

(8)

其中，l=L-1,…,2，式中的f為sigmoid函數(shù)，f′(z(l))表示第l層激活函數(shù)f(z)對輸入z的導函數(shù)值。按照下式計算l層神經(jīng)元節(jié)點的激活值：

z(l)=w(l)h(l-1)+b(l)

(9)

然后，根據(jù)以下公式計算需要的梯度：

▽w(l)E(W,b;x,y)=δ(l+1)(h(l))T

(10)

▽b(l)E(W,b;x,y)=δ(l+1)

(11)

利用梯度下降法更新權重參數(shù)，設α為每次迭代的學習率，迭代更新表達式為：

w(l)=w(l)-α[▽w(l)E(W,b;x,y)]

(12)

b(l)=b(l)-α[▽b(l)E(W,b;x,y)]

(13)

通過不斷反復迭代以此減小代價函數(shù)式(3)的值，以此來優(yōu)化自編碼器。

2.2 逐層貪婪學習算法

棧式自編碼器若采取梯度下降法，往往并不能取得很好的效果，主要原因在于網(wǎng)絡深度的增加會使得反向傳播的梯度值急劇減小，因此在最初的幾層網(wǎng)絡權值的導數(shù)非常小，即權值變化非常緩慢，以至于無法訓練[15]。為避免訓練出現(xiàn)局部最優(yōu)，SAE的實現(xiàn)采取逐層貪婪學習算法[15]。該算法的主要思想在于每次只訓練網(wǎng)絡中的一層，首先訓練一個只含一個隱藏層的自編碼器，該層自編碼器達到優(yōu)化后再開始訓練下一個自編碼器。利用逐層貪婪學習算法完成SAE無監(jiān)督預訓練。

2.3SAEP微調

無監(jiān)督預訓練之后，如圖3所示構建SAEP模型，微調策略為監(jiān)督學習機制。微調以圖3為網(wǎng)絡結構模型，將所有層視為一個網(wǎng)絡整體，以SAE預訓練結果為初始權值。利用式(5)、式(6)前向傳播計算各個層神經(jīng)元節(jié)點的激活函數(shù)值和整體代價函數(shù)，再利用反向傳導算法計算式(7)-式(13)(此時式(8)的β=0，其他相應的損失函數(shù)為J(w,b)),通過反復迭代梯度下降法更新權重參數(shù)，以此使得SAEP的代價函數(shù)式(6)達到最小。

3 實驗設計與分析

此次實驗的軟件平臺為MATLABR2014a，編程實現(xiàn)算法。

模型的評價標準為式(14)、式(15)表示的均方偏差、平均偏差率。

(14)

(15)

實驗數(shù)據(jù)來源于經(jīng)典數(shù)據(jù)庫TimeSeriesDataLibrary，來源于真實的金融市場(https://datamarket.com/data)。8個數(shù)據(jù)集為1979年12月31日—1998年12月31日JPY/USD(日本/美國)、French/US(法國/美國)、German/US(德國/美國)、Australia/US(澳大利亞/美國)、British/US(英國/美國)Canadian/US(加拿大/美國)、Dutch/US(荷蘭/美國)、Swiss/US(瑞士/美國)匯率時間序列。

實驗中，對所有實驗數(shù)據(jù)均按式(16)進行[0,1]上的歸一化預處理。然后采取單變量滑動窗口機制訓練數(shù)據(jù)，樣本總數(shù)為4 774，隨機抽取80%作為訓練樣本，20%作為測試樣本。本次實驗在不同數(shù)據(jù)集模擬20次，并對測試集結果取平均值。

(16)

表1為在不同數(shù)據(jù)集下SAEP的預測效果。從表中可看出，模型的預測誤差均控制在較低的水平，其預測耗時均在1 s以內，能夠很好地滿足實時預測中對預測時間和預測精度的高要求。此外，在實驗中算法在不同的數(shù)據(jù)集下均能夠保證100次以內得到收斂，收斂較快的特點保證了模型在不同數(shù)據(jù)集的穩(wěn)定性。

表1 不同數(shù)據(jù)集的測試集預測效果

續(xù)表1

為了充分反應模型的效果，以日/美測試數(shù)據(jù)集為例，對比目前在匯率時序預測中得到普遍應用的BP神經(jīng)網(wǎng)絡和SVR。如表2所示。

表2 不同預測模型的測試預測效果

不難發(fā)現(xiàn)，SAEP的預測效果優(yōu)于BP神經(jīng)網(wǎng)絡和SVR。BP神經(jīng)網(wǎng)絡被證明可以以任意精度逼近任意的函數(shù)，但其隨機初始化時導致結果不夠穩(wěn)定，泛化能力表現(xiàn)欠佳。通過三種模型的對比可以看出，SAEP的表現(xiàn)能力更強。

4 結 語

棧式自編碼器預測模型改進了神經(jīng)網(wǎng)絡隨機初始化的缺點，有效地表達出序列數(shù)據(jù)間非線性及隨機性的特點，自編碼器在神經(jīng)網(wǎng)絡的預訓練對于提高預測效果具有重要意義；SAEP的微調作用以監(jiān)督機制通過反向傳導算法調整網(wǎng)絡，這對于預測目標起到了關鍵的作用，無監(jiān)督學習對于時間序列的實時預測具有重要的應用研究和推廣價值。

但是反向傳導算法在網(wǎng)絡層次過深時會出現(xiàn)梯度擴散現(xiàn)象，因此本文提出的棧式自編碼預測模型更適合于低配置計算資源中網(wǎng)絡層次不是特別深的預測中。

[1] 劉金培,林盛,郭濤,等.一種非線性時間序列預測模型及對原油價格的預測[J].管理科學,2011,24(6):104-122.

[2]MartinLangkvist,LarsKarlsson,AmyLoutfi.Areviewofunsupervisedfeaturelearninganddeeplearningfortime-seriesmodeling[J].PatternRecognitionLetters,2014(42):11-24.

[3] 王知音,禹龍,田生偉,等.基于棧式自編碼的水體提取方法[J].計算機應用,2015,35(9):2706-2709.

[4]BengioY,CourvilleA,VincentP.LearningdeeparchitectureforAI[J].FoundationsandTrendsinMachineLearning,2009,2(1):1-127.

[5] 鄧侃,歐智堅.深層神經(jīng)網(wǎng)絡語音識別自適應方法研究[J].計算機應用研究,2016,7:52-56.

[6] 周慧,周良,丁秋林.基于深度學習的疲勞狀態(tài)識別研究[J].計算機科學,2015,42(3):191-200.

[7] 姚利濤,董育寧.無監(jiān)督的視頻業(yè)務特征分析與分類[J].應用科學學報,2015,33(2):117-128.

[8]SantoAAP,CostaJNCA.Computationalintelligenceapproachesandlinearmodelsincasestudiesofexchangerate[J].ExpertsSystemswithApplications,2007,33(4):816-823.

[9]EtteHarrisonEtuk.AseasonalARIMAmodelfordailyNigerianNAIRA-USDollarexchangerates[J].AsianJouralofEmpiricalResaerch,2(6):219-227.

[10]MichaelMckenzie,HeaherMitchell.GeneralizedasymmetricpowerARCHmodellingofexchangeratevolatility[J].AppliedFinancialEconomics,2002,12(8):555-564.

[11] 劉潭秋,謝赤.基于GRACH模型和ANN技術組合的匯率預測[J].科學技術與工程,2006,6(23):4690-4694.

[12]ChenAS,LeungM.RegressionNeurralNetworkforErrorCorrectioninForeignExchangeForecastingandTrading[J].Computers&OperationsResearch,2004,31(7):1049-1068.

[13]ChakradharaPanda,VNarasimhan.ForecastingExchangeRateBetterwithArtificialNeuralNetwork[J].JournalofPolicyModeling,2007,29(2):227-236.

[14]CaoLJ.Supportvectormachinesexpertsfortimeseriesforecasting[J].Neurocomputing,2003,51:321-339.

[15]HintonGE,OsinderoSYW.TheAfastlearningalgorithmfordeepbeliefnets[J].NeuralComput,2006,10(7):1527-1544.

EXCHANGE RATE TIME SERIES PREDICTION BASED ONSTACKED AUTOENCODER MODEL

Kou Xixi1He Xiping1,2,3*

1(ChongqingKeyLaboratoryofElectronicCommerceandSupplyChain,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)2(SchoolofComputerScienceandInformafionEngineering,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)3(ChongqingDetectionControlIntegratedSystemEngineeringLaboratory,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)

Aiming at the current problem of limited prediction accuracy of nonlinear financial time series in the shallow model, a novel prediction model of stacked autoencoder neural networks is proposed, consisting of stacked autoencoder model at the bottom and regression neurons at the top. First of all, the unsupervised learning mechanism of autoencoder is applied to identify and learn the features of time series, greedily learning the neural network layer by layer. Then the stacked autoencoder is extended to be the SAEP model with supervision mechanism, and the parameters learned by SAE (stacked autoencoder) are used to initialize the neural network. Finally, the weights are fine-tuned by supervised learning. The experimental design uses the exchange rate time series as the training and test samples, and the effectiveness of the proposed model in the application of exchange rate time series prediction is verified, compared with the more mature methods.

Time series Prediction Deep learning Stacked autoencoder Feature learning Deep neural networks

2016-03-02。重慶市教委科技

KJ1400612)；重慶工商大學研究生院“創(chuàng)新型科研項目”(yjscxx2015-41-21)。寇茜茜，碩士生，主研領域：機器學習。何希平，教授。

TP391 TP183

A

10.3969/j.issn.1000-386x.2017.03.039