電力系統最優觀測方案的研究
旋艷超 李麗 劉昊利
(1.國網朝陽供電公司電氣試驗班,遼寧朝陽 122000;2.國網阜新供電公司運維采集班,遼寧阜新 123000)
電力系統最優觀測方案的研究
旋艷超1李麗2劉昊利1
(1.國網朝陽供電公司電氣試驗班,遼寧朝陽 122000;2.國網阜新供電公司運維采集班,遼寧阜新 123000)
基于系列繁雜測量的電力系統觀測問題是狀態預測前的必要步驟,同時,狀態的準確預測程度直接關系到系統安全操作的重要性。針對此,提出一種改進型的電氣優化解決方案,即友好整數線性規劃法。通過現場實際例子說明了該方案的計算高效性,通過與傳統試驗分析數據的統計與比對,證明了該整定方案的實際效力。
電力系統;觀測方案;整數試驗;線性;響應時間
為保證控制中心可監控與操作的電力系統安全,控制中心的操作器需要知道任一瞬間系統的準確狀態,系統狀態的描述可有系統觀測器得到。
狀態觀測器是一種數學算法,通過具體數據得到測量值,實時計算出系統最有可能出現的狀態。如果測量設備的位置和數據不正確,狀態觀測器就不能計算出準確的系統狀態,導致一些線路的狀態便不可知[1]。所以,在系統觀測之前首先要知道系統是否可觀,以及測量裝置能否觀測所有的線路狀態。如果系統不可觀,則連接觀測點和不可觀分支的信息需要同時齊備。
傳統方式上,觀測問題都是從代數和拓撲角度加以考慮。分析增廣矩陣,計算格拉姆矩陣,研究雅可比矩陣的零空間,或是借助于圖論[2]。然而,現下的科技手段容許通過整數規劃問題來解決此觀測問題。此方案對問題的解決看起來會有些出入,但在具體例子中會得以論證。此外,仿真結果也說明在含有大量線路的系統計算效率上,該方案更勝一籌。
本文的核心目的在于構建整數線性規劃法,其最優解決方案取決于電氣系統是否可觀測以及可觀或不可觀變量的個數[3]。同時基于改進型最優規劃,提出一種區分不可觀支路與可觀點個數的方案。
1 最優狀態觀測方案
解決最優觀測問題的關鍵在于觀測技術的合理應用。在此方案的構建中,每條線路的狀態變量觀測模型使用二維變量,并可選用任意矢量K作為觀測矢量,每次測量的矢量K都含有一些限定條件[4]。比如,系統準實時信息、線路電壓值、有功潮流與無功潮流值、有功潮流與無功潮流的注入值,以及總線電壓的幅角。并認為K是獨立矢量,相應記為(K)=1。繼而討論最優變量、目標函數和等式限定條件[5,6]。
1.1 最優變量
設計模型的最優變量用于定義每條線路狀態變量的觀測裕度。對于每條線路而言,有2種狀態變量去預測狀態觀測算法,即為電壓值與幅角[7]。因此,與第i條線路的2種狀態變量觀測裕度相關的最優變量定義如下:bvi=0,第i條線路的電壓值不可觀;bvi=1,第i條線路的電壓值可觀;bθi=0,第i條線路的電壓幅角不可觀;bθi=1,第i條線路的電壓幅角可觀。
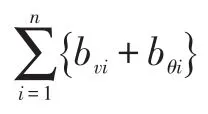
同時,要考慮到如果測量矢量是由成對出現的有功功率或無功功率的測量因子構成,則意味著可選用二分法來解決相應問題,從而相應減少中央處理器在計算上的響應時間[9]。如果系統分析的問題是可觀測的,則意味著狀態觀測方法可由最優化分析方案得到。
1.2 可觀測點與不可觀分支的區分
不可觀測點是由內部相連接的分支構成,分支上的能流可通過測量矢量K獲得,可觀測點可通過不可觀測分支連接其他可觀測點,不可觀測分支的能流則是不能被預測的[9,10]。因此,不可觀系統是由一些可觀測點及連接可觀測點間的不可觀分支線路構成。可觀測點與不可觀測分支也同樣可以由任意矢量標記[11]。
2 改進方案分析
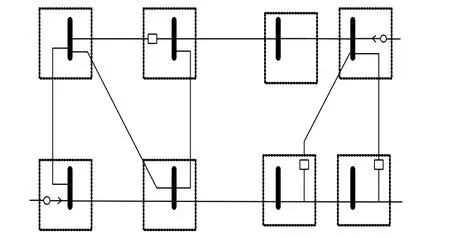
圖18 總線系統測量圖
圖2提供了整數線性規劃法與傳統解矩陣算法相比較下的中央處理器平均響應時間曲線。值得一提的是,從試驗數據曲線的生成結果可以看出,8條線路的系統響應時間與精確度較之傳統的最優觀測方法都有很大程度的提高,說明系統的電氣特性得到了一定改觀。
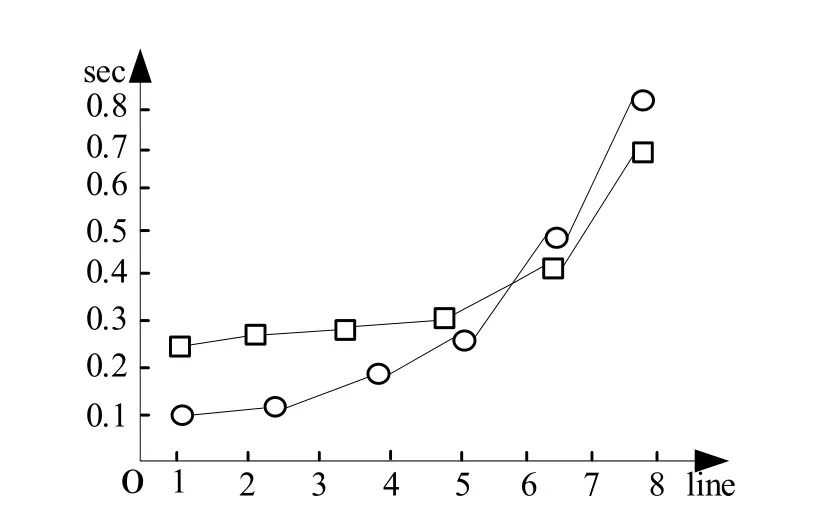
圖2 中央處理器響應時間曲線
3 結論
本文提出的整數線性規劃法可有效區分電力系統的可觀變量,該數學模型使用的線性及雙變量建模方法顯示了該整定方案在數據處理方面的高效性與精確性。通過與傳統觀測方法在處理器響應時間上的比對,說明了該建模方案的計算數值精確可靠、高效快捷。
[1]FF Wu,WHE Liu,SM Lun.Observability analysis and bad data processing for state estimation with equality constraints[J].IEEE Transactions on Power Systems,1988(2):541-548.
[2]吳杰康,史美娟,陳國通,等.基于Multi-AIGA算法的區域電力系統最優備用模型[J].電力系統及其自動化學報,2008(2):51-56.
[3]R Rouhani,RK Mahra.Model algorithmic control(MAC);basic theoretical properties[J].Automatica,1992(4):401-404.
[4]席裕庚,耿曉軍,陳虹.預測控制性能研究的新進展[J].控制理論與應用,2000(4):469-475.
[5]B Gou.Jacobian matrix-based observability analysis for state estimation[J].IEEE Transactions on Power Systems,2006(1):348-356.
[6]李文沅,周家啟,顏偉,等.基于可靠性的電力系統設備備用規劃方法[J].中國電機工程學報,2006(15):7-11.
[7]RL Chen.A fast integer algorithm for observability analy?sis using network topology[J].IEEE Transactions on Power Sys?tems,1990(3):1001-1009.
[8]Ionescu V,Oara C.Spectral and inner-outer factorization for discrete-time systems[J].IEEE Transactions on Automatic Con?trol,1996(12):1840-1845.
[9]于洋,陳琳,甘德強,等.國內外備用容量評估方法比較[J].電力系統自動化,2005(18):19-23.
[10]吳集光,劉俊勇,牛懷平,等.電力市場環境下最優備用容量的確定[J].電力系統自動化,2005(15):10-13.
[11]任震,潘錫芒.電力市場中計及發電機組可用率的備用分配計算[J].電力系統自動化,2002(17):16-18.
[12]王建學,王錫凡,丁曉瑩.區域電力市場中的分區備用模型[J].中國電機工程學報,2006(18):28-33.
Research of the Power System Optimal Observation Scheme
Xuan Yanchao1Li Li2Liu Haoli1
(1.Electric Experimental Work Area,Sate Grid Chaoyang Power Supply Co.Ltd.,Chaoyang Liaoning 122000;2.Operation Collection Work Area,Sate Grid Fuxin Power Supply Co.Ltd.,Fuxin Liaoning 123000)
Power system observation based on a series of complex measurement is a necessary step ahead of state fore?casting,at the same time,the level of state predict is much relative with safety operation.So this paper proposed a modified solution to the problem,namely friendly integer linear programming method.The computation efficiency of the scheme has been proved through the actual examples,as well as proved that the actual effect of the setting scheme through the statistics and compare with the traditional experimental analysis data.
power system;observation scheme;integer test;linear;required time
TM73
A
1003-5168(2017)02-0137-02
2017-01-15
旋艷超(1985-),男,技師,研究方向:高壓試驗領域研究。

