雙饋風力發電系統矢量控制研究

許湖江

上海交通大學 電子信息與電氣工程學院　上海　200240

雙饋風力發電系統矢量控制研究

許湖江

上海交通大學 電子信息與電氣工程學院上海200240

基于定速與變速風電系統的運行特性，得出了變速風力發電系統的優點。在變速風力發電系統工作原理的基礎上，提出了動態模型方程，并論述了雙饋風力發電系統的矢量控制理論。對 1.5MW 雙饋風力發電系統進行了計算機仿真與實際運行試驗，驗證了所論述理論的正確性。

風力發電；矢量控制；仿真；試驗

1　研究背景

為應對日益凸顯的環境危機及能源危機[1]，作為可再生能源中最成熟的技術，風力發電得到了全球各國的高度重視。風力發電系統的目的是最大限度獲取風能，提高風力發電機組的輸出功率。2000年前，風力發電機組單機輸出功率還只是千瓦級別，最大額定功率只有200kW，但是到了2000年之后，市場上主流的風力發電機組輸出功率達到了兆瓦級別。預計在不久的將來，風力發電機的額定功率將進一步增大，特別是在海上風電的應用中。2016年，兩大風電巨頭維斯塔斯與西門子在歐洲安裝了各自研發的 8MW 樣機，使國際海上風電正式進入了8MW時代。目前市場上主流的風力發電機參數見表1，這些風力發電機均為變槳距及變速控制。

表1　主流風力發電機參數

早期安裝的小容量風力發電系統，選用簡單的鼠籠式異步感應發電機，將風能轉化為電能直接連接至三相電網，其風輪轉子通過固定傳動比率的齒輪箱直接連接到發電機主軸上。也有一些感應發電機使用極點可調的繞組配置來實現風力發電機在不同同步轉速下的運行。上述類型的風力發電機必須在恒定速度下運轉，不能變速運行，這種恒速風力發電系統的結構及性能非常依賴于機械結構的設計及電力電子電路的特性。由于風能特有的不確定性，每當一陣風吹到風力發電機組上時，可以看到系統的輸出功率會有一個非常快速且強烈的變化。負載的變化不僅需要一個穩定的電網系統來維持，而且需要非常穩固的機組機械結構來吸收變化過程中產生的高機械應力，尤其是對于額定功率比較高的機組，使用恒速風電系統會導致成本昂貴。因此，目前市場上的主流設計為變速風力發電系統。

2　變速風力發電系統

目前市場上主流的大容量風力發電機組大都采用變速運行的技術方案[2]，與恒速風力發電機組相比，變速風力發電機組具有以下主要優點。

(1) 具有顯著的成本效益，可對槳距角進行控制[3]。發電機的控制速度可以允許槳距角控制時間變得更長，從而降低變槳距控制的復雜性，以及峰值功率要求。當在低風速情況下時，槳距角通常是固定的；而當處于超過額定功率對應的風速時，執行槳距角控制，最終限制機組最大功率的輸出。

(2) 降低機組運行時的機械應力，吸收偶然性陣風，能量可以被儲存在風力發電機的機械慣性中，從而減小機械轉矩的振蕩。

(3) 提高電能質量，減小輸出功率的瞬間變化。

(4) 提高系統的工作效率，使風力發電機組始終在最大功率點附近運轉[4-5]。

(5) 降低風力發電機運行的噪聲。

3　雙饋風力發電系統

變速恒頻雙饋風力發電系統是目前風電行業應用最廣泛、技術最成熟的風電技術之一。圖1為典型的變速恒頻雙饋風力發電系統，系統中包括了雙饋發電機、功率變換器等部件。雙饋發電機的定子端直接與電網相連接，轉子端則通過一組交-直-交背靠背脈寬調制變流器與電網相連，變流器為轉子繞組提供勵磁電流。根據雙饋發電機定轉子的電磁關系可知，變流器只需要提供轉差功率，即最大30%額定功率便可實現雙饋風力發電系統的變速恒頻運行與最大功率追蹤[6]，大大降低了變流器的容量，節約了成本。此外，通過改變勵磁電流的相位與幅值，可以實現發電機輸出有功功率與無功功率的解耦控制，提高風電場功率調度的靈活性。

3.1　數學模型

為了研究雙饋風力發電系統的動態性能，以及有功無功功率的解耦控制[7]，需要討論雙饋風力發電系統的動態數學模型。由于雙饋風力發電機與普通繞線式異步發電機在電機結構方面類似，因此可以參考普通異步發電機的理論進行分析與研究。設雙饋風力發電機定子端正方向采用發電機慣性，轉子端正方向采用電動機慣性，基于磁勢與電勢平衡理論，可以得到雙饋風力發電機的等效電路，如圖2所示，其數學基本方程式為：

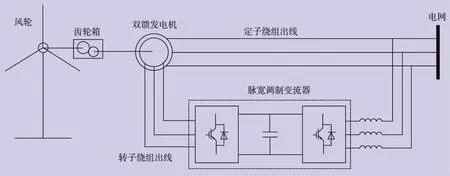
圖1　典型變速恒頻雙饋風力發電系統

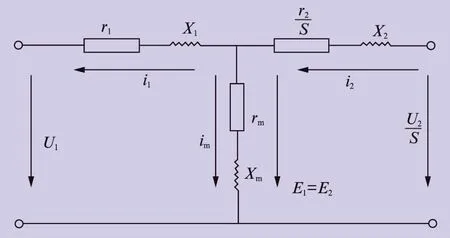
圖2　雙饋風力發電機等效電路

(1)

式中：U1為定子側電源電壓；U2為轉子側饋電電壓；E1為定子側感應電動勢；S為發電機轉差率；E2為轉子側感應電動勢；Em為互感感應電動勢；i1為定子電流；i2為轉子電流；im為互感電流；r1與X1分別為定子繞組電阻與漏抗；r2與X2分別為轉子繞組電阻與漏抗；rm與Xm分別為勵磁互感回路電阻與漏抗。

當機組的額定電壓、額定功率及功率因數一定時，雙饋風力發電機實際上只有S、U2，以及U2與U1相位差角度之間的關系，即可通過調節雙饋發電機組幅值、頻率及相位來控制輸出。

由雙饋風力發電系統在三相靜止坐標系下的物理模型，可以得到機組在三相靜止坐標系下的數學模型。在該數學模型中，雙饋風力發電機定子與轉子的互感應與轉子位置角有關，發電機數學模型為時變非線性、高階微分方程，磁鏈則具有強耦合關系，電感的矩陣較復雜，很難得到它的解析解，想要對雙饋風力發電系統進行控制就更加困難了。因此基于以上考慮，對雙饋風力發電系統數學模型進行簡化，并進行解耦磁鏈。

將三相靜止坐標系變換到d-q兩相同步參考坐標系，這一等效變換是在磁勢一致的前提下進行的。在完全對稱的三相靜止繞組中，三相交流電流過后可疊加為一個旋轉磁勢F，該磁勢按照正弦分布的形式在空間中以同步轉速ω1，即電流角頻率進行旋轉，不同相的繞組可認為在相應的坐標系上所產生的磁勢F是相同的。通過以上方法，雙饋風力發電系統的數學模型可以得到較大簡化。

一般情況下，將三相靜止繞組等效為兩個相同匝數并且互相垂直的旋轉繞組d1、q1，當d、q兩軸的電流id1與iq1流過這兩個繞組時，合成的磁勢相對于d1、q1繞組是靜止的，所以合成磁勢等效為一個空間的磁勢。通過控制d1、q1繞組中流過的電流大小來控制旋轉磁場的轉速和大小，從而保持與坐標系下的旋轉磁勢F相一致，這樣就達到了使用旋轉d1、q1繞組來取代三相靜止繞組的目的。圖3為旋轉d-q坐標系下的雙饋風力發電機繞組等效物理模型，其中uq1s、uq1r、ud1s、ud1r對應代表雙饋風力發電機定轉子繞組在d、q軸上的電壓。

圖3　旋轉d-q坐標系下雙饋風力發電機繞組等效物理模型

依據坐標變換，在保證磁勢不變的情況下，三相靜止坐標系變換到d-q坐標系的數學矩陣ks(θ)為：

(2)

式(2)中θ為靜止坐標系A軸與d-q坐標系d軸的夾角，并隨時間的改變而改變。

d-q坐標系的旋轉角速度ω=dθ/dt，同時ω=ω1。

經過坐標變換，由式(1)、式(2)轉換可得d-q坐標系下的電流方程為：

(3)

式中：iq1s為q軸定子繞組電流;Xls為定子電抗;Xlr為轉子電抗;Ψq1s為q軸定子磁通;Ψmq1為q軸互感磁通;id1s為d軸定子繞組電流;Ψd1s為d軸定子磁通;iq1r為q軸轉子繞組電流;Ψq1r為q軸轉子磁通;id1r為d軸轉子繞組電流;Ψd1r為d軸轉子磁通。

互感磁通的方程為：

(4)

式中：Ψmd1為d軸互感磁通；Xm1為互感勵磁電抗。

磁通方程為：

(5)

式中：ωb為電磁場旋轉角速度；ωr為轉子旋轉角速度；Xaq1和Xad1分別為q、d軸電樞反應電抗參數。

(6)

電磁轉矩Te方程及轉子旋轉角速度方程分別為：

(7)

(8)

式中：TL為作用于軸上的機械轉矩；J為電機轉動慣量；P為發電機極對數。

3.2　矢量控制

雙饋風力發電系統是一個多變量、強耦合、復雜多變的非線性系統，需要對雙饋風力發電機組的數學模型進行解耦控制，而矢量控制則是實現解耦的關鍵技術。雙饋風力發電機定轉子的電流分量為工作頻率量和轉差頻率量，它是一個高階非線性強耦合多變量系統，如果簡單地對交流電進行閉環控制而不進行解耦，得到的效果并不理想。矢量控制可在坐標變換理論的基礎上，使雙饋風力發電機內部各變量之間的耦合關系得到簡化，從而可使雙饋風力發電機的控制得到簡化。

雙饋風力發電系統應用矢量控制策略，解耦電磁轉矩和轉子勵磁控制，使q軸的定子磁通量得到消除，由此，電磁轉矩方程式可以寫為：

Te=-3PXm1imsiq1r/2

(9)

式中：ims為定子側互感勵磁電流。

由式(9)可以得出，Te能通過控制q軸轉子繞組電流iq1r來直接控制雙饋風力發電機的轉子轉速，因此，對于一個給定的輸入機械轉矩TL，雙饋風力發電機的輸出功率就能被控制。無功功率的控制也可以由q軸轉子繞組電流iq1r來實現控制。

為確保系統的穩定運行，并能獨立控制雙饋風力發電機組的有功與無功功率輸出，設計了雙饋風力發電系統矢量控制器，如圖4所示。

圖4中IRdq和VRdq分別為兩相d-q坐標系下的轉子電流與電壓，IS dq為兩相d-q坐標系下的定子電流，VR和IR分別為雙饋風力發電機側變流器轉子電壓與電流，VS和IS分別為電網側變流器定子電壓與電流，VDC為變流器直流母線電壓，PG和QG分別為雙饋風力發電機的有功和無功功率，PGset和QGset分別為雙饋風力發電機的有功和無功功率參考值，ΦVS和ΦVR分別為雙饋風力發電機定子和轉子電壓矢量角，IGC為電網側變流器控制電流，IN為雙饋風力發電機額定電流。

根據圖4測量得到的轉子電流信號可用于轉子電流的調節，以減小參數失諧，以及變流器增益誤差的影響。

4　仿真結果

為了評估雙饋風力發電系統矢量控制[8-9]的效果，基于MATLAB軟件Simulink仿真模塊，對雙饋風力發電系統進行了仿真模擬分析[10]。圖5為雙饋風力發電系統在不同轉速比下的瞬時有功功率隨時間變化響應曲線。由圖5(a)可知，當解耦控制未被激活，即使用基于滑移控制的基本穩態電壓模型來控制機組系統時，由于d、q兩軸變量之間的耦合，系統性能取決于響應速度。由圖5(b)可知，根據雙饋風力發電系統的動力學模型進行解耦控制時，系統響應的速度較快且平穩。

5　試驗結果

在國產典型1.5MW雙饋風力發電機組上進行試驗，系統的額定功率為1.5MW，雙饋風力發電機額定轉速為1800r/min，試驗結果如圖6～圖10所示。

圖4　雙饋風力發電系統矢量控制器

圖5　雙饋風力發電系統在不同轉速比下的瞬時有功功率隨時間變化響應曲線

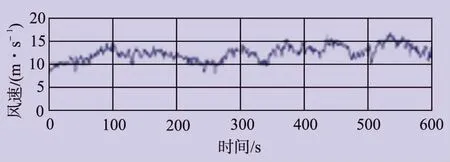
圖6　運行試驗風速波形

圖7　運行試驗轉子轉速波形

圖8　運行試驗變槳角度波形

圖9　運行試驗轉矩指令百分比波形

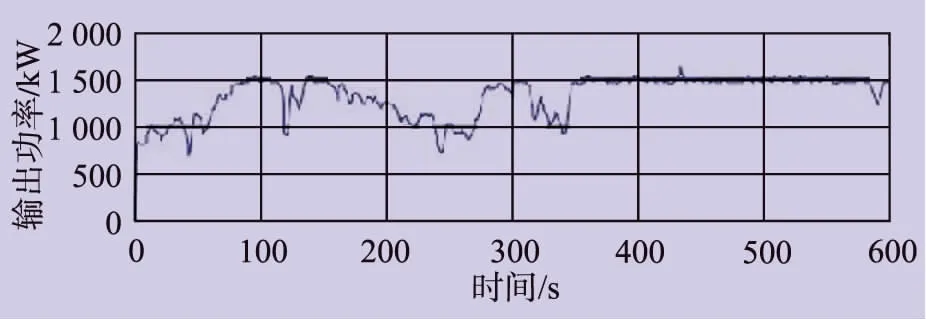
圖10　運行試驗輸出功率波形

機組主要使用變槳控制來控制風力發電機的轉速。當時間為350s時，由于機組未達到最大輸出功率，此時變槳控制不是很有效，因此，系統跟蹤最大功率曲線來達到最大功率輸出。當時間長于350s時，可看到風速達到15m/s，機組系統將轉矩指令百分比限制在100%，且系統傳輸到電網的實際輸出功率完美匹配了設定的控制指令。在恒定最大功率模式下，變槳系統將風輪葉片速度控制在一定范圍內，在短時間內風速達到18m/s，但變槳控制系統并沒有跟蹤陣風。在此瞬態過程中，輸出功率幾乎保持恒定，保證了電能質量，維護了電網的穩定。

6　結論

對于大容量并網型風力發電系統，使用變速調節風力發電機組是最理想、最具經濟效益的技術方案。

筆者推導了雙饋風力發電系統數學模型，設計了矢量控制器，并以此來解耦及對無功功率進行控制，仿真結果及1.5MW雙饋風力發電機組實際運行試驗數據驗證了理論的正確性。

[1] 羅承先.世界風力發電現狀與前景預測[J].中外能源，2012,17(3): 24-31.

[2] 譚超.變速恒頻雙饋風力發電系統控制技術研究[D].長沙： 湖南大學，2013.

[3] 繆新磊，秦棟平.運動控制在變槳控制系統中的應用[J].上海電氣技術，2016，9(2)： 49-51，63.

[4] 劉其輝，賀益康，趙仁德.變速恒頻風力發電系統最大風能追蹤控制[J]．電力系統自動化，2003，27(20)： 62- 67.

[5] 賀益康，胡家兵.雙饋異步風力發電機并網運行中的幾個熱點問題[J].中國電機工程學報，2012,32(27): 1- 15.

[6] 辜承林，韋忠朝，黃聲華，等．對轉子交流勵磁電流實行矢量控制的變速恒頻發電機——(第一部分： 控制模型與數值仿真)[J]．中國電機工程學報，1996，16(2)： 119-124.

[7] 劉新宇.大型雙饋風力發電機組并網轉子勵磁控制技術研究[D].鄭州： 鄭州大學，2013.

[8] 孫佳林，奚玲玲．兆瓦級風力發電機運行流程與安全策略的研究與實踐[J]．上海電氣技術，2009，2(4)： 33- 36.

[9] TANG Y， XU L. A Flexible Active and Reactive Power Control Strategy for a Variable Speed Constant Frequency Generating System[J]. IEEE Transactions on Power Electronics，1995，10(4)： 472-478.

[10] 訾鵬，周孝信，田芳，等．雙饋式風力發電機的機電暫態建模[J].中國電機工程學報，2015，35(5): 1106- 1114.

(編輯： 平平)

Based on the operating characteristics of fixed speed wind power system and variable speed wind power system, the advantages of variable speed wind power generation system were obtained. Based on the working principle of variable speed wind power generation system, the dynamic model equation was put forward, and the vector control theory of DF wind power generation system was discussed. The computer simulation and practice service test of 1.5 MW DF wind power generation system were carried out to verify the validity of the theory.

WindPowerGeneration；VectorControl；Simulation；Test

TM315

A

1674-540X(2017)04-021-06

2017年5月

許湖江(1986—)，男，本科，工程師，主要研究方向為風力發電系統控制與技術，E-mail: xuhj198603@163.com