區間值模糊決策序信息系統的分布約簡*

史德容，徐偉華

重慶理工大學 理學院，重慶 400054

區間值模糊決策序信息系統的分布約簡*

史德容，徐偉華+

重慶理工大學 理學院，重慶 400054

粗糙集；區間值；序信息系統；分布約簡

1 引言

粗糙集理論[1-2]最早由數學家Pawlak在1982年提出，是數據分析的一種數學工具，是經典集合論的一種推廣形式，其主要思想是在保持分類不變的情況下，經過屬性約簡推出問題的決策準則。目前，國內對粗糙集的理論基礎及應用[3-4]研究取得了很大的進步，許多學者已在該領域出版了相應的專著，同時也發表了數百篇論文。當然粗糙集[5-6]的應用不僅僅是限制在知識理論方面，它已經在人工智能、故障檢測、數據挖掘、醫療診斷、股票數據分析、模式識別、智能信息處理等領域得到了普遍的應用。

粗糙集理論的核心問題之一就是知識約簡[7-9]。約簡就是實際的知識庫中所描述的知識的屬性并不都是同等重要的，甚至有些屬性是多余的。所謂知識約簡，就是從知識庫中去掉一些不重要的屬性，使得知識得以簡化，又不丟失其主要信息。

實際問題中，事物的一些屬性值介于某個范圍之間，常被用來刻畫信息系統[10]中的不確定信息。為了表達這種情況，屬性值通常用區間值[11-12]形式來表示，進一步將其模糊化，這種信息系統就是區間值模糊信息系統。本文通過在帶有決策的區間值模糊信息系統中引入優勢關系[13-16]，建立區間值模糊序信息決策系統；在不協調的區間值模糊序信息系統[15-17]中引進了分布約簡以及最大分布約簡[18]，探討二者之間的關系，得到了分布約簡和最大分布約簡的判定定理以及辨識屬性集和可辨識矩陣；提供了不協調的區間值模糊序信息系統的分布約簡和最大分布約簡的具體方法；同時經過例題驗證了此方法的有效性，豐富了區間值模糊序決策信息系統中的粗糙集方法。

2 基于區間值模糊的序決策信息系統

信息決策系統是既有條件屬性又有決策屬性的一種特殊信息系統。信息決策系統主要是研究條件屬性和決策屬性之間的關系問題。為了便于理解，下面給出一些基本概念。

定義1[15]稱一個四元組I=(U,AT?DT,F,G)為一個決策信息系統。其中I=(U,AT,F)是信息系統，AT稱為條件屬性集，DT稱為目標屬性集。

U是有限對象集，U={x1,x2,…,xn}；

AT是有限條件屬性集，AT={a1,a2,…,ap}；

DT是有限決策屬性集，DT={d1,d2,…,dq}；

F是U與AT的關系集，F={f:U→Va,a∈AT}，Va為a的有限值域；

G是U與DT的關系集，G={g:U→Vd,d∈DT}，Vd為d的有限值域。

設I=(U,AT?DT,F,G)為一個決策信息系統，若對任意 f∈F，a∈AT和xi∈U都有：

f(xi,a)=[aL(xi),aU(xi)]

則稱I=(U,AT,F)為區間值模糊信息系統，I=(U,AT?DT,F,G)為區間值模糊決策信息系統。其中aL(xi), aU(xi)∈[0,1]，且aL(xi)≤aU(xi)，f(xi,a)是xi在屬性a下的屬性值范圍（區間數）。特別地，當aL(xi)≡aU(xi)時，f(xi,a)就退化成了一個模糊數。因此區間值模糊信息系統是一般形式，單值模糊信息系統是其特殊形式。

設I=(U,AT,F)為區間值模糊信息系統。對任意的a∈AT，在區間值模糊信息系統中可對屬性值進行比較，定義：

其中“≤”和“≥”可在區間值模糊信息系統中分別構建一個遞增的偏序和一個遞減的偏序。如果區間值模糊信息系統中屬性的值域為遞增的或者遞減的偏序，那么稱該屬性是區間值模糊信息系統中的一個準則。本文只考慮由遞增偏序構成的優勢關系的情景，遞減的偏序情形可以類似地得到相同的結論。

定義2設I=(U,AT?DT,F,G)為區間值模糊決策信息系統，若I中所有條件屬性都是準則，則稱I是區間值模糊序決策信息系統，記作I≥。稱I≥=(U, AT,F)為區間值模糊序信息系統。

在區間值模糊序信息系統中，設a∈AT為準則，存在優勢關系“≥a”，“xj≥axi”表示xj關于準則a優于 xi。設 A?AT是準則集，那么 xj≥Axi?(?a∈A) [xj≥axi]，優勢關系可定義為：

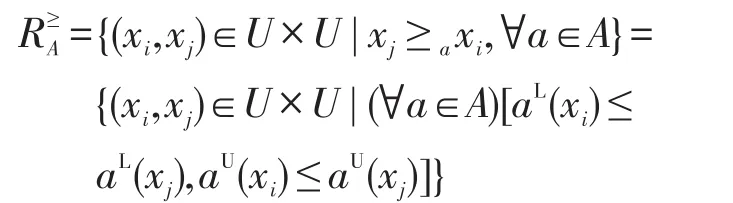
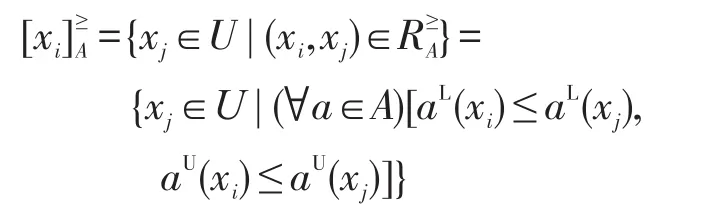
定義3設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統，如果，則稱該區間值模糊序決策信息系統是協調的，否則為不協調的。

本文僅僅考慮不協調區間值模糊序決策信息系統。

3 區間值模糊序信息決策系統的分布約簡

已經知道了序信息系統中屬性約簡理論定義的分布函數和最大分布函數，下面將給出區間值模糊序信息系統中的分布函數和最大分布函數的定義。

定義4設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統。對于任意的A?AT，x∈U，記：

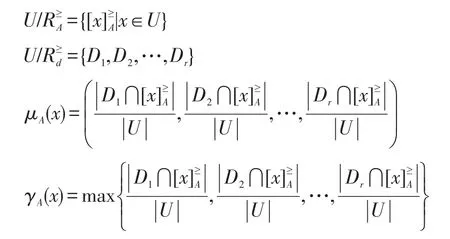
稱 μA(x)為論域U上的關于準則集A和決策d的分布函數，γA(x)為論域U上的關于準則集A和決策d的最大分布函數。

定義5[15]設α=(a1,a2,…,an)和 β=(b1,b2,…,bn)為兩個n維向量，若ai=bi(i=1,2,…,n)，稱向量α等于向量 β，記作α=β；若ai≤bi(i=1,2,…,n)，稱向量α小于等于向量 β，記作α≤β；否則如果存在某個i0(i0∈{1,2,…,n})，使得ai0＞bi0，稱向量α不小于等于向量 β，記作α≮β。

顯然由以上可立即得到下面命題。

定理1設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統。對于任意的A?AT：

（1）對?x∈U，當B?A時，有 μA(x)≤μB(x)；

（2）對?x∈U，當B?A時，有γA(x)≤γB(x)；

定義6設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統。A?AT，對于任意的x∈U，如果有μA(x)=μAT(x)，則稱A是I≥中關于區間值模糊優勢關系的分布協調集；如果A的任何真子集均不是分布協調集，則稱A是I≥中關于區間值模糊優勢關系的分布約簡。

定義7設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統。A?AT，對于任意的x∈U，如果有γA(x)=γAT(x)，則稱A是最大分布協調集；若A的任何真子集均不是最大分布協調集，則稱A是I≥中關于區間值模糊優勢關系的最大分布約簡。

下面具體給出區間值模糊序決策信息系統的分布約簡與最大分布約簡的關系及其判定定理。

定理2設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統，則分布協調集一定是最大分布協調集。

證明 由定義直接可得。 □

推論1設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統，則分布協約簡一定是最大分布約簡。

定理3設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統，A?AT，則A是分布協調集當且僅當對?x,y∈U，當 μAT(y)≮ μAT(x)時有。

證明 反證法。

假設當 μAT(y)≮ μAT(x)時有不成立，則有，由定理1可知 μA(y)≤μA(x)。由于是分布協調集，可得 μAT(x)=μA(x)且 μAT(y)=μA(y)，故有μAT(y)=μAT(x)，與 μAT(y)≮μAT(x)矛盾。 □

用同樣的方法可以得到最大分布協調集的充要條件。

定理4設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統，A?AT是最大分布協調集，則對?x,y∈U，當γAT(y)≮γAT(x)時有。

4 區間值模糊序決策信息系統的分布約簡方法

第3章給出了不協調的區間值模糊序決策信息系統的分布協調集和最大分布協調集的等價刻畫，這是判斷準則集是否協調的理論所在，因此可以得出分布約簡和最大分布約簡的方法。下面給出辨識屬性集以及辨識屬性矩陣的相關概念。

定義8設I≥=(U,AT,F)為區間值模糊序信息系統，記：

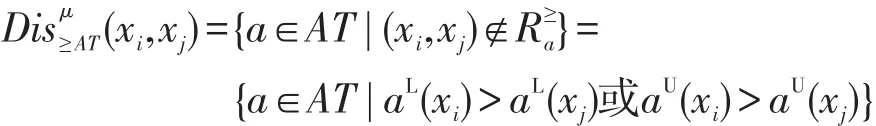
5 實例分析

設I≥=(U,AT?g0gggggg,F,G)為區間值模糊序決策信息系統；U={x1,x2,…,x6}為論域，代表6個投資對象；A={a1,a2,a3}，分別代表著市場風險、技術風險、管理風險；g0gggggg為決策屬性，表示風險，其中3表示“高”，2表示“中”，1表示“低“。統計數據如表1。

Table 1 Interval-valued fuzzy ordered decision information system in venture investment表1 風險投資的區間值模糊序決策信息系統

由表1可得到：

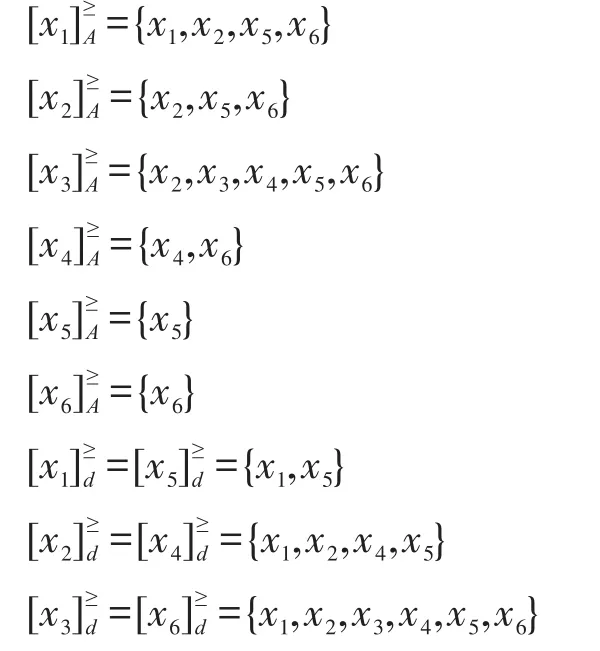
對于表1給出的關于風險投資的區間值模糊序決策信息系統，求分布約簡。

情形1利用定義6、定義7求解。

在該系統中記：

由分布函數 μA(x)及其最大分布函數γA(x)定義可得：

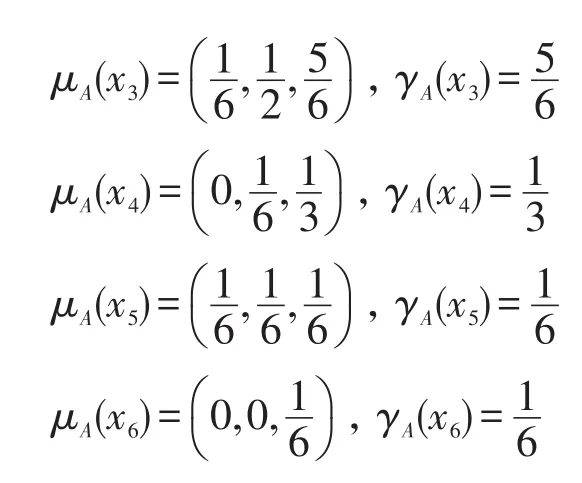
當取 B={a2,a3}時，容易驗證對于?x∈U，有，因此有 μB(x)=μA(x)和 γB(x)=γA(x)。故B={a2,a3}是個分布協調集，也是個最大分布協調集。進一步可以計算{a2}、{a3}均不是分布協調集和最大分布協調集，因此B={a2,a3}是分布約簡，是一個最大分布約簡。

容易驗證{a1,a3}、{a1,a2}和{a1}都不是分布協調集，也不是最大分布協調集，因此該區間值模糊決策信息系統只有一個分布約簡，也只有一個最大分布約簡，即{a2,a3}。

情形2利用定理5求解。

該信息系統的分布辨識矩陣如表2所示。

Table 2 Distribution discernibility matrix of intervalvalued fuzzy ordered decision information system表2 區間值模糊序決策信息系統的分布辨識矩陣

由定義9可得：

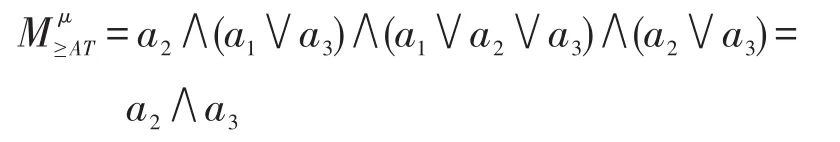
因此{a2,a3}是該區間值模糊序決策信息系統的所有分布約簡，而且也是最大分布約簡。

這里針對情形2提出如下算法：

算法 區間值模糊序決策信息系統分布約簡

輸入：區間值模糊序決策信息系統I≥=(U,AT?g0gggggg,F,G)

輸出：分布約簡

算法的時間復雜度如表3所示。

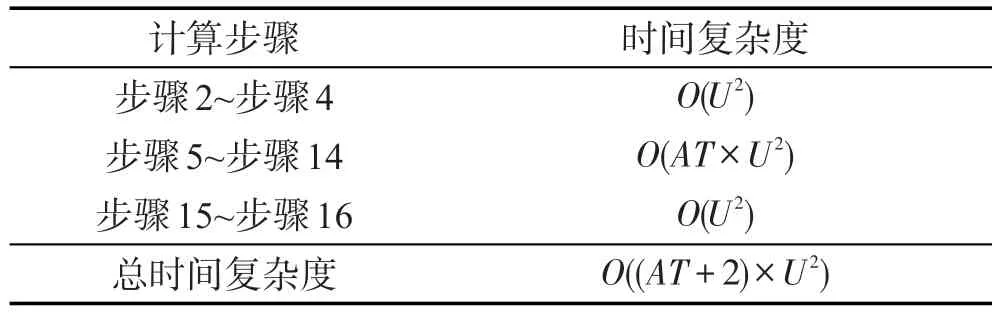
Table 3 Time complexity on case 2表3 情形2算法的時間復雜度

上述情形1和情形2所求得的結果是一致的，顯然在該決策問題中技術和管理風險因子是不可缺少的，但是其時間復雜性不一樣。情形1從定義出發，時間復雜度較高，不太具有可行性；而情形2的時間復雜度為O((AT+2)×U2)。在這個例子中體現了求分布約簡時，利用情形2求解具有明顯的時間優勢。

6 結束語

本文在不協調的區間值模糊序決策信息系統中通過分析分布約簡的性質得到了對應的判定定理以及辨識矩陣，建立了獲取這種約簡的具體方法，并且用兩種情形對實例進行了對比分析。通過比較可以知道，本文對分布約簡進行了更精確的刻畫，可以簡化在時間上的求解過程。

[1]Pawlak Z.Rough sets:theoretical aspects of reasoning about data[M].Boston:KluwerAcademic Publishers,1991.

[2]Pawlak Z,Grzymalabusse J,Slowinski R,et al.Rough sets [J].Communication of theACM,1995,38(11):88-95.

[3]Wang Yu,Miao Duoqian,Zhou Yujian.A summary of the theory and application on rough set[J].Pattern Recognition andArtificial Intelligence,1996,9(4):337-344.

[4]Miao Duoqian,Wang Yu.Rough sets based approach for multivariate decision tree construction[J].Journal of Software,1997,8(6):425-431.

[5]Zhang Xiaohong,Pei Daowu,Dai Jianhua.Fuzzy mathematics and the rough set theory[M].Beijing:Tsinghua University Press,2013.

[6]Xu Weihua,Zhang Xiantao,Wang Qiaorong.Experimental computing on attribute by Matlab in dominance-based variable precision rough set[J].Journal of Chongqing University of Technology,2013,27(1):107-115.

[7]Xu Weihua,Zhang Wenxiu.Knowledge reductions in inconsistent information systems based on dominance relations [J].Computer Science,2006,33(2):182-184.

[8]Mi Jusheng,Wu Weizhi,Zhang Wenxiu.Comparative studies of knowledge reductions in inconsistent systems[J].Fuzzy Systems and Mathematics,2003,17(3):54-60.

[9]Zhang Wenxiu,Mi Jusheng,Wu Weizhi.Knowledge reductions in inconsistent informaion systems[J].Chinese Journal of Computers,2003,26(1):12-18.

[10]Zhang Wenxiu,Liang Yi,Wu Weizhi.Information system and knowledge discovery[M].Beijing:Science Press,2003.

[11]Yu Yiingying,Zeng Xuelan,Sun Xingxing.Interval-valued information systems based on dominance relation and its attribute reduction[J].Computer Engineering and Applications,2011,47(35):122-124.

[12]Zhang Nan,Miao Duoqian,Yue Xiaodong.Approaches to knowledge reduction in interval-valued information system[J].Computer Research and Development,2010,47(8): 1362-1371.

[13]Greco S,Matarazzo B,Slowinski R.Rough approximation of a preference relation by dominance relations[J].European Journal of Operational Research,1999,117(1):63-68.

[14]Xu Weihua,Zhang Wenxiu.Consistent approximation spaces based on dominance relations[J].Computer Science,2005, 32(9):164-165.

[15]Xu Weihua.Ordered information systems and rough sets theory[M].Beijing:Science Press,2013.

[16]Yu Jianhang,Xu Weihua.Rough set based on logical disjunct operation of variable precision and grade in ordered information system[J].Journal of Frontiers of Computer Science and Technology,2015,9(1):112-118.

[17]Sun Wenxin,Zhuo Chunying,Wang Guodong,et al.Generalized multi-granulation rough set in ordered information system[J].Journal of Frontiers of Computer Science and Technology,2015,9(3):376-384.

[18]Xu Weihua,Zhang Wenxiu.Distribution reduction in inconsistent information systems based on dominance relations[J]. Fuzzy Systems and Mathematics,2007,21(4):124-131.

附中文參考文獻：

[5]張小紅,裴道武,代建華.模糊數學與Rough集理論[M].北京:清華大學出版社,2013.

[9]張文修,米據生,吳偉志.不協調目標信息系統的知識約簡[J].計算機學報,2003,26(1):12-18.

[10]張文修,梁怡,吳偉志.信息系統與知識發現[M].北京:科學出版社,2003.

[15]徐偉華.序信息系統與粗糙集[M].北京:科學出版社, 2013.

[16]余建航,徐偉華.序信息系統下變精度與程度的“邏輯或”粗糙集[J].計算機科學與探索,2015,9(1):112-118.

[17]孫文鑫,卓春英,王國棟,等.序信息系統的一般多粒度粗糙集[J].計算機科學與探索,2015,9(3):376-384.

SHI Derong was born in 1991.She is an M.S.candidate at Chongqing University of Technology.Her research interest is the mathematical foundation of artificial intelligence.

史德容（1991—），女，重慶人，重慶理工大學碩士研究生，主要研究領域為人工智能的數學基礎。

XU Weihua was born in 1979.He received the Ph.D.degree from Xi’an Jiaotong University in 2007.Now he is the vice-dean,professor and M.S.supervisor at School of Sciences,Chongqing University of Technology,and the director of Chongqing Mathematical Society.His research interests include artificial intelligence,granular computing,fuzzy mathematics and rough set,etc.

徐偉華（1979—），男，山西渾源人，2007年于西安交通大學獲得博士學位，現為重慶理工大學理學院副院長、教授、碩士生導師，主要研究領域為人工智能，粒計算，模糊數學，粗糙集等。

Distribution Reduction in Interval-Valued Fuzzy Decision Ordered Information Systems*

SHI Derong,XU Weihua+
School of Sciences,Chongqing University of Technology,Chongqing 400054,China
+Corresponding author:E-mail:chcuwh@gmail.com

Because of the complexity and uncertainty of information systems,it's hard to use accurate value to represent the object's attribute value.The interval-value which blurred is used to deal with the issue.This paper introduces dominance relations to establish inconsistent interval-valued fuzzy ordered decision information system.Then,this paper considers distribution reduction and maximum distribution reduction to simplify the expression of knowledge, at the same time,finds out the relationship between them.Moreover,this paper obtains judgment theorem of distribution reduction and maximum distribution reduction and discernibility matrix in the system.It also provides specific method of distribution reduction and maximum distribution reduction in interval-valued fuzzy ordered decision information system.Furthermore,this paper analyzes a specific case about the venture investment and discusses the significance of study on distribution reduction.Finally,this experiment enriches rough set method for interval-valued fuzzy ordered decision information system.

rough set;interval-value;ordered information system;distribution reduction

10.3778/j.issn.1673-9418.1602002

A

TP18

*The National Natural Science Foundation of China under Grant Nos.61105041,61472463,61402064(國家自然科學基金);the Natural Science Foundation of Chongqing under Grant No.cstc2015jcyjA1390(重慶市自然科學基金);the Graduate Innovation Foundation of Chongqing under Grant No.CYS16217(重慶市研究生創新基金);the Graduate Innovation Foundation of Chongqing University of Technology under Grant Nos.YCX2015227,YCX2016227(重慶理工大學研究生創新基金).

Received 2016-02,Accepted 2016-06.

CNKI網絡優先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1144.002.html

SHI Derong,XU Weihua.Distribution reduction in interval-valued fuzzy decision ordered information systems.Journal of Frontiers of Computer Science and Technology,2017,11(4)：652-658.

摘 要：因信息系統的復雜性和不確定性，對象的屬性值難以用精確的數值來表達，而是采用區間形式表示。針對這一問題，對區間值進一步模糊化，并引進優勢關系，建立了不協調區間值模糊序決策信息系統。通過分布約簡和最大分布約簡來簡化知識的表達，找出二者之間的關系，得到了分布約簡和最大分布約簡的判定定理以及可辨識屬性集和可辨識矩陣；提供了不協調的區間值模糊序信息系統的分布約簡和最大分布約簡的具體方法；結合投資風險這一具體案例的求解分析，進一步闡述了對分布約簡研究的意義，豐富了區間值模糊序決策信息系統中的粗糙集方法。