車輛整備狀態車體垂彎頻率優化方法研究

尤泰文， 周勁松， 任利惠, 宮 島

(同濟大學 鐵道與城市軌道交通研究院，上海 201804)

車輛整備狀態車體垂彎頻率優化方法研究

尤泰文， 周勁松， 任利惠, 宮 島

(同濟大學 鐵道與城市軌道交通研究院，上海 201804)

為提高軌道車輛整備狀態車體垂向一階彎曲頻率，提出基于靈敏度分析和車下設備彈性吊掛參數設計方法優化車體垂向一階彎曲頻率。以車身型材骨架厚度為設計變量，用模態靈敏度理論對車體垂彎進行優化設計；結合改進車下設備與車體連接方式，研究了不同吊掛形式及剛度對車體垂向彎曲頻率的影響。研究結果表明：采用靈敏度分析調整車體敏感部件厚度后，車體垂向一階彎曲頻率由9.70 Hz提升至10.60 Hz，但車體質量相應增加0.93 t；而采用基于車下設備彈性吊掛參數設計的方法，設置下吊設備固有頻率為7 Hz時，整備狀態車體的垂向一階彎曲模態頻率提升至10.51 Hz，相對而言基于彈性吊掛參數設計的方法更易于實際工程應用且不增加車體結構質量。

軌道車輛；整備狀態；垂彎頻率；靈敏度分析；彈性吊掛

目前軌道車輛車體廣泛采用輕量化設計，在降低車體承載結構質量同時也帶來了車體剛度下降的問題，在進行輕量化的同時保證車體具有較高的垂彎頻率成為目前國內外專家學者研究的熱點。李永樂等[1-3]建立了高速車輛輕量化前后的有限元模型，對比分析了輕量化對車體模態頻率的影響，結果表明輕量化后車體各階模態頻率均出現了不同程度地下降；郭祥濤[4]采用靈敏度分析法進行車體輕量化同時使車體靜強度得到了提高；鄔廣銘等[5]將靈敏度分析法用于汽車設計，研究了靈敏度分析法在優化汽車車身模態頻率上的應用，提高了白車身前兩階固有頻率；宮島等[6]研究了車下設備對整備狀態車體模態頻率的影響，結果表明不同的車下設備布置方式對模態頻率均有影響，且提出了車下設備和車體模態頻率的匹配方法。以上基于靈敏度分析只研究了軌道車輛車體輕量化、強度優化計算及汽車模態頻率優化。目前，提高車輛垂向彎曲頻率常采用優化車身拓撲結構、調整車輛設備分布、使用新型材料等方法，這些方法實際應用繁瑣且效果有限，難以達到預期目的。

基于此，本文以國內某型軌道車輛為研究對象，在前期研究基礎上提出基于靈敏度分析與下吊設備懸掛參數設計兩種車體垂彎頻率優化方案。通過計算與試驗，對比分析以上兩種方法對車體一階垂彎頻率的優化效果及各自優缺點，提出可廣泛應用于軌道車輛整備狀態車體垂彎頻率的優化方法。

1 整備狀態車體有限元模型建立與模態分析

1.1 有限元模型

本文所研究的軌道車輛車體為整體承載無中梁筒形結構，由端墻、側墻、底架、車頂和裙板五大部分組成。首先建立車體的有限元模型，車身采用四節點的板單元進行離散，車下設備包括電空制動裝置、充電器、逆變器、蓄電池和污物箱等，設置這些設備剛性連接于吊掛梁或吊腳處，下吊設備及內飾采用MASS單元模擬。完整的軌道車輛整備狀態下車體有限元模型如圖1所示。

圖1 車體有限元模型

該車體模型共包含2 650 181個單元，813 117個節點，車體材料為低碳鋼，其具體參數如表1所示。下吊設備的吊掛方式以電空制動裝置為例，剛性連接如圖2所示。

表1 車體材料參數

圖2 車下設備剛性連接

1.2 計算模態與試驗模態對比分析

對車體有限元模型進行整備狀態模態分析，計算了其在0～200 Hz范圍內的模態，提取了主要振型的模態頻率結果如表2所示，計算得到車體的一階垂向彎曲頻率為9.22 Hz。

為了檢驗有限元建模與計算的準確性，對該車進行模態測試用于檢驗及修正有限元模型。使用掃頻激勵信號激勵車體，記錄振動加速度響應信號，本次試驗采用的是垂向沖擊激勵。通過對激勵點進行激勵，獲得車體模態頻率。實車測試時，被試車體采用橡膠彈簧支撐，采用加速度傳感器采集信號，測點布置位置如圖3所示。

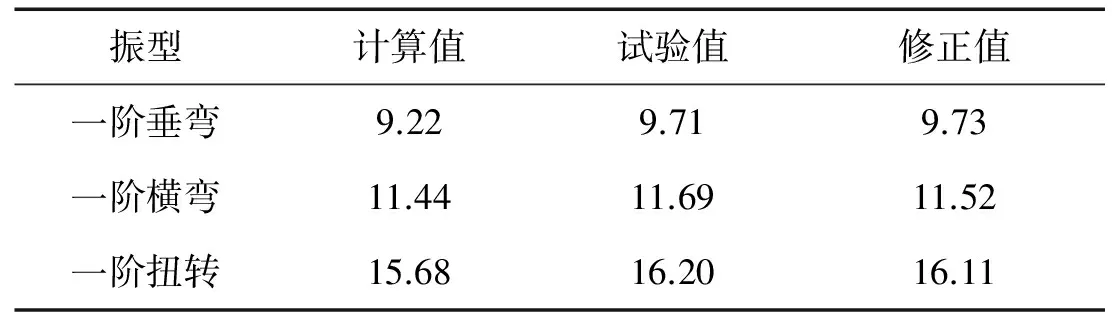
表2 模態頻率結果及修正

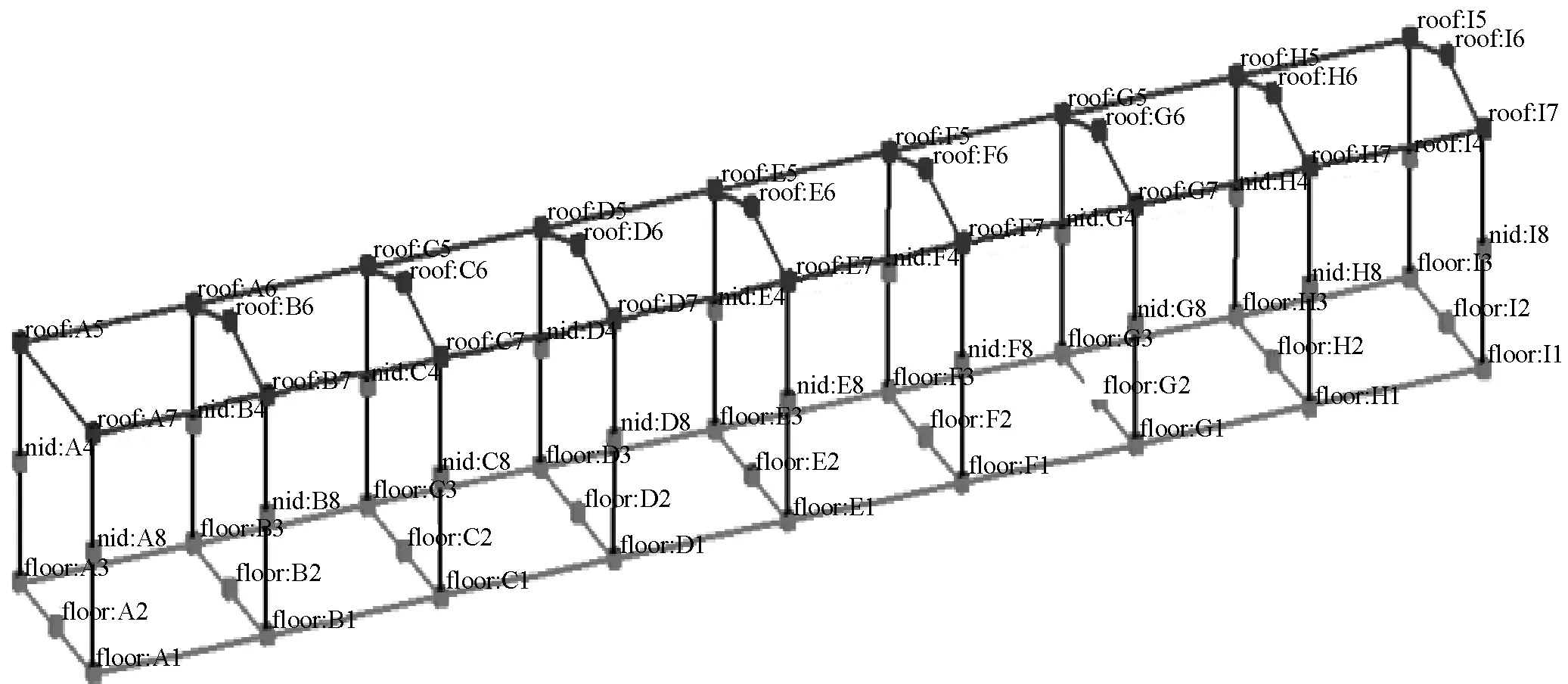
圖3 車體模態試驗測點

試驗結果見表2。有限元計算結果與模態測試結果存在一定的誤差，這是由于有限元建模過程中，忽略了車體上個別無法準確模擬的部件，如：車體內裝、行李架等，這些部件較為均勻分布在車內，對車體的整體剛度有一定影響。因此，采用當量彈性模量法對初始有限元模型進行修正[7]，將彈性模量增加10%，其結果列于表2，修正后計算結果與試驗結果基本一致(最大誤差0.5%)。

由于該車體垂向一階彎曲頻率低于10 Hz，不滿足軌道車輛動力學標準的相關規定。為此，針對本文研究的軌道車輛車體，進一步進行優化研究。

2 基于靈敏度分析優化車體垂彎頻率

2.1 模態靈敏度理論

設ωi及ui分別為車身結構第i階模態固有頻率與振型向量，滿足：

(1)

式中:K為結構模型總剛度矩陣;M為結構模型總質量矩陣，其維數即為結構模型自由度數。

對式(1)求導得到：

(2)

式中:ωi,j為ωi對設計變量b(板厚)的偏導數；ui,j為ui對設計變量b(板厚)的偏導數；Kj為K對設計變量b(板厚)的偏導數；Mj為對設計變量b(板厚)的偏導數，j為第j階導數。

其中：

(3)

在有限元中，K及M分別為單元剛度矩陣以及單元質量矩陣Me的求和，即：

式(4)、(5)對參數b求導,有：

(6)

(7)

式(3)可轉化為

(8)

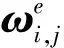
2.2 靈敏度優化分析

車體的質量取決于車體材料及車體結構，采用靈敏度分析法優化車體結構進而改善車體剛度[9]。優化以車體垂彎頻率的提高為目的，設置車體整備狀態一階垂彎模態頻率為優化目標，以車身質量增幅小于5%為約束條件，分析各部件厚度對車體一階垂彎模態頻率的靈敏度，最終得到各部件厚度的最優解。

對軌道車輛而言，通常車體剛度主要由車體承載結構提供，為避免優化過程中改變其它振型模態頻率，使設計變量對設計目標一階垂彎頻率有顯著效果，選取車體承載結構的18個主要支撐骨架厚度為設計變量，優化的各部件如圖4所示。

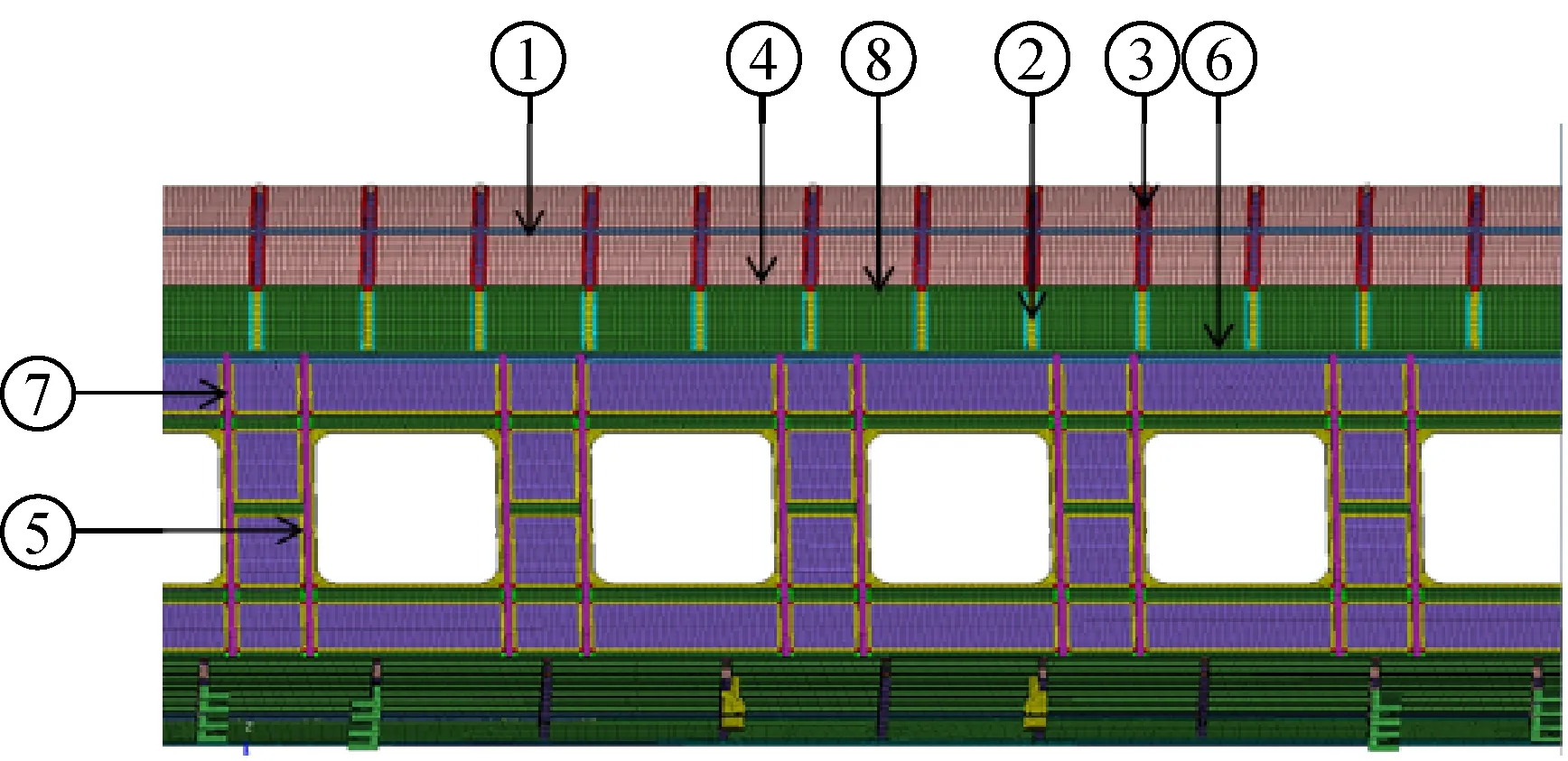
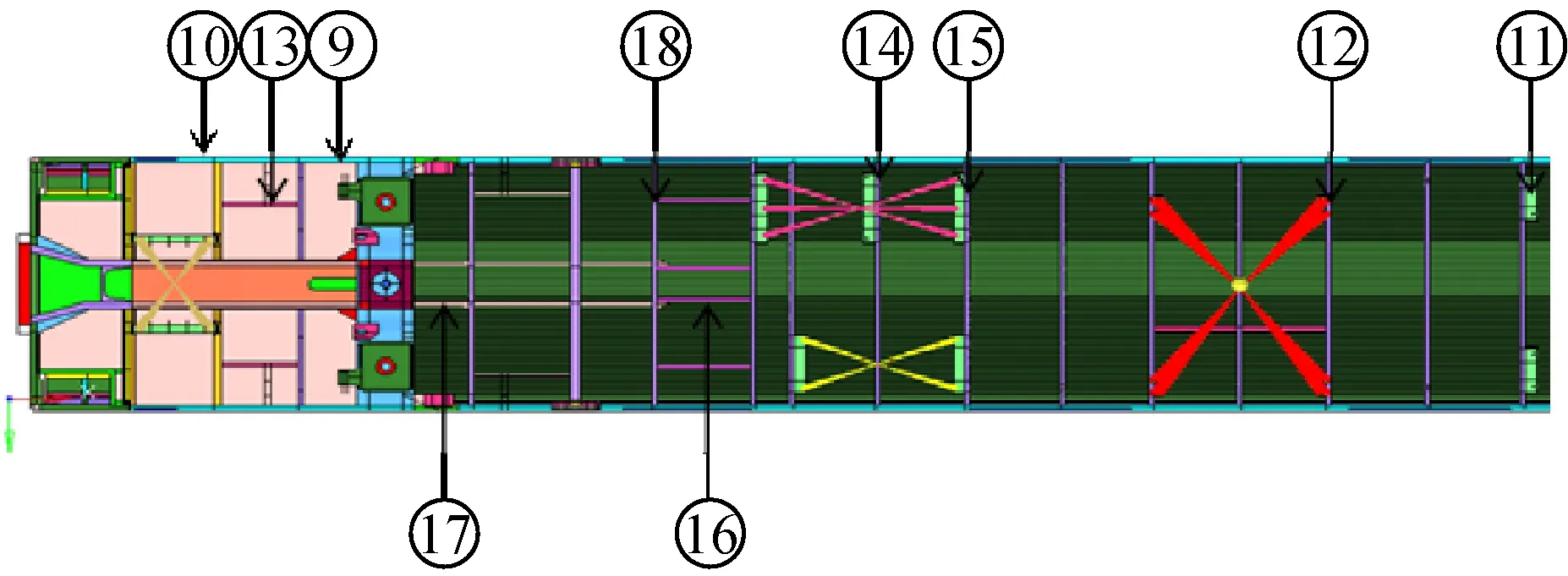
圖4 靈敏度優化部件

在優化過程中，初始值為各部件的原始厚度，分別計算了各部件厚度對垂彎頻率和車體質量的靈敏度，優化所選設計變量及分析結果如表3所示。

研究表明，靈敏度分析時車體垂彎頻率與車體質量會同時提高[10]為避免質量增加對頻率的影響保證一階垂彎頻率提高時質量增幅最小，確保車體結構的輕量化，構造新指標來衡量整個構件質量變化對一階垂彎頻率靈敏度的影響，定義相對靈敏度S為

(9)

式中：F為一階垂彎頻率對構件厚度的靈敏度；M為質量對構件厚度的靈敏度。依據上述公式計算得到一階垂彎頻率對車體可調整構件的相對靈敏度結果，如表4所示。

表4中靈敏度值為正表示增加厚度有助于垂彎頻率的提高且質量增加最少，靈敏度值為負表示增加厚度會降低一階垂彎頻率同時質量會提升，靈敏度值趨近零值表示該部件厚度變化對于一階垂彎頻率的影響較小。表中，相對靈敏度最高的部件為18號橫梁，表面增加橫梁厚度對于提高一階垂彎頻率最敏感，其次為13號吊梁，9號、10號邊梁。

在優化變量部件允許設計變更的范圍內，取相對靈敏度較大的4個構件進行厚度尺寸優化。優化后進行模態分析，結果如表5所示。

對車體結構部件的料厚尺寸優化后，在質量增加2.3%的情況下，垂彎頻率提升9.3%至10.60 Hz，其它振型頻率未見明顯變化。但是該方法在提高一階垂彎頻率的同時，車體本身的自重也在增加，會導致簧上質量增大，這與車體的輕量化設計原則相違背。因而，研究提出一種提高車體一階垂彎頻率而不改變或者降低車體質量的方法更為重要。

表3 靈敏度分析結果

表4 相對靈敏度分析結果

3 基于吊掛參數設計優化車體垂彎頻率

整備狀態車體由車體承載結構、車輛內裝、車下設備以及各連接件組成，其系統振動包含結構的剛體和彈性體振動，是一個剛柔耦合振動系統[12]。為了研究車體與設備間的振動關系，建立車體與吊掛設備的兩自由度垂向模型，如圖5所示。由于車體結構的模態阻尼比一般在0.015～0.05之間[13]，其對車體固有頻率的影響很小，故在該模型中忽略阻尼的影響。

表5 靈敏度優化分析結果

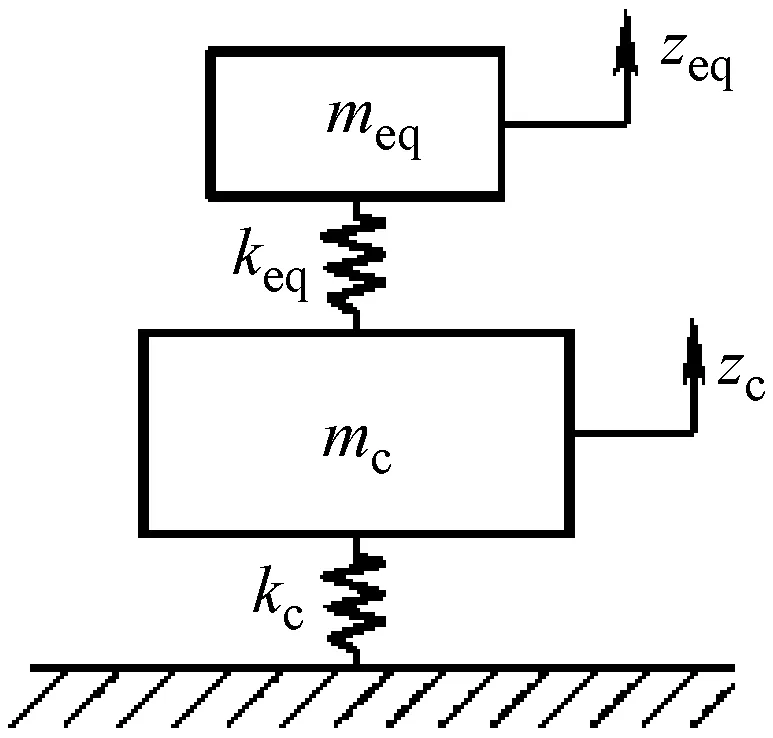
圖5 車體及車下設備兩自由度模型

圖5中，meq為車下設備質量，keq為車下設備吊掛剛度，mc為車體質量；kc為車體彎曲剛度，由于車體彎曲剛度主要由承載結構提供，其余附件對彎曲剛度影響較小，因而針對車體垂向一階彎曲模態，kc可以表示為

(10)

式中：ms為車體承載結構質量；ωs1為車體承載結構垂向一階彎曲模態頻率。

根據圖5等效模型，可以得到耦合系統振動頻率解為

ω1=

(11)

ω2=

(12)

由式(11)、(12)可知，當車下設備采用彈性吊掛時，設備與車體構成耦合系統，此時，車體與車下設備的振動分別由低頻ω1與高頻ω2兩種頻率振動波疊加而成，即：

(13)

式中:A1與B1分別為車體和設備在低頻時振動波的幅值；A2與B2分別為車體和設備在高頻時振動波的幅值。

實際設計中通常通過車下設備吊掛元件靜撓度來描述吊掛元件，車下設備吊掛靜撓度x與吊掛剛度之間關系可用下式描述：

(14)

采用靜撓度來描述車下設備吊掛剛度的變化，將車體參數代入，得到系統低頻與高頻振動頻率隨靜撓度的變化結果如圖6所示。圖中實線代表低頻振動，虛線代表高頻振動。

圖6中，車體與設備為剛性連接時(靜撓度為0 mm)，系統表現為單自由度系統，振動頻率為9.70 Hz；隨著吊掛結構靜撓度逐漸增大，低頻振動頻率逐漸降低，高頻振動頻率急劇下降，車體垂彎頻率從低頻振動轉向高頻振動，車體與設備之間由剛性連接轉向彈性連接，從單自由度系統向兩自由度系統轉變。

隨靜撓度繼續增大，車體與設備之間連接剛度逐漸降低，兩自由度系統向只有車體的單自由度系統轉變，低頻振動頻率向0 Hz趨近，垂彎振動頻率趨近于無下吊時整備狀態車體垂向一階彎曲頻率10.97 Hz。因此，采用彈性吊掛方式可以提高車體垂彎頻率，本節以車下設備的吊掛方式及吊掛參數作為研究對象，研究提高車體垂彎頻率的方法。

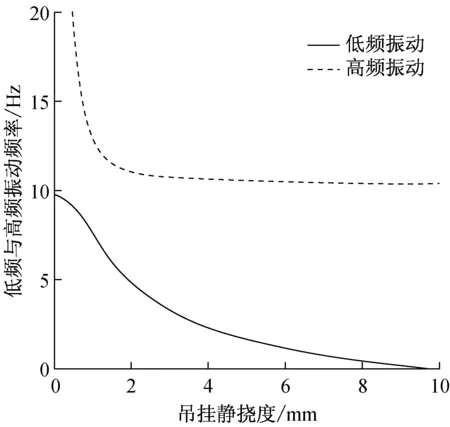
圖6 振動頻率隨吊掛靜撓度變化

本文選用橡膠作為彈性隔振元件，采用三維彈性單元模擬橡膠元件，在上述剛性吊掛處，用彈性單元代替剛性連接單元[14]。彈性單元的剛度由下式可得：

(15)

式中:keq為設備吊掛剛度;feq為設備吊掛頻率;kd為彈性元件的動剛度值，隨著環境溫度、振動頻率、橡膠材料變化而變化，取值一般在1.2～2.8，本文選取1.4[15]。圖7所示為車下設備采用彈性吊掛時的有限元局部模型。結合隔振設計理論[15]，將設備的吊掛頻率設定為6 Hz、7 Hz、8 Hz和9 Hz，分析車體整備狀態下低階典型模態振型及其對應的頻率值。表6為采用不同吊掛參數時車體彈性模態的計算結果。

圖7 車下設備彈性連接

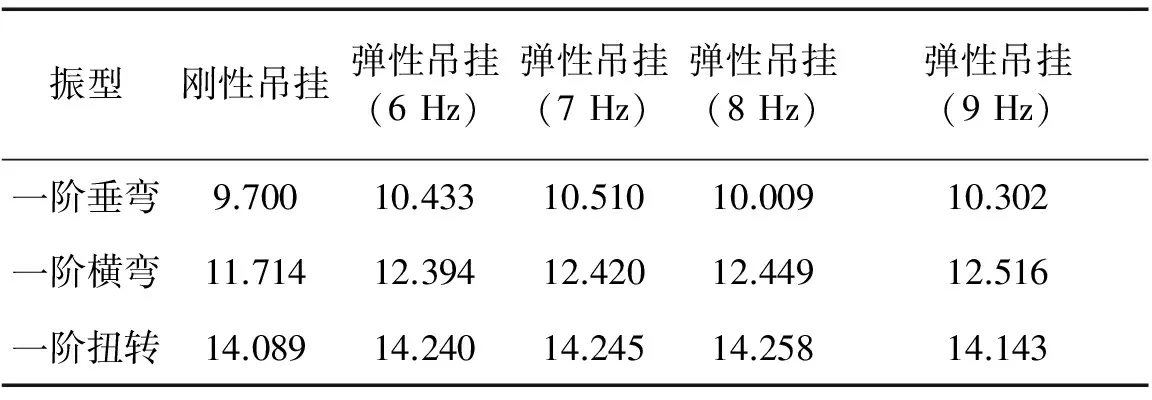
表6 彈性吊掛車體模態頻率結果

由表6可知，將車下設備與車體的連接方式由剛性變為彈性，大部分低階車體模態振型的頻率有不同程度的提高，且不增加車體重量。設備獨立吊掛頻率取為6 Hz、7 Hz和9 Hz時，一階垂彎頻率的提高較為明顯。一般車體一階垂彎頻率在10 Hz左右，若設備頻率選取9 Hz易發生共振，影響車輛運行平穩性[16]。因而，優先考慮設計吊掛頻率為6 Hz與7 Hz。同時，下吊設備的吊掛頻率并不是與車體垂彎頻率正相關的，而是在吊掛頻率為6 Hz、7 Hz時呈現車體垂彎頻率上升，至8 Hz時垂彎頻率下降的趨勢。

值得注意的是，轉向架浮沉頻率一般在5～8 Hz范圍，但由于車體一系、二系減振器的作用，轉向架浮沉振型阻尼比較大[17]，其自振頻率范圍的振動將明顯衰減，軌道不平順激擾經轉向架兩系懸掛傳遞至車體的振動主要集中于2 Hz以下[18]，因此車下設備在該頻段內振動能量得到很大程度的抑制。

上述分析表明使用優化車下設備吊掛的方式可以提高整備狀態車體垂彎頻率，相較于靈敏度分析易于實現，不改變車體質量。

4 結論

(1)本文提出優化整備狀態車體垂彎頻率的兩種方法：將靈敏度分析運用到車體垂彎頻率優化，通過改進車體剛度與車體質量達到優化頻率目的；吊掛方式優化通過改變車體和設備的耦合振動方式，從而使得該型車輛滿足相關車體彈性模態頻率標準要求。

(2)用模態靈敏度理論對整備狀態車體進行靈敏度分析。根據最優方案和模態分析結果表明：優化后車體垂向一階彎曲頻率提升9.2%，但車體質量增加了2.35%。靈敏度分析可提高車體垂向一階彎曲頻率，但由于質量的增加可能會導致其它模態頻率惡化，需進一步研究。

(3)從設備吊掛方式入手，改變設備與車體底架之間的連接方式，減少設備與車體的耦合振動。合理設置車下設備的連接方式和隔振懸掛參數可有效改善車體垂向一階彎曲頻率。根據本文方案當設備的吊掛頻率設計為7 Hz時，車體垂向一階彎曲頻率提升至10.51 Hz，同時車體質量增加亦不明顯。

[1] 李永樂，周樂家，李曉燕. 高速列車鋼質拖車車體輕量化設計研究[J].鐵道車輛，2002，40(6)：13-21.

LI Yongle, ZHOU Lejia, LI Xiaoyan. Lightening design and research on steel trailer car bodies of high speed trains[J]. Rolling Stock, 2002,40(6):13-21.

[2] 沈宏峻，周勁松，薛向東，等. 鉸接式客車車體的輕量化設計和模態分析[J].鐵道學報，1997(19):46-51.

SHEN Hongjun, ZHOU Jinsong, XUE Xiangdong, et al. Optimized lightening design and modal analysis of articulated car body[J]. Journal of the China Railway Society, 1997(19):46-51.

[3] 姚曙光，田紅旗，許平. 重載敞車車體結構輕量化設計[J]. 交通運輸工程學報，2011，11(1): 31-35.

YAO Shuguang, TIAN Hongqi, XU Ping. Lightening design of carbody structure for heavy haul gondola[J]. Journal of Traffic and Transportation Engineering, 2011,11(1):31-35.

[4] 郭祥濤. 高速動車組鋁合金車體結構分析及基于靈敏度分析的優化[D]. 北京：北京交通大學，2011.

[5] 鄔廣銘，史文庫，劉偉，等. 基于模態靈敏度分析的客車車身優化[J]. 振動與沖擊，2013，32(3)：41-45.

WU Guangming, SHI Wenku, LIU Wei, et al. Structural optimization of a light bus body-in-white based on modal sensitivity analysis[J]. Journal of Vibration and Shock, 2013,32(3):41-45.

[6] 宮島，周勁松，孫文靜，等. 高速列車車下設備模態匹配研究[J]. 振動與沖擊，2014，33(8)：180-185.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Modes matching between suspended devices and carbody for a high speed rail way vehicle[J]. Journal of Vibration and Shock, 2014,33(8):180-185.

[7] 宮島，周勁松，孫文靜，等. 高速列車車下設備模態匹配及試驗研究[J]. 鐵道學報，2014，36(10): 13-20.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Modal matching between suspended equipment and car body of a high-speed railway vehicle and in-situ experiment[J]. Journal of the China Railway Society, 2014,36(10):13-20.

[8] KODIYALAM S, YANG R J, GU L, et al. Multidisciplinary design optimization of a vehicle system in a scalable, high performance computing environment[J]. Structural and Multidisciplinary Optimization, 2004,26(3):256-263.

[9] 謝素明，閆雪冬，兆文忠. 基于敏度信息的鋁型材高速車體輕量化研究[J]. 鐵道學報，2004，26(3): 26-30.

XIE Suming, YAN Xuedong, ZHAO Wenzhong. Research on weight lightening of the high-speed aluminum-profile car body based on sensitivity information[J]. Journal of the China Railway Society, 2004,26(3): 26-30.

[10] 丁莉芬，繆龍秀. 基于靈敏度分析的結構動力修改方法研究[J]. 鐵道學報，1999，21(4): 18-20.

DING Lifen, MIAO Longxiu. Study of structural dynamics modification based on sensitivity analysis[J]. Journal of the China Railway Society, 1999,21(4):18-20.

[11] 陸正剛，郭慧明. 柔性車體振動和運行平穩性控制研究[J].中國機械工程，2006，17(10):416-420.

LU Zhenggang,GUO Huiming.Flexible vehicle vibration active control and ride quality improvement[J].China Mechanical Engineering,2006,17(10):416-420.

[12] NETTER H. New aspects of contact modeling and validation within multibody system simulation of railway vehicle[J]. Vehicle System Dynamics,1997,29(1):246-269.

[13] 黃彩虹，曾京，鄔平波，等. 鐵道客車車體彈性振動減振研究[J]. 工程力學, 2010,27(12): 250-256.

HUANG Caihong, ZENG Jing, WU Pingbo,et al. Study on carbody flexible vibration reduction for railway passenger carriage[J]. Engineering Mechanics, 2010,27(12): 250-256.

[14] 徐鳳妹，勞世定. 客車車下設備吊掛方式的研究[J]. 鐵道車輛，2009，47(4): 12-14.

XU Fengmei, LAO Shiding. Research on the hanging mode of equipment under passenger cars[J]. Rolling Stock, 2009, 47(4): 12-14.

[15] 高陽，孫玲玲，王曉樂. 考慮設備彈性的隔振系統[J]. 噪聲與振動控制，2014，34(4):138-147

GAO Yang, SUN Lingling, WANG Xiaole. Isolation effect of the system with equipment support’s flexibility[J]. Noise and Vibration Control, 2014,34(4):138-147.

[16] 宮島，周勁松，孫文靜，等. 高速列車彈性車體與轉向架耦合振動分析[J]. 交通運輸工程學報，2011，11(4): 41-47.

GONG Dao, ZHOU Jinsong, SUN Wenjing. Analysis on the coupled vibration between flexible car body and bogies of high speed railway vehicles[J]. Journal of Traffic and Transportation Engineering, 2011, 11(4):41-47.

[17] 周勁松，宮島，孫文靜,等. 鐵道客車車體垂向彈性對運行平穩性的影響[J]. 鐵道學報, 2009，31(2)：32-37.

ZHOU Jinsong, GONG Dao, SUN Wenjing, et al. Influence of vehicles elasticity of car body of railway passenger vehicles in ride quality[J]. Journal of the China Railway Society, 2009，31(2)：32-37.

[18] 任尊松，劉志明. 高速動車組振動傳遞及頻率分布規律[J]. 機械工程學報, 2013，49(16)：1-7.

REN Zunsong，LIU Zhiming. Vibration and frequency domain characteristics of high speed EMU[J]. Journal of Mechanical Engineering，2013，49(16)：1-7.

Optimal design of modal frequencies for railway vehicle car-bodies

YOU Taiwen, ZHOU Jinsong, REN Lihui, GONG Dao

(Institute of Rail and Transit, Tongji University, Shanghai 201804, China)

The sensitivity analysis and design of flexible suspension parameters of hanging devices were proposed to improve the first order vertical bending frequency of the fully equipped car bodies. The vertical bending frequency was optimally designed with the thickness of body frame as design variables based on the modal sensitivity analysis theory. The influence of suspended forms and rigidity of rubber on the first vertical bending frequency was analyzed. The results show that the first vertical bending frequency of the car body can be changed from 9.70 Hz to 10.60 Hz while the mass of car body was increased by 0.93 t. The first vertical bending frequency of FE models of fully equipped car bodies was enhanced to 10.51 Hz by adopting the method of flexible suspension while the mass of the car body was constant. In contrast with the sensitivity analysis, the design of flexible suspension parameters of hanging devices is easier for engineering application and the mass of car body is constant.

railway vehicle; severing condition; bending modal frequency; sensitivity analysis; flexible suspension parameter

“十二五”國家科技支撐計劃項目(2015BAG19B02)

2015-11-11 修改稿收到日期：2016-04-11

尤泰文 男,博士生,1992年生

周勁松 男，博士，教授，博士生導師，1969年生

U270.1

A

10.13465/j.cnki.jvs.2017.08.014