基于最佳一致光滑逼近的孿生支持向量機研究

唐輝軍 白 玲 楊志民

1(寧波大紅鷹學院信息工程學院 浙江 寧波 315175)2(浙江工業大學之江學院理學院 浙江 杭州 310023)

基于最佳一致光滑逼近的孿生支持向量機研究

唐輝軍1白 玲1楊志民2

1(寧波大紅鷹學院信息工程學院 浙江 寧波 315175)2(浙江工業大學之江學院理學院 浙江 杭州 310023)

孿生支持向量機本質為兩個二次規劃問題，對于其目標函數中約束變量取正號不可微特性，提出一種基于最佳一致逼近的多項式光滑函數構建方法。分別以Bernstain多項式和Chebyshev多項式進行正號函數最佳一致有效光滑逼近。重點突出Chebyshev多項式的最佳一致逼近過程，使用Remez算法構造最佳一致Chebyshev多項式，討論各階Chebyshev多項式逼近狀況。最后綜合最佳一致逼近多項式和樣本適應度構建目標優化函數，采用快速Newton-Armijo算法求解目標優化函數，基于UCI數據驗證了方法的優越性。

孿生支持向量機 最佳一致逼近 適應度

0 引 言

支持向量機[1](SVM)被認為是能較好地對多角色個體進行有效分類和回歸的重要工具。可在不同應用領域針對小樣本、非線性模式識別表現出獨特的優勢[2-3]。不少專家和學者對其進行了深入研究和效率改進，從提高計算速度出發，對分類超平面計算進行效率改進成為該領域一個研究熱點。PSVM[4]、GEPSVM[5]等支持向量機新模型被相繼提出。2007年Jayadeva等人在上述研究成果的基礎上，提出孿生支持向量機(TWSVM)機器學習新方法[6]，其本質上表現為構造兩個不平行的分類超平面，按照離哪類近就歸屬哪類的性質，解決兩個二次規劃問題。由于其計算速度為標準SVM的4倍，TWSVM在圖像檢測、人工識別[7-8]等眾多領域得到了良好應用。并且與一般支持向量分類機、回歸機相比，孿生支持向量機無論在正確率計算、計算速度、優化精度等方面都得到了有效提高[9]。以孿生支持向量分類機為例，其標準數學模型構造為：

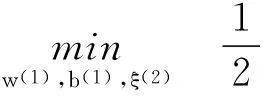
(1)

在線性分類情況下，按照一般支持向量機的求解思路，引入拉格朗日參數，基于KKT條件，對式(1)進行對偶空間內優化求解，計算結果得到形如式(2)所示。其中M=D=[B,e2]T，N =S=[A,e1]T，e1,e2均為值為1的列向量。

(2)

對于拉格朗日參數α和β的尋求，可通過內點法[10]、性能更好的TBSVM[11]等相關算法得到。在非線性分類情況下，依托于SVM中核函數[12]的引入，也可得到相應的數學模型。

式(2)應用了從對偶空間中解決孿生支持向量機的解決問題。但文獻[13-14]通過計算分析表明，TWSVM事實上可直接基于原始數值空間求解優化問題，在原始空間內引入正號函數形成光滑孿生支持向量機模型(STWSVM)，進而通過對正號函數進行逼近，將原模型進行光滑化，從而達到采用梯度算法快速求解目的。Chen等人[15]采用Sigmoid函數作為光滑函數，對孿生支持向量的目標函數作光滑處理，并采用快速算法求解相應的模型。實驗結果都表明了其有效性。文獻[16,17] 基于光滑孿生支持向量機的光滑逼近要求，在總結了大量使用方法的基礎上，提出了使用多項式光滑逼近方式，并且基于一定的標準數據集計算取得了比Sigmoid函數更好的效率優化結果。

光滑函數的選擇是解決這一問題的關鍵所在，本文在總結光滑孿生支持向量機數學形式的基礎上，提出一種基于最佳一致逼近的光滑函數，通過樣本數據的重要度設置樣本數據適應度，最后基于最佳一致光滑逼近函數和適應函數構建新的目標優化函數。相關數據集的實驗驗證，證明了最佳一致孿生支持向量機的可行性。

1 光滑孿生支持向量機

按照所采用光滑方法的不同，其一般運算過程為將式(1)中的松弛變量ξ(1)、ξ(2)由1范式改變為2范式。

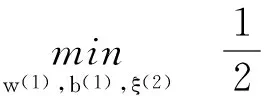
(3)

式(3)中對ξ(1)、ξ(2)具有一定的約束條件，引入正號函數[x]+=max(0,x)，根據KTT條件設置ξ(1)、ξ(2)優化取值，進而引入光滑逼近函數p(x)，其表示了通過一定的函數轉換，把式(3)轉變為兩個無約束優化問題。

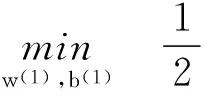
(4)

式(4)變成了可微的目標函數優化問題，可采用具有快速收斂能力的相關算法求解該模型。光滑孿生支持向量機在原始空間更具優勢，理論分析和實驗驗證[15]都表明了其有效性和可行性。

在非線性情況下，基于核函數的孿生支持向量機一對超平面求解目標函數可以表示為：

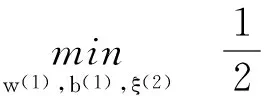
(5)

基于同樣的原理，將式(5)轉換成為無約束目標函數為：

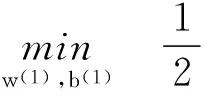
(6)

2 最佳一致逼近光滑函數

光滑函數的選擇是求解式(4)和式(6)數學模型的關鍵，文獻[16,17]指出，基于多項式插值的光滑函數構建是解決約束不可微問題的重要方法。但對于多項表達式的尋求，目前還沒有普遍的方法來構造完成，并且逼近誤差達不到計算需求。最佳一致逼近具有逼近速度快、精度誤差小等特點，為解決上述問題提供了一個良好方法。

(7)

Bn(f)隨著參數n的增大逼近了目標函數f(x)，顯然，正號函數滿足在區間上的連續，基于逼近精度需求，考慮函數在對稱區間[-1,1]逼近，通過變量替代變換到計算區間，可得到與其對應Bernstein多項式為：

(8)

表1表示了Bernstain多項式在區間[-1,1]上對正號函數的逼近多項式。可以看到，隨著逼近的逐次迭代，計算多項式復雜度也得到了較大的提高。

由表1構造的多項式結合文獻[18]對其的精度分析可知，Bernstain多項式對整體的逼近性質要求較好，但收斂速度較慢，提高精度伴隨著多項式次數的提高，這對復雜函數下的多項式逼近工作量較大。但由于正號函數并不復雜，構造表1中Bernstain多項式逼近正號函數不失為一種方法。

表1 Bernstain多項式最佳逼近

與Bernstain多項式逼近相比，Chebyshev逼近是構造最佳逼近多項式的一種較為理想的有效方式。其在構建過程中更強調整體精度性且迭代次數計算并不復雜。其表示對于f(x)∈C[a,b]，要尋求f(x)的n次最佳一致逼近代數多項式pn(x)，問題的關鍵在于確定具有n+2個點的交錯點組{xi}，如果點組存在，則滿足：

(9)

其中η=Δ(f,pn)或者-Δ(f,pn)。由介值定理可知，f(x)-pn(x)在C[a,b]上至少有n+1個零點，pn(x)就是以這n+1個零點為插值點的n次拉格朗日插值多項式。

式(9)是一個關于n+2個變元a0,a1,…,an,η的n+2階線性方程組，存在唯一的解，從而求得最佳逼近多項式pn(x)和最佳逼近|η|。由于尋找交錯點組并不容易，這里應用Remez最佳一致近似算法[14]來求解。其有以下3步構成：

(1) 在區間[a,b]上選擇n+2由小到大的初始點列{x0,x1,…,xn+1}作為交錯點組，設置迭代計算精度ε>0。

(2) 計算式(5)中的方程組，得到{a0,a1,…,an},進而構建pn(x)，計算最佳逼近|η|。

(3) 若Δ(f,pn)=|f(x)-pn(x)|∞-|η|≤ε，則迭代終止，否則利用單一交換、同時交換等方法計算替換新的交錯點組，返回步驟(2)。

依據Remez算法，對光滑孿生支持向量機中的正號函數進行最佳一致Chebyshev多項式逼近。設定初始迭代區間范圍[-1,1]，應用單一交換方法，計算正號函數多項式逼近取值過程，其二次多項式逼近結果如表2所示。

表2 多項式最佳逼近

同理可分別計算得到最佳一致n次Chebyshev多項式，由于Remez算法為逐次逼近近似求解，其并沒有統一的n次多項式表示，表3羅列了n取值不超過5時的Chebyshev多項式及其誤差精度。

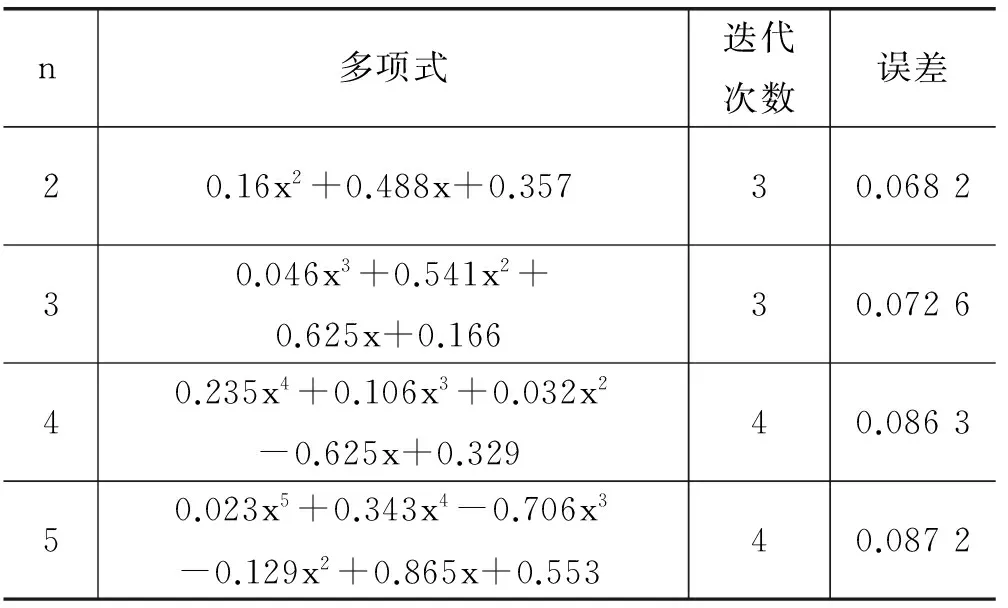
表3 Chebyshev多項式最佳逼近

從表3可以看出，Remez算法的收斂速度相當快，經過3次迭代就可以計算得到結果。圖1表示了樣條插值多項式(黑線)、最佳一致五次Bernstain多項式(細線)、二次Chebyshev多項式(虛線)正號函數逼近效果，從圖形可以知道，最佳一致逼近Chebyshev多項式相比插值多項式、Bernstain多項式取得了良好的逼近效果。

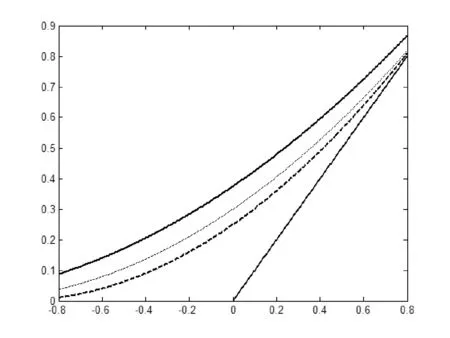
圖1 最佳一致逼近光滑函數

為了綜合考慮樣本離群點對孿生支持向量機的影響，在基于文獻[13]的加權系數設計方式上，這里采用基于距離公式建立各個樣本點的適應度，為了有效表示中心點，離群點及對分類超平面的影響，依據離群點的位置重要度指標形成一個數值向量g1、g2。其值設置為：

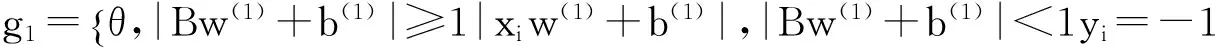
(10)

綜合式(4)，式(10)，在原始空間內對線性孿生支持向量機求值，通過構造最佳一致二次多項式光滑逼近目標函數內的正號函數，得到在區間內的具體優化目標為：

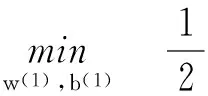
(11)

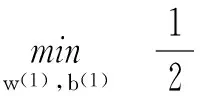
(12)其中R為求得的最佳一致多項式系數。式(11)、式(12)表示了無約束條件下的二次規劃求值，可采用Newton-Armijo算法求解優化模型。其一般計算流程為：

(1) 設定初始點(w(0),γ0)，設置算法精度ε,設置循環計算的初始值k=1。

(2) 計算關于當前迭代點的偏導函數g(k)的值，判斷是否滿足終止條件‖g(k)<ε‖，否則轉(3)。

(3) 求新的迭代點的(w(k),γk)值，根據迭代公式求搜索方向d(k)。

(4) 基于步驟(3)中的尋求目標d(k),依據全局搜索策略步長ak。

(5) 基于上述步驟，迭代公式(w(k+1),γk+1)= (w(k),γk)+d(k)ak，轉(2)。

3 實 驗

為驗證模型有效性，以BUTWSVCM表示最佳一致二次Chebyshev多項式光滑逼近孿生支持向量分類機，以DUTWSVCM表示對偶空間內的孿生支持向量機分類機，BETWSVCM表示Bernstein五次多項式逼近分類機。所有實驗在都在Intel(R)Core(TM)i5-2450MCPU,4GB內存和MATLABr2011b的環境中進行 應用Newton-Armijo算法求解優化模型。設置Remez算法精度ε=1.0E-3，線性算法對數據集的測試結果對比見表4所示。采用一般高斯徑向基函數作為核函數，從UCI數據集中各取100條數據作為測試數據，非線性算法下的訓練和測試結果見表5所示。

表4 線性算法計算結果

表5 非線性算法計算結果 %

從表4、表5中可以看到， BUTWSVM取得了更好的計算速度和精度。采用最佳一致光滑逼近函數求解孿生支持向量機可以得到滿意的結果。

依據表1、表3的多項式表達方式，選取同一UCI數據集，對n(n<6)次最佳一致多項式逼近效果和準確率開展計算分析，計算結果如表6所表示。其表明，相比較于其他同類多項式，Bernstein五次多項式、Chebyshev二次多項式取得了良好效果。也間接驗證了表4、表5的結果最佳性。

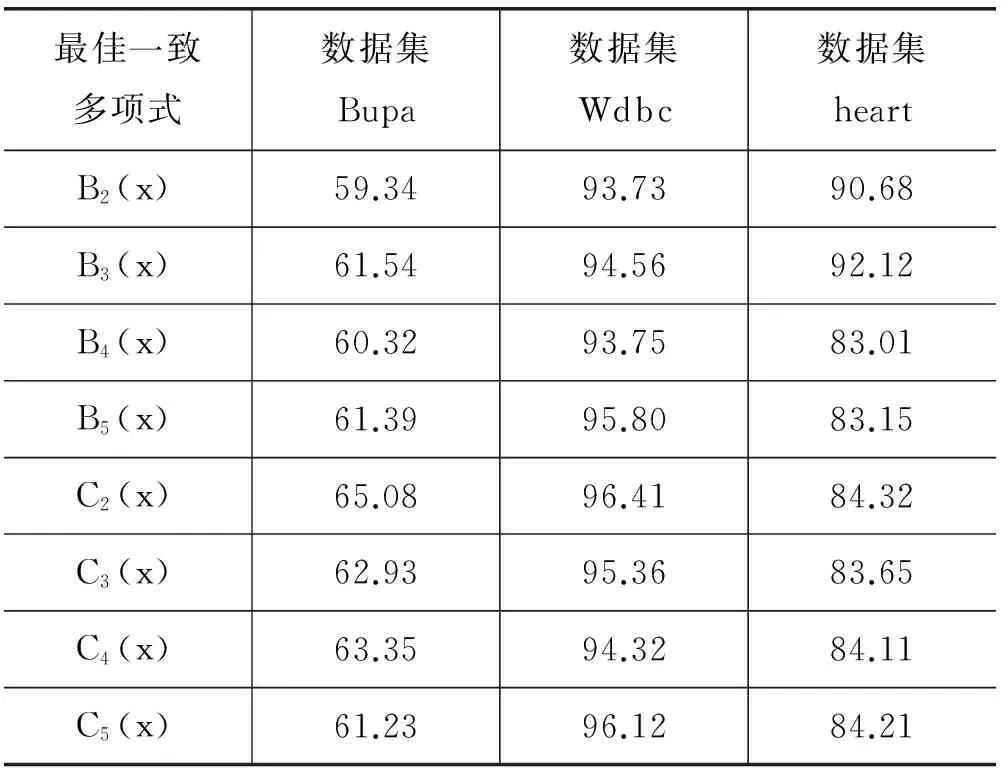
表6 最佳一致多項式分類準確率 %

4 結 語

孿生支持向量機與一般支持向量機相比，在計算效率方面得到了有效提升。本文針對孿生支持向量機原始空間優化求值的需求，構建最佳一致光滑逼近方法孿生支持向量機計算模型。給出了最佳一致二次多項式的推導和計算過程，定義了孿生支持向量機光滑數學模型，基于樣本位置計算了個體適應度。通過實驗仿真可以得到最佳一致光滑多項式能夠有效地逼近原始空間內的正號函數，計算準確率和速度都達到了優化要求。最佳一致光滑逼近函數的建立，對于優化孿生支持向量機計算過程進而達到快速求解目的，提高計算分析準確率具有重要的作用。

[1] Vapnik V N.The Nature of Statistical Learning Theory[M].Springer-Verlag,New York,1995.

[2] Shawe-Taylor J,Sun S.A review of optimization meth- odologies in support vector machines[J].Neurocomputing,2011,74:3609-3618.

[3] Wu J X.Efficient HIK SVM learning for Image Classification[J].IEEE Transactions on Image Processing,2012,21(10):4442-4453.

[4] Fung G,Mangasarian O L.Proximal Support Vector Machine Classifiers[C]//Proc 7thACM SIFKDD Intl Conference on Knowledge Discovery and Data Mining,2001:77-86.

[5] Mangasarian O L,Wild Edward W.Multi-surface proximal support vector machine classification via generalized eigenvalues[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(1):69-74.

[6] Jayadeva K R,Suresh C.Twin support vector machines for pattern classification[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(5):905-910.

[7] Kumar M A,Gopal M.Application of smoothing technique on twin support vector machines[J].Pattern Recognition Letters,2008,29(13):1842-1848.

[8] Khemehandani R,Jadeva S Chajndra.Optimal kernel selection in twin support vector machines[J].Optimization Letter,2009,3:77-88.

[9] Cong H H,Yang C F,Pu X R.Efficient Speaker Recognition based on Multi-class Twin Support Vector Machines and GMMs[C]//2008 IEEE Conference on Robotics,Automation and Mechatronics,2008:348-352.

[10] 袁玉萍,鐘萍,鄒艷華.基于預測-校正原對偶內點法的多分類支持向量機學習算法[J].南京大學學報,2009,45(4):494-498.

[11] Shao Y H,Zhang C H,Wang X B,et al.Improvements on twin support vector machines[J].IEEE Transactions on Neural Networks,2011,22(6):962-968.

[12] Jayadeva R K.Optimal kernel selection in twin support vector machines[J].Optimal Letter,2009,3:77-88.

[13] Wang Z,Shao Y H,Wu T R.A GA-based model selection for smooth twin parametric-margin support vector machine[J].Pattern Recognition,2013,46:2267-2277.

[14] 黃華娟.孿生支持向量機關鍵問題的研究[D].中國礦業大學,2014.

[15] Chen X B,Yang J,Liang J,et al.Smooth twin support vector regression[J].NeuralComputing & Applications,2012,21:505-513.

[16] 熊金志,胡金蓮,袁華強,等.一類光滑支持向量機新函數的研究[J].電子學報,2007(2):8-10.

[17] 陳衛東,范艷峰.基于三次樣條插值的支持向量機研究[J].計算機工程與設計,2009,30(7):1722-1725.

[18] 蔣爾雄.數值逼近[M].上海:復旦大學出版社,2007.

RESEARCH ON TWIN SUPPORT VECTOR MACHINES BASED ON BEST UNIFORM SMOOTHING APPROXIMATION

Tang Huijun1Bai Ling1Yang Zhimin2

1(CollegeofInformationEngineering,NingboDahongyingUniversity,Ningbo315175,Zhejiang,China)2(CollegeofZhijiang,ZhejiangUniversityofTechnology,Hangzhou310023,Zhejiang,China)

The essence of twin support vector machines(TWSVM) is to optimise two quadratic programming problems. As the positive constrained variable of objective function was not differentiable, this paper presented a constructing method of polynomial smoothing function based on best uniform approximation. Bernstein and Chebyshev polynomial were established to effectively achieve the best uniform smoothing approximation of the positive function. The best uniform approximation of Chebyshev polynomial is emphasized. The best uniform Chebyshev polynomial was established by applying the Remez algorithm, and each order of the Chebyshev polynomial approximation was discussed. Finally, the objective optimal function based on best uniform approximation polynomial and the degree of sample adaption could be got, and the fast Newton-Armijo algorithm was used for solving the objective optimal function. On the basis of UCI data, we validated the advantages of the method.

Twin support vector machines Best uniform approximation Degree of adaption

2015-12-07。國家自然科學基金項目(10926198)；浙江省公益技術應用研究計劃項目(2016C33G2620016)；寧波市自然科學基金項目(2015A610135)。唐輝軍，講師，主研領域：數據挖掘，計算機仿真。白玲，碩士生。楊志民，教授。

TP18

A

10.3969/j.issn.1000-386x.2017.04.030