基于Kent混沌測量矩陣的壓縮感知圖像重構算法

孫憲坤 陳 濤 韓 華 王裕明

(上海工程技術大學電子電氣工程學院 上海 201620)

基于Kent混沌測量矩陣的壓縮感知圖像重構算法

孫憲坤 陳 濤 韓 華 王裕明

(上海工程技術大學電子電氣工程學院 上海 201620)

圖像重構是圖像數字化和恢復高質量圖像信號的關鍵技術，使用壓縮感知理論進行圖像重構的意義在于顯著減少采樣次數，降低系統資源的消耗。測量矩陣的構造是壓縮感知的重要研究內容之一。提出一種基于Kent混沌測量矩陣的壓縮感知圖像重構算法，將Kent混沌序列作為測量矩陣，采用離散小波變換的稀疏化方法，在小波域對原始圖像信號進行測量。最后采用正交匹配追蹤方法恢復原始圖像。仿真實驗中，對比高斯隨機測量矩陣和Logistic混沌測量矩陣，對不同的圖像進行重構。實驗結果證明，基于Kent混沌測量矩陣的重構算法能夠恢復原始圖像，重構性能優于高斯隨機觀測矩陣和Logistic混沌測量矩陣，同時克服了隨機測量矩陣硬件難以實現的缺陷。

混沌矩陣 壓縮感知 圖像重構 Kent矩陣

0 引 言

客觀世界的圖像轉換成計算機可以處理的圖像，即圖像的數字化過程，對圖像的采集和存儲等硬件設備要求極高。圖像重構技術的意義在于提高圖像數字化過程中圖像的采集和存儲效率，避免圖像質量退化，盡可能恢復接近實際的圖像。近年來壓縮感知[1-3]CS(Compressive Sensing)作為一種新的采樣理論被廣泛應用于信號處理鄰域。壓縮感知理論使得信號的采樣速率在遠低于信號最高頻率的2倍時，即在不滿足奈奎斯特-香農(Nyquist-Shannon)采樣定理的條件下，也能夠精確重構原始信號。壓縮感知在采樣的同時對信號進行了壓縮，使得圖像重構過程中消耗的系統資源大大減少，降低了成像系統的硬件負擔。壓縮感知理論要求測量矩陣應該滿足約束等距性條件RIP(Restricted Isometry Property)[4]，即測量矩陣和稀疏表達矩陣成不相關關系。測量矩陣的研究是壓縮感知理論的一個重要方面。尋找合適的滿足RIP條件的測量矩陣可以極大地提高信號重構的準確程度并減少硬件設計上的復雜程度。測量矩陣包含隨機測量矩陣和確定性測量矩陣[5]。其中，隨機高斯矩陣[6]和隨機伯努利矩陣[7]，與大多數固定正交基構成的矩陣不相關，但這類隨機矩陣的計算復雜度高，所需存儲空間大。

確定性測量矩陣，如Toeplitz測量矩陣、循環測量矩陣、多項式測量矩陣等[8]，計算復雜度低，克服了隨機測量矩陣的不足。混沌矩陣作為一種確定性測量矩陣，具備偽隨機性，計算過程簡單，硬件上容易實現，在某些要求安全性和保密性的應用上具有優勢。文獻[9]的作者通過Logistic混沌序列構造測量矩陣，證明了托普利茲結構的混沌矩陣在很大程度上滿足RIP準則，并且與高斯隨機矩陣和稀疏隨機矩陣具有相似的重構效果。Kafedziski利用Chua和Lorenz混沌信號構造測量矩陣[10]，證明了測量序列的相關關系不影響重構的準確率。Frunzete和Liu通過帳篷(Tent)混沌序列構造測量矩陣[11-12]，提出了一種新的測量矩陣構造方法。文獻[13]通過Chebyshev映射構造測量矩陣，證明了Chebyshev混沌序列以極大概率滿足RIP準則。文獻[14]對多種混沌映射用作測量矩陣的性能進行了研究，大部分混沌測量矩陣的性能優于隨機高斯矩陣。這些算法與隨機高斯矩陣的重構效果相似。

Kent序列是混沌序列的一種。Kent序列對初始條件的敏感性，比Logistic等混沌序列較好的均勻分布特性，以及良好的類隨機性和遍歷性，使得Kent序列在全局優化[15-16]和圖像加密[17-18]等方面取得了很好的應用效果。目前為止的所有文獻中，還沒有人將Kent序列用于壓縮感知。Kent混沌測量矩陣的類隨機性、遍歷性、均勻分布特性，可以保證在觀測信號時，保留各個頻率分段的豐富信息，在低采樣率條件下，仍能為重構圖像提供有用的觀測信號。因此，本文將Kent序列用于構造壓縮感知的測量矩陣，采用離散小波變換DWT(Discrete Wavelet Transform)[19]方法稀疏表示信號，重構方法為正交匹配追蹤算法OMP(Orthogonal Matching Pursuit)[20]，重構二維的圖像信號。本文的主要貢獻在于提出一種新的混沌序列Kent用于構造壓縮感知的測量矩陣。

1 壓縮感知理論

設X為長度N的一維信號，稀疏度為k(即含有k個非零值)。X在一個N×N維正交變換矩陣Ψ∈RN×N下能表示為：

X=ΨΘ

(1)

其中，Θ=[θ1,θ2,…,θN]T稱為信號X在基矩陣Ψ下的投影系數向量。當信號X在某個正交基Ψ上僅有K?N個非零系數θk時，稱Ψ為信號X的稀疏基，θ是K稀疏的。式(1)將現實中非稀疏的信號進行轉換，稱為信號的稀疏化。常用的稀疏變換有：傅里葉變換、離散余弦變換DCT[21]和離散小波變換(DWT)[19]。而DWT能克服DCT的不足，如方塊效應等，獲得更好的圖像恢復效果。

利用觀測矩陣Φ∈RM×N對信號進行觀測，即可獲得觀測值Y：

Y=ΦΘ=ΦΨ-1X

(2)

在已知Y、Φ和Ψ，并且Φ滿足RIP準則(式(3))的條件下，用l1范數逼近l0范數，通過求解非線性優化問題，即可從Y中恢復原始信號X。

(3)

目前壓縮感知的重構算法包括：匹配追蹤MP(MatchingPursuit)算法(OMP[20]、CoSaMP算法[22])，重構速度快，但重構精度不高；子空間追蹤SP(SubspacePursuit)[23]，方向追蹤GP(GradientPursuit)算法[24](GP、CGP、ACGP)；凸優化算法(如BasisPursuit(BP)[25]、LeastAngleRegression(LARS)[26]、GradientProjectionforSparseReconstruction(GPSR)[27])，它們的計算量較大；以及基于貝葉斯的算法[28-30]，其重構性能介于匹配追蹤算法和凸優化算法之間。

2 Kent混沌測量矩陣

Kent映射是一種具有代表性的離散混沌系統，其系統方程可以表示為：

(4)

其中，控制參數a∈(0,1)。圖1-圖3顯示了Kent映射具備的特性。

如圖1為Kent映射的分岔圖。由于計算機字節長度和精度的限制，在a=0.5時Kent映射容易周期化或者收斂于固定值。為了生成可靠的Kent混沌序列，本文取a=0.4。從圖1可以看出，當a∈(0,1)，x∈(0,1)時，Kent映射處于混沌狀態，體現了Kent映射的類隨機性。

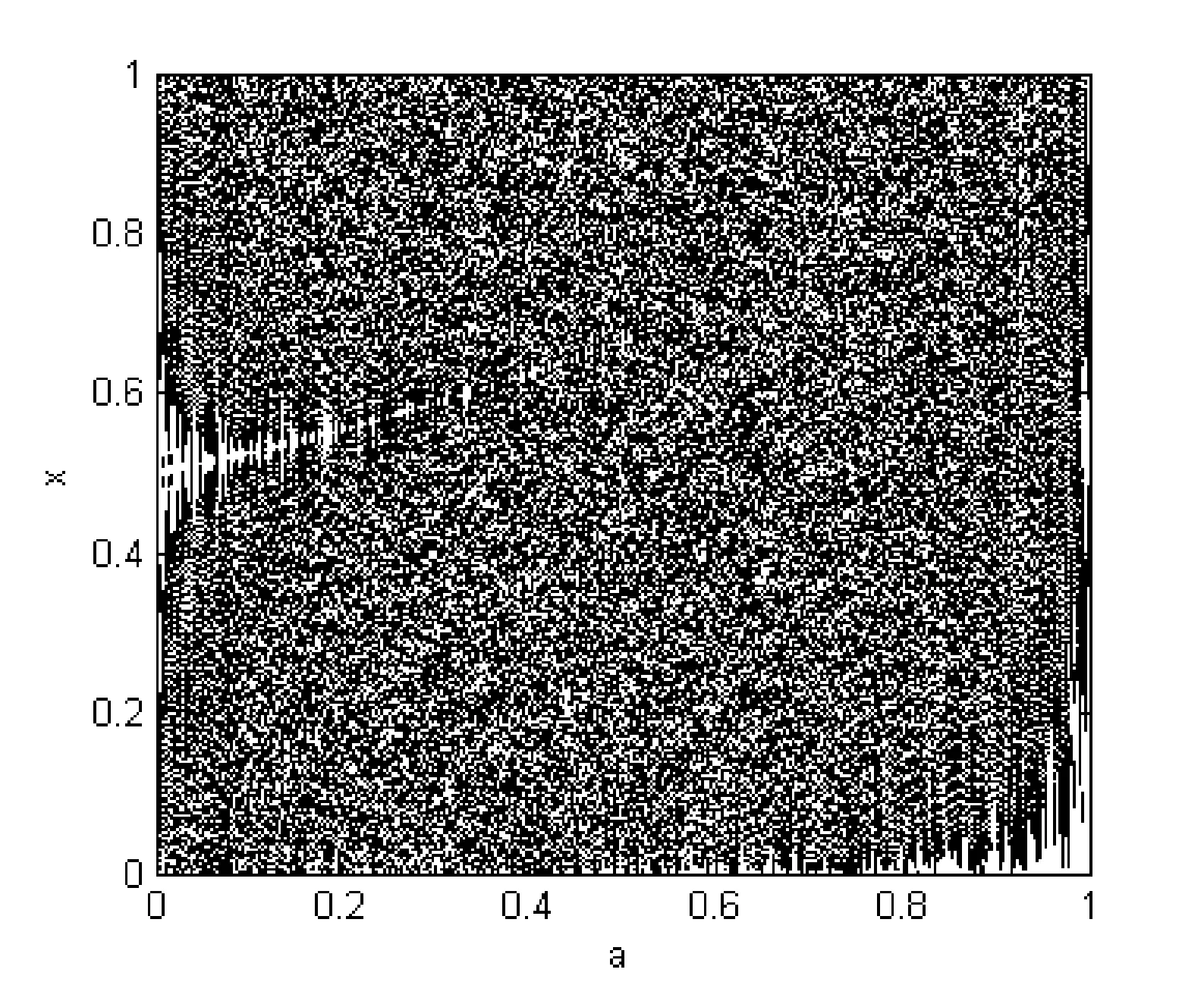
圖1 Kent映射分岔圖

圖2所示為Kent映射的Lyapunov指數圖。Lyapunov指數用來刻畫混沌系統初始狀態微小不確定性的發散比率和混沌水平，一維混沌系統xn+1=f(xn)的Lyapunov指數[16,31]可以表示為：

(5)

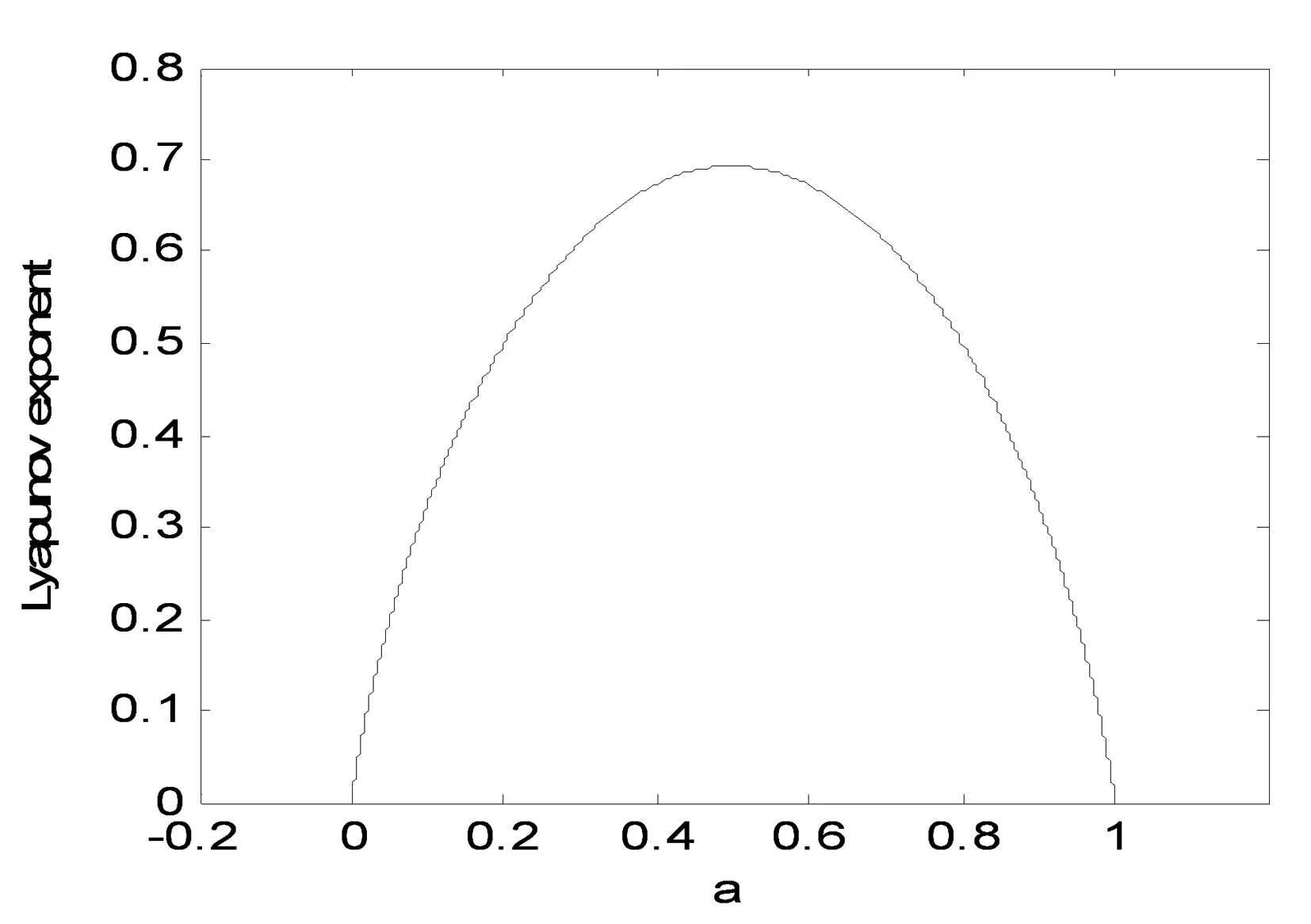
圖2 Kent映射的Lyapunov指數圖

圖2中Kent映射的Lyapunov指數曲線均在x軸上方，因此Kent映射在a∈(0,1)內是混沌的，具備良好的遍歷性。

Kent映射的概率密度d(x)服從均勻分布，由式(6)Frobenious-Perron方程[32]計算得到，即：

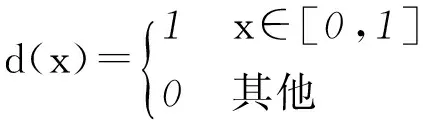
(6)

(7)

圖3為四種測量矩陣或映射的概率分布直方圖。圖3(a)-(d)分別為Kent、Gaussian、Bernoulli、Logistic矩陣的隨機分布特性，它們的矩陣元素數量都為10 000個。可以看出，Gaussian矩陣呈鐘型分布，在圖像重構時重點觀測了主要信號，Bernoulli矩陣的分布中，只有元素0和1，它們等概率的出現。Logistic映射的概率分布中部均勻，兩端偏高。圖3(a)為Kent映射在[0,1]上的概率分布直方圖，圖中顯示Kent映射在各區間呈均勻分布，有利于提取圖像重構信號。

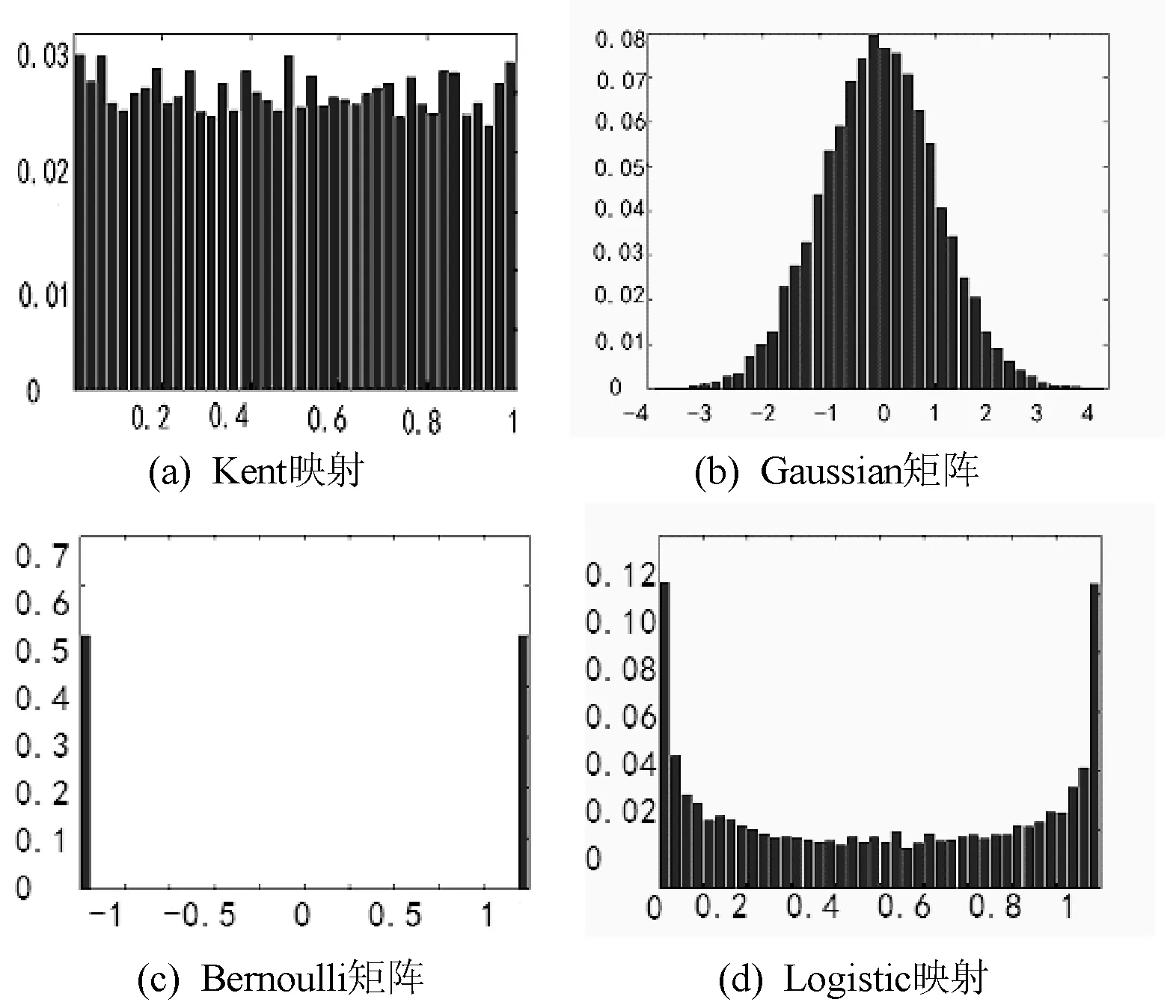
圖3 四種概率分布直方圖

Kent混沌映射的初始值一旦確定，系統的每一項都可以完全重現，大大減少所需的存儲空間，且硬件實現簡單。Kent映射良好的類隨機性、遍歷性以及均勻分布的這些特性，適用于壓縮感知測量矩陣的生成，易于產生和重現。Kent序列的平均性及穩定性也有利于信號的重構。

利用迭代產生的序列{x0,x1,…,xn}構建M×N的測量矩陣，Kent混沌測量矩陣的構造如下：

(8)

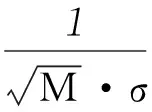
圖4 Kent混沌測量矩陣Φ(Size:128×256,M=128;此時σ=0.0834)

3 基于Kent測量矩陣的壓縮感知

壓縮感知是利用信號的稀疏特性重構原始信號的方法。在壓縮感知理論中，Kent等測量矩陣用于對稀疏變換進行觀測測量，得到待重建的觀測信號。稀疏表示完成對原始信號的轉化，變換成稀疏信號。重構算法實現觀測信號的恢復重建。本文壓縮感知重構算法流程見圖5所示。

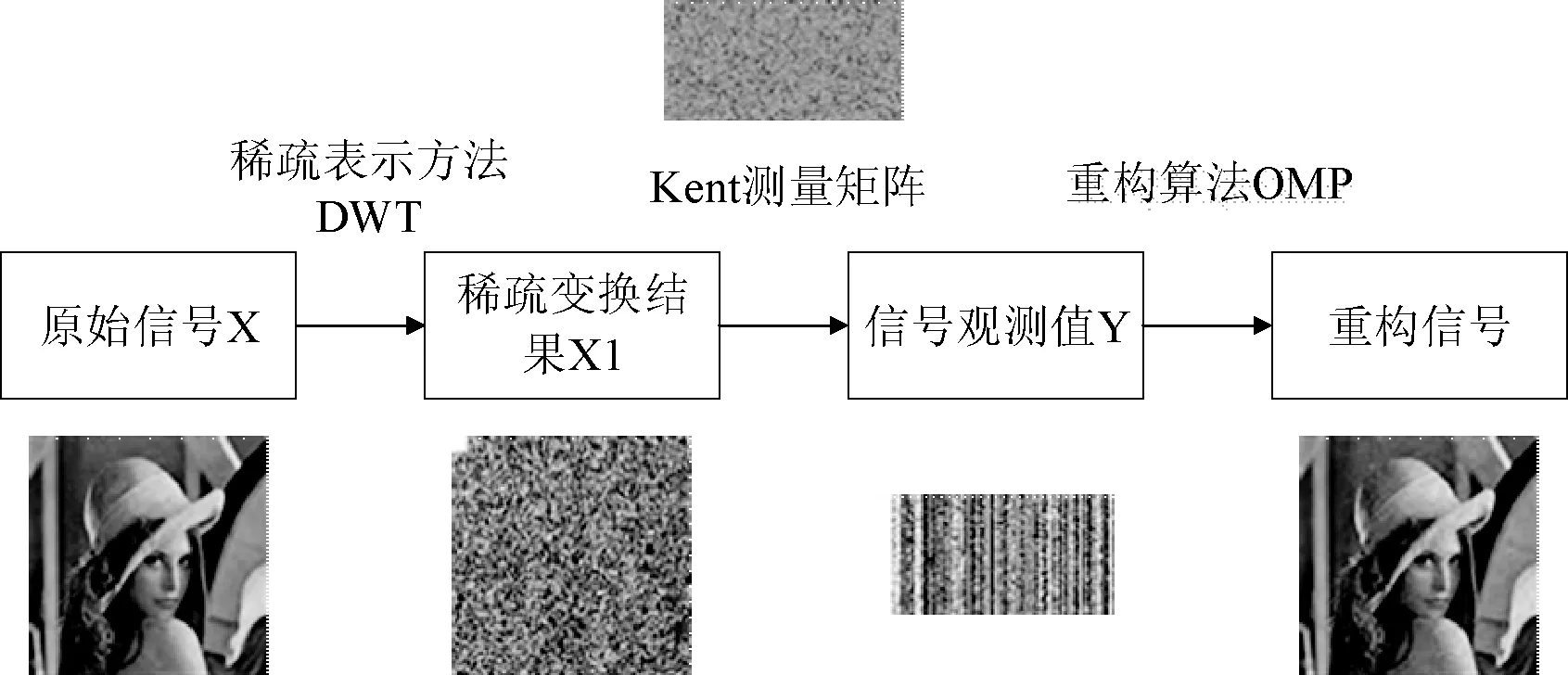
圖5 Kent測量矩陣壓縮感知圖像重構流程

如圖5所示，本文首先采用離散小波變換(DWT)作為稀疏基Ψ對圖像進行稀疏表示，再利用Kent測量矩陣完成信號的觀測，最后采用正交匹配追蹤(OMP)算法對圖像進行恢復重建。

3.1 離散小波變換

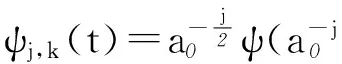
Wf(j,k)=[f(t),ψj,k(t)]=∫Rf(t)ψj,k(t)dt

(9)

圖像可以用二維矩陣X表示，ωω表示經過一維離散小波變換的正交規范化變換矩陣。則圖像X的離散小波變換為：

X1=ωω×X×ωω′

(10)

如圖6所示為經過上述離散小波變換的正交規范化矩陣，其中，空白區域為零元素，藍色部分為非零元素的分布，可以看出矩陣是稀疏的。我們將其用于圖像的稀疏變換，圖像經過離散小波變換之后的結果如圖5中的X1所示，X1即為稀疏變換之后的圖像信號。

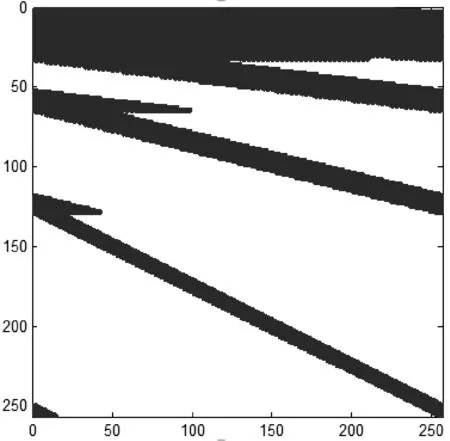
圖6 離散小波變換得到的稀疏矩陣ωω的結構圖(藍色為非零元素的分布)

測量矩陣Φ再對圖像信號進行測量，測量值用Y表示：

Y=Φ×X1

(11)

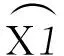
3.2 正交匹配追蹤算法

正交匹配追蹤(OMP)算法以貪婪迭代的方式，使得測量矩陣的每一列與當前的殘差向量最大程度的相關，再從矩陣中減去相關部分，反復迭代直到滿足稀疏條件[20]。

輸入：測量向量y，測量矩陣Φ，稀疏度K。

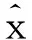
初始化：殘差r0=y，索引集Λ0=?，迭代次數t=1。

OMP算法核心步驟如下：

步驟2 更新索引集Λt=Λt-1∪{λt}，記錄找到的測量矩陣中的重構原子集合Φt=[Φt-1,φλt]；

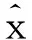
在圖像信號重建過程中，OMP算法對圖像的每一列數據分別進行恢復，如圖7所示，為OMP算法對圖像信號的一列數據進行的恢復結果。兩張圖像的曲線及其相似，信號完整，說明OMP算法對圖像信號進行了有效的恢復。

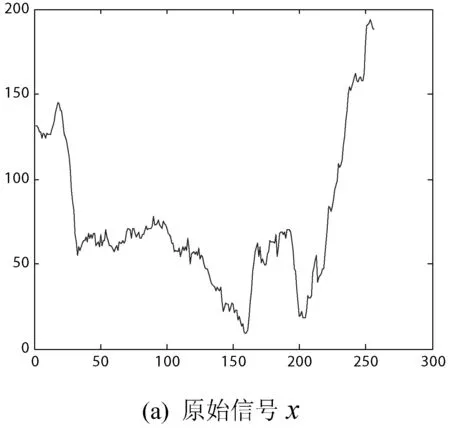
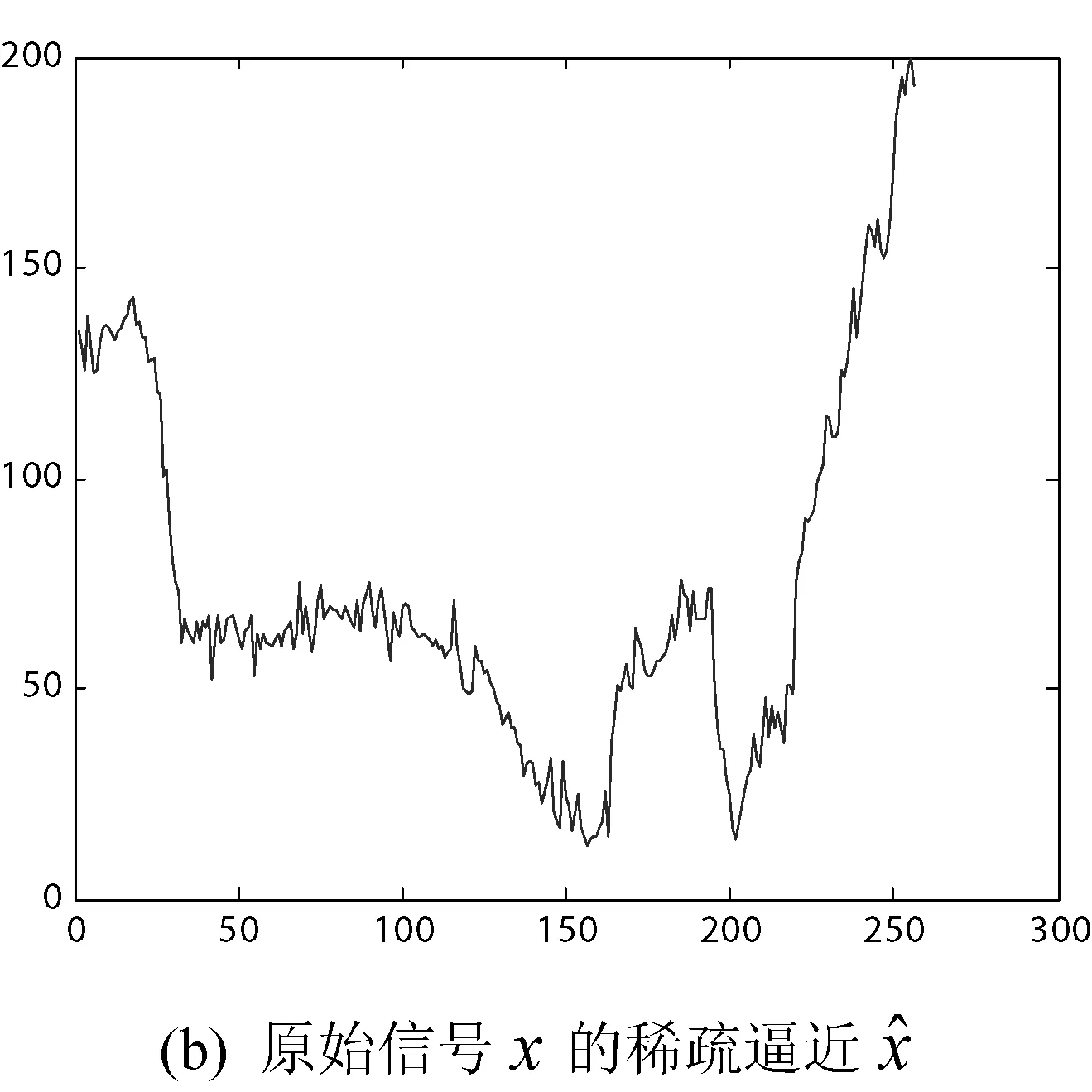
圖7 正交匹配追蹤(OMP)算法恢復圖像信號

4 仿真實驗

本文將比較隨機高斯矩陣、隨機伯努利矩陣、Logistic混沌矩陣和Kent混沌矩陣作為測量矩陣時的性能。對于M×N的測量矩陣，取采樣率R=M/N=0.5。為了生成更好的混沌測量矩陣，以獲得更加準確的檢測效果，Logistic和Kent混沌序列的前面一小段被截去。Kent混沌測量矩陣的控制參數a=0.4。本文采用大小為256×256的灰度圖像作為測試目標，圖像重構效果見圖8所示。實驗環境為MATLAB2013a，計算機CPU性能參數為i5-2410M2.3GHz，內存大小為4.00GB。本文采用了兩種不同的圖像質量評價指標，峰值信噪比PSNR和結構相似性指標SSIM，來評價重構圖像的質量。

圖8 不同測量矩陣圖像重構效果對比

4.1 峰值信噪比PSNR

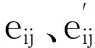
PSNR=10log10(2552/MSE)

(12)

(13)

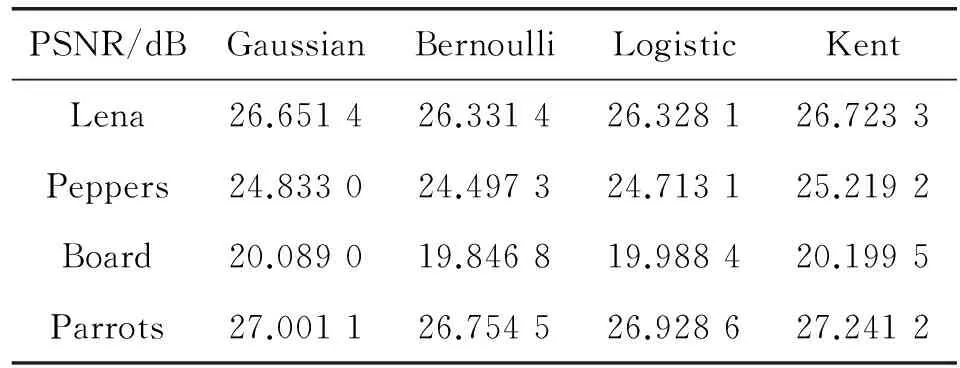
表1 采樣率為0.5時，各測量矩陣重構圖像的PSNR值

如表1的數據顯示，在相同的采樣率條件下，Kent測量矩陣重構的圖像質量與使用隨機高斯矩陣的重構結果相近，并且是四種測量矩陣中重構效果最好的。其中，對于隨機伯努利矩陣，除了Lena圖的PSNR值比Logistic混沌測量矩陣的稍大一些，其他圖像的PSNR值均最小，說明其重構準確度最差。同理，Logistic混沌測量矩陣的圖像重構效果稍差，而隨機高斯矩陣的圖像重構效果較前兩者要好。Kent混沌測量矩陣的四幅圖像的PSNR值都是最大，說明其圖像恢復的準確程度最高，圖像重構效果最好。

為了進一步驗證本文提出的Kent混沌測量矩陣在重構精度上的優勢，本文在不同的采樣率下，用上述測量矩陣對圖像進行重構。采樣率在0.2～0.6時，各測量矩陣重構結果的PSNR變化如圖9所示。

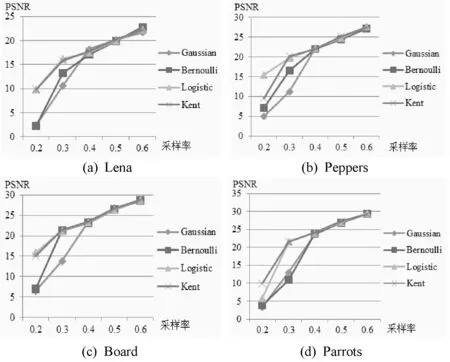
圖9 各測量矩陣在不同采樣率下的PSNR(dB)變化圖

從圖9可以看出，隨著采樣率的提高，圖像的重構精度也在提高。說明測量矩陣測量的圖像數據越多，恢復的圖像信息也越準確。圖9中，在采樣率為0.2～0.3時，Logistic和Kent混沌測量矩陣的重構精度比Gaussian和Bernoulli隨機測量矩陣要高。在采樣率為0.4～0.6時，四種測量矩陣的重構精度差別不大。

4.2 結構相似性指標SSIM

鑒于圖像結構表達信息的重要性，我們采用符合人眼主觀感知的結構相似性SSIM指標[34]：

(14)

其中：μ為圖像均值，σ為圖像方差或協方差，c1和c2為避免分母為零的小常數。SSIM值越大(最大為1)，則重構圖像與原圖像越逼近，從而算法效果越好。表2給出了采樣率為0.5時，各測量矩陣的SSIM值。

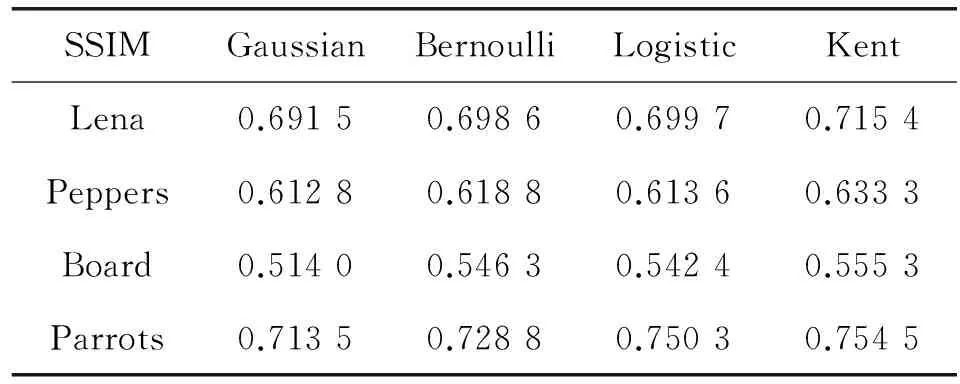
表2 采樣率為0.5時，各測量矩陣重構圖像的SSIM值

從表2中不同測量矩陣重構圖像的SSIM值可以看出，對于四種不同的圖像，Kent測量矩陣重構圖像的SSIM值始終最大，說明采用Kent測量矩陣重構的圖像與原圖像最逼近，重構效果最好。其中，Gaussian測量矩陣重構圖像的SSIM值始終最小，重構效果最差。而Bernoulli測量矩陣和Logistic測量矩陣圖像重構的SSIM值介于前兩者之間，說明它們的重構效果比Gaussian矩陣好，但比Kent矩陣差。

圖10為各測量矩陣在不同采樣率下的SSIM變化圖。從圖10可以看出，隨著采樣率的提高，圖像的SSIM值也越高，說明重構的圖像越來越逼近原圖。圖10中，在采樣率為0.2～0.3時，Logistic和Kent混沌測量矩陣的SSIM值比Gaussian和Bernoulli隨機測量矩陣要高，說明前采用兩種測量矩陣重構的圖像更逼近原圖。圖9、圖10中(b)可以看出，對于Pepper圖像在低采樣率的情況下Kent混沌序列作為測量矩陣，其重構效果不如Logistic矩陣，說明在個別圖像中Kent矩陣的重構效果較差，但相比隨機測量具有明顯的重構效果。在采樣率為0.4～0.6時，四種測量矩陣的SSIM值差別不大，說明四種測量矩陣的重構效果基本一致。以上SSIM評價指標的結論與PSNR評價指標得到的結論相同，再次驗證了采用Kent矩陣作為壓縮感知測量矩陣的有效性。

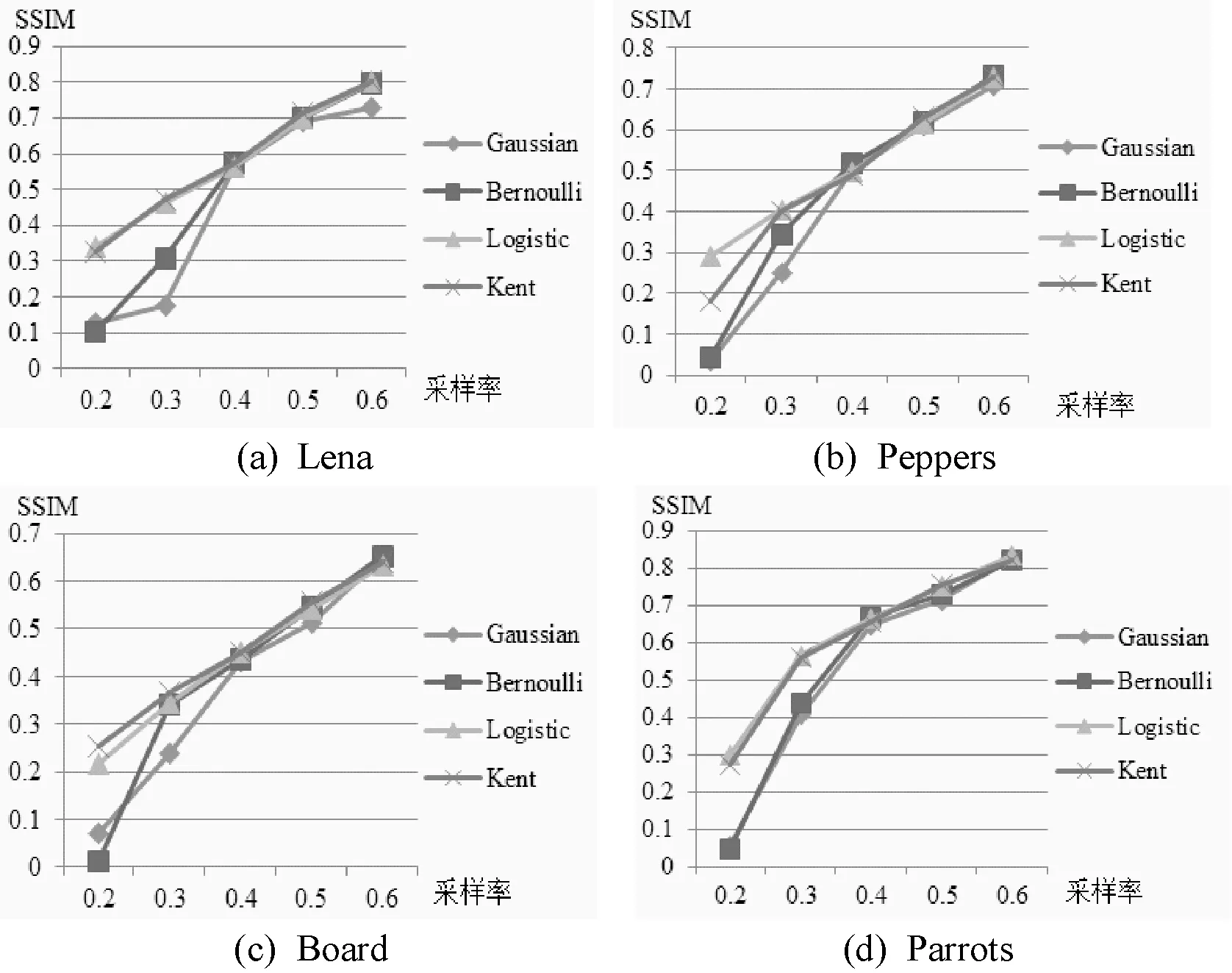
圖10 各測量矩陣在不同采樣率下的SSIM變化圖

為了從視覺上直觀地觀察這一現象，本文在圖11-圖14中給出了四種圖像的重構結果。

圖11 不同采樣率R條件下的Lena圖像重構結果

圖12 不同采樣率R條件下的Peppers圖像重構結果

圖13 不同采樣率R條件下的Board圖像重構結果

圖14 不同采樣率R條件下的Parrots圖像重構結果

如圖11-圖14所示，隨著采樣率的降低，各測量矩陣重構的圖像越來越模糊，即重構精度逐漸降低。從圖中可以看出，在低采樣率下，圖像會出現塊狀效應，導致重構精度嚴重降低。塊狀效應在隨機測量矩陣(Gaussian、Bernoulli)的重構圖像中更加嚴重，而混沌測量矩陣(Logistic、Kent)在低采樣率下，仍可重構出圖像的大致輪廓。結合圖3，根據測量矩陣的隨機分布特性分析上述重構效果的差異。對于Gaussian和Bernoulli矩陣，當采樣率降低時，如圖11-圖14(d)、(e)，測量矩陣的元素減少，由于矩陣元素是隨機產生的，這時不能滿足上述隨機分布特性，造成對個別頻段信息的提取不足，重構效果變差。圖3(d)中Logistic矩陣呈兩頭偏高的均勻分布，圖3(a)中Kent矩陣的分布特性較其他矩陣都均勻，由于是確定性矩陣，在矩陣元素量減少時，它們的分布特性保持不變，對各頻段信息的提取能夠得到保證，因此重構效果較隨機矩陣優。

結合圖11-圖14的重構效果，當采樣頻率越低時，獲取圖像信號的信息量越少。在采樣率較低時，Gaussian和Bernoulli隨機測量矩陣的隨機分布特性較差，所觀測的信號丟失了有用信息，不足以恢復原始信號。而Kent混沌測量矩陣分布更加均勻，比Logistic矩陣的隨機分布性能更好，能夠有效觀測到各頻率分段的信號，因此，Kent矩陣在重構圖像時質量更好。提高采樣率可以獲取更精確的圖像，但采樣率的提高，增加了要處理的數據量，因此實際應用中需要根據具體條件在處理速度和圖像精度上合理取舍。

5 結 語

本文針對壓縮感知中的測量矩陣構造問題，提出了基于Kent混沌測量矩陣的壓縮感知圖像重構算法。混沌矩陣具備構造簡單，占用存儲空間少等優勢，相比高斯、伯努利等隨機矩陣，在消耗較低硬件代價的同時，仍可以觀測到各頻段的有用信號，獲得不遜于隨機矩陣的重構精度。在不同采樣率下進行的圖像重構實驗表明，Kent混沌測量矩陣在低采樣率下的圖像重構效果更好，比隨機測量矩陣提高至少4～5 dB，具有一定應用價值。今后將在降低塊狀效應，提高重構精度方面作進一步的研究。

[1] Donoho D L.Compressed sensing[J].Information Theory,IEEE Transactions on,2006,52(4):1289-1306.

[2] Baraniuk R G.Compressive sensing[J].IEEE signal processing magazine,2007,24(4).

[3] 李然,干宗良,朱秀昌.基于最佳線性估計的快速壓縮感知圖像重建算法[J].電子與信息學報,2012,34(12):3006-3012.

[4] Candès E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique,2008,346(9):589-592.

[5] 豐祥,萬旺根.運用壓縮感知理論的圖像稀疏表示與重建[J].應用科學學報,2014,32(5):447-452.

[6] Monajemi H,Jafarpour S,Gavish M,et al.Deterministic matrices matching the compressed sensing phase transitions of Gaussian random matrices[J].Proceedings of the National Academy of Sciences,2013,110(4):1181-1186.

[7] Mendelson S,Pajor A,Tomczak-Jaegermann N.Uniform uncertainty principle for Bernoulli and subgaussian ensembles[J].Constructive Approximation,2008,28(3):277-289.

[8] 王俠,王開,王青云,等.壓縮感知中的確定性隨機觀測矩陣構造[J].信號處理,2014,30(4):436-442.

[9] Yu L,Barbot J P,Zheng G,et al.Toeplitz-structured chaotic sensing matrix for compressive sensing[C]//Communication Systems Networks and Digital Signal Processing (CSNDSP),2010 7th International Symposium on.IEEE,2010:229-233.

[10] Kafedziski V,Stojanovski T.Compressive sampling with chaotic dynamical systems[C]//Telecommunications Forum (TELFOR),2011 19th.IEEE,2011:695-698.

[11] Frunzete M,Yu L,Barbot J P,et al.Compressive sensing matrix designed by tent map,for secure data transmission[C]//Signal Processing Algorithms,Architectures,Arrangements,and Applications Conference Proceedings (SPA),2011.IEEE,2011:1-6.

[12] 劉敘含,申曉紅,姚海洋,等.基于帳篷混沌觀測矩陣的圖像壓縮感知[J].傳感器與微系統,2014,33(9):26-28.

[13] Gan H,Li Z,Li J,et al.Compressive sensing using chaotic sequence based on Chebyshev map[J].Nonlinear Dynamics,2014,78(4):2429-2438.

[14] Chen G,Zhang D,Chen Q,et al.The characteristic of different chaotic sequences for Compressive Sensing[C]//Image and Signal Processing (CISP),2012 5th International Congress on.IEEE,2012:1475-1479.

[15] Yang D,Li G,Cheng G.On the efficiency of chaos optimization algorithms for global optimization[J].Chaos,Solitons & Fractals,2007,34(4):1366-1375.

[16] Yang D,Liu Z,Zhou J.Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(4):1229-1246.

[17] Wang X,Wang Q.A novel image encryption algorithm based on dynamic S-boxes constructed by chaos[J].Nonlinear Dynamics,2014,75(3):567-576.

[18] Wang S,Sun W,Guo Y,et al.Design and Analysis of Fast Image Encryption Algorithm based on Multiple Chaotic Systems in Real-time Security Car[J].International Journal of Security & Its Applications,2013,7(6).

[19] 解成俊,張鐵山.基于壓縮感知理論的圖像重構算法研究[J].計算機應用與軟件,2012,28(4):49-53.

[20] 林斌,彭玉樓.基于混沌序列的壓縮感知測量矩陣構造算法[J].計算機工程與應用,2013,49(23):199-202.

[21] Zhang Z,Jung T P,Makeig S,et al.Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware[J].Biomedical Engineering,IEEE Transactions on,2013,60(1):221-224.

[22] Needell D,Tropp J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321.

[23] 吳延海,閆迪.基于改進SP算法的壓縮感知圖像重構[J].計算機應用與軟件,2013,30(7):200-203.

[24] Blumensath T,Davies M E.Gradient pursuits[J].Signal Processing,IEEE Transactions on,2008,56(6):2370-2382.

[25] Lu W,Vaswani N.Modified basis pursuit denoising (modified-bpdn) for noisy compressive sensing with partially known support[C]//Acoustics Speech and Signal Processing (ICASSP),2010 IEEE International Conference on.IEEE,2010:3926-3929.

[26] Efron B,Hastie T,Johnstone I,et al.Least angle regression[J].The Annals of statistics,2004,32(2):407-499.

[27] Figueiredo M A T,Nowak R D,Wright S J.Gradient projection for sparse reconstruction:Application to compressed sensing and other inverse problems[J].Selected Topics in Signal Processing,IEEE Journal of,2007,1(4):586-597.

[28] Poli L,Oliveri G,Rocca P,et al.Bayesian compressive sensing approaches for the reconstruction of two-dimensional sparse scatterers under TE illuminations[J].Geoscience and Remote Sensing,IEEE Transactions on,2013,51(5):2920-2936.

[29] Oliveri G,Rocca P,Massa A.Reliable diagnosis of large linear arrays—a Bayesian compressive sensing approach[J].Antennas and Propagation,IEEE Transactions on,2012,60(10):4627-4636.

[30] Carlin M,Rocca P,Oliveri G,et al.Directions-of-arrival estimation through Bayesian compressive sensing strategies[J].Antennas and Propagation,IEEE Transactions on,2013,61(7):3828-3838.

[31] Yang D,Li G,Cheng G.Convergence analysis of first order reliability method using chaos theory[J].Computers & structures,2006,84(8):563-571.

[32] Nie X,Coca D.Reconstruction of one-dimensional chaotic maps from sequences of probability density functions[J].Nonlinear Dynamics,2015,80(3):1373-1390.

[33] HuynhThu Q,Ghanbari M.Scope of validity of PSNR in image/video quality assessment[J].Electronics Letters,2008,44(13):800-801.

[34] Wang Z,Bovik A C,Sheikh H R,et al.Image quality assessment: from error visibility to structural similarity[J].Image Processing,IEEE Transactions on,2004,13(4):600-612.

COMPRESSED SENSING IMAGE RECONSTRUCTION ALGORITHM BASED ON KENT CHAOTIC MEASUREMENT MATRIX

Sun Xiankun Chen Tao Han Hua Wang Yuming

(SchoolofElectronicandElectricalEngineering,ShanghaiUniversityofEngineeringScience,Shanghai201620,China)

Image reconstruction is the key technique of image digitisation and restoration of high-quality image signal. The significance of using compressed sensing theory to reconstruct the image is to reduce the sampling times and decrease the consumption of system resources. The structure of measurement matrix is one of the important research contents of compressed sensing. This paper presents a compressed sensing image reconstruction algorithm based on Kent chaotic measurement matrix. We use Kent chaotic sequence as the measurement matrix and adopt sparse method for discrete wavelet transform to measure the original image signal in wavelet domain. Finally, we use the orthogonal matching pursuit method to recover the original image. In simulation experiments, Gaussian random measurement matrix and Logistic chaotic measurement matrix are compared in the reconstruction of different images. Experimental results show that the reconstruction algorithm based on Kent chaotic measurement matrix can reconstruct the original image, its reconstruction performance is superior to Gaussian random measurement matrix and Logistic chaotic measurement matrix, and the defects which random measurement matrix hardware cannot realize are overcome.

Chaotic matrix Compressed sensing Image reconstruction Kent matrix

2015-11-16。國家自然科學基金項目(61305014)；上海市教育委員會重點創新項目(14ZZ156)。孫憲坤，副教授，主研領域：圖像處理，計算機應用。陳濤，碩士生。韓華，博士。王裕明，教授。

TP391

A

10.3969/j.issn.1000-386x.2017.04.036