模糊加權多視角可能性聚類算法

王振輝 夏鴻斌

(江南大學數字媒體學院 江蘇 無錫 214122)

模糊加權多視角可能性聚類算法

王振輝 夏鴻斌

(江南大學數字媒體學院 江蘇 無錫 214122)

受益于獨有的可能性聚類特性，較之傳統FCM、k-means等基于類均值方法，PCM擁有更佳的聚類效果和抗噪性能。但PCM為傳統單視角聚類算法，其在面對新興多視角聚類場景時，往往效果欠佳。為解決此問題，基于PCM，提出一種新型的稱為模糊加權多視角可能性聚類WCo-PCM算法。WCo-PCM顯著優點在于其具備對各視角的自適應加權。有關UCI數據集的實驗結果表明該算法較傳統聚類算法及多視角聚類算法更具抗干擾性，有著更佳的聚類性能。

可能性聚類 多視角聚類 模糊加權 抗干擾性

0 引 言

模糊C均值聚類算法(FCM[1-2])是模糊聚類算的鼻祖，它不僅產生較早，且算法簡潔、經典。隨著社會的發展，FCM算法固有的一些缺陷也慢慢凸顯。例如，FCM算法對初始聚類中心敏感、抗干擾性能較差、常會收斂到局部極小值。FCM算法規定各個樣本劃分到各個類的隸屬度之和為1，但這樣的規定對于噪聲點及例外點來說，并不合適。理想狀態下，噪聲點及例外點在劃分的過程中是不應該賦予其一定的隸屬度[3-4]，一旦賦予其隸屬度，則會影響最終的聚類結果。對于該情況，可能性聚類(PCM)算法不再規定各樣本隸屬度之和必須等于1，使得噪聲和例外點在聚類過程中的隸屬度被賦予一個較小值, 從而使其對聚類結果的影響變小，最終增強了聚類算法的抗噪性也提升了算法的聚類性能。然而，傳統的可能性聚類方法無法適應目前新興的應用場景(即多視角模式識別場景)。隨著大數據時代的到來，數據結構呈現復雜化、高維度等特征，多視角數據的出現也如雨后春筍，比較經典的多視角數據集有手寫體數據集、WebKB網頁數據和ORL人臉數據[5]等。多視角數據集能將不同視角的信息有效的結合起來，針對多視角數據進行分析學習能夠更好地把握規律、找準信息。近年來，許多專家學者提出了針對多視角數據進行聚類分析的方法，如Bickel等人提出了多視角聚類算法[6-7]，S.Bickel等人提出了CoEM算法[8]，Cleuziou等人提出了CoFKM算法[9]，文獻[10]將混合模型引入到多視角聚類分析中，從而提出了基于混合模型的多視角聚類算法。傳統多視角聚類算法在具體聚類分析時簡單的認為每個視角提供給聚類分析的貢獻率是一樣的，這并不符合實際情況。因為往往多視角數據中，會出現一個或多個視角的數據的聚類性能優于其他視角，一個或多個視角的聚類性能較差的情況。而將所有視角一視同仁，則會降低優良視角貢獻率，提升較差視角貢獻率，導致無法獲取最好的聚類結果。針對以上情況，本文致力于提出一種新穎的具有視角加權能力的多視角可能性聚類方法。

本文提出的WCo-PCM算法的改進策略主要包含以下兩個方面：(1) 針對傳統的可能性聚類算法無法適應新興的多視角模式識別應用場景，本文提出了基于多視角的可能性聚類算法；(2) 傳統的多視角聚類算法在具體進行聚類分析時，總是會簡單地認為各視角的重要性是相同的。實際上，多視角數據中各個視角數據的聚類性能參差不齊，如若將各個視角數據的重要性一視同仁，那么最終的聚類結果必將受那些具備較差聚類性能的視角所影響而變得不理想。對于這些問題，本文將多視角聚類機制與視角模糊加權機制引入到傳統的PCM算法中，最終形成了模糊加權多視角可能性聚類算法(簡稱WCo-PCM算法)的目標函數式。本文提出的WCo-PCM算法能夠適用在多視角模式識別場景，還可以自適應分配各視角權值，從而提高算法的聚類精度。

1 可能性聚類(PCM)算法

針對FCM算法要求每個樣本屬于所有類的隸屬度之和為1所帶來的弊端，可能性聚類(PCM)算法[11-12]于1993年應運而生。PCM算法不再對隸屬度進行任何限制，直接去除了FCM算法中規定的各樣本屬于每類的隸屬度之和為1的限制。PCM算法賦予了噪聲及例外點較小的隸屬度值， 降低了噪聲及例外點對整個聚類過程的影響，最終增強了算法的聚類性能。

1.1 PCM算法基本原理描述

給定數據集 ，則PCM算法的目標函數式表示如下：

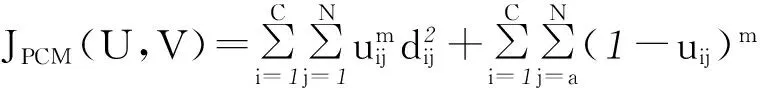
(1)

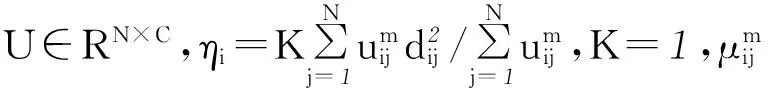
觀察式(1)，PCM算法目標函數式的第一項為FCM算法的目標函數式，其作用是要求所有樣本點到聚類中心的距離值的平方和盡可能小；PCM算法目標函數式的第二項的作用是使隸屬度uij盡可能大，防止某些噪聲點及例外點的隸屬度為整個聚類結果帶來干擾，以增強算法的抗干擾性。

最小化目標函數式(1)，得到最優解時中心點V以及隸屬度U的迭代公式如下：

(2)

(3)

上述兩式均滿足m>1,i=1,2,…,C。由于模糊指數的取值m對聚類結果的影響較大，因此如何確定合適的m值對PCM算法的具體應用至關重要。模糊指數m在聚類分析時的影響主要表現在以下兩方面：(1) 模糊指數m取值越小，則PCM算法越接近于硬劃分HCM算法；(2) 模糊指數m取值越大，得到的空間劃分就越不清楚，類之間的界限就越不清晰，導致最終獲取的聚類結果也不理想。根據文獻[13]給出的參數選取的理論結果，本文m取2。

1.2PCM算法迭代求解過程

結合1.1小節的推導公式，可將PCM算法的聚類過程分為以下步驟：

輸入階段 給定數據集X={x1,x2,…,xN}，參數N表示樣本數據的總數，參數D表示樣本數據的維數。

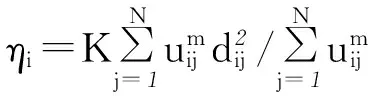
優化迭代階段

Step1 根據式(2)計算新的聚類中心矩陣V(t)；

Step2 結合Step1計算出的聚類中心矩陣V(t)以及已有的隸屬度矩陣U(t)，代入到式(3)求得新的隸屬度矩陣U(t+1)；

Step3 當滿足以下判別條件J(t+1)-J(t)<ε或迭代次數t大于參數M時，算法停止。否則返回Step2進行循環迭代直到滿足任意迭代終止條件。

輸出階段 算法運行結束后，輸出最終的隸屬度矩陣U′以及類中心矩陣V′。

1.3PCM算法亟待改進的問題

隨著時代的發展，算法的應用場景也在不斷變化，傳統PCM算法在當今的模式識別應用場景中還存在一些問題，而這些問題主要體現在以下兩個方面：

問題1 (不適用于新興的多視角模式識別場景)傳統的PCM聚類算法主要針對一些常規樣本進行聚類。所謂常規樣本主要是指那些只從一個角度去描述或度量一個事物的數據，常規數據樣本的呈現的特征一般為：低維、簡單。然而，隨著時代與科技的發展，高維數、結構復雜、分布雜亂的數據集隨即產生并大量出現，多視角數據在這樣的背景下也相繼出現。所謂多視角數據即同一個數據集可從多個角度進行描述或度量，從而獲得多組不同屬性的數據，多組數據結合在一起便形成了對該事物進行全面描述的一個多視角數據集[14]，單、多視角數據對比示意如圖1所示。多視角數據集將所有視角的信息進行了有機結合，結合有效的聚類算法則可以獲得更好的聚類結果。針對多視角數據，傳統的PCM算法應如何進行改進，才能有效聚類并獲得較好的聚類結果。

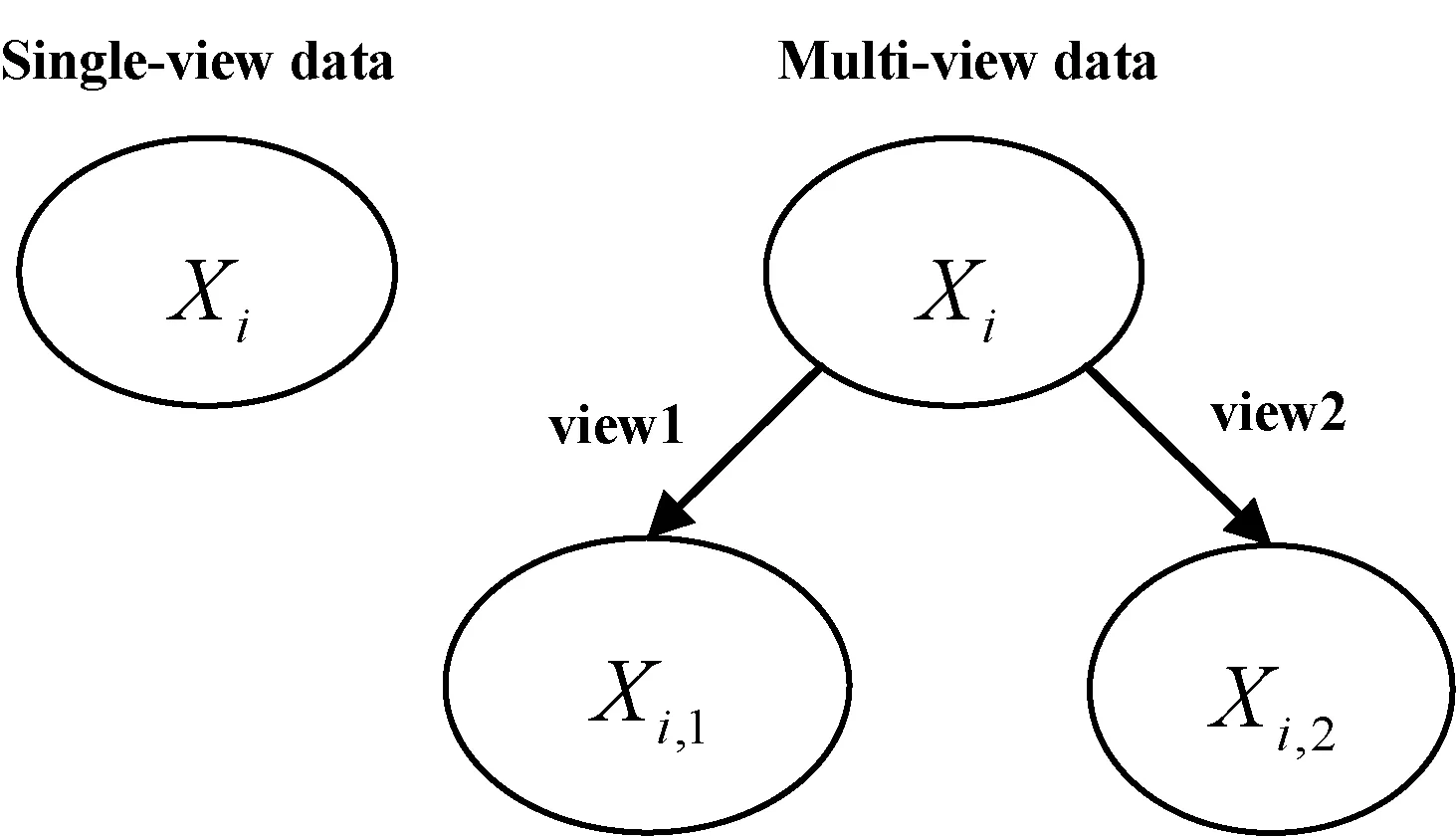
圖1 單、多視角數據對比示意圖

問題2 (各視角的權值默認均分與實際不符) 傳統的多視角聚類算法在具體進行聚類分析時，總是會簡單的認為各視角的重要性是相同的。實際上，多視角數據中各個視角數據的聚類性能參差不齊，如若將各個視角數據一視同仁，那么在最終決策后得到的聚類結果必將被那些具備較差聚類性能的視角所影響，導致最終的聚類結果不理想。針對傳統多視角聚類算法存在的弊端，如何對各視角進行動態加權成為了亟需解決的問題。如圖2所示，第1、2、n-1個視角的聚類效果并不理想，各個類別的數據總存在重疊的情況。而第n個視角的聚類效果則很好，即各個類別的數據距離較遠，不存在重疊的情況。在對各個視角進行加權時，我們很容易想到賦予聚類效果好的視角較大的權值，聚類效果較差的視角較低的權值。

圖2 各視角聚類效果示意圖

2 模糊加權多視角可能性聚類算法

針對1.3小節中提出的兩個問題，以PCM算法作為基礎模型，在本部分將提出本文的主要算法，即具備多視角聚類能力的模糊加權多視角可能性聚類算法WCo-PCM。

2.1 目標函數

首先針對問題1在經典PCM算法上引入多視角協同學習機制使其獲得多視角聚類的能力如下：

(4)

盡管式(4)已使得PCM算法獲得了多視角聚類的能力，但其對于各個視角的權重確是均衡的。這使得該算法仍然會面臨1.3小節中問題2所述之挑戰從而造成最終聚類效果不佳的結果。為了解決此問題，本文進一步在式(4)的基礎上融入視角模糊加權機制，得到了最終的具備視角模糊加權多視角可能性聚類算法(WCo-PCM)目標函數式為：

(5)

其中，各參數需滿足以下的約束條件：

式中，C為聚類的類別總數，N為樣本總數，R為視角總數，α是分歧項占比重系數，uij,r為第r個視角數據的第j個樣本屬于第i個類中心的隸屬度，wr為第r個視角的權值，τ為模糊指數(一般取2)，ηi,r為第r個視角的懲罰因子。

上式所構之WCo-PCM算法不僅具備了多視角協同聚類的能力，同時還可以根據各視角的聚類特性對各視角的聚類結果進行自適應的加權處理，并利用最終獲取的加權結果W=[w1,w2,…,wR]T，進一步使用下式得到具備全局性劃分結果的最終的隸屬度矩陣U′：

(6)

利用式(6)獲取得到的加權意義下的隸屬度矩陣U′，在去模糊后即可獲取較之傳統單視角聚類方法更佳的多視角聚類效果。

2.2 優化迭代參數的相關推導

為了對各參數進行優化學習，本文仿照經典PCM算法的迭代優化策略，仍利用拉格朗日法則，求得目標函數式(5)的最優解，得到聚類中心、隸屬度、視角權值表達式如下：

1) 聚類中心表達式

(7)

2) 隸屬度表達式

(8)

3) 視角權值表達式

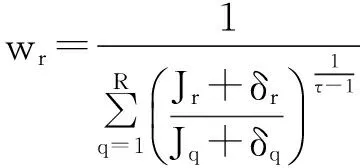
(9)

其中：

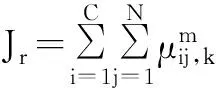
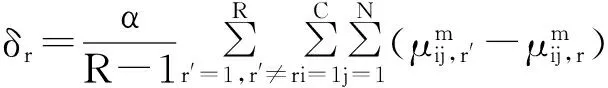
2.3WCo-PCM算法描述

WCo-PCM算法的具體執行步驟如下：

輸入階段 給定數據集X={x1,x2,…,xN}，參數N表示樣本數據的總數。

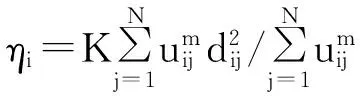
優化迭代階段：

Step1 根據式(7)計算各視角下的新聚類中心矩陣V(t)。

Step2 結合Step1計算出的各視角下的聚類中心矩陣V(t)以及已有的各視角下的隸屬度矩陣U(t)，代入到式(8)求得各視角下的新的隸屬度矩陣U(t+1)。

Step3 當滿足以下迭代終止條件J(t+1)-J(t)<ε或迭代次數t大于參數M時，算法停止。否則返回Step2進行循環迭代直至滿足上述兩項終止條件之一為止。

輸出階段 算法運行結束后，根據式(6)輸出最終的隸屬度矩陣U′,進而根據U′得到最終的聚類結果。

3 實 驗

實驗使用UCI中的多視角數據集對WCo-PCM算法的聚類性能進行分析，評價指標為互信息熵NMI與芮氏指標RI，評價指標詳情如下：

1) 互信息熵[15]

(10)

2) 芮氏指標[15-16]

(11)

NMI與RI的取值范圍均為0到1，兩個指標的取值含義均為取值越大表明算法越優越。本文的實驗環境如下：采用MATLAB2014b，所有試驗在CPU：Corei5，主頻：3.1GHz。內存：4GB的PC上完成。

具體實驗參數設置如下：(1) 最大迭代次數：M=500；(2) 迭代閾值：ε=le-3；(3) 模糊指數：τ=2,m=2；(4) 分歧項所占比例系數α取0.1。

3.1UCI真實數據實驗

為了驗證本算法WCo-PCM對于多視角數據集的聚類性能，本文使用UCI中的手寫體數據集以及圖像分割數據集IS，兩數據集的具體描述如表1所示。本文實驗中的對比算法主要包含兩個方面：

(1) 單視角聚類算法：經典的基于模糊論的FCM算法[4]及經典的基于可能性理論的PCM算法[3]；

(2) 多視角聚類算法：基于模糊C均值算法具備視角間交互式學習能力的多視角模糊聚類CoFKM算法[9]、基于EM模型利用視角間數據分布特性交互學習的CoEM算法[8]、及本文提出的模糊加權多視角可能性聚類算法WCo-PCM算法。

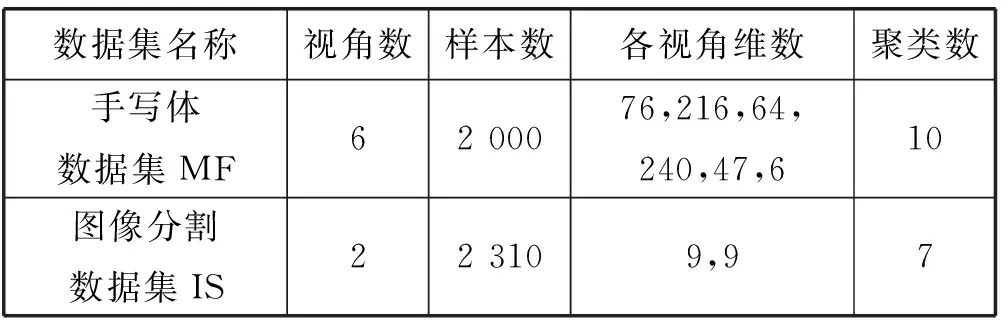
表1 UCI經典數據集描述

表中所有實驗結果均是運行算法20次取均值所得，實驗結果詳見表2所示。

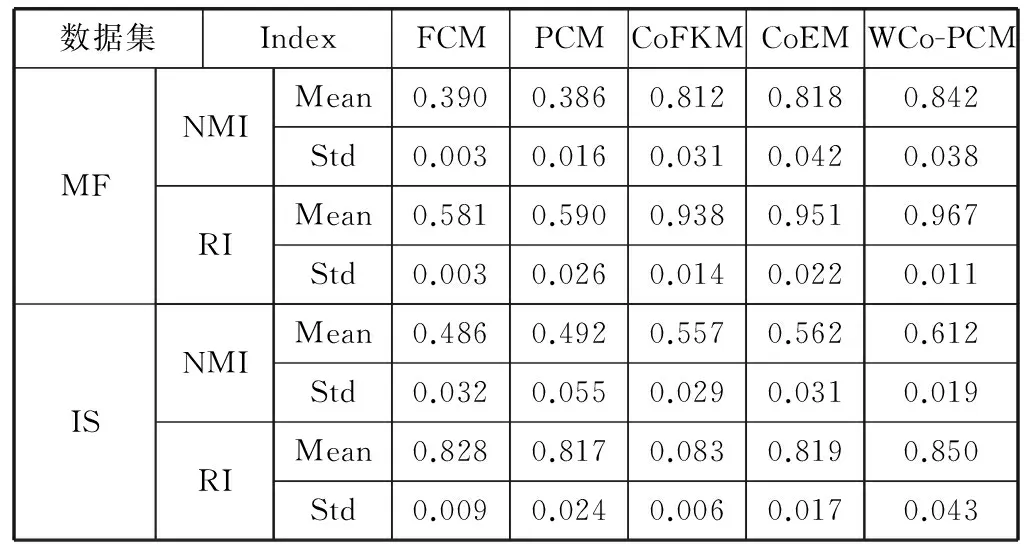
表2 各算法于所含已知信量不同的場景下之性能分析

通過對表2所示實驗結果進行分析，可得出以下結論：(1) 對于多視角數據集，傳統的單視角算法不太適用。如表2所示，無論是MF數據集還是IS數據集，FCM算法以及PCM算法的聚類性能均沒有其他多視角算法的聚類性能好。實驗結果表明，對于多視角數據集的聚類分析，只有用具有多視角聚類分析能力的算法。(2) 本文提出的WCo-PCM算法比其他多視角聚類算法的聚類性能更佳。因為傳統的多視角聚類算法都認為所有視角對聚類分析的重要性是一樣的，而這一情況與實事不符。本算法對每個視角進行了模糊加權，對于具有分歧的視角賦予了較低的權值，最終得到的聚類結果最優。

3.2 比例因子α對聚類性能的影響

WCo-PCM目標函數式里中括號內的第二項為分歧項，該項是用來懲罰那些未達成一致的視角。其中參數α的大小表示分歧項的比重大小，該項的取值對聚類性能的影響本文也做了一定的研究。圖3則為比例因子α在MF、IS數據集中對聚類性能的影響的示意圖。

圖3 比例因子α的變化對聚類性能的影響示意圖

從上面的實驗結果可以看出，當比例因子α取0.1～0.2時，聚類性能最好。

4 結 語

為了使經典的可能性聚類算法能夠更加有效地適用于多視角模式識別場景，本文提出了多視角的可能性聚類算法。傳統的多視角聚類算法在具體進行聚類分析時，總是會簡單地認為各視角的重要性是相同的。實際上，多視角數據中各個視角數據的聚類性能參差不齊，如若將各個視角數據一視同仁，那么在最終決策后得到的聚類結果必將被那些具備較差聚類性能的視角所影響，導致最終的聚類結果不理想。于是本文引入了視角模糊化理論，為各個視角動態賦予了相應的權值。通過在UCI中的多視角數據集MF、IS上進行實驗，其實驗結果均說明本文算法比其他經典的FCM算法、PCM算法、CoFKM算法、CoEM算法方法，不但能夠有效地抵抗噪聲的干擾，而且還能自適應地賦予各個視角一定的權值，提高最終的聚類精度。實驗表明本文提出的模糊加權多視角可能性聚類算法能夠很好地適用于多視角數據集進行聚類。

[1]ZhuL,ChungFL,WangS.Generalizedfuzzyc-meansclusteringalgorithmwithimprovedfuzzypartitions[J].Systems,Man,andCybernetics,PartB:Cybernetics,IEEETransactionson,2009,39(3):578-591.

[2] 朱林,王士同,鄧趙紅.改進模糊劃分的FCM聚類算法的一般化研究[J].計算機研究與發展,2015,46(5):814-822.

[3]PalNR,PalK,KellerJM,etal.Apossibilisticfuzzyc-meansclusteringalgorithm[J].FuzzySystems,IEEETransactionson,2005,13(4):517-530.

[4]BezdekJC.Patternrecognitionwithfuzzyobjectivefunctionalgorithms[M].SpringerScience&BusinessMedia,2013.

[5] 古凌嵐.面向大數據集的有效聚類算法[J].計算機工程與設計,2014,35(6):2183-2187.

[6]BickelS,SchefferT.Multi-ViewClustering[C]//ICDM,2004,4:19-26.

[7]BrefeldU,SchefferT.Co-EMsupportvectorlearning[C]//Proceedingsofthetwenty-firstinternationalconferenceonMachinelearning.ACM,2004:16.

[8]BickelS,SchefferT.EstimationofmixturemodelsusingCo-EM[M].MachineLearning:ECML2005.SpringerBerlinHeidelberg,2005:35-46.

[9]CleuziouG,ExbrayatM,MartinL,etal.CoFKM:Acentralizedmethodformultiple-viewclustering[C]//DataMining,2009.ICDM’09.NinthIEEEInternationalConferenceon.IEEE,2009:752-757.

[10]TzortzisGF,LikasAC.Multipleviewclusteringusingaweightedcombinationofexemplar-basedmixturemodels[J].NeuralNetworks,IEEETransactionson,2010,21(12):1925-1938.

[11]KrishnapuramR,KellerJM.Apossibilisticapproachtoclustering[J].FuzzySystems,IEEETransactionson,1993,1(2):98-110.

[12] 范九倫,裴繼紅.基于可能性分布的聚類有效性[J].電子學報,1998,26(4):113-115.

[13] 宮改云,高新波,伍忠東.FCM聚類算法中模糊加權指數m的優選方法[J].模糊系統與數學,2005,19(1):143-148.

[14] 莊傳志,張道強.多視角判別聚類算法[C]//2009年中國智能自動化會議論文集(第七分冊).南京理工大學學報 (增刊),2009.

[15]DengZ,ChoiKS,ChungFL,etal.Enhancedsoftsubspaceclusteringintegratingwithin-clusterandbetween-clusterinformation[J].PatternRecognition,2010,43(3):767-781.

[16] 洪志令,姜青山,董槐林.模糊聚類中判別聚類有效性的新指標[J].計算機科學,2004,31(10):121-125.

MULTI-VIEW POSSIBILITY CLUSTERING ALGORITHM USING FUZZY WEIGHTING

Wang Zhenhui Xia Hongbin

(SchoolofDigitalMedia,JiangnanUniversity,Wuxi214122,Jiangsu,China)

Benefiting from the delicate mechanism of possibility clustering, PCM appears preferable performance regarding effectiveness and anti-noise, against those conventional mean-based methods such as FCM and k-mean. However, PCM still belongs to the traditional single-view clustering method, which incurs its inefficiency in the fashionable multi-view-oriented scenario. For addressing such challenge, based on PCM, a novel clustering algorithm, referred to as fuzzily weighted multi-view Co-PCM (WCo-PCM for short), is proposed in this paper. The distinctive merit of WCo-PCM lies in its self-adaptive weighting mechanism for the multiple views. The experimental studies implemented on some UCI data sets indicate that, compared with some traditional clustering approaches as well as some existing multi-view ones, WCo-PCM features better anti-interference and clustering effectiveness.

Possibility clustering Multi-view clustering Fuzzy weighting Noise immunity

2016-01-11。江蘇省自然科學基金重點研究專項項目(BK2011003)。王振輝，碩士生，主研領域：人工智能和模式識別。夏鴻斌，副教授。

TP181

A

10.3969/j.issn.1000-386x.2017.04.050