一種面向網絡邊緣任務調度問題的多方向粒子群優化算法
喬楠楠 尤佳莉
(中國科學院聲學研究所國家網絡新媒體工程技術研究中心 北京 100190)
一種面向網絡邊緣任務調度問題的多方向粒子群優化算法
喬楠楠 尤佳莉
(中國科學院聲學研究所國家網絡新媒體工程技術研究中心 北京 100190)
任務調度是云計算及網格計算環境中的重要問題,已有的調度算法往往僅致力于最小化任務的總執行時間而不設置其他約束條件,以致難以實現多種性能指標的同時優化。所提出的面向網絡邊緣任務調度問題的多方向粒子群優化算法,用于解決并發任務在網絡邊緣服務節點中的分布式調度問題,調度的目標是在任務執行的資源開銷不超過閾值的情況下,最小化任務完成的總時間。該方法與現有的離散粒子群優化算法相比同時降低了任務的總完成時間及資源開銷,且在合理預設資源開銷上限的情況下,其計算復雜度實現了較大程度優化。仿真表明,所提出的方法比現有的離散粒子群優化算法的任務總完成時間縮短約10.52%~13.23%,資源開銷減少約10.32%~13.29%。同時,在合理降低資源開銷閾值的情況下,該方法的程序運行時間比現有的粒子群調度方法明顯縮短。
任務調度 多方向粒子群優化 最小化完成時間 開銷閾值
0 引 言
在Web2.0時代,大規模的任務處理需求開始呈現,例如多媒體特效任務、大數據處理任務等。在這些任務場景下,最常見的用戶需求就是實時性需求,也即要求任務能夠被快速響應、快速執行、且執行結果能夠快速回傳給用戶,因此,最小化任務完成時間是任務調度問題中最常見的目標。除此之外,任務調度問題考慮的因素還涉及硬件設備功耗、分布式設備負載均衡度等。
云計算[1]通常通過互聯網來提供動態易擴展的虛擬化的資源,以往的任務調度策略研究也大多是基于云環境展開。在云計算之后,近年來研究者提出了一些基于網絡邊緣環境的分布式計算模型。
Zhu等提出一種新的多媒體云計算框架[2],也即媒體邊緣子云(MEC),將存儲、中央處理單元和圖形處理單元部署在云邊緣位置,以便為各類設備提供分布式并行處理及QoS適配。思科于2011年提出霧計算[3]架構,霧計算是半虛擬化的服務計算架構模型,它更強調網絡邊緣計算設備的作用。在霧計算架構中,服務節點可能是分散在網絡邊緣的零散設備,單個服務節點的計算能力可能較弱,然而依托于特有的低延遲、位置感知特性,這些節點可能提供更具實時性的服務。
以上基于網絡邊緣的分布式計算架構利用網絡邊緣的低延遲特性,為用戶請求提供了實時性響應。本文所討論的任務調度問題,正是基于以下環境特點:
(1) 所有服務節點均分布于網絡邊緣的ISP中,用戶節點位于其中某個ISP。用戶節點及服務節點均具有帶寬感知能力,可以對本節點到其他節點的數據傳輸時延進行預測。
(2) 任務的執行成本采用pay-as-you-go原則進行計算,也即,執行任務所對應的資源開銷與實際的資源用量正相關。
1 現有任務調度算法及存在的問題
任務調度問題是NP-hard問題,已有的任務調度算法主要分為兩大類,一類是基于局部貪心策略的算法[4],另一類是啟發式的智能搜索方法。
在局部貪心策略方面,Max-Min算法用ECT矩陣表示各個任務在各個機器節點上的完成時間的預測值,且每次優先調度具有最長完成時間的作業。Min-Min算法與Max-Min算法計算方式相似,不同之處在于,Min-Min優先調度具有最短完成時間的作業。Sufferage算法用任務在機器上的最早完成時間與次早完成時間差值的絕對值表示為損失度,并優先調度損失度較大的任務。此類基于局部貪心策略的算法,調度的原則是讓當前任務盡可能占用較優的服務器資源,因而可能無法讓所有任務公平地占用資源。
Khaled等提出基于遺傳算法的任務調度方法[5],該算法將一個調度方案表示為一個染色體,并利交叉、變異等運算符實現調度方案的進化。遺傳算法所實現的方案進化是均勻的進化,其收斂速度較慢。
粒子群優化算法(PSO)[6]由Kenney等在1995年提出。PSO算法從隨機解出發,通過適應度函數來評價解的優劣,并通過迭代尋找最優解。相比于遺傳算法,PSO通過追隨當前搜索到的最優值來尋找全局最優解,規則更為簡單,不需要進行交叉和變異等操作。Kenney和Eberhard定義的粒子坐標更新的方式如下所示:
vid=vid+φ(pid-xid)+φ(pgd-xid)
(1)
xid=xid+vid
(2)
其中,d是解空間的一個維度,xi表示粒子群中的第i個粒子,也即第i個解,pi是xi當前在歷次迭代中的獲得的最優解,也即局部最優解,pg則是整個粒子群當前的全局最優解。
由于PSO致力于在連續解空間中進行搜索,對于解決離散解空間中的問題具有局限性。1997年,Kenney等提出了基于離散二進制解空間的粒子群優化算法[7],在該算法中,每一個粒子的坐標都是二進制取值。Kenney等對粒子坐標更新的方式進行了重新定義:
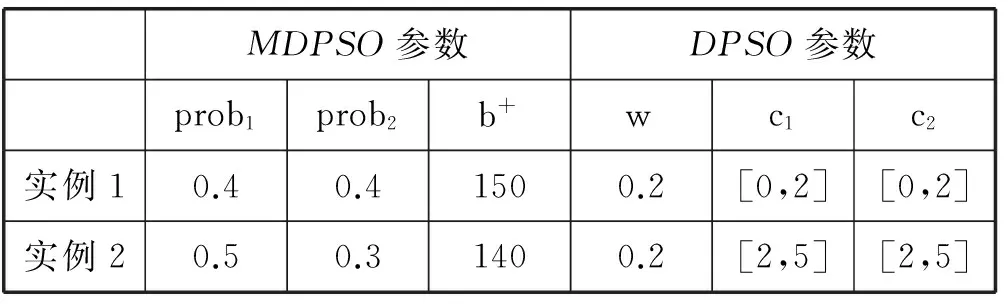
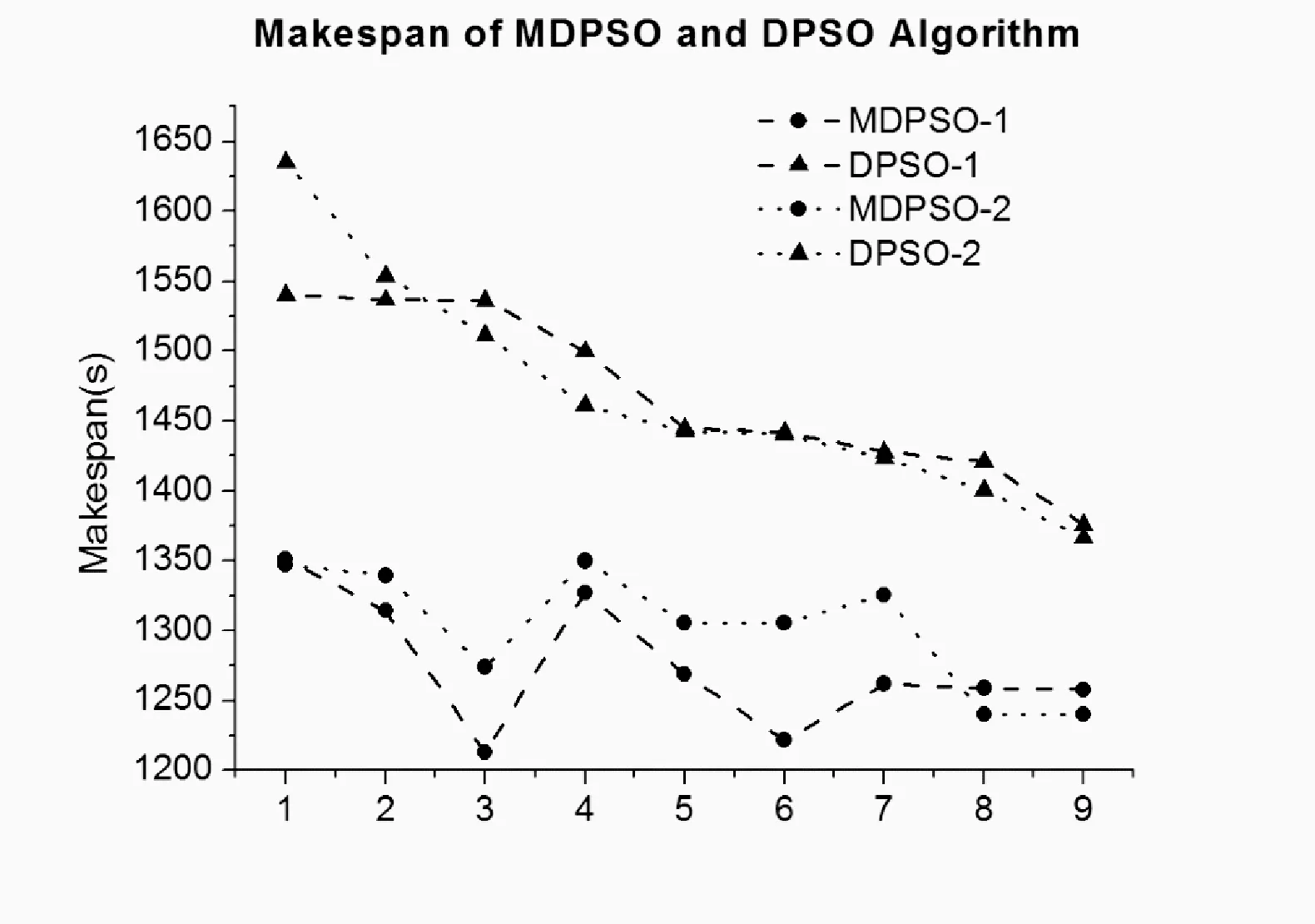
if (rand() (3) 其中S(v) 是Sigmoid函數,如式(4)所示,Sigmoid函數取值與自變量取值呈正相關,其函數值位于區間[0,1]。當S(vid)大于隨機數rand()時,粒子xi在d維的坐標取1,否則取0。 (4) 上述方法有效解決了粒子群在二進制解空間中的粒子坐標編碼問題,通過該方法得出的粒子坐標均為二進制取值。 在此之后,研究者們基于粒子群及離散粒子群優化算法提出了多種任務調度方法,這些方法的優化思路包括粒子坐標編碼[8]、自適應速度調整[9]及局部搜索[10]等。然而現有的基于粒子群優化的任務調度方法仍然存在以下問題: (1) 現有方法大多沿用經典粒子群中的群體遷移思想,即選取全局最優解和局部最優解作為粒子進化的方向。由于局部最優解僅為當前粒子所取得的歷史最優解,并非代表整個群體的最優信息,因此,以局部最優解為導向的進化可能會損失一部分性能; (2) 現有方法中,隨著迭代次數增加,群體中的粒子數目維持恒定,對于在無效解空間中的搜索行為缺少制約條件。 針對上一節中提到的現有粒子群調度算法存在的問題,本節提出一種多方向粒子群優化算法。所提出的算法主要致力于從以下2個方面實現創新及改進: (1) 提出一種新的群體遷移方式。在實際的調度問題中,由于一個粒子實際指代調度問題的一個可行解,也即一個任務分配方案,而非自然界中的個體位置信息,因此粒子的移動無須保持自身的原有軌跡。本文提出的粒子群優化算法,從任務總完成時間(makespan)及資源總開銷(budget)2個維度分別得出精英解集,以2個精英解集為方向實現粒子遷移,使得粒子群同時向makespan優化和budget優化2個方向移動,提供了一種有效的信息共享方法。 (2) 提出基于模糊集合的粒子淘汰機制。該算法制定了基于模糊集合的適應度函數,并根據粒子適應度的優劣進行粒子淘汰,避免了在無效解空間的搜索行為,在一定條件下,可降低程序的計算復雜度。 2.1 問題假設及目標 假設用戶發起N個任務{T1,T2,…,TN},位于網絡邊緣ISP中的M個服務節點{S1,S2,…,SM}提供任務響應及處理。該調度問題基于以下假設: (1) 每個任務可以被任一服務節點執行; (2) 每個服務節點在同一時刻只能處理1個任務; (3) 每個服務節點處理單位大小的源文件所需的時間是已知的; (4) 每個服務節點在工作狀態下單位時間內的資源開銷是已知的; (5) 同一個ISP內部的多個服務節點之間的數據傳輸造成的資源開銷可忽略不計,跨ISP傳輸單位大小文件造成的資源開銷是已知的; (6) 同一個ISP內部的多個服務節點之間的數據傳輸速率大于不同ISP之間的數據傳輸速率。 基于以上假設,調度問題的一個可行解可表示為x=[x(1),x(2),…,x(N)],其中x(i)為第i個任務對應的服務節點ID。該調度問題的目標為:尋找一個任務-服務節點分配矩陣,在任務執行的總開銷不超過預設上限的前提下,最小化任務的總完成時間。 2.2 性能指標計算 根據主流的云計算平臺如AmazonEC2提供的計費機制,用戶因使用彈性資源而支付的費用主要包含兩方面,一方面是占用虛擬機的計算資源及存儲資源所帶來的開銷,另一方面開銷則來自數據傳輸費用。在虛擬機資源計費方面,為適應不同使用場景下的用戶需求,Amazon制定了3種可選使用方式,也即按需使用型實例、預留型實例及即時型實例;在數據傳輸計費方面,數據在同一可用區域之內傳輸不計費,在不同的區域之間視InternetData計費。 在本文所涉及的任務執行成本計算原則上,為詳細分析不同任務調度方法所對應的任務執行開銷,參考Amazon制定的按需使用計費方式,假設單個服務節點的計算成本正比于該節點上任務的完成用時。除此之外,用戶還需支付其向服務節點傳輸任務源文件所造成的數據傳輸費用,此項費用正比于跨區域傳輸的實際數據量。 基于以上原則,用ecti,j表示任務Ti在服務節點Sj上的預測完成時間,bi,j表示Ti在機器Sj上的執行開銷,則ecti,j和bi,j的計算方式如式(5)-式(8)所示: eti,j=ifsi/mipsj (5) sti,j=max(at,itj)+ttr(u,j,ifsi) (6) ecti,j=sti,j+eti,j (7) bi,j=bpsj×eti,j+btr(u,j,ifsi) (8) 其中,eti,j為任務Ti在服務節點Sj上的預測執行用時,ifsi為Ti的源文件大小,mipsj為節點Sj單位時間可處理的源文件大小,sti,j為Ti在Sj上最早開始時間,at為批量任務的到達時間,itj為Sj的最早空閑時間,bpsj為Sj在工作狀態下單位時間內的運行開銷,該取值與Sj的計算能力也即單位時間內的文件處理能力正相關。ttr(u,j,ifsi)為從用戶節點到服務節點Sj傳輸大小為ifsi的文件所需時間,令用戶節點u到服務節點Sj的傳輸速率為bwu,j,則ttr(u,j,ifsi)的計算方式如式(9)所示。btr(u,j,ifsi)為從用戶節點u到Sj傳輸ifsi大小文件所需網絡資源開銷,當u與Sj屬于同一區域ISP時,該項取值為0,否則,令跨區域傳輸單位數據量所需的網絡資源開銷為ξ,則btr(u,j,ifsi)計算方式如式(10)所示。 ttr(u,j,ifsi)=ifsi/bwu,j (9) btr(u,j,ifsi)=ξ×ifsi (10) 對于已知的任務集合{T1,T2,…,TN}及服務節點集合{S1,S2,…,SM},若存在調度問題的一個可行解x=[x(1),x(2),…,x(N)],則該解對應的任務總完成時間makespan(x)及總開銷budget(x)計算方式如下: (1) 將makespan(x)及budget(x)賦值為0; (2) 對于每一個任務Ti,執行步驟(3)-步驟(5); (3) 根據式(3)計算ecti,x(i); (4) 根據式(4)計算bi,x(i),更新budget(x)的值為budget(x)+bi,x(i); (5) 更新服務節點Sx(i)的最早空閑時間; 2.3 粒子群初始化 調度問題的一個可行解稱為一個粒子,在初始化階段,若種群初始規模設置為L,則生成L個隨機粒子x1,x2,…,xL。其中,每一個粒子xi為N維向量,可表示為x=[xi(1),xi(2),…,xi(N)],其中第j維度坐標值xi(j)為第j個任務對應的服務節點ID。 2.4 適應度函數 由于該調度問題的優化目標是在任務執行的總開銷不超過預定閾值b+的情況下,最小化任務的總完成時間,因此設定粒子的適應度值f(x)與其對應的任務總完成時間makespan(x)負相關,即,一個可行解對應的makespan(x)值越大,其適應度越低。同時,對于執行開銷超過閾值的解,對其適應度取值加以限制。 設定任務執行開銷的閾值b+和準閾值b-(b- (11) 如前所述,任務調度的目標是在任務執行的總開銷不超過既定閾值的情況下,最小化任務的總完成時間。因此,適應度函數設定的原則為:當粒子對應的調度方案總執行開銷不超過準閾值b-時,其適應度值與任務的總完成時間成反比,若其總開銷超過b-,則粒子適應度以一定的風險取0,若其總開銷超過閾值b+,則其適應度以100%的概率取0。適應度函數定義如式(12)所示,其中A為式(11)所定義的模糊集合。 (12) 2.5 多方向粒子群進化 2.5.1 基于精英解集的多方向粒子移動 由于一個粒子實際指代調度問題的一個可行解,也即一個任務分配方案,而非自然界中的個體位置信息,因此粒子的移動無須保持自身的原有軌跡。在每一輪迭代中,為保證領導者提供優質的信息,只選取全局最優解作為種群的領導者。 根據2.2節所述的成本計算原則,可以得出makespan和budget兩個性能指標之間的基本關聯:因為節點單位時間內的運行成本與其計算能力正相關,因此,具有較優計算資源的節點在快速處理任務的同時也造成更多資源開銷。但是,makespan與budget兩項指標又在一定程度上存在一致性,由于一個區域ISP內部的數據傳輸不計成本,且傳輸速率大于不同ISP之間的數據傳輸速率,因此,在一定程度上減少跨區域的數據傳輸,可能實現makespan和budget的同時優化。 (1) 將當前粒子群中的所有粒子按照makespan值進行升序排序,并將前K個粒子存放入精英解集Archive1; (2) 將所有粒子按budget值進行升序排序,并將前K個粒子存放入精英解集Archive2; (13) (14) β=[prob1,prob2,1-prob1-prob2] (15) 2.5.2 基于模糊集合的粒子淘汰 為了控制粒子的budget值,使其滿足約束條件,在每一輪迭代中淘汰適應度為0的粒子,從而使群體中保留的粒子均符合約束條件。當滿足下列條件之一時,迭代終止。 (1) 迭代次數超過預設值Max(Iters) (2) 剩余粒子數目小于預設值Min(Population) 粒子群進化算法表示如下所示: Initial the swarm with x1,x2,…,xL; Setthebudgetconstraintb+andb-; Settheprobabilityprob1andprob2; t←1; whiletheterminalconditionisnotmetdo GettheelitesetArchive1andArchive2; fort←1toLdo endfor fort←1toLdo endif endfor L←thecurrentpopulationoftheswarm; t←t+1; endwhile; 上述方法在每一輪迭代中,淘汰適應度為0的解,即,以100%的概率淘汰budget值超過b+的解,并以一定概率淘汰budget值超過b-的解,從而實現對于群體budget的整體控制。 (16) (17) (18) 上述方法提供了適用于本文調度問題的離散坐標編碼方式,從而提供了重現的可能性。同時,該方法與本文具有相似的優化目標,也即致力于優化并發任務的總完成時間,因此本節對上述方法進行重現,并與本文提出的多方向粒子群優化方法進行比較,著重分析任務處理的總時間(makespan)、資源開銷(budget)及程序運行的時間(runtime)。 3.1 測試環境 基于Windows平臺Matlab7.1工具進行了仿真測試,處理器型號為Inteli5-4570,CPU頻率為3.2GHz,可用內存為3.43GB。 3.2 任務規模及服務節點設置 提供服務的14個虛擬機節點VM1-VM14分布在ISP1-ISP3中。CP表示虛擬機節點計算能力,也即節點在單位時間內處理的文件規模(KB/s),BPS表示節點在工作狀態下每秒的開銷(cent/s)。發起任務請求的客戶端建立在ISP2中的VM9節點上,在測試初始化時發起15個任務,任務的源文件規模為32~64MB。如表1所示。 表1 服務節點計算能力及開銷設置 假設一個ISP內部多個節點之間的文件傳輸代價可忽略,跨ISP的文件傳輸開銷與文件大小呈正相關,具體設置如表2所示。同一個ISP內各虛擬機之間傳輸速率為1.25Mbps,不同ISP的虛擬機之間傳輸速率為10Mbps。 表2 各ISP之間文件傳輸開銷設置 3.3 仿真結果及分析 在如下所示2個實例中,精英解集Archive1和Archive2的元素個數均設置為K=5,開銷“準閾值”b-均比b+減少10cent,即b+-b-=10,其余各個參數取值設置如表3所示。 表3 仿真參數設置 在以上2個實例中,針對粒子群初始化規模為200、500、1 000三種情況進行了仿真,且隨著迭代次數的改變,共得出9個數據點P1-P9,如表4所示。 表4 初始化粒子數目及迭代次數設置 在圖1、圖2及圖3中,實例1對應的數據曲線標記為MDPSO-1及DPSO-1,實例2對應的數據曲線標記為MDPSO-2及DPSO-2,橫坐標表示9個數據點P1-P9,仿真結果如下所示。 圖1 Makespan仿真結果 圖2 Budget仿真結果 圖3 Runtime仿真結果 在實例1中,就makespan而言,如圖1所示,MDPSO算法的平均makespan為1 275.2s,相比于DPSO的1 469.7s平均減少 13.23%。就budget而言,如圖2所示,實例1受到閾值b+=150的限制,MDPSO算法的平均budget為144.2cent,相比于DPSO的160.8cent平均減少10.32%。 在實例2中,MDPSO平均實現了1297.5s的makespan,相比于DPSO的1 450.1s降低了10.52%,由于設置了更低的b+值,MDPSO算法實現了更低的budget,MDPSO的budget為138.3cent,相比于DPSO的159.5cent降低了13.29%。 就runtime而言,如圖3所示,由于MDPSO算法涉及全局較優解集合的提取,該步驟具有較高的計算復雜度,在實例1中,隨著粒子數目及迭代次數增加,其runtime逐漸高于DPSO。但在實例2中MDPSO通過合理降低b+值,也即降低budget的上限,可以在每一輪迭代中促使更多無效的解被淘汰,因此粒子的數目明顯減少,在后續的迭代中計算復雜度逐漸降低,runtime明顯低于DPSO。 仿真表明,本文提出的多方向粒子群進化方法具有較好的信息共享能力,通過makespan及budget兩個維度分別獲得全局最優解,實現一種多方向粒子遷移,并使全局最優解的優質的信息以較高的概率保存至新一代粒子群。同時,在適當降低開銷閾值的情況下,算法的計算復雜度得以降低,實現較短的程序運行時間。 本文提出了一種面向網絡邊緣任務調度問題的多方向粒子群優化算法,該方法利用網絡邊緣ISP中的服務節點為終端用戶提交的任務請求提供實時響應,致力于在任務執行的總開銷不超過閾值的前提下,最小化所有任務的總完成時間。一方面,該算法設計了基于精英解集的粒子遷移方法,通過2個全局最優解實現高效的信息共享,使得解空間中的粒子在makespan及budget兩個維度實現同時優化。另一方面,該算法采用基于模糊集合的粒子淘汰方法,在一定條件下降低了算法的計算復雜度。 仿真表明,所提出基于精英解集的粒子遷移方法具有較好的信息共享能力,能夠實現多個目標的同時優化,比現有的離散粒子群優化算法實現的任務總完成時間縮短約10.52%~13.23%,資源開銷減少約10.32%~13.29%。同時,基于模糊集合的粒子淘汰方法,在每一輪迭代中淘汰適應度極低的粒子,在合適的開銷閾值限制下,該方法能夠極大地縮短程序運行的總時間。 [1]ArmbrustM,FoxA,GriffithR,etal.Aviewofcloudcomputing[J].CommunicationsoftheACM,2010,53(4):50-58. [2]ZhuW,LuoC,WangJ,etal.MultimediaCloudComputing[J].IEEESignalProcessingMagazine,2011,28(3):59-69. [3]BonomiF,MilitoR,ZhuJ,etal.FogComputinganditsRoleintheInternetofThings[C]//ProceedingsofthefirsteditionoftheMCCWorkshoponMobileCloudComputing.ACM,2012:13-16. [4]TabakEK,CambazogluBB,AykanatC.ImprovingthePerformanceofIndependentTaskAssignmentHeuristicsMinMin,MaxMinandSufferage[J].IEEETransactionsonParallelandDistributedSystems,2014,25(5):1244-1256. [5]KhaledAKM,TalukderA,KirleyM,etal.MultiobjectivedifferentialevolutionforschedulingworkflowapplicationsonglobalGrids[J].ConcurrencyandComputation:Practice&Experience,2009,21(13):1742-1756. [6]KennedyJ,EberhartR.Particleswarmoptimization[C]//IEEEInternationalConferenceonNeuralNetworks,1995:1942-1948. [7]KennedyJ,EberhartRC.Adiscretebinaryversionoftheparticleswarmalgorithm[C]//IEEEInternationalConferenceonSystems,Man,andCybernetics.IEEE,1997:4104-4108. [8]LiaoCJ,TsengCT,LuarnP.Adiscreteversionofparticleswarmoptimizationforflowshopschedulingproblems[J].Computers&OperationsResearch,2007,34(10):3099-3111. [9]ZuoX,ZhangG,TanW.Self-AdaptiveLearningPSO-BasedDeadlineConstrainedTaskSchedulingforHybridIaaSCloud[J].IEEETransactionsonAutomationScienceandEngineering,2014,11(2):564-573. [10]MoslehiG,MahnamM.AParetoapproachtomulti-objectiveflexiblejob-shopschedulingproblemusingparticleswarmoptimizationandlocalsearch[J].InternationalJournalofProductionEconomics,2011,129(1):14-22. A MULTI-DIRECTIONAL PARTICLE SWARM OPTIMIZATION ALGORITHM FOR NETWORK EDGE TASK SCHEDULING Qiao Nannan You Jiali (NationalNetworkNewMediaEngineeringResearchCenter,InstituteofAcoustics,ChineseAcademyofSciences,Beijing100190,China) Task scheduling is an important problem in cloud computing and grid computing environments. Existing scheduling algorithms are often only dedicated to minimizing the total execution time of tasks without setting other constraints, making it difficult to optimize multiple performance metrics simultaneously. The proposed multi-directional particle swarm optimization algorithm for network edge task scheduling problem solves the distributed scheduling problem of concurrent tasks in network edge service nodes. The goal of scheduling is to minimize the total time of task completion in the case that the resource cost of task execution less than the threshold. Compared with the existing discrete particle swarm optimization algorithm, this method reduces the total task completion time and resource cost, and achieves a large degree of optimization of its computational complexity in the case of a reasonable preset resource overhead. The simulation results show that compared with the existing discrete particle swarm optimization algorithm, this method can reduce the total task completion time by about 10.52%~13.23% and the resource cost by 10.32% ~13.29%. Meanwhile, the running time of this method is significantly shorter than that of the existing discrete particle swarm optimization algorithm in the case of a reasonable reduction of resource overhead threshold. Task scheduling Multi-direction particle swarm optimization Minimal makespan Overhead threshold 2016-03-16。中國科學院戰略先導技術專項基金(XDA06040501)。喬楠楠,碩士生,主研領域:優化算法,多媒體服務。尤佳莉,副研究員。 TP3 A 10.3969/j.issn.1000-386x.2017.04.0532 多方向粒子群優化算法解決任務調度問題
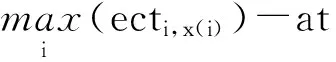
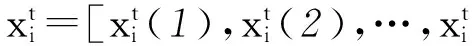
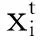



3 仿真測試
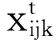
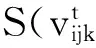





4 結 語

