基于統計方法的CPU內電壓傳感器布局綜述

劉曉晨

（1.中國科學院 上海微系統與信息技術研究所，上海200050；2.上海科技大學 上海200031；3.中國科學院大學 北京100049）

基于統計方法的CPU內電壓傳感器布局綜述

劉曉晨1，2，3

（1.中國科學院 上海微系統與信息技術研究所，上海200050；2.上海科技大學 上海200031；3.中國科學院大學 北京100049）

針對如何使用電壓傳感器監測CPU芯片供電網絡內電壓緊急狀態發生狀況這一核心問題，介紹和對比了兩種最新的研究成果：基于統計概率計算框架的傳感器布局方案和基于統計學習Group Lasso算法的傳感器布局方案。前者選擇最容易發生電壓緊急狀態的節點用于放置傳感器，后者則通過對供電網絡內各節點電壓的線性關系施以正則化的方法來選擇線性預測模型中最重要的節點用于放置傳感器。通過分析兩種方法的異同和各自的適用場景，指出了布局問題未來與機器學習相結合的發展方向。

電壓緊急狀態；傳感器布局；概率框架；機器學習

隨著集成電路產業的快速發展和處理器芯片集成度的大幅提升，中央處理器芯片（CPU）供電網絡內的電壓噪聲逐漸成為了影響其穩定工作的重要原因。當晶體管的供電電壓下降到安全工作的閾值電壓Vth以下時，晶體管處于不穩定的亞閾值狀態，有可能導致功能模塊電路（如ALU、Fetch Unit等）的計算錯誤。這種供電電壓Vdd低于安全工作閾值電壓Vth的現象又被稱為電壓緊急狀態（Voltage Emergency）。集成電路新技術的發展使得電壓緊急狀態的出現概率大幅提升：一方面，出于功耗控制的考慮，芯片的Vdd被不斷降低，同時晶體管特征尺寸的縮減也使得Vth不斷降低，然而Vdd的下降速度遠快于Vth的下降速度，以至于晶體管安全工作的電壓余裕（Safe Margin）被大幅縮減；另一方面，時鐘門控技術（Clock Gating）、電源門控技術（Power Gating）及動態電壓頻率調節技術（DVFS）等CPU低功耗技術的采用使得部分電路的Vdd在瞬時內產生大幅變化。由于供電網絡是一個具有容性和抗性的RLC網絡，因此某一區域Vdd的瞬時變化會使得供電網絡內其他區域隨之產生震蕩，從而影響這些區域的供電穩定性，并有很大概率引發電壓緊急狀態。

在實際的工業設計和生產中，為了避免電壓緊急狀態帶來的工作錯誤，電壓傳感器模塊常被放置在芯片中，用于監測供電網絡的Vdd變化情況，并在電壓緊急狀態發生前采取一定的措施。目前對于相關措施研究所取得的成果主要集中在兩個方面：1）根據大量仿真及實驗中取得的Vdd變化數據，學習電壓緊急狀態發生前Vdd的變化趨勢，并在Vdd實際變化趨勢與學習數據相符合時，提前做出預判，提升部分區域的Vdd，或重新分配任務使模塊使用率下降[1-4]。2）允許電壓緊急狀態的發生，在Vdd降低到Vth前保存現有電路狀態，待電壓緊急狀態結束后采取回滾機制（Rollback Mechanism），恢復到電壓緊急狀態發生前的電路狀態，繼續工作[5-8]。

綜上，不管采用何種方法，芯片內必須采用電壓傳感器提供Vdd信息。傳統的方法是在Vdd變化最劇烈的電路模塊區域內直接放置傳感器。然而在實際情況中，為了保持電路模塊的完整性、避免過高的設計代價，電壓傳感器通常都會放置在電路模塊外圍具有足夠空間的空白區域內。因此，傳感器在空白區域內的布局優化問題便隨之而生。簡而言之，傳感器的布局主要解決兩個問題：1）在芯片空白區域內放置多少個傳感器？位置在哪里？2）如何更好地利用傳感器得到的電壓信息？

針對以上問題，密蘇里科學技術大學的Tao Wang等人于2013年提出了一個基于概率框架的解決方案—“Eagle-Eye”[9]，該方法利用芯片SPICE仿真獲得的各節點供電電壓波形及概率計算，尋找最適合放置電壓傳感器的節點位置。另一種方法由中國科學院上海微系統與信息技術研究所的Xiaochen Liu等人于2015年提出[10]，該方法利用統計學習方法中的Group Lasso算法，尋找芯片空白備選區域中對芯片全局電壓預測最重要的若干位置，并基于仿真數據進一步建立了電路模塊內部波動最惡劣節點（hotspot）實際電壓的預測模型。本文綜述了這兩種解決方案的所采用的統計學習方法和實驗結果，對兩種方法在適用條件和場景兩方面做出了比較。

1 CPU供電網絡數學模型

CPU供電網絡是一個多層網格狀網絡，最上層電網與提供穩定Vdd和GND的球狀觸點相接觸。下層電網與芯片內的各個晶體管直接相連。電壓傳感器可直接測量下層晶體管處得到的Vdd，這些允許被測量的位置被稱為電壓節點（Node）。由于供電電網采用的導線自身具有一定的阻抗和寄生電感，且晶體管也具有一定的電容特性，因此整個網絡可被視為一個復雜的RLC網絡。這使得最上層提供的穩定Vdd在向下層傳輸的過程中存在損耗，并具有伴隨激勵而產生一定震蕩的特點。對供電網絡的仿真實驗可獲得各個節點的Vdd電壓波形，其中一部分節點處在芯片功能電路模塊外，并具有一定空間用來放置電壓傳感器，而另一部分節點則處在電路模塊內部，其Vdd只能通過仿真得到，并不具備通過傳感器直接測量的條件。假設芯片上有K個功能電路模塊，每個模塊內存在一個電壓波動情況最劇烈，最能反映模塊電壓狀況的節點（hotspot），則在總計N個采樣周期內的任意一個采樣時刻n，每個hotspot的Vdd電壓都可以用（k=1，2，…，K；n=1，2，…，N）表示。同樣地，我們也可以用（m=1，2，…，M；n=1，2，…，N）表示在n時刻每個傳感器候選節點 （可放置傳感器的節點，共M個）的Vdd電壓。總而言之，仿真中得到的所有hotspot和傳感器候選節點的Vdd電壓分別可用兩個矩陣F和X表示，所有節點的電壓可用矩陣Z表示[11]：

2 研究方法

基于上述CPU供電電網抽象數學模型，以下將詳細介紹兩種方案的模型構造數學實現。

2.1 基于概率框架的布局解決方案

密蘇里科學技術大學的Tao Wang等人提出的“Eagle-Eye”是一個建立在概率框架上的解決方案。記隨機變量，即Z矩陣的其中一行。則我們可以定義一個指標——遺漏率（miss rate），來衡量某一種布局下對電壓緊急狀態報告的遺漏情況：

在上式中，Zmin是所有R個節點中最小的Vdd電壓值，t是晶體管安全工作的閾值電壓Vth，在芯片上放置S個電壓傳感器，是用來放置傳感器的這S個節點的Vdd電壓值。此式的含義為：在芯片上總計R個電壓節點中，選出S個用于放置電壓傳感器，并基于這些電壓傳感器讀取到的Vdd電壓值來判斷芯片供電網絡內是否有電壓緊急狀態（Vdd小于t）發生。當時，所有電壓傳感器讀取的Vdd電壓值均未小于t，系統認為此時芯片處于安全供電狀態。然而在這種情況下，如果Zmin≤t，那么芯片上必然有一個電壓節點的Vdd電壓值低于安全閾值t，也就意味著此時芯片上發生了電壓緊急狀態，但沒有被傳感器報告。根據貝葉斯公式，上式可簡化為：

由于P（Zmin≥t）只與電路自身的設計情況有關，與傳感器的布局無關，可看作為常量。因此，傳感器布局問題等價于一個最小化布局遺漏率 （miss rate）的優化問題，即選出哪S個電壓節點放置傳感器，使得電壓緊急狀態沒有被報告的遺漏率最低：

輸入：芯片上所有電壓節點的集合R={1，…，R}，傳感器數量S和閾值電壓t。

輸出：用于放置傳感器的電壓節點集合S={r1，…，rs}?R。

1：集合S=?，SQM（S）=∞

2：循環i=1：S

3：選擇k∈R，使SQM（S∪k）最小

4：R=R/k

5：S=S∪k

6：結束循環

該算法共有S次循環，每次循環中計算SQM的次數為R，因此該算法的復雜度為。

基于SPICE仿真得到的結果顯示（見圖1，Ⅰ，Ⅱ，Ⅲ三條數據線分別表示理想Vdd=1.8 V時分別為1.71 V、1.713 V和1.715 V時遺漏率隨放置傳感器數量的變化趨勢）：1）隨著選擇放置傳感器節點數量的增加，電壓緊急狀態的遺漏率顯著降低，并在數量大于5之后趨于穩定；2）隨著增大，電壓緊急狀態的判斷條件更為嚴格，在使用相同數量傳感器 （小于5）時遺漏率也隨之下降。

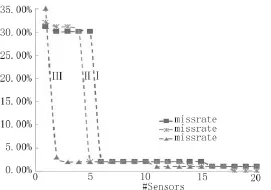
圖1 傳感器數量與遺漏率的關系

2.2 基于Group Lasso算法的布局解決方案

中國科學院上海微系統與信息技術研究所的Xiaochen Liu等人提出了基于統計學習和機器學習方法中Group Lasso算法的解決方案。該方案的基本假設是各模塊hotspot節點Vdd電壓與傳感器候選節點電壓之間的線性可預測關系，即：

每一個模塊內的hotspot節點Vdd電壓值可由所有傳感器候選節點Vdd的電壓值線性表示，系數矩陣α中每一個元素αk，m表示第m個候選節點用于線性預測第k個模塊hotspot節點時的系數，矩陣C為線性預測的誤差項。因此，基于普通最小二乘法可求得矩陣α及用所有M個候選節點電壓預測某一模塊hotspot節點電壓的線性關系表達式。然而，傳感器布局問題要求使用較少量而非全部的電壓傳感器，因此問題關鍵在于如何選出S個傳感器用于布局。基于以上要求，該方法引入Group Lasso算法[14-15]，對原最小二乘問題施以正則化方法。對矩陣F和X中每一列分別進行歸一化后，生成矩陣F′和X′，則Group Lasso算法求解以下問題：

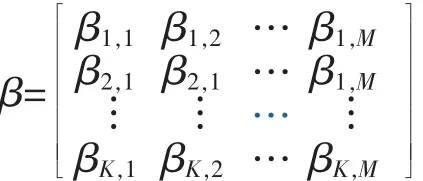
其中‖β2‖2表示系數矩陣β第m列向量的二范數，λ（λ＞0）是一個用戶自定義值的懲罰參數。由該式可知，矩陣β中的每一列βm都對應一個傳感器候選節點，該列各元素的值代表用于預測各個模塊hotspot節點電壓時的系數。因此，二范數‖β2‖2可以表征第m個候選節點處電壓值對于預測芯片上所有hotspot節點電壓的作用程度，也即重要性大小。若‖β1‖2＞‖β2‖2，則可認為在預測中第一個候選節點的重要性要強于第二個候選節點。更進一步，若人為設定一個參考值T，所有滿足‖βm‖2＞T的候選節點都可被選擇為放置傳感器的位置。此外，λ對于如何選擇候選節點有著十分重要的作用。λ對各個候選節點的二范數‖βm‖2值直接做出限制：當λ較小時，大部分‖βm‖2接近于0；隨λ著逐漸增大，越來越多的‖βm‖2值會超過T；當λ趨于無窮大時，該問題等價于普通最小二乘法問題。基于仿真得到的結果所示（見圖2），當λ=10時，兩百個傳感器候選節點中絕大部分‖βm‖2處于10-5至10-10，而當λ增大至30時，對‖βm‖2的整體懲罰逐漸減輕，‖βm‖2的值變大，且有一些已跳出10-5至10-10的范圍，接近于1。若我們假設T=10-3，則被選出放置傳感器的節點數量由2增長至7。由此可見，λ是選擇候選節點的主要工具，通過改變其值可觀察各個候選節點‖βm‖2的變化，從而根據其大小決定哪些節點用于放置傳感器。

圖2 各候選節點二范數值與λ的關系

在選出S個候選節點后，我們需要解決布局的第二個問題：如何應用傳感器讀取的電壓值？假設選出的S個候選節點集合S={r1，…，rs}，則這些位置上傳感器所讀取到的電壓值仍可以用矩陣Xs表示（Xs是矩陣X的行子矩陣）。因此我們可以重新求解以下最小二乘問題，建立各個模塊hotspot節點電壓與傳感器讀取電壓之間的線性關系表達式：

設該問題的最優解為 αS*，則第 k個模塊內hotspot節點電壓與傳感器電壓讀數之間的關系為：

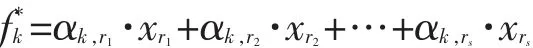
因此，我們在以上線性模型的基礎上，可以直接利用傳感器讀取的電壓值，來預測每個模塊內hotspot節點電壓，從而精確判斷該模塊位置是否發生電壓緊急狀態。實驗結果顯示，通過調節λ值的大小，該方法能夠有效選擇不同數量的候選節點，當使用的傳感器數量增多時，模塊hotspot電壓的預測值與真實值之間的相對誤差逐漸減小。

圖3 λ值、預測相對誤差及傳感器數量關系

3 結束語

文中詳細介紹了兩種用于監測電壓緊急狀態的傳感器布局方案。第一種方案“Eagle-Eye”適用于使用只能報告電壓是否低于一定值的簡單二元輸出電壓傳感器的情況。該方法通過仿真結果和概率計算框架選擇放置傳感器的位置，并基于傳感器報告的電壓狀況簡單判斷芯片上是否有電壓緊急狀態發生。其優勢在于反映速度快，使用的傳感器結構簡單。然而，這種方法并不能準確判斷具體哪個模塊或位置出現了電壓緊急狀態，無法有針對性地對局部供電網絡采取適當措施避免或修正電壓緊急狀態所帶來的負面影響。

第二種方案需使用能夠測得連續電壓值的傳感器，利用統計學習方法中的Group Lasso算法選擇放置傳感器的位置，并基于傳感器讀取的電壓值線性預測各個模塊的電壓狀態。由于連續值電壓傳感器結構較復雜，第二種方案物理實現的成本也相對較高。但該方法能夠獲得未放置傳感器節點的準確電壓值，因此可與其他需要準確電壓值來提供后續處理的供電網絡調節策略相結合，以達到更精準的調節效果。綜上所述，兩種方案有各自不同的應用方向，CPU芯片設計者可根據自身需求靈活采用，對電壓緊急狀態做出判斷。也由此可見，未來傳感器布局問題的發展方向將由傳統的直接測量向基于大量仿真數據的機器學習方向逐漸轉變。

[1]Reddi V J，Gupta M S，Holloway G，et al.Voltage emergency prediction:Using signatures to reduce operating margins[C]//High Performance Computer Architecture，2009.HPCA 2009.IEEE 15th International Symposium on.IEEE，2009:18-29.

[2]Joseph R， Brooks D， Martonosi M.Control techniques to eliminate voltage emergencies in high performance processors[C]//High-Performance Computer Architecture，2003.HPCA-9 2003. Proceedings.The 9th International Symposium on. IEEE，2003:79-90.

[3]Lefurgy C R，Drake A J，Floyd M S，et al.Active guardband management in power7+to save energy and maintain reliability[J].Micro，IEEE，2013，33（4）:35-45.

[4]Gupta M S，Reddi V J，Holloway G，et al.An event-guided approach to reducing voltage noise in processors[C]//Proceedings of the Conference on Design，Automation and Test in Europe.European Design and Automation Association，2009:160-165.

[5]Tschanz J，Bowman K，Lu S L，et al.A 45nm resilient and adaptive microprocessor core for dynamic variation tolerance[C]//2010 IEEE International Solid-State Circuits Conference-（ISSCC）. 2010.

[6]Gupta M S，Rangan K K，Smith M D，et al. décor:A delayed commit and rollback mechanism for handling inductive noise in processor[C]//High Performance Computer Architecture，2008.HPCA 2008.IEEE 14th International Symposium on. IEEE，2008:381-392.

[7]Mack M，Sauer W M，Swaney S B，et al.IBM POWER6 reliability[J].IBM Journal of Research and Development，2007，51（6）:763-774.

[8]Ernst D，Kim NS，Das S，et al.Razor:A lowpower pipeline based on circuit-level timing speculation[C]//Microarchitecture，2003.MICRO-36.Proceedings.36th Annual IEEE/ACM International Symposium on.IEEE，2003:7-18.

[9]Wang T，Zhang C，Xiong J，et al.Eagle-eye:a near-optimal statistical framework for noise sensor placement[C]//Computer-Aided Design（ICCAD），2013 IEEE/ACM International Conference on. IEEE，2013:437-443.

[10]Liu X，Sun S，Zhou P，et al.A statistical methodology for noise sensor placement and full-chip voltage map generation [C]//Proceedings of the 52nd Annual Design Automation Conference. ACM，2015:94.

[11]Enami T，Ninomiya S，Hashimoto M.Statistical timing analysis considering spatially and temporally correlated dynamic power supply noise [J].Computer-Aided Design of Integrated Circuit and Systems，IEEE Transaction on，2009，28（4）: 541-553.

[12]Visweswariah C，Ravindran K，Kalafala K，et al. First-order incremental block-based statistical timing analysis [J].Computer-Aided Design of Integrated Circuit and Systems，IEEE Transaction on，2006，25（10）:2170-2180.

[13]Cheng L，Xiong J，He L.Non-Gaussian statistical timing analysis using second-order polynomial fitting[J].Computer-Aided Design of Integrated Circuit and Systems，IEEE Transaction on，2009，28（1）:130-140.

[14]Guyon I，Elisseeff A.An introduction to variable and feature selection[J].The Journal of Machine Learning Research，2003，3:1157-1182.

[15]Yuan M，Lin Y.Model selection and estimation in regression with grouped variables[J].Journal of the Royal Statistical Society:Series B （Statistical Methodology），2006，68（1）:49-67.

Two statistical approaches for voltage sensor allocation in CPU

LIU Xiao-chen1，2，3
（1.Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，Shanghai 200050，China；2.School of Information Science and Technology，ShanghaiTech University，Shanghai 200031，China；3.University of Chinese Academy of Sciences，Beijing 100049，China）

Based on the core problem of allocating voltage sensors to monitor voltage emergencies in power delivery network of CPU chips，this paper introduces and compares two novel and state-of-theart approaches.One sensor allocation approach employs a statistical probability framework to find nodes where voltage emergencies most likely to happen.The other approach applies Group Lasso algorithm on the linear system of voltages in power delivery network to select important predictors （sensor locations）. By comparing these two approaches in methodology and application，this paper reveals the trend of introducing machine learning into allocation optimization problem.

voltage emergency；sensor allocation；probability framework；machine learning

TN0

：A

：1674-6236（2017）08-0092-05

2016-03-17稿件編號：201603224

劉曉晨（1990—），男，遼寧撫順人，碩士研究生。研究方向：計算機輔助設計（CAD）。