一類廣義Jacobi矩陣的逆特征值問題

孟純軍,姜婷婷

(湖南大學數學與計量經濟學院，中國 長沙 410082)

一類廣義Jacobi矩陣的逆特征值問題

孟純軍,姜婷婷

(湖南大學數學與計量經濟學院，中國 長沙 410082)

本文研究了一類廣義Jacobi矩陣的逆特征值問題，給出了該問題有解的充要條件，并討論了解的唯一性.進一步，本文給出算法計算該問題的解，數值實例說明算法是行之有效的.

Jacobi矩陣;廣義Jacobi矩陣;特征值;逆特征值問題

矩陣的逆特征值問題來源很廣泛，如自動控制、系統識別、主成份分析、遙感、分子頻譜分析、量子物理等[1].在數學物理問題中，根據給定系統的方程式和定解條件求系統的變化狀態稱為正問題；另一方面，給出方程的解，求方程的系數及邊界條件，稱為數學物理反問題.著名的Sturm-Liouville問題的反問題就是利用特征值或特征函數來確定Sturm-Liouville方程的系數及邊界條件.Sturm-Liouville反問題離散化可歸納為一類Jacobi矩陣特征值反問題[2].彈簧-質點系統的振動模型中，若已知振動系統的全部固有頻率及其他一些子系統的結構特征，來確定該模型中的物理參數質量mi和彈性系數ki，稱為彈簧-質點模型振動反問題，這類問題也可歸結于Jacobi矩陣的逆特征值問題[3-4].

Jacobi矩陣是特殊的對稱三對角矩陣，要求其副對角線元素全為正.因為Jacobi矩陣的來源非常廣泛，其特征值具有嚴格隔離的良好特點[5],其逆特征值問題一直是數值代數的研究熱點.較早研究Jacobi矩陣的逆特征值問題是Hald[6].他研究的問題為： 給定實數λ1<λ2<…<λn，及μ1<μ2<…<μn-1，求一個Jacobi矩陣Jn,使得Jn的特征值為λ1,λ2,…,λn，并且Jn的n-1階順序主子陣的特征值為μ1,μ2,…,μn-1.文獻[6]中給出了有解的條件及解的個數，求解的算法，但該算法當n(n≥35)比較大時誤差很大.Boor 和Golub在文獻[7]繼續研究該問題，并提出了新的算法，進一步提高了算法的精度.

本文繼續研究Hald所提出的問題，著重研究求解該問題的算法，并將Jacobi矩陣進行推廣，即如下類型的廣義Jacobi矩陣：

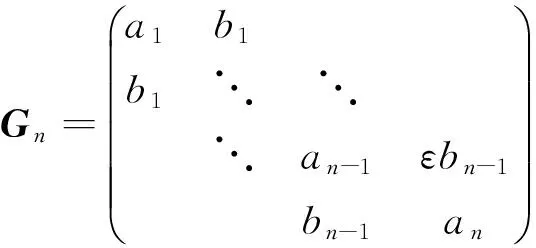
(1)

其中bi>0，(i=1,2,…,n-1),ε>0.當ε=1時，Gn為Jacobi矩陣.本文著重研究計算廣義Jacobi矩陣逆特征值問題的算法，該算法也能計算Hald研究的問題.數值實例表明算法是有效的.我們還將本文的算法與Boor和Golub文獻[7]中的算法進行比較，數值實例說明本文的算法更有效，精度更高.

本文研究的問題具體描述如下：

問題：給定2n-1個實數λ1<λ2<…<λn和μ1<μ2<…<μn-1,以及正實數ε，構造一個形如(1)的n階廣義Jacobi矩陣Gn，使得λ1,λ2,…,λn為Gn的特征值，μ1,μ2,…,μn-1為其n-1階順序主子陣Jn-1的特征值.

具體內容安排如下：在第二部分討論問題有解的條件以及解的唯一性，得到有解的充要條件.在第三部分討論計算問題解的算法，并給出了兩個數值實例.數值實驗表明，與文獻[6]和[7]的算法比較，本文的算法精度更高，可行性更好.

1 解的存在唯一性

引理1[5]若λ1,λ2,…,λn為n階Jacobi矩陣Jn的特征值，μ1,μ2,…,μn-1為其對應的n-1階順序主子陣的特征值，則λi<μi<λi+1,(i=1,2,…,n-1)(嚴格隔離性)

引理2[6]設給定2n-1個實數λ1<λ2<…<λn和μ1<μ2<…<μn-1滿足λj<μj<λj+1,(j=1,2,…,n-1)，則存在唯一的n階Jacobi矩陣Jn,使得λ1,λ2,…,λn為Jn的特征值，μ1,μ2,…,μn-1為其n-1階順序主子陣Jn-1的特征值.

定理 給定2n-1個實數λ1<λ2<…<λn和μ1<μ2<…<μn-1,以及正實數ε，則存在形如(1)的廣義Jacobi矩陣Gn，使得λ1,λ2,…,λn為Gn的特征值，μ1,μ2,…,μn-1為其n-1階順序主子陣Jn-1的特征值的充要條件為λj<μj<λj+1,(j=1,2,…,n-1).并且，這樣的廣義Jacobi矩陣Gn是唯一的.

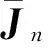
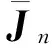
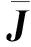
ai(i=1,2,…,n)，bj(j=1,2,…,n-1)，εbn-1，

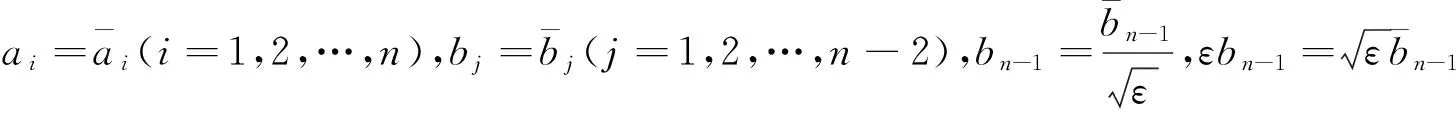
2 數值算法

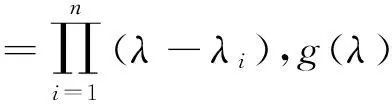
其中h(λ)為其n-2次多項式，則

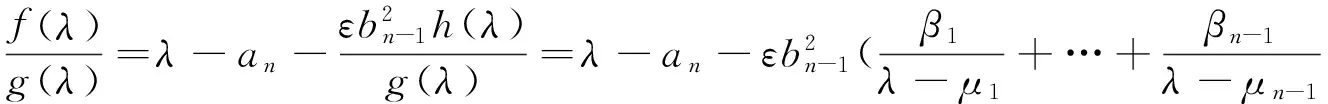
(2)

由留數定理可得，

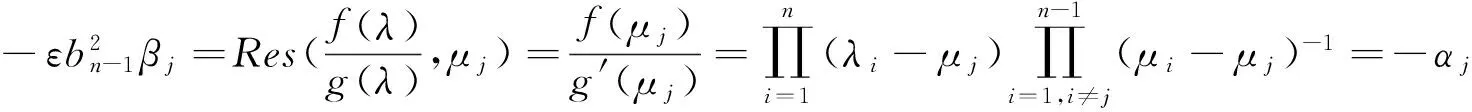
(3)

由嚴格隔離條件λj<μj<λj+1,(j=1,2,…,n-1)，容易驗證，αj>0,(j=1,2,…,n-1).

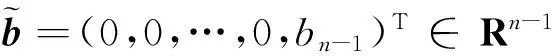
其中

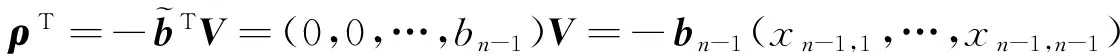
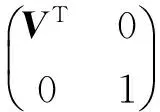
由文獻[8]可知，

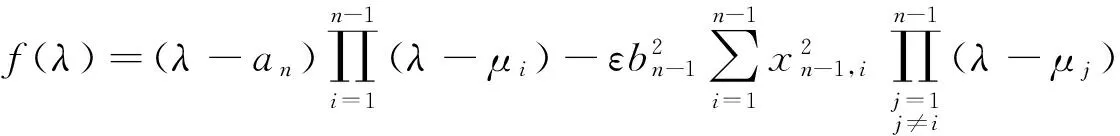
所以

(4)

由特征值與矩陣跡的關系，可知：

(5)

由式(2)，(3)和(4)，及αj>0,(j=1,2,…,n-1)，得

(6)

(7)

(8)

由式(6)和(7)可得

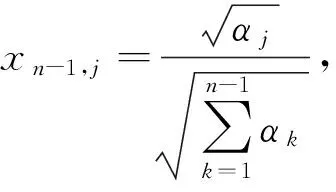
(9)

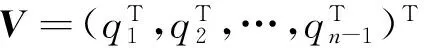
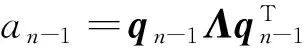
(10)

從而

bn-2=‖qn-1Λ-an-1qn-1‖2

(11)

qn-2=(qn-1Λ-an-1qn-1)/bn-2

(12)

這里，‖·‖2指的是歐幾里得范數，同理可得an-2,…,a1，bn-3,…,b1,從而得到所求的滿足條件的廣義Jacobi矩陣Gn.

綜上所述，可得到如下算法.

算法.

輸入2n-1個實數λ1<λ2<…<λn和μ1<μ2<…<μn-1，以及正實數ε；

Step 1. 檢查是否滿足嚴格隔離性，λj<μj<λj+1,(j=1,2,…,n-1)，若成立，接step 2, 若不成立，該逆特征值問題無解；

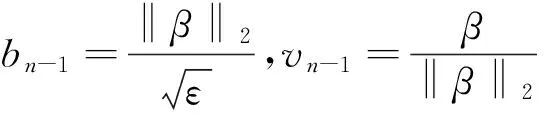
Step 4. 令向量vn=0,Λ=diag(μ1,μ2,…,μn-1)，

Fori=n-1:-1:2

qi-1=viΛ-aivi-bivi+1;

bi-1=‖qi-1‖2;

End

3 數值實例

例1 給定11個實數如下：

λ1=-3,λ2=-2,λ3=1,λ4=3,λ5=4,λ6=6

μ1=-2.5,μ2=-1,μ3=2,μ4=3.5,μ5=5

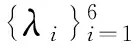
解 應用上述算法，通過Matlab編程計算得到矩陣,

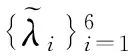
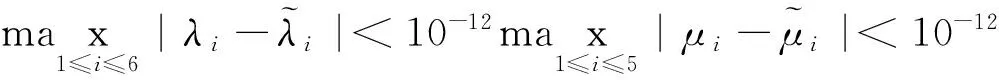
算例表明，所計算得到的廣義Jacobi矩陣較好的滿足了所給的特征值條件，因此算法是有效的.

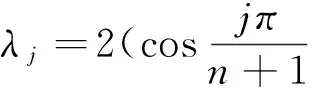
當n分別為25,50,100,200時，用本文的算法(ε=1)來求這個n階Jacobi矩陣，并與文獻[7]的結果進行比較.

解 應用上述算法，即ε=1時，通過Matlab編程計算得到n階Jacobi矩陣的元素，并與精確的Jacobi矩陣對角線元素及第二對角線元素-2和1進行最大誤差分析，結果如表1所示.

表1 數值結果

算例表明，本文的算法比文獻[7]的算法精度高.

[1] CHU M T. Inverse eigenvalue problems[J].SIAM Rev,1998,40(1):1-39.

[2] 鄧遠北.幾類線性矩陣方程的解與PROCRUSTES問題[D].長沙：湖南大學，2003.

[3] 周樹荃，戴 華.代數特征值反問題[M].鄭州：河南科學技術出版社，1991.

[4] PETER N, FRANK U. Inverse eigenvalue problems associated with spring-mass systems[J].Linear Algeb Appl, 1997,254(1):409-425.

[5] J.H.戈盧布，C.F.范洛恩. 矩陣計算(中譯本，袁亞湘等譯)[M]. 北京：科學出版社, 2001.

[6] HALD O H. Inverse eigenvalue problems for Jacobi matrices[J]. Linear Algeb Appl,1976,14(1):63-85.

[7] BOOR C D, GOLUB G H. The numerically stable reconstruction of a Jacobi matrix from spectral data[J]. Linear Algeb Appl,1978,21(3):245-260.

[8] 鐘 璨.對稱箭形矩陣的逆特征值問題[D].長沙:湖南大學，2007.

(編輯 HWJ)

A Class of Inverse Eigenvalue Problems for the Generalized Jacobi Matrix

MENGChun-jun*,JIANGTing-ting

(College of Mathematics and Econometrics, Hunan University, Changsha 410082, China)

In this paper we considered a class of inverse eigenvalue problems for the generalized Jacobi matrix. The necessary and sufficient conditions under which the problem is solvable are presented. Their uniqueness is also discussed. Furthermore, we provided an algorithm to obtain the solution. Numerical examples were given to illustrate that our algorithm is both feasible and effective.

Jacobi matrix; generalized Jacobi matrix; eigenvalues; inverse eigenvalue problem

10.7612/j.issn.1000-2537.2017.02.012

2016-01-08

國家自然科學基金資助項目(11271117)

O241.6

A

1000-2537(2017)02-0076-05

*通訊作者,E-mail：mengchunjun@hnu.edu.cn