LED圓形陣列照度峰值的冪函數擬合研究

劉 沁,劉啟能

(1.重慶工商大學 設計藝術學院，重慶 400067；2.重慶工商大學 計算機科學與信息工程學院，重慶 400067)

LED圓形陣列照度峰值的冪函數擬合研究

劉 沁1,劉啟能2

(1.重慶工商大學 設計藝術學院，重慶 400067；2.重慶工商大學 計算機科學與信息工程學院，重慶 400067)

利用LED照度公式推導出LED圓形陣列光斑的照度峰值公式，建立了研究LED圓形陣列光斑照度特性的數值計算方法。在此基礎上利用擬合方法得出了LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑變化的冪函數公式, 這些冪函數擬合公式能夠很好地與數值計算結果吻合。利用這些公式能夠十分方便地對LED圓形陣列光斑的照度峰值特性進行解析研究，為了研究LED圓形陣列光斑的照度峰值特性建立了一種新方法，彌補了數值計算方法和仿真軟件不能對LED圓形陣列光斑的照度峰值特性進行解析研究的缺陷。

發光二極管；圓形陣列；照度峰值；擬合方法；冪函數

引言

LED作為一種新型光源，由于其壽命長、發光效率高已被廣泛地應用于各種照明環境，包括大屏幕顯示、背光源、汽車和特種照明燈等等。因此在理論上對LED照明特性的研究也越來越受到業內人士的關注[1-5]。文獻[6][7]研究了通過自由曲面來重新配光實現LED光源的均勻照明。文獻[8]研究了利用自由曲面透鏡來實現LED光源的大視場角準直照明。但由于受生產工藝和生產技術的限制，單個LED芯片的功率較小，產生的照度不強，因此限制了單個LED芯片在多數照明領域的應用。為了解決單個LED芯片照度不足的問題，可將多個LED芯片組成LED 陣列用于滿足不同照明需要[9-11]的情況。 在LED 陣列中最為典型的是LED圓形陣列和LED方形陣列，文獻[12]和文獻[13]分別利用粒子群算法和全局優化算法研究了LED圓形陣列和LED方形陣列照度的均勻性問題，得出了LED圓形陣列和LED方形陣列照度的均勻度與陣列結構參數的關系。

關于LED陣列照度特性的研究是一個重要的問題，但目前研究LED陣列照度特性的主要方法是通過數值計算法或仿真軟件的計算來得到LED陣列的照度變化特征。而數值計算法和仿真軟件只能通過有限的數據點或圖形來反映LED陣列的照度隨自變量的變化特征，它們不能直接反映出LED陣列的照度隨自變量的函數變化規律。因此數值計算法或仿真軟件不便對LED陣列照度隨自變量的變化規律進行深入的解析分析和研究。由此可見，在理論上建立LED陣列的照度隨自變量的函數關系對研究LED陣列的照度規律是十分重要的。為了在理論上解決這一問題，本文將利用單個LED芯片的照度公式推導出LED圓形陣列的照度公式，建立研究LED圓形陣列的照度數值計算方法。在此基礎上利用擬合方法得出LED圓形陣列的照度峰值隨目標距離、芯片光強以及陣列半徑變化的冪函數公式。這一問題的解決為研究LED圓形陣列光斑的照度特性建立了一種新方法，彌補了數值計算方法和仿真軟件不能對LED圓形陣列光斑的照度特性進行解析研究的缺陷。

1 模型與理論

單個LED芯片發出的光強I與視角θ滿足下列關系[14]：

其中I0為視角為0方向的光強，m值由半角θ1/2決定(半角θ1/2是指光強降為中心光強一半時所對應的視角)。m值與半角θ1/2的關系為

設單個LED芯片在點(X，Y,0)處，目標平面上的照明點P在(x,y,h)處，如圖1所示。則單個LED芯片在P點處產生的照度E與光強I滿足余弦定律[15]：

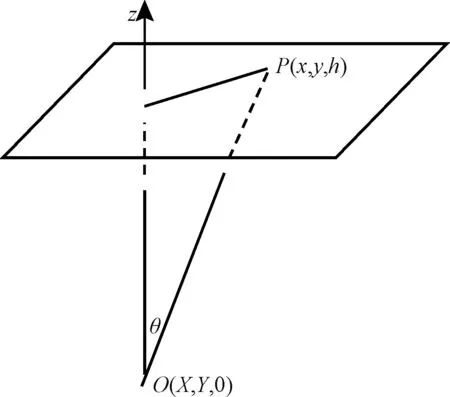
圖1 單個LED芯片的照度Fig.1 A single chip of illuminance

(3)

式(3)中的l為芯片到P點距離。由式(1)和式(3)可得單個LED芯片在P點處產生的照度為

如果在平面z=0上有N個LED芯片，則在P點處產生的照度為

式(5)中Xn、Yn為第n個LED芯片的坐標。

設計這樣一種LED圓形陣列，它由M個等距圓周構成，每個圓周上均勻分布12個LED芯片，相鄰兩個圓周的間距為d，最小一個圓周距圓心的距離為d，圓形陣列的半徑r=Md。該LED圓形陣列的LED芯片數N=12×M。圓形陣列在z=0平面內，其圓心的坐標在(0,0,0)處，x軸和y軸分別與一組徑向芯片重合。目標平面為z=h,如圖2所示。由于該LED圓形陣列以Z軸為對稱軸，所以該LED圓形陣列在目標平面產生的照度分布也是以Z軸為對稱軸。由式(5)可得該LED圓形陣列在目標平面上P點(x,y,h)產生的照度為

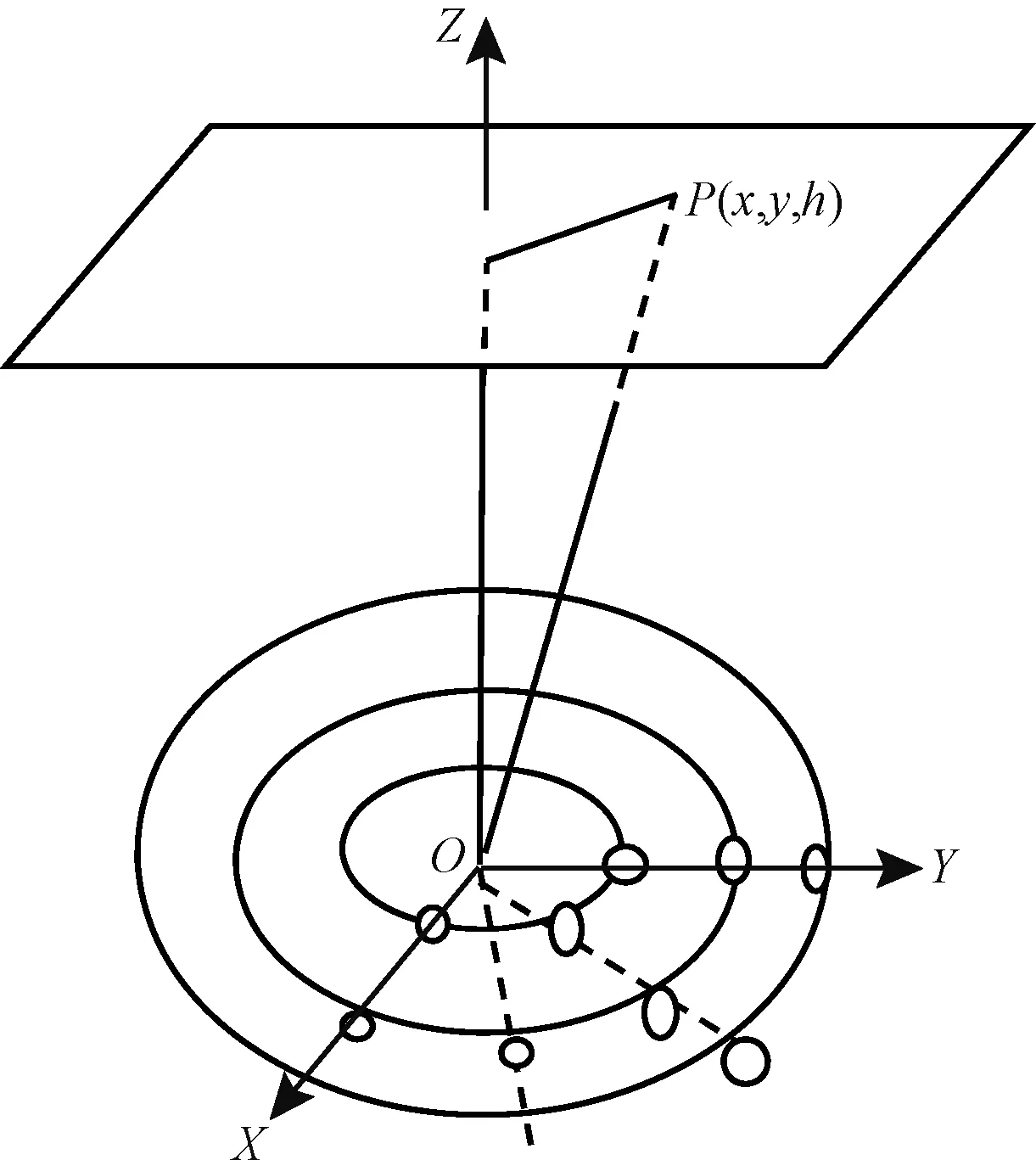
圖2 LED圓形陣列的照度Fig.2 LED circular array of illumination

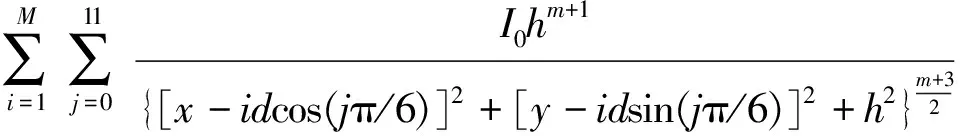
利用式(6)可以研究LED圓形陣列在目標平面上光斑的照度規律。由對稱性可知光斑的照度峰值出現在目標平面上的(0,0,h)處，由式(6)可得光斑的照度峰值E0滿足

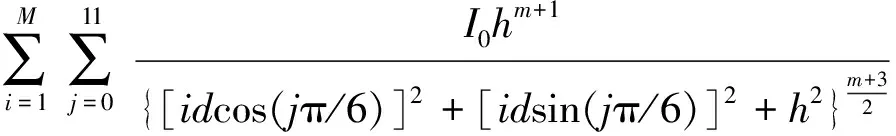
由式(7)可知LED圓形陣列光斑的照度峰值由目標距離、芯片光強以及陣列半徑決定。由式(7)通過數值計算可以得出LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑的變化特征。

而式(7)是數值計算公式，它只能通過數值計算得出的一系列數據來反映LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑的變化特征，而不能得出照度光斑峰值隨目標距離、芯片光強以及陣列半徑的函數變化規律。因此式(7)給出的數值計算方法無法對LED圓形陣列光斑的照度峰值進行解析分析和研究。為了彌補數值計算方法的不足，有必要利用函數擬合方法來找出LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑的函數變化規律。

通過對LED圓形陣列光斑的照度峰值的變化特征進行冪函數擬合、指數函數擬合、三角函數擬合的試探后發現：冪函數擬合不僅函數關系簡單，而且能夠很好地與數值計算法得到的結果吻合。下面就介紹LED圓形陣列光斑的照度峰值的冪函數擬合方法。通過大量的試探和比較研究發現，LED圓形陣列光斑的照度峰值的變化規律可以用冪函數表示：

其中x為自變量(它可以為目標距離h、芯片光強或陣列半徑r中的任何一個，x選不同的量。式(8)就反映照度光斑峰值隨該量的變化規律)。β為擬合變量，通過調整β的大小使式(8)給出的函數曲線與數值計算法得到的數據吻合來確定β的值，具體方法是利用最小二乘法得到最優擬合變量β。b和c為待定系數，由數值計算法得到的初點x1、E01和末點xl、E0l的數據確定，其確定方法是將x1、E01和xl、E0l代入式(8)，解出b和c為：

將式(8)和式(9)稱為LED圓形陣列光斑的照度峰值的冪函數擬合法。該方法能夠得到光斑的照度峰值的函數變化規律，它彌補了數值計算方法和仿真軟件的不足。

由式(8)還可以得到照度峰值與自變量的反函數關系：

式(10)在LED圓形陣列的照明設計中有重要的應用，通過式(10)可以十分方便地計算出不同照度峰值下的目標距離、芯片光強或陣列半徑的值，為LED圓形陣列的照明設計提供理論數據。

2 照度峰值的特性

下面利用數值計算法式(6)、式(7)和冪函數擬合法式(8)～式(10)來研究LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑的變化規律。

2.1 照度峰值與目標距離的關系

取陣列的芯片總數N=12×10、單個芯片的I0=5 cd、陣列半徑r=0.6 m,固定m=30。利用數值計算法式(6)可以計算出目標距離為2 m、5 m、8 m時所對應的光斑照度在目標平面上x軸上的分布曲線，如圖3所示。由圖3可知：光斑的范圍隨目標距離增加而逐漸增大，光斑的照度峰值隨目標距離增加而迅速減小。由于光斑的照度峰值直接影響LED圓形陣列的照明效果，因此得到照度峰值隨目標距離的函數變化規律是十分重要的。

為了得到照度峰值隨目標距離的函數變化規，利用數值計算法式(7)計算出目標距離為2 m、3 m、4 m、5 m、6 m、7 m、8 m、9 m時對應光斑的照度峰值E0列在表1中。

表1 目標距離h及對應的光斑照度峰值E0Table 1 The value of h and E0

圖3 光斑照度隨x的響應曲線Fig.3 Response curves of intensity of illumination versus x

將表1中目標距離所對應的光斑照度峰值E0的8組數據，畫在圖4中，為8個黑圓點。再將目標距離h和照度峰值E0的初點(h1=2 m、E01=94.777 lx)和末點(hl=9 m、E0l=7.203 5 lx)代入式(9)，確定對應的待定系數b和c：

將b和c代入(9)式得光斑的照度峰值E0隨目標距離h的擬合冪函數關系：

E0=bhβ+c

該式中光斑的照度峰值E0不僅是目標距離h的函數，而且E0還受擬合變量β的調制。利用最小二乘法得到最優擬合變量β=-1.397。將β=-1.397代入上述兩式得光斑的照度峰值隨目標距離的冪函數變化規律：

將式(11)光斑的照度峰值E0隨目標距離h的函數關系繪在圖4中(實線)，它能很好地通過8個數值計算點。并且計算出該擬合冪函數與數值計算結果的平均相對誤差為1.02 %。這表明擬合冪函數與數值計算結果吻合得很好。式(11)就是用冪函數擬合方法得到的LED圓形陣列光斑的照度峰值E0隨目標距離h的函數變化規律，通過它能夠清晰地反映出光斑的照度峰值E0隨目標距離h的函數變化關系，便于對光斑的照度峰值E0隨目標距離h的變化規律進行解析研究，這是數值計算方法和仿真軟件不能實現的。

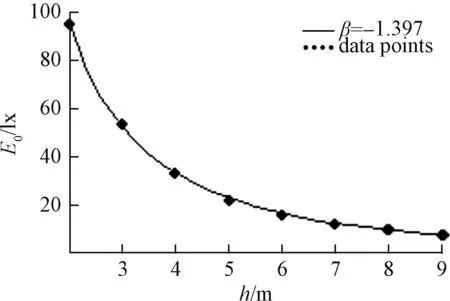
圖4 照度峰值隨目標距離的響應曲線Fig.4 Response curves of the peak of intensity illumination versus target distance

另外由式(11)可以得到目標距離隨照度峰值的函數變化規律：

(12)

在照明設計中由式(12)可以方便地計算出當E0=30 lx時其對應的目標距離為4.23 m，當E0=5lx時其對應的目標距離為10.4m，為LED圓形陣列的照明設計提供理論數據。這是仿真軟件難以得到的。

2.2 峰值與芯片光強的冪函數關系

仍取陣列的芯片總數N=12×10、m=30，固定目標距離h=2 m、陣列半徑r=0.6。利用數值計算法式(6)可以計算出單個芯片的光強I0為2cd、3.5cd、5cd時其對應的光斑照度在目標平面上x軸上的分布曲線，如圖5所示。圖5可知：光斑的照度峰值隨單個芯片的光強增加而增大，光斑的范圍隨單個芯片的光強增加而無明顯變化。由于光斑的照度峰值直接影響LED圓形陣列的照明效果，因此得到照度峰值隨單個芯片光強的函數變化規律是十分重要的。

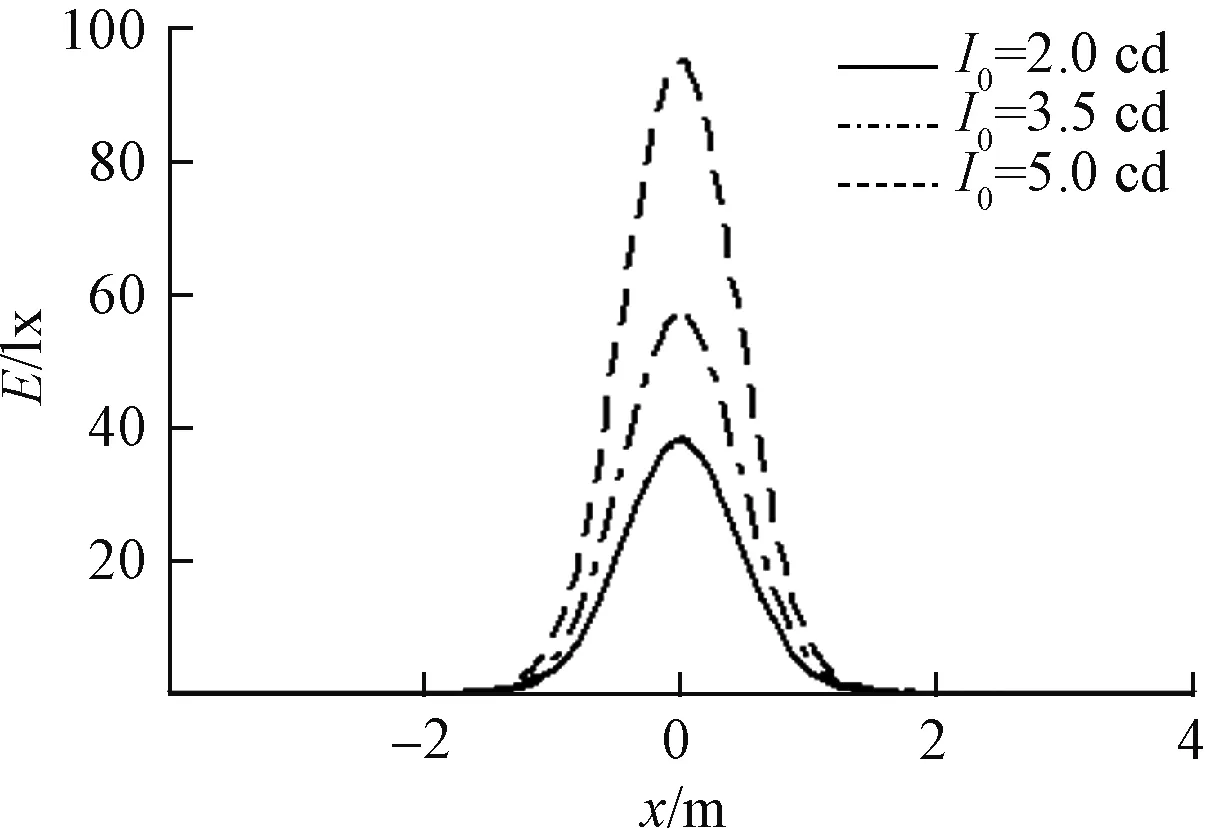
圖5 光斑照度隨x的響應曲線Fig.5 Response curves of intensity of illumination versus x

為了得到照度峰值隨單個芯片光強的函數變化規，利用數值計算法式(7)計算出陣計算出單個芯片的光強I0為2cd、2.5cd、3cd、3.5cd、4cd、4.5cd、5cd、5.5cd時對應的光斑的照度峰值E0列在表2中。

表2 芯片的光強I0和對應的光斑點照度峰值E0Table 2 The value of I0 and E0

利用表2中照度峰值的數據和最小二乘法能夠得到照度峰值隨單個芯片光強的擬合冪函數變化規律。利用最小二乘法得到最優擬合變量β=1.000。將β=1.000代入式(8)和式(9)得照度峰值隨單個芯片光強的冪函數變化規律：

將式(13)照度峰值隨芯片光強的函數關系繪在圖6中(實線)，它能很好地通過8個數值計算點。并且計算出該擬合冪函數與數值計算結果的平均相對誤差為0.004%。這表明擬合冪函數與數值計算結果吻合得很好。

另外由式(13)可以得到芯片光強隨照度峰值的函數變化規律：

在照明設計中由式(14)可以方便地計算出要使目標距離h=2 m處的照度峰值E0達到110lx，必須選擇芯片光強I0=5.8cd。要使目標距離h=2 m處的照度峰值E0達到130lx，必須選擇芯片光強I0=6.9 cd，為LED圓形陣列的照明設計提供理論數據。這也是仿真軟件難以得到的。

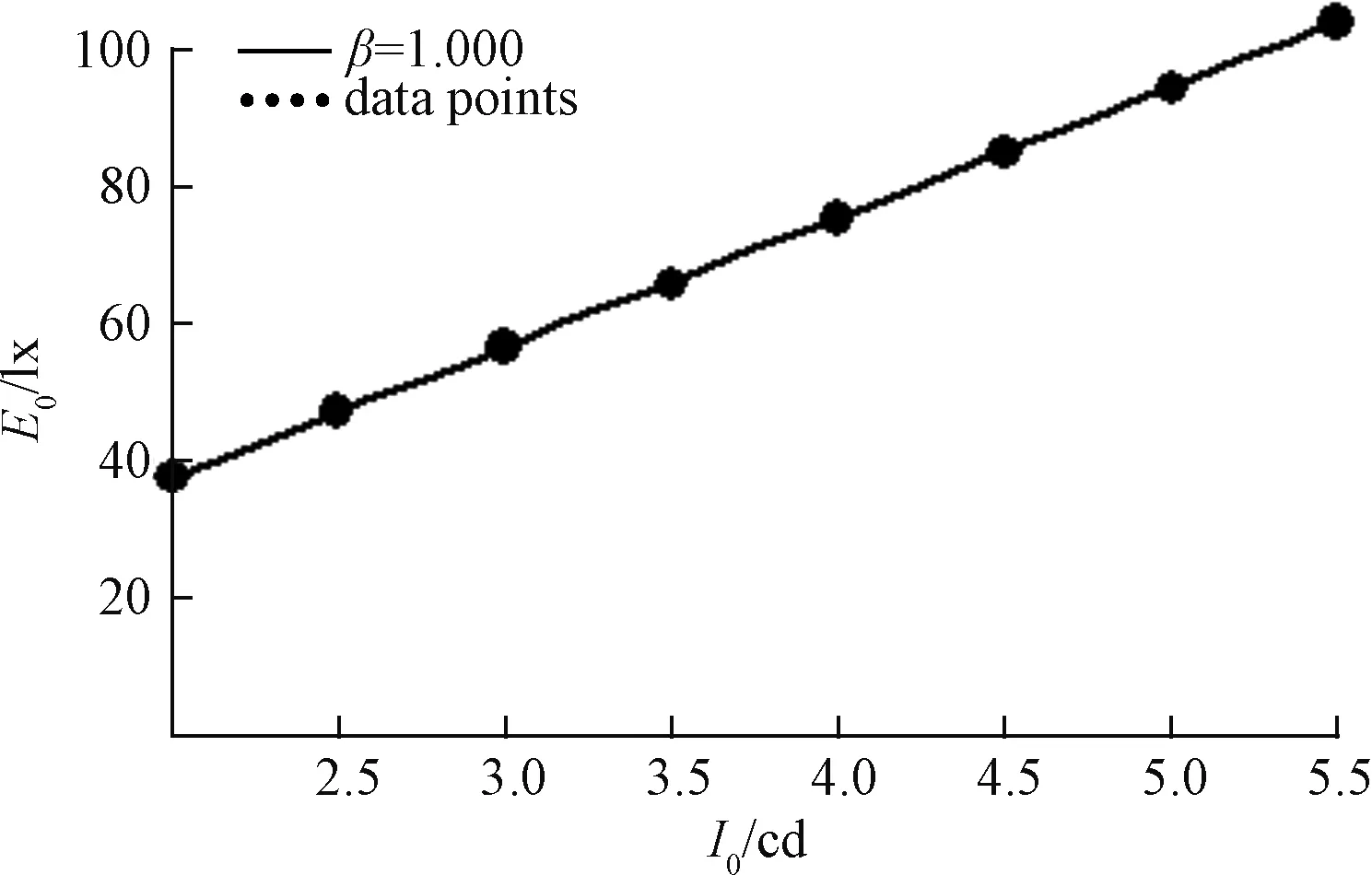
圖6 照度峰值隨芯片光強的響應曲線Fig.6 Response curves of the peak of intensity illumination versus chip light intensity

2.3 照度峰值與陣列半徑的關系

仍取陣列的芯片總數N=12×10、單個芯片的I0=5 cd，固定目標距離h=3 m、m=30。利用數值計算法式(6)可以計算出陣列半徑r為0.2 m、0.8 m、1.4 m時其對應的光斑照度在目標平面上x軸上的分布曲線，如圖7所示。圖7可知：光斑的范圍隨陣列半徑增加而逐漸增大，光斑的照度峰值隨陣列半徑增加而逐漸減小。由于光斑的照度峰值直接影響LED圓形陣列的照明效果，因此得到照度峰值隨陣列半徑的函數變化規律是十分重要的。

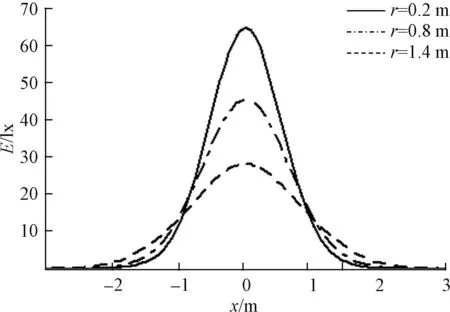
圖7 光斑照度隨x的響應曲線Fig.7 Response curves of intensity of illumination versus x

為了得到照度峰值隨陣列半徑的函數變化規，利用數值計算法式(7)計算出陣列半徑r為0.2 m、0.4 m、0.6 m、0.8 m、1.0 m、1.2 m、1.4 m、1.6 m時對應的光斑的照度峰值E0列在表3中。

利用表3中照度峰值的數據和最小二乘法能夠得到照度峰值隨陣列半徑的擬合冪函數變化規律。利用最小二乘法得到最優擬合變量β=0.799。將β=0.799代入式(8)和式(9)得照度峰值隨陣列半徑的冪函數變化規律：

將式(15)照度峰值隨陣列半徑的函數關系繪在圖8中(實線)，它能較好地通過8個數值計算點。并且計算出該擬合冪函數與數值計算結果的平均相對誤差為1.4%。這表明擬合冪函數與數值計算結果吻合得較好。利用式(15)能夠十分方便地研究LED圓形陣列的照度峰值隨陣列半徑的變化規律。

表3 陣列半徑r與照度峰值E0Table 3 The value of r and E0

另外由式(15)可以得到陣列半徑隨照度峰值的函數變化規律：

在照明設計中由式(16)可以方便地計算出要使目標距離h=3 m處的照度峰值E0得到20 lx，必須使陣列半徑=1.81 m。要使目標距離h=3 m處的照度峰值E0為30 lx，必須使陣列半徑=1.39 m，為LED圓形陣列的照明設計提供理論數據。這也是仿真軟件難以得到的。

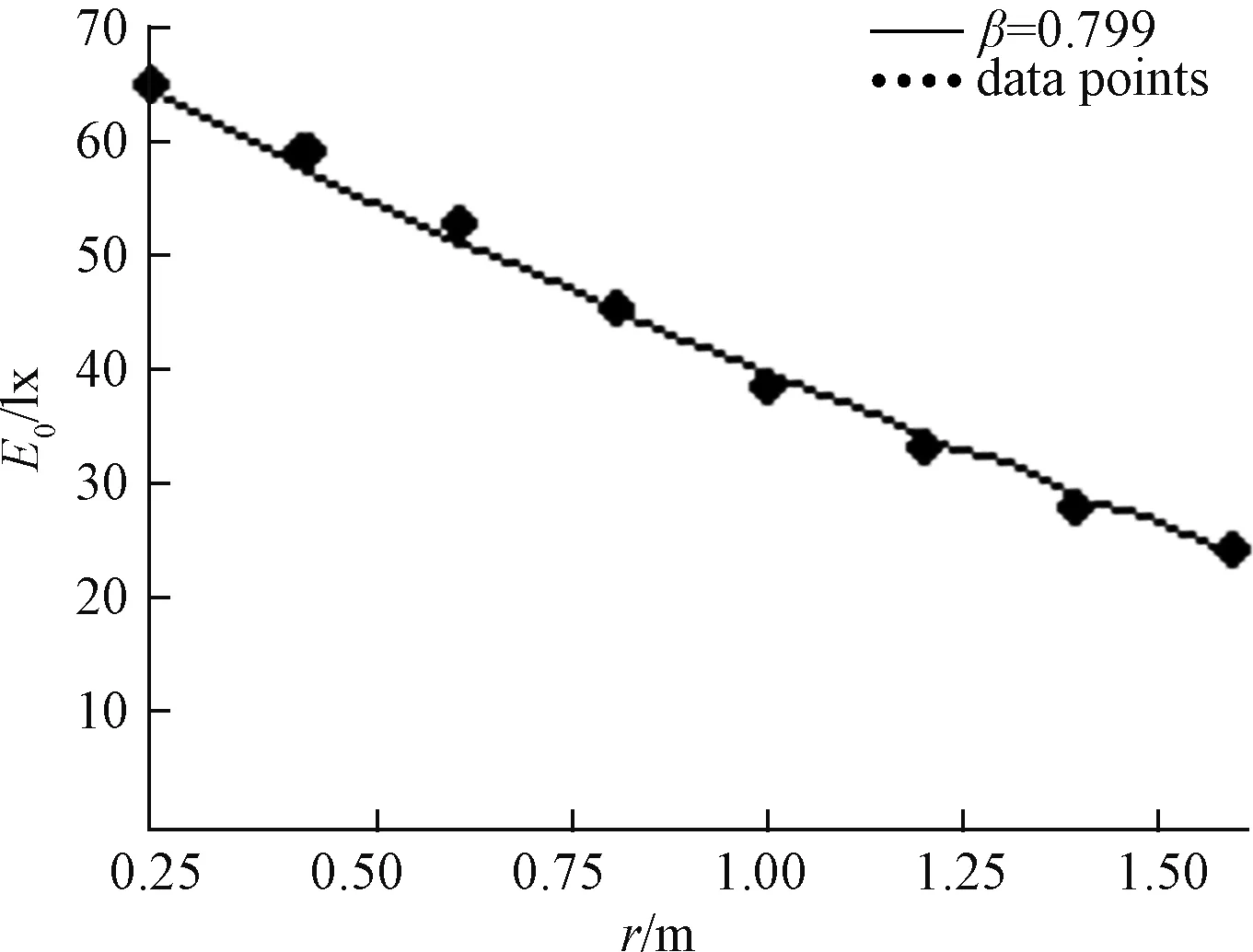
圖8 照度峰值隨陣列半徑的響應曲線Fig.8 Response curves of the peak of intensity illumination versus array radius

3 結論

為了得到LED圓形陣列照度隨自變量的函數變化規律，利用單個LED芯片的照度公式推導出LED圓形陣列光斑的照度峰值公式，即建立了研究LED圓形陣列光斑照度峰值的數值計算方法。在此基礎上利用擬合方法得出了LED圓形陣列光斑的照度峰值隨目標距離、芯片光強以及陣列半徑變化的冪函數公式。這些冪函數公式不僅函數機構簡單，而且能夠很好地與數值計算結果吻合。利用這些冪函數公式能夠十分方便地對LED圓形陣列光斑的照度峰值特性進行解析研究，加深了對LED圓形陣列光斑照度特性內在規律的認識。并且在LED圓形陣列的照明設計中可以利用這些冪函數公式方便地計算出不同照度峰值下對應的目標距離、芯片光強以及陣列半徑，為照明設計提供理論數據。這為了研究LED圓形陣列光斑的照度峰值特性建立了一種新方法，彌補了數值計算方法和仿真軟件不能對LED圓形陣列光斑的照度峰值特性進行解析研究的缺陷。

本文建立的LED圓形陣列照度的冪函數方法與現行的數值計算方法和仿真軟件相比有一下優點：①冪函數方法將LED圓形陣列照度峰值隨目標距離、芯片光強以及陣列半徑的變化規律通過冪函數的形式直觀、清晰、簡潔地表示出來，利用這些公式能夠十分方便地對LED圓形陣列的照度峰值規律進行理論研究，這是現行的數值計算方法和仿真軟件不具備的。②通過冪函數方法還可以得到目標距離、芯片光強以及陣列半徑隨照度峰值變化的函數關系，利用這些關系能夠十分方便地計算出不同照度峰值對應的目標距離、芯片光強以及陣列半徑，為LED圓形陣列的照明設計提供理論數據，這也是現行的數值計算方法和仿真軟件不具備的。

[1] DING Y，LIU X，ZHENG Z R，Freeform LED lens foruniform illumination[J]. Optics Express, 2008, 16(17);12958-12966.

[2] 蘇宙平, 闕立志, 朱焯煒. 用于LED 光源準直的緊湊型光學系統設計[J]. 激光與光電子學進展, 2012, 49(2): 022203.

[3] SUN C C，CHEN C Y，HE H Y. Precise optical modeling for silicate-based white LEDs[J]. Optics Express, 2008, 16: 20060.

[4] SUN C C，CHIEN W T，MORENO I. Analysis of the far-field region of LEDs[J]. Optics Express, 2009, 17(12): 13918-13922.

[5] WANG K, LIU S，CHEN F，LIU Z Y. Freeform LED lens for rectangularly prescribed illumination[J]. Journal of Optics A-Pureand Applied Optics. 2009, 11(10): 105501-105505.

[6] 丁毅，顧培夫. 實現均勻照明的自由曲面反射器[J].光學學報，2007,27(3)：540-544.

[7] 丁毅，鄭臻榮, 顧培夫. 實現LED 照明的自由曲面透鏡設計[J].光子學報，2009,38(6)：1486-1490.

[8] 羅曉霞, 劉華, 盧振武, 等. 實現LED 準直照明的優化設計[J]. 2011，40(9): 1351-1355.

[9] WHANG A J W，CHEN Y Y，TENG Y T. Designing Uniform Illuminance Systems by Surface-Tailored Lens and Configurations of LED Arrays[J]. Journal of Dispersion and Technology, 2009, 5:94-103.

[10] QIN Z，WANG K，CHEN F. Analysis of condition for uniform lighting generated by array of light emitting diodes wit large view angle[J]. Optics Express, 2010, 18: 17460-17476.

[11] SU Zhouping，XUE Donglin，JI Zhicheng. Designing LED array for uniform illumination distribution by simulated annealing algorithm[J]. Optics Express, 2012, 20(S6): 843-855.

[12] 王加文，蘇宙平，袁志軍，等. LED 陣列模組化中的照度均勻性問題[J]. 光子學報,2014,43(6):919-924.

[13] 趙芝璞，季凌燕，沈艷霞，等.基于PSO 粒子群算法的LED 照明系統光照均勻性研究[J].發光學報，2013,34(12)：1677-1681.

[14] 劉沁，劉啟能.圓形LED陣列的照度特性及其應用[J]. 激光雜志,2014,35(6):21-23.

[15] 姚家祎.照明設計手冊(第二版)[M].北京：中國電力出版社，2006：187-188.

Power Function Fitting Methods of the Illumination Peak of LED Circular Array

LIU Qin1， LIU Qineng2

(1.InstituteofDesignandArt,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China;2.CollegeofComputerScienceandInformationEngineering,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)

Using LED illumination formula, the light spot illumination peak formula of LED circular array is deduced. Using fitting method, the power function formula of the illumination peak with target distance and chip light intensity and array radius are obtained, and these formulas can be quite good agreement with the numerical calculation results. Using these formulas can be easily analytical study on the illumination peak characteristics of LED circular array. To study the illumination peak characteristics of LED circular array set up a new method. It makes up for the defects that numerical method can’t analytical study the illumination peak characteristics of LED circular array.

LED; circular array；illumination peak；fitting method；power function

重慶市教委科技項目基金資助項目(KJ130713) 通信作者：劉沁，E-mail：liuqinecho@163.com

O435; O432.2

A

10.3969/j.issn.1004-440X.2017.02.021