整備狀態下的軌道交通車輛車體模態計算分析*

趙士忠 王晉樂 朱 濤

(1.中車青島四方機車車輛股份有限公司,266111,青島;2.西南交通大學牽引動力國家重點實驗室,610031,成都//第一作者,高級工程師)

整備狀態下的軌道交通車輛車體模態計算分析*

趙士忠1王晉樂1朱 濤2

(1.中車青島四方機車車輛股份有限公司,266111,青島;2.西南交通大學牽引動力國家重點實驗室,610031,成都//第一作者,高級工程師)

推導了多自由度剛體振動系統振動頻率和特征向量的解析方法,研究了軌道交通車輛車體設備懸掛方式及其垂向懸掛剛度與車體系統振動頻率和車體各階振幅之間的關系。以某軌道交通車輛車體模態分析為例,對車體模態分析過程中懸掛設備的模擬方法、車體內裝和設備的剛度,以及乘客質量對車體一階垂彎和扭轉頻率的影響進行了深入分析和試驗對比。研究結果表明,設備懸掛方式和懸掛剛度的選擇對車體頻率有非常顯著的影響;與試驗相比,考慮設備懸掛剛度、內裝和設備自身剛度時對車體主要振動模態有顯著提升,應在車體結構設計時予以注意;乘客質量對車體主要振動模態頻率幾乎沒有影響。

軌道交通車輛; 車體模態分析; 振動頻率解析法; 設備懸掛剛度; 內裝剛度; 乘客質量

First-author′s address CRRC Qingdao Sifang Co.,Ltd.,266111,Qingdao,China

研究表明,過低的車體垂向彎曲頻率會降低車體的垂向平穩性[1]。車體一階垂直彎曲和一階扭轉頻率是評價運行安全性和乘坐舒適度的重要參數,也為車體輕量化設計提供參考依據,在車輛前期設計階段對該參數進行計算評估尤為重要。

文獻[2-5]將車體結構視為有限個自由度的離散體,基于有限元法對軌道車輛整備車體進行了模態分析,車體吊掛設備采用質量均布、質量點或修改彈性模量的方法進行模擬,未考慮設備的懸掛方式(剛性或彈性)、設備自身剛度以及乘客的影響。文獻[6]將車體結構等效為自由梁,建立了車體剛柔耦合運動方程,分析了彈性懸掛設備對整備車體模態的影響。文獻[7]基于模態疊加法原理建立了考慮車體彈性振動和車下設備的高速動車組三維剛柔耦合動力學模型,分析了車下設備懸掛方式、重心偏載與彈性懸掛參數對車體振動響應的影響規律。然而,整備車體是由鋼結構、設備、連接件,以及內裝部件等組成,其系統振動不僅包含車體結構自身的剛性和彈性振動,還包含各設備的剛體振動,因此整備車體是一個剛柔耦合振動的系統。車體的各階振動模態由車體結構的剛體振動、彈性振動以及設備的剛體振動疊加而成,所以整備車體的一階垂彎頻率不僅與車體鋼結構一階垂彎固有頻率有關,還與設備的剛體懸掛頻率、內裝和設備剛度有關。另外,乘員質量也是影響車體設計的重要參考指標。因此,在軌道車輛車體結構設計過程中,不僅要考慮鋼結構自身的振動頻率,還應對影響車體模態的各種因素進行綜合評估,以便快速、有效、準確地對設計的車體振動頻率進行評估,使其不僅能滿足整備車體抗振設計的要求,而且可避免結構剛度冗余設計帶來的結構質量不必要的增加。

本文通過推導的多自由度剛體振動系統振動頻率和特征向量解析方法,研究軌道交通車輛車體設備懸掛方式及其垂向懸掛剛度與車體系統振動頻率和車體各階振幅之間的關系,在此基礎上,研究車體模態分析過程中懸掛設備的模擬方法、車體內裝和設備的剛度,以及乘客質量對車體一階垂彎和扭轉頻率的影響,希望從理論和有限元分析手段兩個角度對軌道交通車輛車體模態分析關鍵問題進行全面解析,進而指導車體結構設計。

1 車體懸掛設備振動解析方法

1.1 多自由度剛體振動系統分析

為了研究設備懸掛方式(剛性或彈性)對車體振動頻率尤其是一階垂直彎曲的影響,將軌道交通車輛車體及其主要懸掛件(如主變壓器、牽引變流器)等效為剛體,建立系統多自由度垂向振動力學模型,如圖1所示。圖中,Z0、Z1、Z2、Zi分別為車體、主變壓器、牽引變流器及其它懸掛設備的垂向位移;m0、m1、m2、mi分別為車體、主變壓器、牽引變流器及其它懸掛設備的質量,其中m0為除去橡膠件懸掛質量的車體整備狀態總質量;k0、k1、k2、ki分別為車體、主變壓器、牽引變流器及其它懸掛設備的垂向懸掛剛度。

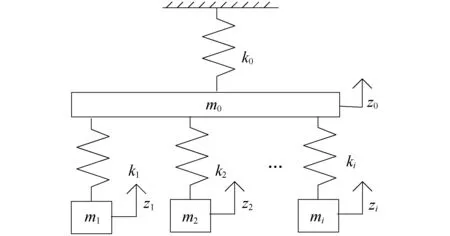
圖1 多自由度車體系統垂向振動模型

k0的表達式為:

k0=(2π·f0)2·m0

(1)

式中:

f0——除去橡膠件懸掛質量的車體整備狀態的一階垂彎頻率。

建立多自由度車體系統的垂向振動方程:

(2)

(3)

將上式轉化為一般表達式形式:

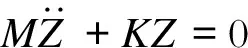
(4)

其中

則

K·Z=λ·M·Z

(5)

求解式(5)的特征根和特征向量,即可求出各部件的振動頻率。

首先,對質量矩陣M進行Cholesky三角分解,即M=L·LT,式(5)變為:

L-1·K·L-T·Z=λ·Z

(6)

對L-1·K·L-T矩陣求解特征值,即可得出部件的振動頻率和特征向量(振型)。

1.2 算例分析

基于某型軌道交通車輛車體相關參數,對以上理論分析進行驗證。車體相關參數如表1所示。

表1 車體及懸掛參數

改變主變壓器的垂向懸掛剛度,得到不同主變壓器垂向懸掛剛度下的系統振動頻率和車體相對振幅,如圖2所示。圖中,相對振幅高的振型為主振型,此時對應的頻率為主振型頻率。

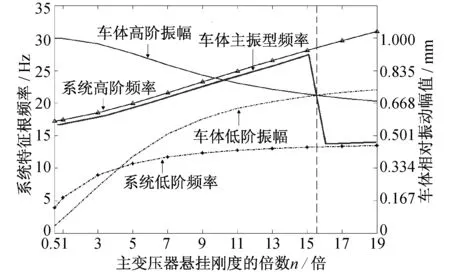
圖2 垂向懸掛剛度與車體系統振動頻率和車體各階振幅的關系

從圖2中可以看出,車體一階垂彎頻率與主變壓器的剛度密切相關,當主變壓器垂向懸掛剛度小于16倍原始剛度時,車體的高階振幅大于低階振幅,主振型(一階垂彎)為高階振動,而當主變壓器垂向懸掛剛度大于16倍原始剛度時,車體的低階振幅大于高階振幅,主振型為低階振動,因此車體對應的主振型頻率是先為系統高階頻率,后為系統低階頻率。這說明設備懸掛方式對車體頻率有非常顯著的影響,在結構設計與仿真分析時必須予以重視。

2 懸掛設備對車體頻率的影響分析

鑒于車體設備懸掛方式對振動模態的影響,以某軌道交通車輛車體模態有限元分析為例,對車體模態分析過程中懸掛設備的模擬方式及其關鍵技術進行詳細解析。車體模態的有限元分析中,設備的模擬通常有以下四種方法:

(1) 將質量單元直接施加于設備安裝位置;

(2) 在設備重心創建一節點,設備質量以集中質量的形式施加在該節點上,然后通過rbe2單元連接在設備安裝座上;

(3) 用規則的立方體模擬設備,并用梁單元將其懸掛在設備安裝座上;

(4) 用規則的立方體模擬設備,并將其懸掛在設備安裝座上,與安裝座的連接以設備實際懸掛方式為準,若為彈性連接,則用具有三向剛度的彈簧單元模擬;若為剛性連接,則用梁單元模擬。

圖3為車體模態分析的有限元模型中主要的吊掛設備分布。圖4為四種模擬方式的模型說明。其中車頂空調、車下變壓器和壓縮機與車體是彈性連接。表2為四種模擬方式的車體模態分析結果。

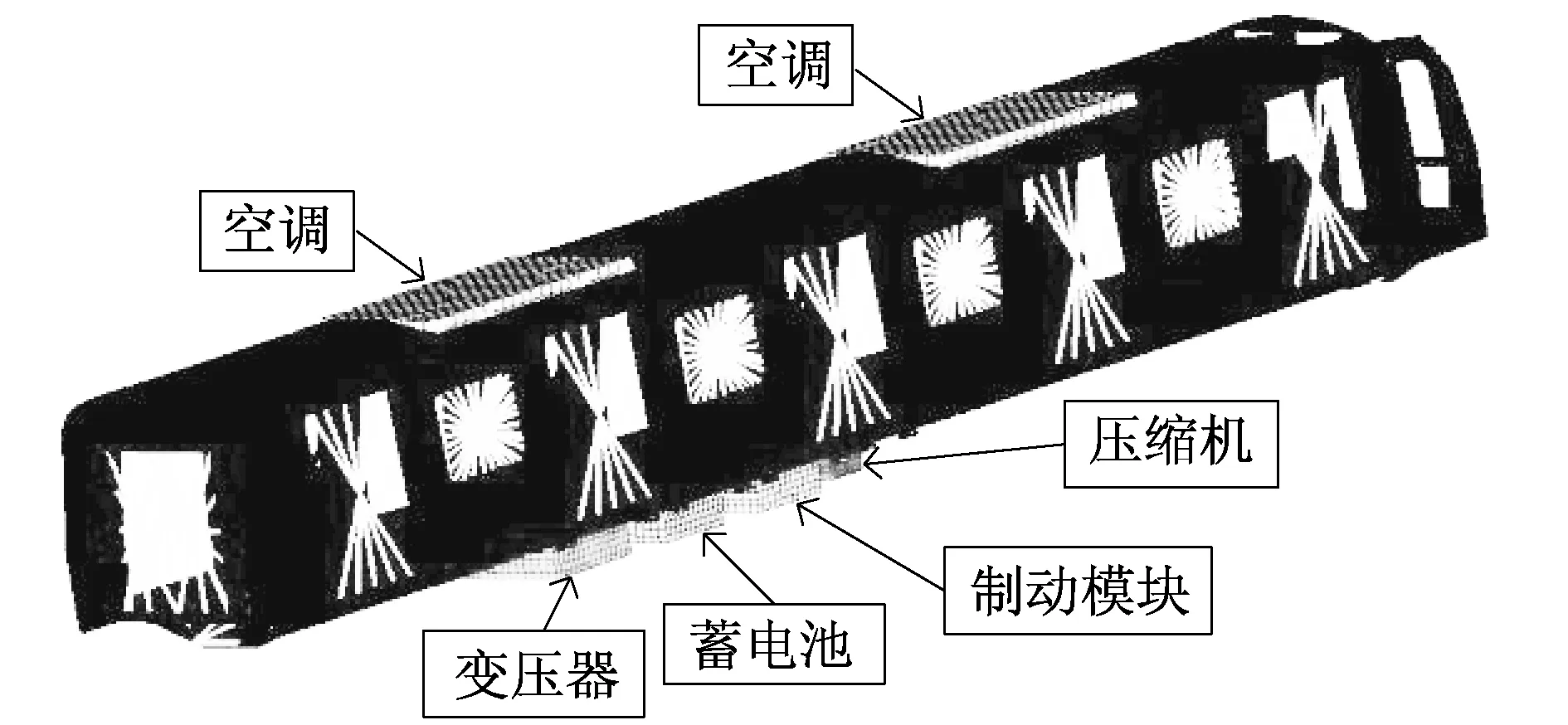
圖3 車體主要吊掛設備

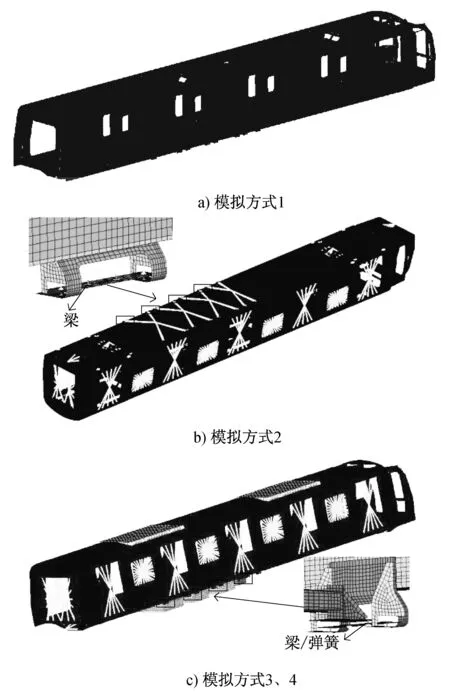
圖4 車體模態分析的有限元模型

從表2可以看出,模擬方式1計算得到的各階頻率均小于試驗值,模擬方式4計算得到的各階頻率與試驗值最接近。這主要是由于,方式1沒有考慮懸掛剛度以及設備本身的剛度對車體頻率的影響,增加了車體垂直彎曲以及扭轉的趨勢;方式4相比于方式2和方式3,既考慮了設備本身的剛度,又考慮了懸掛剛度,因此計算結果誤差最小。

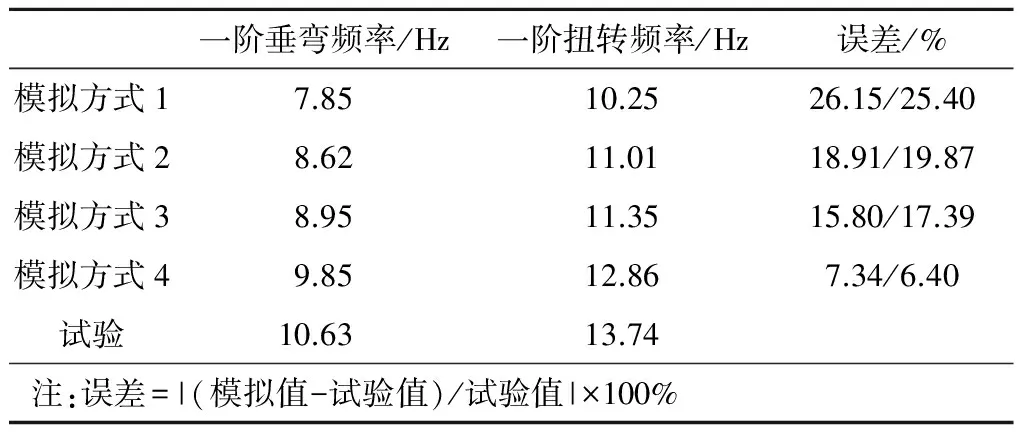
表2 四種模擬方式的車體模態與試驗對比

3 內裝和設備剛度對車體頻率的影響分析

整備車輛在底架下方安裝了變壓器、逆變器、蓄電池箱等設備,在車頂安裝了空調機組,增加了車體的剛性。同時,車體內部裝飾對車體剛度的貢獻也不容忽視。因此,在對整備車輛車體進行模態分析時,設備、內裝的剛度也應予以考慮。

對于吊掛設備,在第2節中提出了用立方體模擬設備的方法,通過與試驗的對比分析,證明了其可行性。但車體上大量無法準確模擬的部件(如車體內裝、木結構、門窗、行李架等)基本均勻地分布在車內,對車體的整體剛度有一定的影響。采用當量彈性模量法對這些部件進行等效替換。對于鋁合金車體,其初始彈性模量(E)為69 GPa,分別將E增加10%和20%,即E為75.9 GPa和82.8 GPa,比較車體主要頻率,結果如表3所示。彈性模量與車體一階垂彎頻率和車體一階扭轉頻率的關系如圖5、6所示。

表3 不同初始彈性模量時的車體主要頻率及其變化率

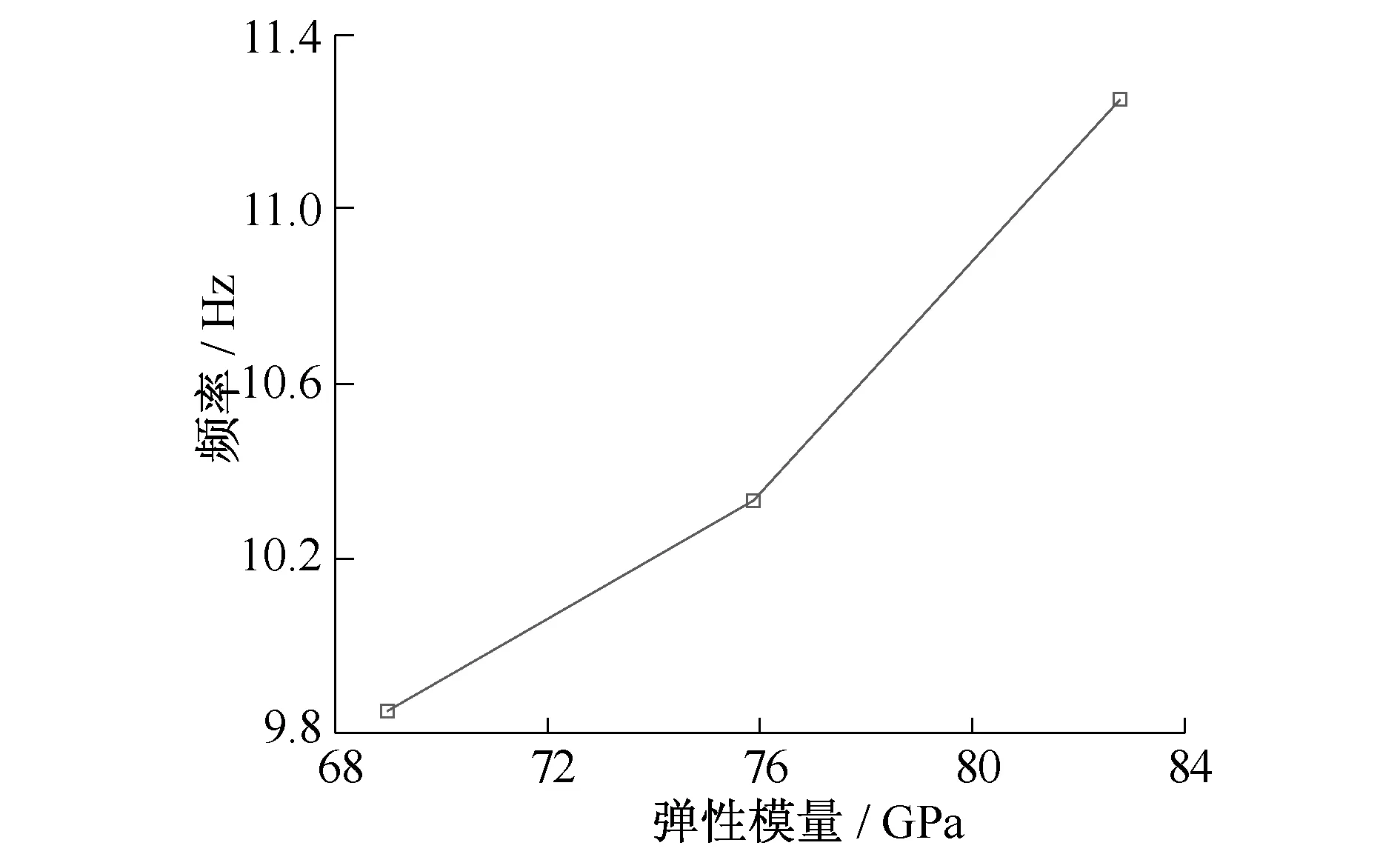
圖5 彈性模量與車體一階垂彎頻率變化關系

圖6 彈性模量與車體一階扭轉頻率變化關系

由表3及圖5、6可以發現,車體固有頻率隨著E的增加而準線性增加。在分析過程中,可根據實車試驗數據或類似車型的試驗數據,利用線性插值的方法修正E值,盡可能地考慮內裝剛度對車體固有頻率的影響,從而更好地指導車體結構設計。

4 乘客質量對車體頻率的影響分析

上、下班高峰期,城市軌道交通車輛內每平米區域高達9人,因此在基于有限元分析的車體結構設計過程中,有必要研究乘客對車體頻率的影響。

為進一步研究車體有限元分析中乘客的模擬方法,保證其在車體模態分析時對一階彎曲固有振動頻率不產生影響,又不影響對車體強度的分析以及舒適性評價,在模擬方式4和考慮彈性模量為75.9 GPa的有限元模型基礎上,增加了乘客的模擬。將乘客看成1個自由度的彈簧進行模型化,乘客的有限元模型如圖7所示。

根據圖7中的有限元模型,計算出車體在AW3 (超載)狀態下(除座椅區域外,每平米站立9人),車體的一階垂直彎曲頻率為10.25Hz(見圖8)。該值與表3中彈性模量75.9GPa的計算值非常接近,說明乘客質量對車體一階垂彎幾乎沒有影響,同時也證明了模擬方式的可靠性。

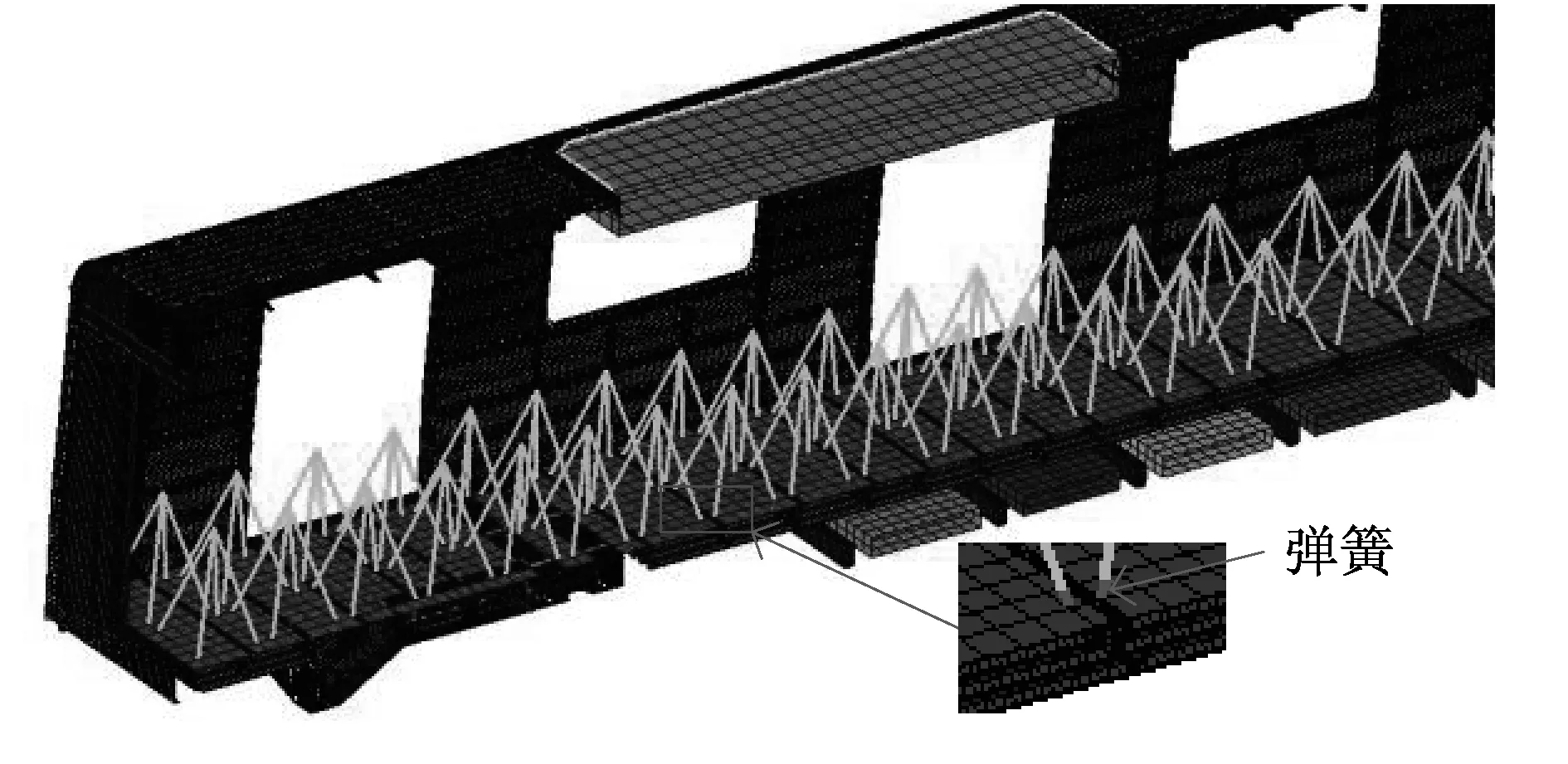
圖7 乘客模擬

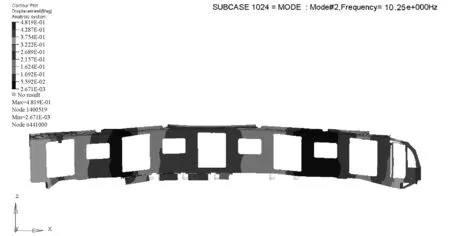
圖8 載有乘客的AW3車體一階垂直彎曲頻率

5 結論

本文研究了軌道交通車輛車體模態分析的若干關鍵問題,得到以下結論:

(1) 設備垂向懸掛剛度的選擇與車體系統振動頻率和振幅密切相關,是車體結構設計不可忽略的重要因素,應在結構模態分析時予以考慮;

(2) 整備車體模態有限元分析時,設備自身剛度以及懸掛剛度的模擬對車體結構模態有重要影響,應在有限元模型模擬其剛度,并對懸掛剛度進行設置;

(3) 車體一階垂彎和扭轉頻率隨車體內裝及設備自身剛度(有限元分析中,通過改變對應結構的彈性模量來實現)的增加呈線性變化關系,在車體結構剛度評估中應該進行適當等效考慮;

(4) 從研究車體振動模態的角度,乘客對車體一階垂彎頻率幾乎沒有影響,將乘客看成彈簧進行模型化更接近客觀實際,有利于乘客對車體輕量化和振動影響的深入分析。

[1] 周勁松,張偉,孫文靜,等.鐵道車輛彈性車體動力吸振器減振分析[J].中國鐵道科學,2009,30(3):86-90.

[2] 羊玢,孫慶鴻,黃文杰,等.地鐵B型車車體靜強度及模態計算[J].交通運輸工程學報,2006,6(2):1-5.

[3] 郝魯波,胡青泥,李剛.整備狀態下客車模態的有限元分析探討[J].鐵道車輛,2004,42(11):4-7.

[4] 魯寨軍.機車車體模態分析中用質量單元模擬設備重量的方法探討[J].電力機車與城軌車輛,2003,26 (1):25-27.

[5] 魯寨軍,田紅旗,周丹.270 km/h高速動車模態分析[J].中國鐵道科學,2005,26 (6):18-23.

[6] 陽光武,肖守訥.彈性懸掛設備對列車整備車體模態的影響分析[J].鐵道機車車輛,2012,32(4):37-40.

[7] 吳會超,鄔平波,曾京,等.車下設備對車體振動的影響[J].交通運輸工程學報,2012,12(5):50-56.

[8] 木村,敏宣.車體振動評估技術的進展[J].國外鐵道車輛,2005,42(3):19-23.

Carbody Modal Analysis for Rail Transit Vehicle under Preparation Conditions

ZHAO Shizhong, WANG Jinle, ZHU Tao

The analytic method of vibration frequency and characteristic vector for multi-degree of freedom rigid body system is deduced,and the relationship between equipment suspension style,vertical suspension stiffness,carbody vibration frequency and vibration amplitude are studied.A railway vehicle carbody modal is taken as an example, the influence of the simulation method of equipment suspension,stiffness of car interior and equipment decoration,as well as the passenger weight to the first order vertical bending and torsion frequencies are analyzed in depth, and compared with test result.This research shows that the selection of equipment suspension style and suspension stiffness has significant effect on carbody frequency.By comparing with the test result,and considering of the equipment suspension stiffness,car interior and equipment decoration stiffness,the main vibration modal stiffness of carbody should have obvious improvement during the carbody structure design, while the passenger weight has little impact on carbody main vibration modal frequency.

rail transit vehicle; cabody modal analysis; vibration frequency analysis method; equipment suspension stiffness; car interior decoration stiffness; passenger weight

*國家科技支撐計劃項目(2015BAG12B01-15);中央高校基本科研業務費專項資金資助(2682015CX046)

U270.2

10.16037/j.1007-869x.2017.04.007

2015-12-29)