UR機器人的運動學和奇異性分析*
□郭小寶 □羅振軍 □趙振
杭州娃哈哈集團機電研究院智能裝備研究所杭州310020
UR機器人的運動學和奇異性分析*
□郭小寶 □羅振軍 □趙振
杭州娃哈哈集團機電研究院智能裝備研究所杭州310020
機器人的正向、逆向運動學是研究機器人運動姿態控制的理論工具,其封閉解問題目前還沒有通用解法,比較常用的是代數方程組數值迭代算法,但難以保證實時性和精度要求。基于矩陣理論分析UR型機器人的機構特點,采用解析方法獲得正向運動學和逆向運動學解法,進而獲取機器人的奇異位置,最后通過MATLAB編程和SolidWorks三維實體模型運動仿真驗證解法的正確性。
1 課題背景
丹麥創新工業機器人制造商Universal Robots公司的UR5及UR10型機器人憑借優異的靈活度、安全性和獨特創新的人機協同功能,在近年來的各屆工業展覽會上受到越來越多的關注。2012年5月,UR5型機器人被國際機器人學聯合會(IFR)及美國電氣和電子工程師協會機器人與自動化學會(IEEE-RAS)評為全球最創新機器人。UR機器人顛覆了笨重且昂貴的傳統工業機器人概念,它憑借創新的技術能夠讓操作者迅速掌握操控技巧,并投放至多個生產流程中[1-2]。
UR機器人是一種六關節機器人,目前國內對其機構運動學的研究較少。機器人的正向、逆向運動學是研究機器人運動姿態控制的理論工具,是指導機器人動作指令的核心部分,簡單且能夠快速執行的運動學算法是機器人實現高速、高精度運行的重要手段[3-4]。
機器人的正向運動學是在已知關節變量的情況下,求解末端執行器的空間位置和姿態;逆向運動學則是在已知末端執行器位置和姿態的情況下,求解關節變量。機器人運動學算法主要有解析法和數值法。解析法包括矢量代數法、幾何法、矩陣法和四元數法等,優點是可以得到全部解,缺點在于難度較大,方法通用性不強。數值解法直接求解約束方程組,可以通過迭代運算求得任何機構的實數解,但通常不能得到全部解,一般而言,初值的選取及搜索算法對收斂性和精度影響較大[5-10]。
基于機器人通用的D-H(Denavit-Hartenberg)矩陣方法,根據機構的結構組成特征建立約束方程組,采用多種方法從約束方程組中消去中間參數,獲得單參數多項式后再求解,并詳細推導正向運動學和逆向運動學解法及機器人奇異位置,推導過程簡單、直觀。最后通過工程實例,采用MATLAB編程和SolidWorks三維實體模型運動仿真驗證運動學解法的準確性。
2 UR機器人運動學模型
UR機器人三維模型如圖1所示,這是一種六自由度機器人,包括底座、腰部、大臂、小臂、手腕頭、手腕尾、末端法蘭7個基本部件,相鄰兩個部件之間通過轉動關節連接。
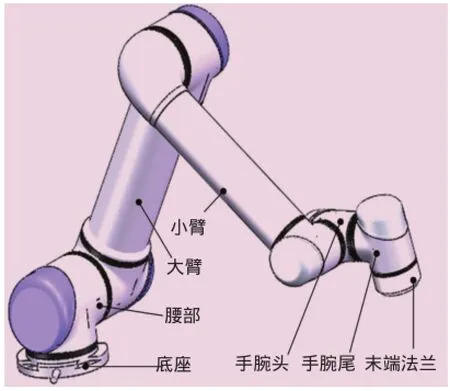
圖1 UR機器人三維模型
相比傳統的六自由度機器人,UR機器人具有各個關節都能整周回轉的優點,且由于UR機器人機構特點滿足機器人機構學的Pieper準則[11],因此其運動學逆解具有封閉解的優勢,使運動控制更為容易。
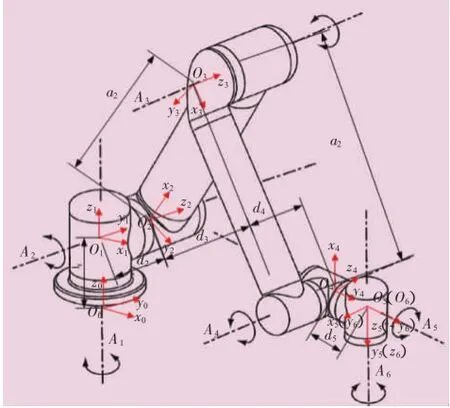
圖2 UR機器人機構簡圖
UR機器人6個轉動關節軸線Ai中,A1和A2相互垂直,A2、A3、A4相互平行,A4和A5相互垂直,A5和A6相互垂直。采用D-H矩陣分析法建立各個關節連桿坐標系,機器人桿長參數見表1。
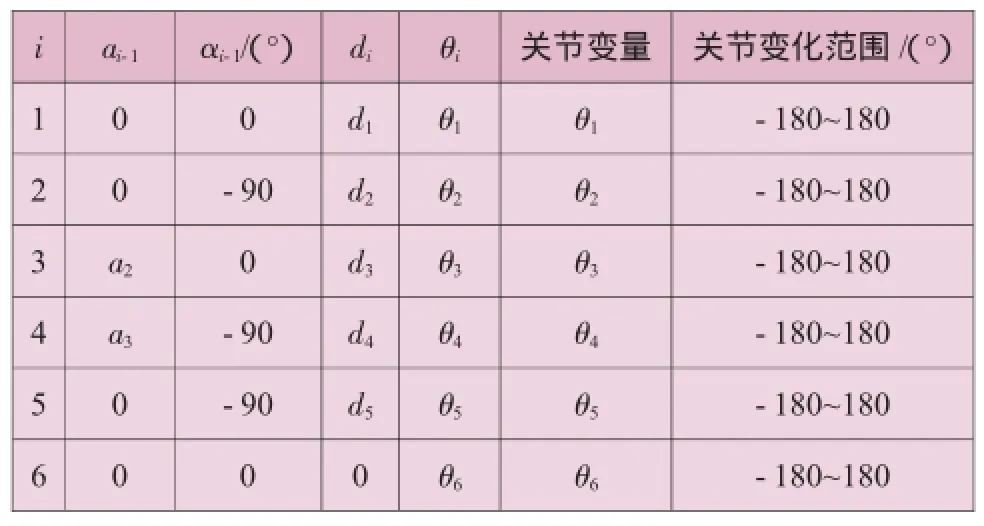
表1 機器人桿長參數和關節變量
3 UR機器人運動學算法研究
機器人運動學主要解決機器人驅動關節變量與末端剛體位姿坐標(操作空間變量)之間的映射關系,可以為機器人的運動控制提供理論基礎,是實現機器人閉環實時精確控制的重要一環。
3.1 正向運動學
為了簡化三角函數符號,下文中用ci表示cosθi的值,用si表示sinθi的值,用c234表示的值,用s234表示sin(θ2+θ4+θ4)的值。
連桿之間變換矩陣可以表示為:

由此,可以求出連桿變換積:

從而正向運動學可以表示為:
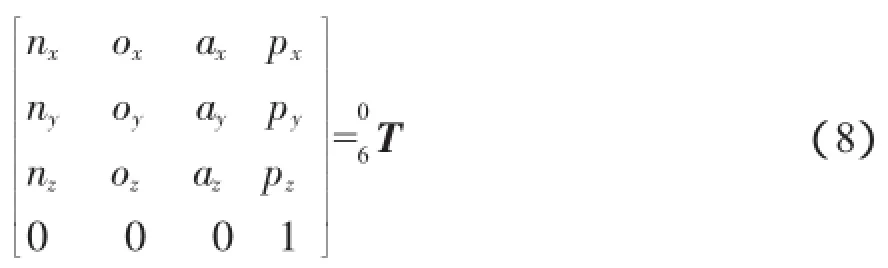
3.2 逆向運動學

對比式(9)和式(10),矩陣的第2行第4列元素為常數,即可獲得求解θ1的一元方程:

通過三角函數萬能公式,可求出θ1:
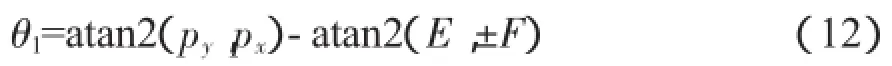
然后可求解θ5和θ6,對比式(9)和式(10),由矩陣的第2行前三列元素可以獲得關于θ5和θ6的方程:

聯立式(13)和式(14),消除變量,得:
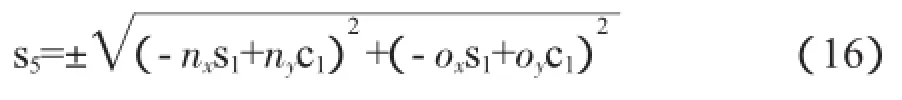
聯立式(15)和式(16),即可求出θ5:

觀察式(13)和式(14),可得:當s5=0,即θ5=0或θ5=π時,機構發生奇異,無法求出θ6;當s5≠0,即θ5≠0且θ5≠π時,可以求出θ6:
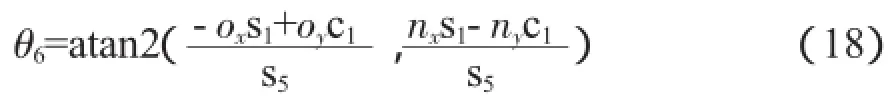
對比式(9)和式(10),由矩陣第1行第3列和第3行第3列兩列元素可以導出如下方程:

當s5=0,即θ5=0或θ5=π時,機構發生奇異,無法求出θ2+θ3+θ4;當s5≠0,即θ5≠0且θ5≠π時,此時可以求出θ2+θ3+θ4:
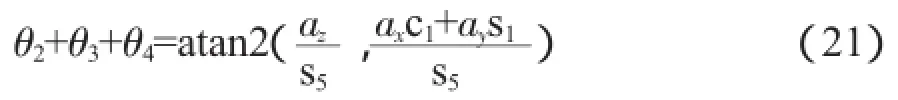
對比式(9)和式(10),由矩陣第1行第4列和第3行第4列兩列元素可以導出如下方程:
2.4 血糖(Glu)和皮質醇(Cor) 兩組病人組間比較,T3、T4時間點B組Glu和Cor均高于A組,且差異有統計學差異(P<0.01)。A組Glu于T4時明顯高于T1(P<0.05);A 組 Cor于 T3、T4時較 T1顯著升高(P<0.01)。 B 組 Glu 于 T2~T4時明顯高于 T1(P<0.01);B組 Cor于 T3、T4時明顯高于 T1(P<0.01)。 見表 4。
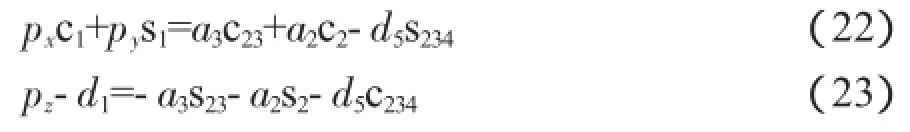
聯立式(22)和式(23),消除變量θ2+θ3,可以獲得求解θ2的一元方程:

從而可以求解出θ2:
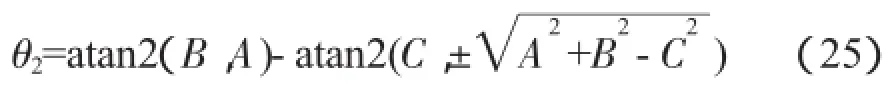
在求解θ2后,再次聯立式(22)和式(23),即可求出θ2+θ3:
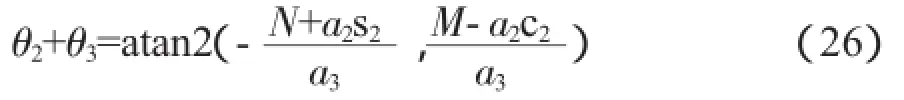
從而可以求出θ3與θ4。
至此,逆向運動學的結果,即6個關節變量均已求出。
4 UR機器人奇異性分析
機器人在奇異點位置時,逆向運動學求解表達式無解,無法通過逆向運動學運算將末端笛卡爾坐標系轉化為關節電機軸的角度,而且笛卡兒坐標系內一點微小的變化就會引起軸角度的劇烈變化,所以需要獲得奇異點位置的直觀表達,避免機器人失控。
(2)肘部奇異位置表達式。當A2+B2-C2=0時,無法求出θ2,導致機構失控,軸線z2、z3、z4共面。
(3)腕部奇異位置表達式。當s5=0,即θ5=0或θ5=π時,軸線z4和z6平行,無法求出θ6,導致機構失控。
5 工程實例驗證
5.1 MATLAB驗證
在MATLAB開發環境下,根據前述運動學算法編寫如圖3所示的正向、逆向運動學算法腳本,腳本代碼不足30行,完全為順序結構,沒有任何數值迭代,具有較快的執行速度。
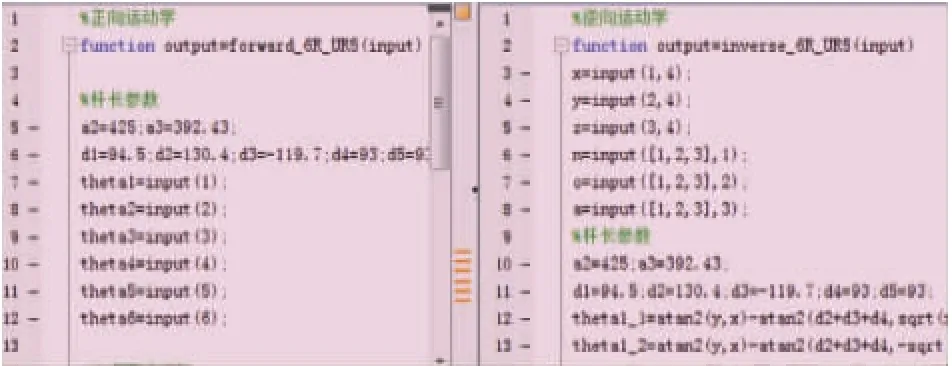
圖3 運動學算法MATLAB腳本截圖
運動學測試點如下。
通過MATLAB校驗,運動學測試點滿足正向運動學和逆向運動學算法,從而驗證了解法的有效性和正確性。
5.2 運動仿真驗證
為了反映運動學算法的真實性,在SolidWorks三維建模軟件下設計UR機器人模型,定義配合和約束條件。
驗證時,規劃機器人工作空間末端法蘭的運動軌跡,在y-z平面上的軌跡如圖4所示。
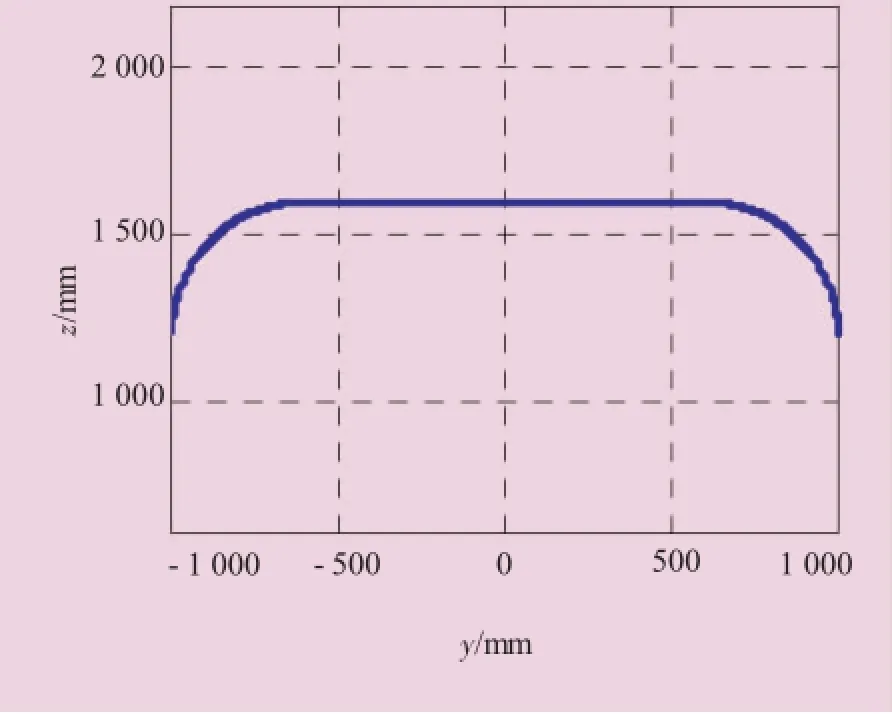
圖4 機器人末端控制點在y-z平面內軌跡
通過逆向運動學和軌跡規劃,計算出各驅動軸的關節角位移,如圖5所示。
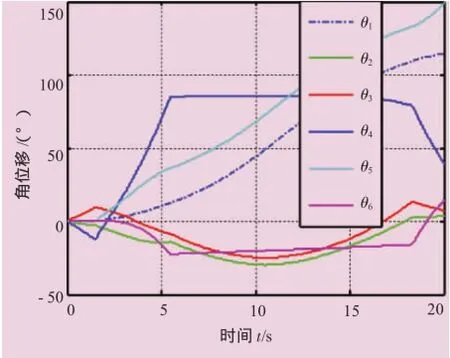
圖5 各驅動軸關節角位移曲線
將各關節的角位移導入基于SolidWorks設計的UR機器人模型,作為各關節驅動伺服電機的輸入量,經過實時運動仿真獲得如圖6所示的模擬軌跡,該模擬軌跡與預先規劃的軌跡完全一致,從而驗證了運動學解法的正確性。
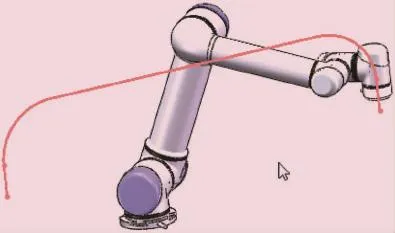
圖6 UR機器人運動仿真末端模擬軌跡
6 結論
基于D-H矩陣法研究了UR機器人運動學的解析算法,得出了結論。
(1)分析了UR機器人的機構類型,得出了其具備運動學封閉解的條件。
(2)通過D-H矩陣法,根據UR機器人機構的結構組成特征建立約束方程組,獲得了簡單直觀的運動學算法。
(3)通過分析得出了UR機器人三種類型奇異的數學表達式,為機器人機構奇異處理和運動控制提供了重要參考。
(4)以MATLAB和SolidWorks軟件為工具,通過三維運動仿真驗證了UR機器人運動學解法的正確性和有效性。
[1]博達.Universal Robots(優傲機器人)推出UR3新型機器人——全球最靈活輕便[J].機械制造,2015,53(4):13.
[2]石強.UR:讓“力控制”感知你[J].今日工程機械,2013(10):68-69.
[3]錢暉.多傳感器融合技術在智能機器人系統中的應用[J].上海電氣技術,2010,3(2):44-48.
[4]王昊杰,薛強.一種三坐標并聯動力頭——Sprint Z3的運動學逆解及尺度綜合[J].機床與液壓,2011,39(17):53-56.
[5]郭小寶,趙振,陳落根.碼垛機器人運動學幾何解法的研究[J].裝備機械,2015(4):44-47.
[6]黃真,趙永生,趙鐵石.高等空間機構學[M].北京:高等教育出版社,2006.
[7]陸晶,高國琴,朱彩紅,等.新型三平移并聯機構的運動分析和工作空間分析[J].機械設計與制造,2007(11):163-165.
[8]LI Y M,XU Q S.Kinematic Analysis of a 3-PRS Parallel Manipulator[J].Robotics and Computer-Integrated Manufacturing,2007,23(4):395-408.
[9]劉辛軍,汪勁松,李劍鋒,等.一種新型空間3自由度并聯機構的正反解及工作空間分析[J].機械工程學報,2001,37(10):36-39.
[10]蔡自興.機器人學[M].北京:清華大學出版社,2000.
[11]熊有倫.機器人技術基礎[M].武漢:華中理工大學出版社,1996.
(編輯:啟德)
The forward and reverse kinematics of robots are the theoretical tools for researching the control of robot motion attitude.There is no general solution for its closed solution.Numerical iterative algorithms with algebraic equations is used more commonly,but it is difficult to guarantee real-time and accuracy requirements. Based on matrix theory,analyzed the mechanical feature of UR robot and obtained the solution for forward kinematics and inverse kinematics by using analytic method,and thus the singular position of the robot could be obtained.Finally,the correctness of the solution was verified by motion simulation established by MATLAB programand 3D solid model in SolidWorks.
機器人;運動學;奇異性;矩陣
Robot;Kinematics;Singularity;Matrix
TH242.2
A
1672-0555(2017)01-001-05
*國家科技重大專項(編號:2011ZX04013-011)
2016年8月
郭小寶(1988—),男,碩士,助理工程師,主要從事機器人結構設計和運動控制研究工作

