偏心梁和非偏心梁建模方法合理性分析
王健明,盧慧敏,戴睿,張少雄
(1.上海船舶研究設計院,上海 201203;2.中國船級社 江蘇分社,南京 210000;3.武漢理工大學 交通學院,武漢 430063)
偏心梁和非偏心梁建模方法合理性分析
王健明1,盧慧敏1,戴睿2,張少雄3
(1.上海船舶研究設計院,上海 201203;2.中國船級社 江蘇分社,南京 210000;3.武漢理工大學 交通學院,武漢 430063)
為了驗證《結構共同規范》、《雙殼油船規范》規定的非偏心梁和CSR散貨船規范規定的偏心梁屬性定義的合理性,采用一加筋板模型,利用MSC.Patran/Nastran對比在復雜彎曲狀態下板梁組合模型有限元收斂解與同量級全板元位移及應力結果,發現偏心梁模型結果與全板元相對誤差能夠滿足工程需求,非偏心梁不能滿足工程需求。對比一條散貨船和一條雙殼油船發現,偏心梁與非偏心梁應力差距最大可達100.70 MPa,與普通鋼的屈服極限235比值為42.85%。偏心梁模型計算結果更加符合實際,驗證了CSR-H摒棄非偏心梁的合理性。
CSR;偏心梁;非偏心梁;復雜彎曲
CSR(common structural rules)《散貨船共同規范》和CSR《雙殼油船共同規范》是2本獨立的規范,對其中不協調部分進行協調是必然趨勢。2009年,GBS在IMO的大力推動下,于MSC 87次會議確定了GBS符合性驗證導則,確定了對IACS《共同結構規范》進行GBS符合性驗證。在IACS理事會C60會議上,對協調后的《共同結構規范》(CSR-H)的性質和涵蓋范圍進行了明確。首先,CSR-H是協調一致、合二為一的一本規范;第二,HPT工作組協調后的規范內容必須符合GBS的要求,列入項目目標范圍。這樣,CSR-H的重要性上升到了新的高度,未來CSR-H規范一方面應該是完成協調要求的規范,同時也是滿足GBS要求的規范[1]。
為了適應GBS的要求,CSR-H更講究規范背后的技術論證,相關的技術背景文件和資料必須要滿足IMO GBS審核的要求[1]。2012年7月,IACS向工業界發布了CSR-H(EXTERNAL RELEASE 1 JUL 2012)。CSR和CSR-H對于有限元直接計算(direct strength analysis,DSA)中,梁單元建模方法存在差異。在有限元結構設計分析中,對梁的受力形式以及在空間放置方式等的理解直接影響整個分析計算結果[2]。
CSR《散貨船規范》規定梁截面屬性采用偏心梁,以板中面處的節點M作為主節點,梁的形心處節點S作為從節點,認為主從節點間用剛臂連接。梁的抗彎慣性矩按梁的形心軸計算[3]。然而,CSR《雙殼油船規范》規定,梁截面形式采用非偏心梁,把節點取在板的中面處,梁的形心取在板的中面上。梁的抗彎慣性矩考慮梁本身截面和帶板(兩邊均為縱骨間距的一半)來計算[4]。具體截面形式見圖1和圖2。
2012年7月發布的CSR-H協調《共同結構規范》擯棄了CSR《雙殼油船共同規范》規定的非偏心梁截面屬性,取的是偏心梁截面屬性[5]。為對比分析這兩種截面形式的可靠性,采用一加筋板將偏心梁和非偏心梁收斂解與全板元結果進行對比,并以兩種截面屬性,分別計算一條散貨船和一條油船,得出主要縱向構件應力差值,以驗證CSR-H梁單元屬性的合理性。
1 板架分析論證
1.1 計算對象
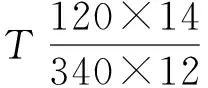
計算坐標系以船底板左端面中點為原點,x軸向前為正方向,y軸向左舷為正方向,z軸向上為正方向,見圖3。
1.2 技術路線
建立上述加筋板模型,采用以下2種邊界條件和載荷進行計算分析。
1)模型1。邊界條件為四周剛性固定,底板承受均布水壓力4 MPa;采用以下分級網格模型,800 mm×800 mm、400 mm×400 mm、200 mm×200 mm、100 mm×100 mm、50 mm×50 mm、25 mm×25 mm和12.5 mm×12.5 mm進行計算。
取A點(1 200,0,0)和B點(1 200,800,0)的位移、XComponent和von Mises值與板厚量級模型(12.5 mm×12.5 mm)進行比較,分析得到收斂解的網格大小[6]。
2)模型2。邊界條件為自由支持,前后兩端承受拉力,并承受面內均布水壓力,以模型1得到的有限元收斂解的網格大小(經驗算為50 mm×50 mm的網格)為基準建立全板元、偏心梁和非偏心梁3種模型,分析比較哪種梁截面和全板元最貼合。
1.3 收斂性證明
從表1可知:偏心梁模型的位移和von Mises值在網格大小為50 mm×50 mm時已經收斂,相對板厚量級網格誤差最大為0.3%,故可以認為50 mm×50 mm網格計算結果為板梁組合模型的收斂解。而非偏心梁在模型1的邊界條件和載荷作用下,中面應力恒為0,這與實際情況相悖。
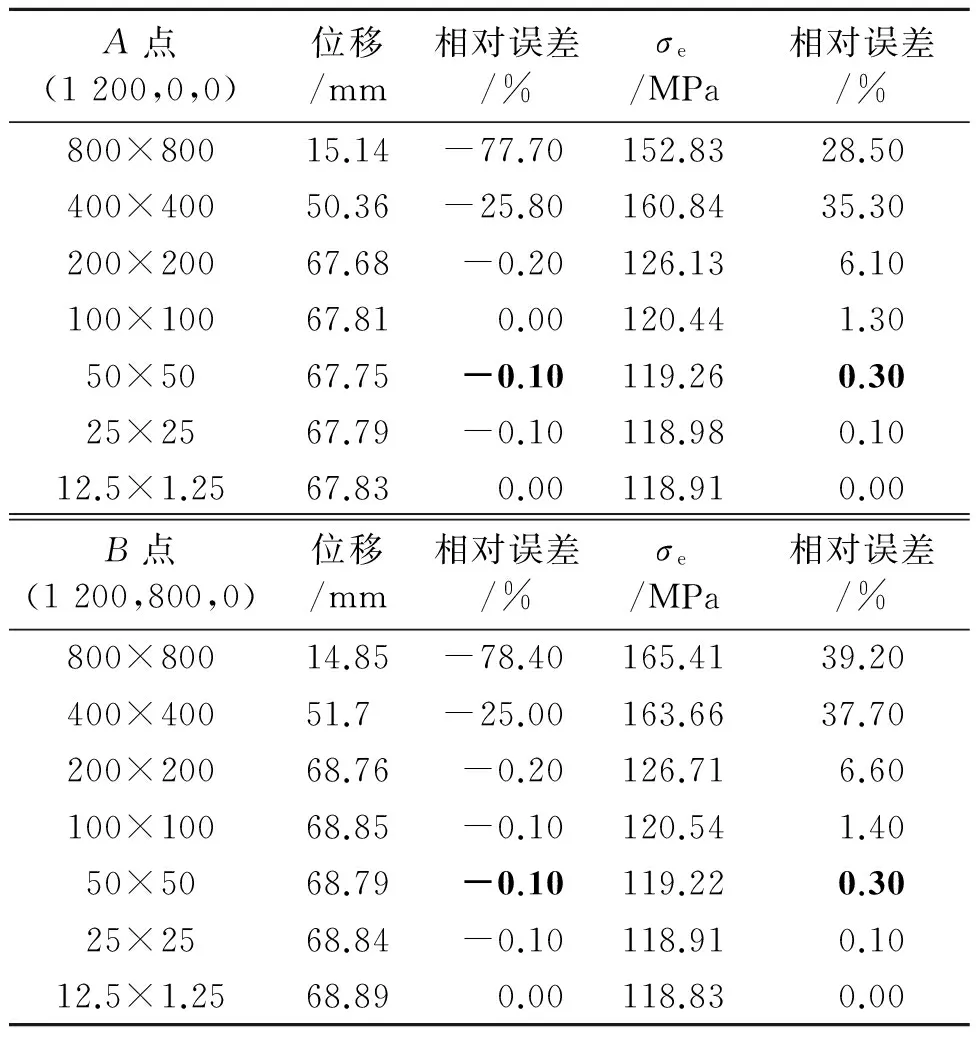
表1 隨著網格逐級細化,A、B點位移和von Mises值 及板厚量級網格的誤差
以下分析可采用50 mm×50 mm全板元應力結果作為基準,對比偏心梁和非偏心梁2種計算模型的應力和應變值,判斷出哪種梁截面形式更加準確。
1.4 復雜彎曲時,偏心梁和非偏心梁位移及應力結果與全板元的對比
利用偏心梁和非偏心梁分別建立加筋板的計算模型,模型均以50 mm為基準建立網格,邊長比盡量接近1∶1。將縱骨用板單元模擬,仍然以50 mm為基準劃分網格,建立全板元模型。采用如下邊界條件和載荷進行:四周自由支持,左右兩側節點承受150 kN的水平拉力,方向相反;底板承受均布水壓力0.2 MPa。
四周邊界約束z向位移,對稱軸ab約束y位移和繞x、z軸向轉角,對稱軸cd約束x位移和繞y、z軸向轉角。
由于梁改板及節點力分配不協調的問題,為了保持板梁組合模型與全板元載荷的一致性,縱骨與底板交點不加節點力,在兩側節點施加水平拉力是為了模擬實際底板是復雜彎曲狀態。
1.5 應力對比單元
取圖4和圖5所示單元為位移和應力對比位置,其中Stiff-for、Stiff-mid和Stiff-end 3個單元形心為船底板縱骨中和軸位置。
1.6 全板元結果
表2、表3為全板元對比單元的位移及應力值,圖6、圖7為應力云圖。
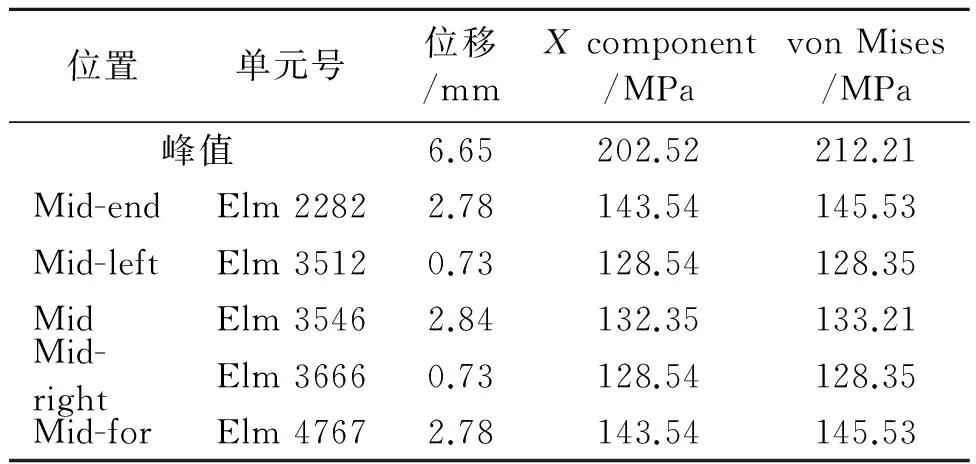
表2 外底板對應單元的位移、X Component和 von Mises值(全板元模型)

表3 縱骨對應單元的X Component值(全板元模型)
1.7 對比分析
偏心梁和非偏心梁與全板元相對誤差見表4和表5。
1)從圖4選定的底板的5個單元對比可知,偏心梁模型板單元形心處位移相對全板元最大誤差為-6.84%,非偏心梁最大是240.77%;Xcomponent相對全板元誤差最大為-0.54%,非偏心梁最大是-9.03%;von Mises相對全板元誤差最大為-0.55%,非偏心梁最大是-9.84%。
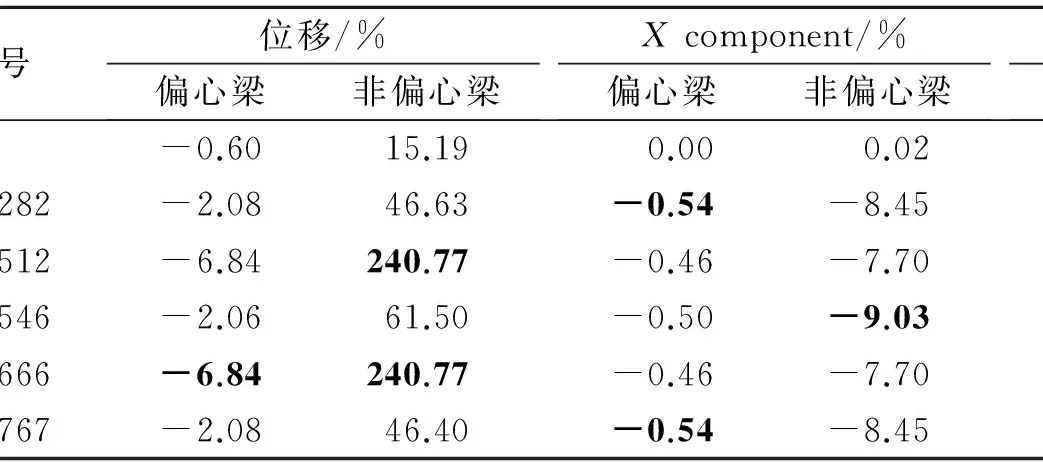
表4 偏心梁和非偏心梁單元形心處位移、X component和von Mises與全板元相對誤差
2)底板對比可知,偏心梁模型板單元形心位移峰值相對全板元最大誤差為-0.60%,非偏心梁最大是15.19%;Xcomponent峰值相對全板元誤差最大為0.00%,非偏心梁最大是0.02%;von Mises峰值相對全板元誤差最大為3.72%,非偏心梁最大是21.25%。
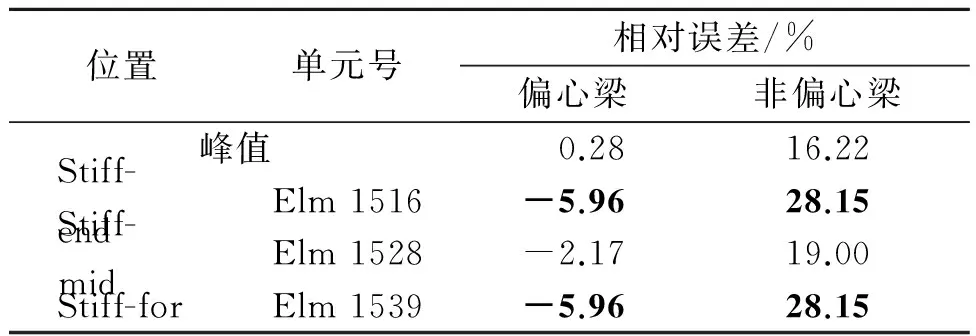
表5 偏心梁和非偏心梁梁單元軸心處X component 與全板元相對誤差
3)從圖5選定的3個單元對比梁單元軸向應力Xcomponent可知,偏心梁模型梁單元軸心處相對板單元對應位置的誤差最大為-5.96%,非偏心梁最大為28.15%。
2 實船艙段對比分析
分別采用某型散貨船和油船進行實船驗證,計算思路見圖8。
主要縱向構件應力差值云圖如圖9和圖10。
由圖9和圖10可知,CSR規定的偏心梁和非偏心梁截面屬性對于計算結果影響較大,其中散貨船最大差值為37.5 MPa,油船最大差值為100.7 MPa,與普通鋼屈服極限比值為42.85%。
3 結論
1)非偏心梁模型對于承受面內壓力和軸向拉伸的復雜彎曲下,加筋板的位移及應力結果相對同量級全板元誤差超過工程允許范圍。
2)偏心梁模型板單元應力及梁單元軸心處應力與全板元模型應力基本吻合,能夠滿足工程計算的要求。
3)驗證了CSR-H摒棄非偏心梁,采用偏心梁截面屬性的合理性。
[1] XU Hua. Invisible opportunity of CSR-H[J]. China ship survey,2011(2):33-34.
[2] 孫秀峰,谷良賢,姜晉慶.MSC.NASTRAN中偏心梁的有限元建模問題[J].彈箭及制導學報,2005,25(1):249-250.
[3] IACS.Common structural rules for bulk carrier[S].2012.
[4] IACS.Common structural rules for double hull oil tank[S].2012.
[5] IACS.Common structural rules for bulk carriers and oil tankers[S],1 JUL 2015.
[6] 楊剛.一種MSC.NASTRAN中偏心梁有限元計算結果修正方法[J],科學技術與工程,2011,11(33),83-86.
[7] 張少雄,陳南華,張偉.8 000 t級江海直達駁船的全船結構強度直接計算[J].船海工程,2005(5):39-41.
[8] 楊永謙.有限元法及其在結構分析中的應用[M].大連:大連海運出版社,1992.
Modeling Method Rationality Analysis of Eccentric Beam and In-Plane beam
WANG Jian-ming1, LU Hui-min1, Dai Rui2, ZHANG Shao-xiong3
(1.Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China;2.Jiangsu Branch of China Classification Society, Nanjing 210000, China;3.School of Transportation, Wuhan University of Technology, Wuhan 430063, China)
In order to validate the rationality of the in-plane beam in common structural rules (CSR) for double hull oil tankers and the eccentric beam in CSR for bulk carriers, a stiffened plate model was established in MSC Patran/Nastran. In the complex bending state, the convergence of displacement and stress in beam-plates combination model and the data in full plate element with the same mesh size was contrasted. It was found that the differences between the eccentric beam model and the full plate element are small, which can meet the engineering requirements, while the in-plane beam model can't meet the engineering requirements. Through a comparative analysis of a bulk carrier and a double hull tanker, the largest gap of the in-plane beam and full plate model can reach 100.70 MPa. So the eccentric beam modeling method is more reasonable.
CSR; eccentric beam; in-plane beam; complex bending
10.3963/j.issn.1671-7953.2017.02.010
2016-08-25
王健明(1989—),男,碩士,助理工程師
U661.43
A
1671-7953(2017)02-0044-05
修回日期:2016-09-20
研究方向:船舶結構設計

