基于動(dòng)態(tài)控制模型的產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移合作博弈研究

吳 潔, 彭星星,盛永祥,李 鵬,施琴芬

(1.江蘇科技大學(xué)經(jīng)濟(jì)管理學(xué)院,江蘇 鎮(zhèn)江 212003；2.南京郵電大學(xué)科技處,江蘇 南京 210003)

?

基于動(dòng)態(tài)控制模型的產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移合作博弈研究

吳 潔1, 彭星星1,盛永祥1,李 鵬1,施琴芬2

(1.江蘇科技大學(xué)經(jīng)濟(jì)管理學(xué)院,江蘇 鎮(zhèn)江 212003；2.南京郵電大學(xué)科技處,江蘇 南京 210003)

運(yùn)用博弈論研究產(chǎn)學(xué)研合作中的知識(shí)轉(zhuǎn)移問(wèn)題，構(gòu)建產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移動(dòng)態(tài)控制模型，計(jì)算高校和企業(yè)在合作博弈狀態(tài)下獲取最大收益時(shí)的納什均衡投入和最優(yōu)獲利能力，分析資源限制水平、共生作用系數(shù)變動(dòng)下納什均衡投入和最優(yōu)獲利能力的變化情況。模擬分析表明，高校和企業(yè)可以根據(jù)系統(tǒng)內(nèi)的知識(shí)產(chǎn)出量和吸收量來(lái)調(diào)整對(duì)知識(shí)產(chǎn)出和知識(shí)吸收的控制投入，從而影響產(chǎn)學(xué)研的最優(yōu)獲利能力；提高共生作用系數(shù)或降低資源限制水平均可降低產(chǎn)學(xué)研的納什均衡投入，提高其最優(yōu)獲利能力。

知識(shí)轉(zhuǎn)移;產(chǎn)學(xué)研合作;動(dòng)態(tài)控制模型;合作博弈

1 引言

加快建立以企業(yè)為主體、市場(chǎng)為導(dǎo)向、產(chǎn)學(xué)研相結(jié)合的技術(shù)創(chuàng)新體系是提高國(guó)家自主創(chuàng)新能力的重要途徑[1]。高校與企業(yè)之間的合作創(chuàng)新能夠使雙方獲得資金上的增加，并且可以作為經(jīng)濟(jì)增長(zhǎng)的引擎[2]。產(chǎn)學(xué)研合作創(chuàng)新實(shí)質(zhì)上是合作各方知識(shí)轉(zhuǎn)移的過(guò)程[3]，以促進(jìn)知識(shí)增值從而實(shí)現(xiàn)知識(shí)向現(xiàn)實(shí)生產(chǎn)力的轉(zhuǎn)化。知識(shí)轉(zhuǎn)移的增值成為產(chǎn)學(xué)研合作成功的關(guān)鍵[4]。

知識(shí)轉(zhuǎn)移的雙方都希望從知識(shí)轉(zhuǎn)移中得到戰(zhàn)略收益以及經(jīng)濟(jì)收益[5]，為了獲得更大收益，轉(zhuǎn)移雙方會(huì)傾向于做出對(duì)自身更有利的行為。因此，知識(shí)轉(zhuǎn)移的過(guò)程也是轉(zhuǎn)移雙方在內(nèi)容、方式等方面博弈的過(guò)程[6]。現(xiàn)有的研究從多個(gè)角度分析了知識(shí)轉(zhuǎn)移的博弈情況，如Lin Lihui等[7]借助博弈論中的信號(hào)博弈模型來(lái)描述知識(shí)轉(zhuǎn)移過(guò)程；李洋[8]等構(gòu)建激勵(lì)下的演化博弈模型，研究博弈主體知識(shí)轉(zhuǎn)移過(guò)程中的努力投入演化情況；Jiang Zhangsheng[9]等構(gòu)建了技術(shù)創(chuàng)新聯(lián)盟內(nèi)知識(shí)轉(zhuǎn)移博弈的兩階段模型，分析了不同所有權(quán)和學(xué)習(xí)能力情況下聯(lián)盟的穩(wěn)定性;Li和Li[10]運(yùn)用博弈方法分析實(shí)踐社群知識(shí)共享的激勵(lì)機(jī)制，發(fā)現(xiàn)若高知識(shí)共享效率實(shí)踐社群比低知識(shí)共享效率實(shí)踐社群的共享成本低，則完全信息條件和不完全信息條件下的實(shí)踐社群知識(shí)共享效益相同。Bandyopadhyay[11]等建立的外包項(xiàng)目中知識(shí)共享的博弈模型，分析了不同知識(shí)水平下知識(shí)共享雙方的最高收益。Szulanski[12]等考慮到知識(shí)轉(zhuǎn)移的時(shí)間選擇，在前期轉(zhuǎn)移和后期轉(zhuǎn)移兩種模式下分析最優(yōu)知識(shí)轉(zhuǎn)移方法，提出知識(shí)轉(zhuǎn)移難度由轉(zhuǎn)移知識(shí)的因果模糊性及知識(shí)轉(zhuǎn)移雙方關(guān)系決定。國(guó)內(nèi)研究最多的是知識(shí)轉(zhuǎn)移的策略，即轉(zhuǎn)移主體根據(jù)對(duì)合作對(duì)方行為的判斷決定是“轉(zhuǎn)移”還是“不轉(zhuǎn)移”，如許學(xué)國(guó)等[13]根據(jù)生物回升模型模擬企業(yè)間知識(shí)轉(zhuǎn)移主體的行為，構(gòu)建知識(shí)轉(zhuǎn)移行為的動(dòng)態(tài)演化博弈模型；蔣樟生等[14]建立了技術(shù)創(chuàng)新聯(lián)盟知識(shí)轉(zhuǎn)移決策的主從博弈模型，指出聯(lián)盟存在和發(fā)展的前提條件是盟主企業(yè)的知識(shí)邊際收益足夠大；董廣茂等[15]構(gòu)建知識(shí)轉(zhuǎn)移博弈模型，分析競(jìng)爭(zhēng)條件下知識(shí)轉(zhuǎn)移戰(zhàn)略及決定因素；陳果等[16]考慮只是發(fā)送方的風(fēng)險(xiǎn)態(tài)度為私有信息，利用演化博弈分析知識(shí)發(fā)送方風(fēng)險(xiǎn)態(tài)度披露策略和知識(shí)接收方信息處理策略的演化均衡，以及對(duì)知識(shí)轉(zhuǎn)移的影響。

總結(jié)國(guó)內(nèi)外研究文獻(xiàn)發(fā)現(xiàn)，學(xué)者們多從宏觀的角度出發(fā)，分析如何通過(guò)知識(shí)轉(zhuǎn)移策略的選擇實(shí)現(xiàn)知識(shí)轉(zhuǎn)移收益最大化，但很少深入探究合作雙方具體怎樣控制自身的知識(shí)轉(zhuǎn)移投入才能獲得最大收益。

知識(shí)轉(zhuǎn)移是一個(gè)動(dòng)態(tài)的過(guò)程，因而轉(zhuǎn)移雙方如何根據(jù)需要實(shí)現(xiàn)對(duì)知識(shí)轉(zhuǎn)移投入的動(dòng)態(tài)控制顯得尤為重要。目前動(dòng)態(tài)控制已被學(xué)者們應(yīng)用于多領(lǐng)域的研究[18-31]，但在知識(shí)轉(zhuǎn)移方面還鮮有涉及。Haurie等[17]學(xué)者構(gòu)建了兩生物種群的動(dòng)態(tài)控制沖突模型，通過(guò)改變控制變量影響雙方的生物捕獲量，解決生物種群的捕獲收益問(wèn)題。組織知識(shí)的演化具有明顯的生態(tài)系統(tǒng)特征。在產(chǎn)學(xué)研合作中，高校和企業(yè)則可以通過(guò)改變知識(shí)轉(zhuǎn)移投入影響雙方的知識(shí)轉(zhuǎn)移量，解決產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移的收益問(wèn)題。

因此。本文借鑒已有的知識(shí)轉(zhuǎn)移相關(guān)研究成果，結(jié)合產(chǎn)學(xué)研合作的特點(diǎn)，在Haur等學(xué)者[17]動(dòng)態(tài)控制沖突模型的基礎(chǔ)上，建立產(chǎn)學(xué)研合作中的知識(shí)轉(zhuǎn)移動(dòng)態(tài)控制模型。與以往研究不同之處，本文嘗試將動(dòng)態(tài)控制的思想引入到產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移中，并定量分析高校和企業(yè)調(diào)節(jié)知識(shí)轉(zhuǎn)移控制投入以持續(xù)獲取最大收益的不同路徑，為產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移提供理論借鑒。

2 模型構(gòu)建

2.1 基本假設(shè)

假設(shè)1：某高校和企業(yè)同屬于一個(gè)產(chǎn)學(xué)研合作系統(tǒng)，高校是知識(shí)的輸出方，企業(yè)是知識(shí)的接收方。在t時(shí)刻，高校的知識(shí)產(chǎn)出量為x1(t)，企業(yè)的知識(shí)吸收量為x2(t)。

假設(shè)2：高校知識(shí)產(chǎn)出量的自然增長(zhǎng)率為ε1，企業(yè)知識(shí)吸收量的自然增長(zhǎng)率為ε2，二者都是在沒有外界環(huán)境制約下各主體內(nèi)部行為引起的變化。

假設(shè)3：高校的知識(shí)產(chǎn)出量受到知識(shí)產(chǎn)出基礎(chǔ)設(shè)施、知識(shí)水平、知識(shí)轉(zhuǎn)移能力等資源的制約，不可能無(wú)限增大，因此假設(shè)其受到的資源限制水平為r11。同理，企業(yè)的知識(shí)吸收量受到知識(shí)吸收基礎(chǔ)設(shè)施、知識(shí)吸收能力等資源的制約，記企業(yè)的資源限制水平為r22。

假設(shè)4：由于同處于一個(gè)產(chǎn)學(xué)研合作系統(tǒng)，作為知識(shí)產(chǎn)出方的高校和作為知識(shí)吸收方的企業(yè)組成了知識(shí)轉(zhuǎn)移的鏈條，這種鏈條形成了高校和企業(yè)間相互補(bǔ)充、相互促進(jìn)的共生關(guān)系。高校和企業(yè)之間合作的契合度、交流的頻繁度等都會(huì)影響雙方的共生關(guān)系。記企業(yè)對(duì)高校的共生作用系數(shù)為r21，高校對(duì)企業(yè)的共生作用系數(shù)為r12。

假設(shè)5：高校可以通過(guò)控制對(duì)知識(shí)產(chǎn)出的投入來(lái)控制自身的知識(shí)產(chǎn)出量，也可以通過(guò)控制對(duì)知識(shí)轉(zhuǎn)移的投入來(lái)影響企業(yè)的知識(shí)吸收量。記高校對(duì)知識(shí)產(chǎn)出的控制投入為u1，它是高校對(duì)自身知識(shí)產(chǎn)出的控制變量；記高校對(duì)知識(shí)轉(zhuǎn)移的控制投入為u2，它是高校對(duì)企業(yè)知識(shí)吸收的控制變量。

假設(shè)6：作為產(chǎn)學(xué)研合作主體，高校產(chǎn)出知識(shí)需要企業(yè)的資助，所以企業(yè)可以通過(guò)控制對(duì)高校的投入來(lái)控制高校的知識(shí)產(chǎn)出量。同時(shí)，企業(yè)吸收知識(shí)也需要一定的投入，企業(yè)可以通過(guò)控制對(duì)知識(shí)吸收的投入來(lái)控制自身的知識(shí)吸收量。記企業(yè)對(duì)高校知識(shí)產(chǎn)出的控制投入為v1，它是企業(yè)對(duì)高校知識(shí)產(chǎn)出的控制變量；記企業(yè)對(duì)知識(shí)吸收的控制投入為v2，它是企業(yè)對(duì)自身知識(shí)吸收的控制變量。

2.2 知識(shí)轉(zhuǎn)移動(dòng)態(tài)控制模型建立

根據(jù)以上假設(shè)建立產(chǎn)學(xué)研知識(shí)轉(zhuǎn)移的動(dòng)態(tài)控制模型為：

(1)

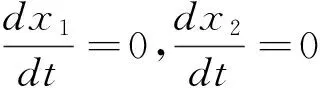
2.3 高校和企業(yè)目標(biāo)函數(shù)計(jì)算

企業(yè)在此段時(shí)間所獲取的目標(biāo)收益合計(jì)為：

3 知識(shí)轉(zhuǎn)移合作博弈求解

獲得經(jīng)濟(jì)利益是產(chǎn)學(xué)研合作各方參與合作的主要?jiǎng)恿εc目的[19]。為了獲得更大利益，高校和企業(yè)會(huì)采取聯(lián)合的方式，使產(chǎn)學(xué)研合作系統(tǒng)中的資源得到最優(yōu)配置，以謀求整體利益最大化，并在整體利益最大化的基礎(chǔ)上進(jìn)行利益分配，從而達(dá)到共贏。高校和企業(yè)通過(guò)調(diào)整各自的知識(shí)轉(zhuǎn)移投入實(shí)現(xiàn)共贏的過(guò)程，也是雙方合作博弈的過(guò)程。當(dāng)高校和企業(yè)進(jìn)行合作博弈時(shí)追求的是產(chǎn)學(xué)研合作整體利益最大化。

這時(shí)高校和企業(yè)選擇的控制策略可以歸結(jié)為一個(gè)標(biāo)準(zhǔn)：

P(u,v)=P1(u,v)+P2(u,v)

其中共軛變量λ1和λ2滿足方程組：

(2)

邊界條件λ1(T)=λ2(T)=0。

采用極大值原則解決這一問(wèn)題時(shí)，雙方優(yōu)化控制的條件為：

由此得到優(yōu)化控制的計(jì)算公式：

(3)

(4)

將得到優(yōu)化控制的計(jì)算公式(3)、(4)帶入動(dòng)態(tài)控制模型(1)得到方程組：

(5)

其中λ1和λ2由(2)和(5)組成的下列微分方程組：

(6)

求得。初始—邊界條件為：

不等式：

P(u*(t),v*(t))≥P(u(t),v(t))

對(duì)任何對(duì)手允許的程序控制成立。所以：

P(u*(t),v*(t))=P1(u*(t),v*(t))+P2(u*(t),v*(t))≥P1(u0(t),v0(t))+P2(u0(t),v0(t))

其中(u*(t),v*(t))是Nash均衡狀態(tài)。將微分方程組(6)求得的解代入到(3)、(4)算出該Nash均衡態(tài)的值，即高校和企業(yè)獲取最大整體利益時(shí)的納什均衡投入。

4 仿真分析

4.1 初始參數(shù)設(shè)置

表1 仿真參數(shù)賦值

4.2 投入的影響

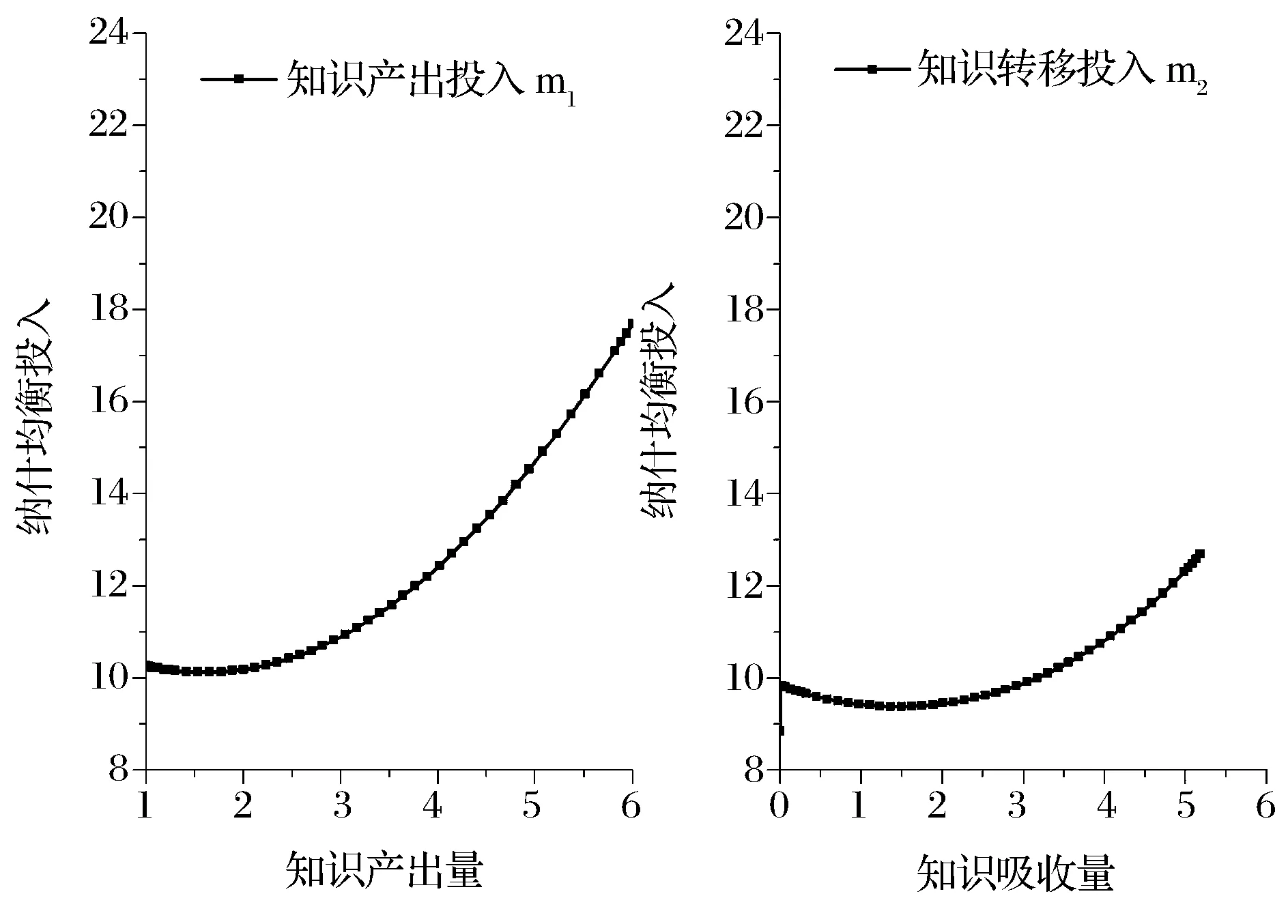
圖1 投入隨知識(shí)產(chǎn)出量和知識(shí)吸收量的變化關(guān)系

圖2 最優(yōu)獲利能力隨時(shí)間的變化關(guān)系

4.3 共生作用系數(shù)的影響

圖3(a) 共生作用系數(shù)對(duì)總投入的影響

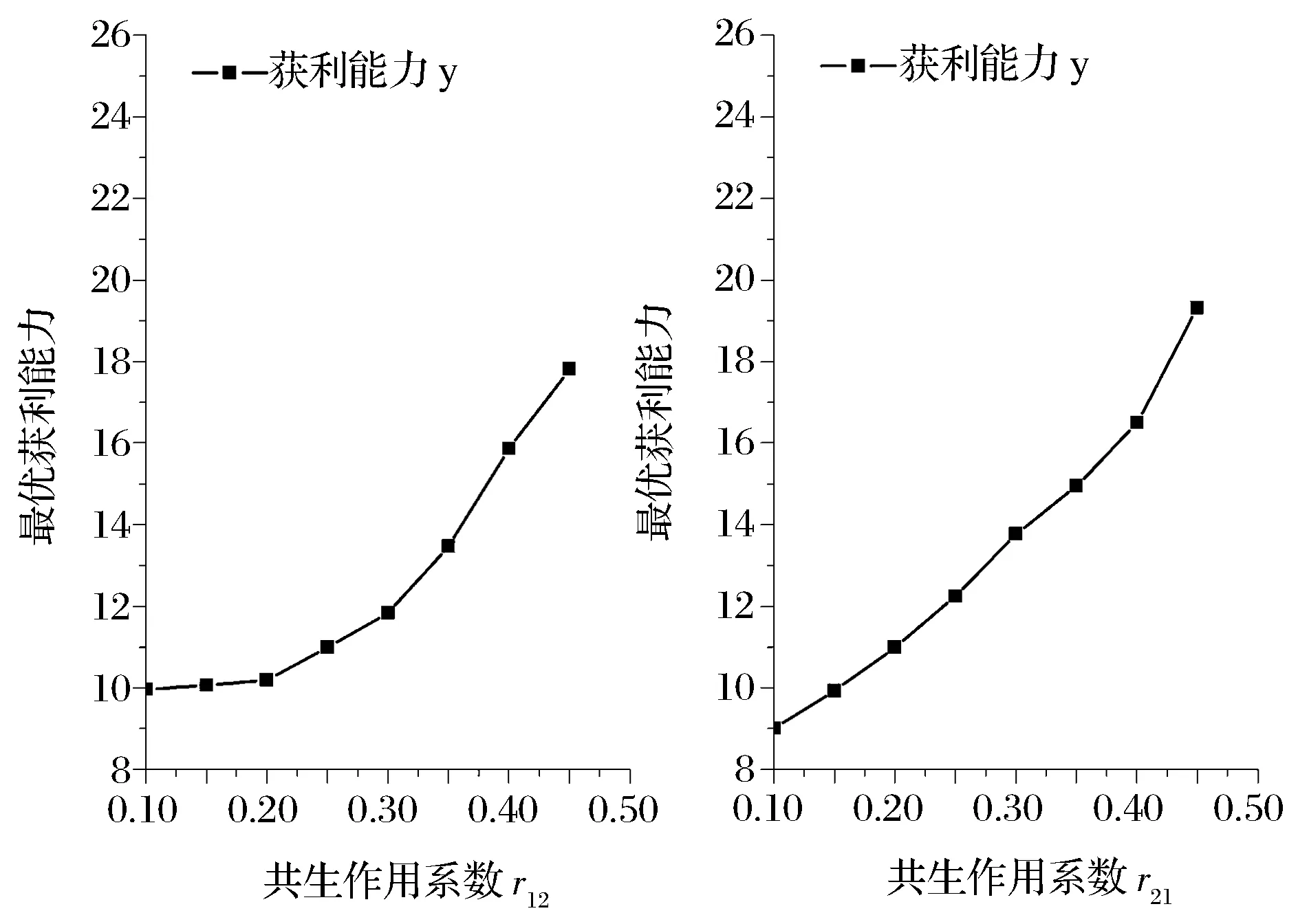
圖3(b) 共生作用系數(shù)對(duì)獲利能力的影響

4.3 資源限制水平的影響

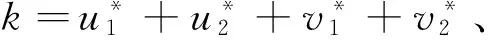
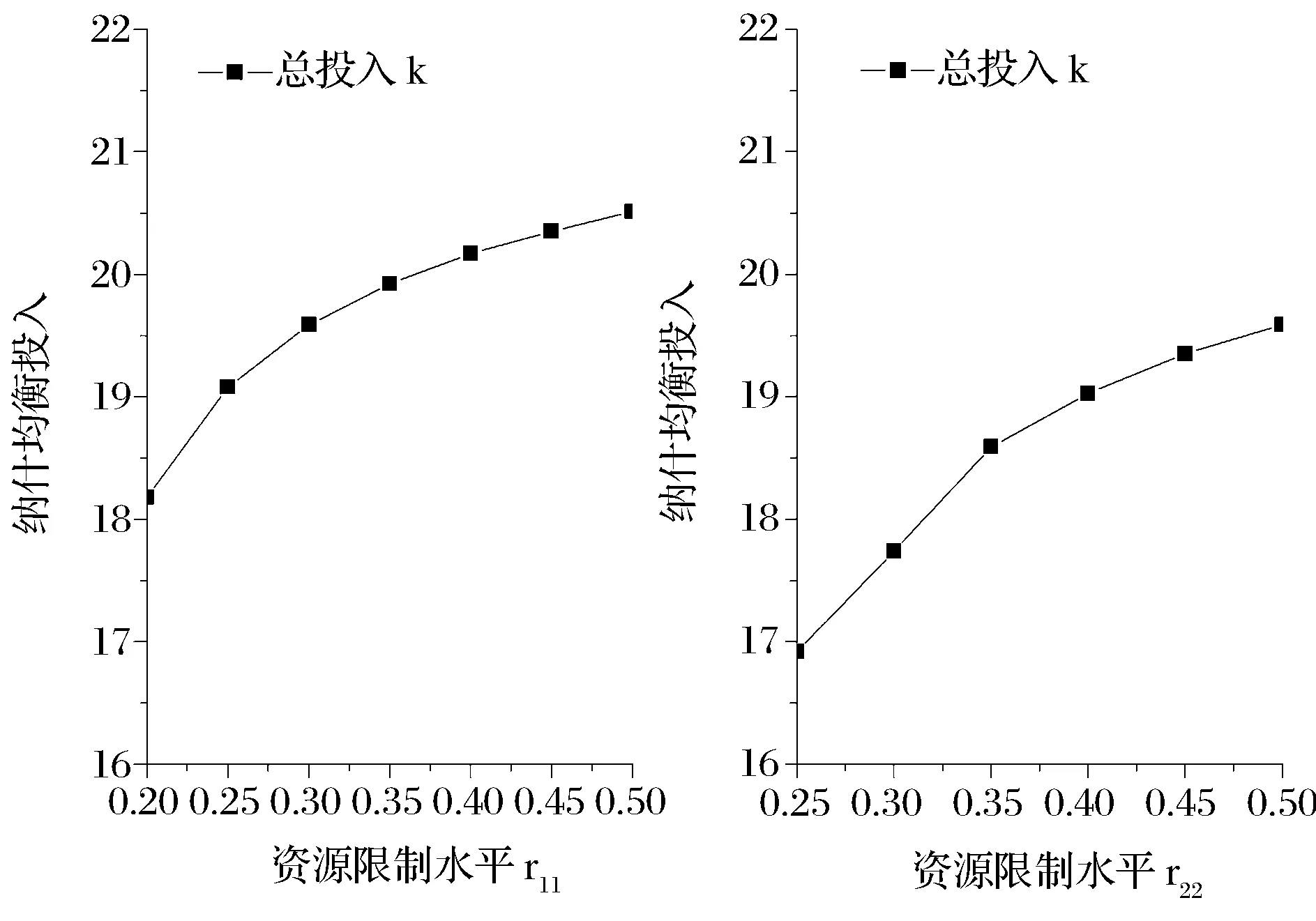
圖4(a) 資源限制水平對(duì)總投入的影響

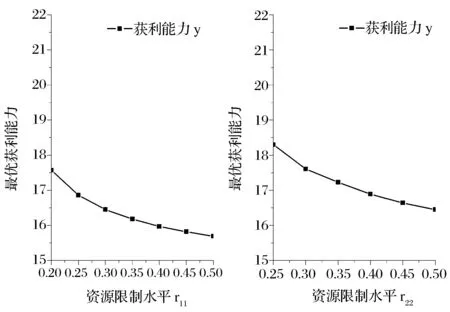
圖4(b) 資源限制水平對(duì)總投入的影響

5 結(jié)語(yǔ)

本文運(yùn)用博弈論研究了產(chǎn)學(xué)研合作中的知識(shí)轉(zhuǎn)移問(wèn)題，并將高校和企業(yè)作為兩個(gè)控制體，建立了產(chǎn)學(xué)研聯(lián)盟中的知識(shí)轉(zhuǎn)移動(dòng)態(tài)控制模型，構(gòu)造了高校和企業(yè)獲取收益的目標(biāo)函數(shù)。運(yùn)用納什均衡理論和哈密頓函數(shù)求得了高校和企業(yè)在合作博弈狀態(tài)下獲取最大收益時(shí)的納什均衡投入，探究了納什均衡投入與知識(shí)產(chǎn)出量和知識(shí)吸收量的關(guān)系及資源限制水平、共生系數(shù)變動(dòng)下納什均衡投入和單位投入最優(yōu)獲利能力的變化情況。模擬分析表明，高校和企業(yè)可以根據(jù)當(dāng)前產(chǎn)學(xué)研合作系統(tǒng)內(nèi)的知識(shí)產(chǎn)出量和吸收量來(lái)控制對(duì)知識(shí)產(chǎn)出和知識(shí)吸收的投入，從而影響產(chǎn)學(xué)研的最優(yōu)獲利能力；通過(guò)提高高校和企業(yè)間的共生作用或者降低資源限制水平均可降低產(chǎn)學(xué)研的納什均衡投入，提高其利潤(rùn)獲取能力。

鑒于此，高校和企業(yè)在產(chǎn)學(xué)研合作的過(guò)程中，應(yīng)該根據(jù)當(dāng)前合作系統(tǒng)中的知識(shí)產(chǎn)出量和吸收量隨時(shí)調(diào)整控制投入，以保持產(chǎn)學(xué)研的獲利能力在較高水平。另外，在產(chǎn)學(xué)研合作的過(guò)程中，高校和企業(yè)應(yīng)建立廣泛的聯(lián)系，加強(qiáng)雙方間的相互交流，提高雙方間的合作默契度，從而充分利用雙方間的共生影響作用。同時(shí)應(yīng)提高自身學(xué)習(xí)能力、消化吸收能力，建立完善的知識(shí)轉(zhuǎn)移基礎(chǔ)設(shè)施，如技術(shù)和網(wǎng)絡(luò)設(shè)施等，從而增強(qiáng)產(chǎn)學(xué)研合作的利潤(rùn)獲取能力。

[1] 曹霞,劉國(guó)巍.基于社會(huì)資本的產(chǎn)學(xué)研合作創(chuàng)新超網(wǎng)絡(luò)分析[J].管理評(píng)論,2013,25(4):115-124.

[2] Khan Z, Shenkar O, Lew Y K. Knowledge transfer from international joint ventures to local suppliers in a developing economy[J]. Journal of International Business Studies, 2015, 46(6):112.

[3] 劉芳.社會(huì)資本對(duì)產(chǎn)學(xué)研合作知識(shí)轉(zhuǎn)移績(jī)效影響的實(shí)證研究[J].研究與發(fā)展管理,2012,24(1):103-111.

[4] 曹霞,于娟,張路蓬.不同聯(lián)盟規(guī)模下產(chǎn)學(xué)研聯(lián)盟穩(wěn)定性影響因素及演化研究[J].管理評(píng)論,2016,28(2):3-14.

[5] Lai J, Lui S S, Tsang E W K. Intrafirm knowledge transfer and employee innovative behavior: the role of total and balanced knowledge flows[J]. Journal of Product Innovation Management, 2015,33(1):90-103.

[6] 高麗坤,艾時(shí)鐘.企業(yè)間知識(shí)轉(zhuǎn)移的泄密問(wèn)題研究[J].中國(guó)管理科學(xué),2015,23(S1):364-369.

[7] Lin Lihui, Geng Xianjun, Whinston A B. A sender-receiver framework for knowledge transfer[J]. MIS quarterly, 2005,29(2): 197-219.

[8] 李洋,劉偉.基于演化博弈理論的軟件隱形需求開發(fā)研究[J].系統(tǒng)管理學(xué)報(bào),2015,24(4):480-495.

[9] Jiang Zhangsheng, Hao Yunhong. Game analysis of technology innovation alliance stability based on knowledge transfer [J]. Computational & Mathematical Organization Theory, 2013, 19(4):403-421.

[10] Li Y M,Li J H. Knowledge sharing in communities of practice: A game theoretic analysis [J]. European Journal of Operational Research, 2010, 207(2):1052-1064.

[11] Bandyopadhyay S, Pathak P.Knowledge sharing and cooperation in outsourcing projects——A game theoretic analysis[J]Decision Support Systems,2007,43 (2):349-358.

[12] Szulanski G, Ringov D, Jensen R J. Overcoming stickiness: How the timing of knowledge transfer methods affects transfer difficulty[J]. Organization Science, 2016, 27(2): 304-322.

[13] 許學(xué)國(guó),梅冰青,吳耀威.跨國(guó)公司-代工企業(yè)知識(shí)轉(zhuǎn)移主體行為研究[J].經(jīng)濟(jì)與管理研究,2016,37(4):119-126.

[14] 蔣樟生,胡瓏瑛.技術(shù)創(chuàng)新聯(lián)盟知識(shí)轉(zhuǎn)移決策的主從博弈分析[J].科研管理,2012,33(4):41-47+61.

[15] 董廣茂,林敏,雷宏振. 競(jìng)爭(zhēng)條件下企業(yè)知識(shí)轉(zhuǎn)移戰(zhàn)略及其對(duì)產(chǎn)業(yè)演化的影響[J].管理學(xué)報(bào),2014,11(8):1246-1252.

[16] 陳果,齊二石.風(fēng)險(xiǎn)態(tài)度不成對(duì)下的企業(yè)間知識(shí)轉(zhuǎn)移研究[J].中國(guó)管理科學(xué),2016,24(12):82-90.

[17] Haurie A, Krawczyk J. An introduction to dynamic games [M].2000.

[18] Chen K, Xiao Tiaojun. Ordering policy and coordination of a supply chain with two-period demand uncertainty[J]. European Journal of Operational Research, 2011, 215(2): 347-357.

[19] Hamdouch Y Multi-period supply chain network equilibrium with capacity constraints and purchasing strategies[J].Transportation Research, Part C, 2011, 19(5): 803-820.

[20] Dong F, Deglise-Hawkinson J R, Van Oyen M P, et al. Dynamic control of a closed two-stage queueing network for outfitting process in shipbuilding [J]. Computers & Operations Research,2016.72：1-11.

[21] Liu Zugang, Nagurney A. Multiperiod competitive supply chain networks with inventorying and a transportation network equilibrium reformulation [J].Optimization and Engineering, 2012, 13(2): 471-503.

[22] Venayak N, Anesiadia N, Cluett W R, et al. Engineering metabolism through dynamic control[J].Current Opinion in Biotechnology,2015,34:142-152.

[23] Antonelli M, Baccioli A, Francesconi M, et al. Dynamic modelling of a low-concentration solar power plant: A control strategy to improve flexibility [J]. Renewable Energy,2016.95：574-585.

[24] Su Zhilong, Li Xiaokang, Jiang Xuesong, et al. Dynamic control of the location of nanoparticles in hybrid co-assemblies[J]. Nanoscale, 2015, 7(12):5262-9.

[25] 黃孝鵬,周獻(xiàn)中.復(fù)雜決策任務(wù)層級(jí)分解動(dòng)態(tài)控制策略與算法[J].軍事運(yùn)籌與系程,2013,27(1): 71-75.

[26] 李恒,張友安,孫富春,等.多操縱面飛機(jī)全局集合穩(wěn)定非線性自適應(yīng)動(dòng)態(tài)控制分配[J].控制與決 策,2013,28(3):379-390.

[27] 彭蘭梅.施工進(jìn)度計(jì)劃的動(dòng)態(tài)控制在高速公路改造工程中的應(yīng)用[J].中外公路,2013,33(5):349-351.

[28] 謝文博,付明玉,施小成.一類非線性系統(tǒng)的加速度規(guī)劃輸出跟蹤動(dòng)態(tài)控制[J].控制理論與應(yīng)用,2013,27(1):71-75.

[29] Huang Jiajiang, Liu Xin, Li Dan, et al. Dynamic control of enhancer repertoires drives lineage and stage-specific transcription during hematopoiesis[J]. Developmental cell, 2016, 36(1): 9-23.

[30] Ferrer P, Castillo-Neyra R, Roy C N, et al. Dynamic control of hepatic Plasmodium numbers by hepcidin despite elevated liver iron during iron supplementation[J]. Microbes and Infection, 2016, 18(1): 48-56.

[31] Kamimura M, Sugawara M, Yamamoto S, et al. Dynamic control of cell adhesion on a stiffness-tunable substrate for analyzing the mechanobiology of collective cell migration[J]. Biomaterials science, 2016, 4(6): 933-937.

Research on Knowledge Transfer Cooperative Game in University-Industry Cooperation Based on Dynamic Control Model

WU Jie1， PENG Xing-xing1， SHENG Yong-xiang1，LI Peng1，SHI Qin-fen2

(1.Economics & Management School, Jiangsu University of Science and Technology, Zhenjiang 212003,China；2.Office of Science & Technology, Nanjing University of Posts and Telecommunications, Nanjing 210003,China)

In the collaboration practice among industry, universities and research institutes, universities and enterprises can influence the amount of knowledge of both sides by changing the knowledge transfer input to resolve the problem of income among industry, universities and research institutes. Universities’ knowledge output and enterprises’ absorptive amount can be affected at time, natural growth rate, restriction level of resource, symbiotic relationship, partner’s behaviour and self behavior. In this paper, adjustments of knowledge transfer input for universities and enterprises to pursue their own maximum interest are analyzed through building dynamic control model. the objective function is calcucated, the equilibrium of cooperative game in knowledge transfer is solved and a simulation analysis in made. In this model, universities and enterprises are the control subjects. They pursue their own maximum interest by adjusting the investment of knowledge transfer. Based on the method of calculating the dynamic control model, the initial value of model parameter is gotten through the empirical research and makes a simulation. Simulation results show that universities and enterprises can adjust the investment according to the knowledge output and knowledge absorption in the system, and then affect the optimal profit ability of industry, universities and research institutes.The increase of the symbiotic effect coefficient and decrease of resource constraints levels is helpful to minimize the Nash equilibrium input and maximize the optimal profit ability. in view of this, In the process of "industry-university-institute" cooperation, universities and enterprises should adjust the investment at any time according to the knowledge output and knowledge absorption in the system to maintain production profitability at a higher level. In addition, in the process of "industry-university-institute" cooperation, universities and enterprises shall establish extensive connection, strengthen mutual exchanges between the two sides, improve the tacit understanding degree and make full use of the symbiotic effect between the two sides.

knowledge transfer; university-industry cooperation; dynamic control model; cooperative game

1003-207(2017)03-0190-07

10.16381/j.cnki.issn1003-207x.2017.03.022

2015-05-28；

2016-05-21

國(guó)家社科基金重點(diǎn)資助項(xiàng)目(14AGL001)；國(guó)家自然科學(xué)基金資助項(xiàng)目(71271119，71401064，71471091)

吳潔(1968-)，女(漢族)，江蘇濱海人，江蘇科技大學(xué)經(jīng)濟(jì)管理學(xué)院，教授，研究方向：知識(shí)轉(zhuǎn)移、技術(shù)創(chuàng)新，E-mail:0511wujie@163.com.

F224.32；F272

A