考慮電流諧波的永磁同步電機電磁振動和噪聲半解析模型

林 福 左曙光 毛 鈺 吳雙龍 鄧文哲

(同濟大學新能源汽車工程中心 上海 201804)

?

考慮電流諧波的永磁同步電機電磁振動和噪聲半解析模型

林 福 左曙光 毛 鈺 吳雙龍 鄧文哲

(同濟大學新能源汽車工程中心 上海 201804)

提出了一種永磁同步電機快速半解析計算模型，可以分析常見的電流諧波對振動和噪聲的影響，并提高了計算效率。首先通過解析和有限元相結合的方法計算了永磁體磁通密度和氣隙比磁導，并建立了考慮任意電流波形的電樞磁通密度的解析模型，通過麥克斯韋應力張量方程計算徑向電磁力，與有限元計算的電磁力吻合較好。其次通過二維傅里葉變換得到了特定空間階數電磁力的頻率成分，并基于殼體振動和聲輻射模型分別計算了定子表面振動和噪聲，計算結果能夠反映實測振動噪聲的主要峰值和分布。最后分析了電流諧波引起的振動噪聲的階次特征和峰值變化。該文提出的半解析模型為在設計階段考慮電機的振動和噪聲提出了一種有效分析方法。

永磁同步電機 電磁力 振動和噪聲預測 電流諧波 半解析模型 二維分解

0 引言

近幾年來，永磁同步電機的振動和噪聲問題得到了越來越廣泛的關注，電機運行過程中由電磁力激發的電磁噪聲是電機噪聲的主要來源[1]。尤其是分數槽集中繞組永磁同步電機，相比于整數槽電機，其電磁力空間階數更低，電磁振動和噪聲問題更加突出[2-5]。在低噪聲應用領域，噪聲大小已成為評價電機性能的重要指標。

永磁同步電機的振動和噪聲分析涉及電磁場、電磁力、結構振動和聲輻射等多物理場研究，目前關于振動和噪聲建模方面可以歸納為解析和數值兩類。文獻[6]建立了二維平面內的電機振動模型，雖然能夠快速計算定子振動，但忽略了定子齒、繞組等復雜結構，而且不能考慮端蓋約束對結構的影響，因而解析模型很難反映電機定子實際的振動情況。在振動噪聲數值預測方面，文獻[7]首先通過力錘施加脈沖激勵獲取定子結構的傳遞特性，再將電磁力加載到齒中心處計算了結構表面的振動。文獻[8]建立了開關磁阻電機的多物理場數值預測模型(包括電路、電磁力、振動和聲學模型)，能夠較好地反映出噪聲的主要峰值和總體趨勢。但文獻[7，8]都忽略了電磁力沿定子表面的不均勻分布，將一個齒距內的電磁力積分后等效到齒中心，類似的電磁力等效方法也出現在文獻[9，10]中，這種力的加載方式忽略了電磁力沿定子齒表面的非均勻分布，增加振動和噪聲計算的誤差。文獻[11]首先通過電磁脈沖響應獲取了開關磁阻電機定子結構的固有特性；其次由電機振動測試提取結構表面一些點的振動,再通過模態擴展的方法獲取了整個定子表面的振動;最后通過聲學邊界元法計算了聲輻射。噪聲計算結果能夠反映實測噪聲的主要峰值，但采用該計算方法需要事先通過試驗獲取結構表面一些點的振動。逆變器供電下，電流諧波是電機運行過程中常見的影響因素[12]。文獻[13]通過有限元模型分析了電流諧波對盤式電機噪聲的影響，指出逆變供電下的噪聲比理想正弦波條件下的噪聲高約10 dB。文獻[14，15]通過采集實測電流，分別通過場重建法和有限元方法計算了振動和噪聲響應，但都未指出電流諧波引起的振動和噪聲的階次特征和峰值變化。

本文基于殼振動和聲輻射理論提出了一種快速半解析計算模型來預測定子表面振動和噪聲，通過對徑向電磁力進行二維分解，考慮不同空間分布的電磁力對振動和噪聲的貢獻。此外建立了考慮任意電流波形的電磁力半解析計算模型，能夠分析電機運行過程中常見的電流諧波對振動和噪聲的影響。具體建模流程如圖1所示，首先通過解析和有限元相結合的方法計算永磁體磁通密度和氣隙比磁導，由解析模型計算任意電流波形下的電樞磁通密度。其次通過麥克斯韋應力張量方程計算徑向電磁力的時空分布，由二維傅里葉變換得到特定空間階數電磁力的頻率成分。然后通過三維有限元模態分析得到定子的模態參數，并基于圓柱殼振動理論計算不同空間階數電磁力激發的電磁振動。最后由邊界元方法計算定子的模態輻射效率，并結合殼體聲輻射模型計算定子輻射噪聲，通過振動和噪聲試驗對計算結果進行驗證。

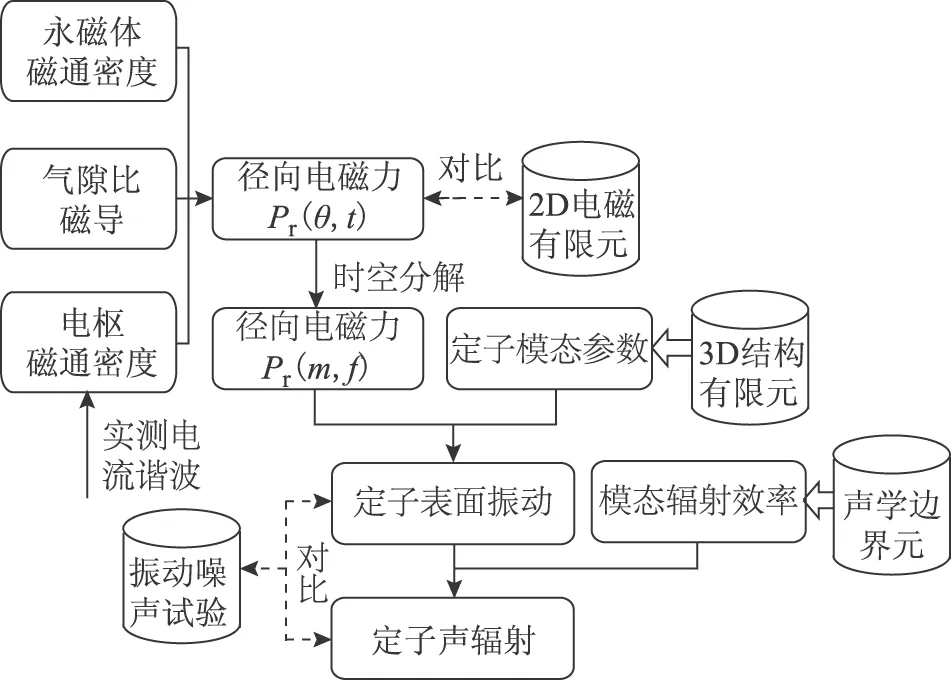
圖1 永磁同步電機振動和噪聲半解析預測流程Fig.1 Semi-analytical prediction procedure of vibration and noise for PMSM

1 徑向電磁力建模與時空分解

在永磁同步電機中氣隙磁場包含永磁體產生的磁場和繞組通電后產生的電樞反應磁場，而定子開槽則影響氣隙磁場的空間分布，通常通過引入氣隙比磁導系數加以考慮。在忽略磁路飽和的條件下，氣隙磁通密度等于永磁體磁通密度加上電樞磁通密度再乘以開槽引入的比磁導，即

brs=(Br_mag+Br_arm)λr

(1)

式中，Br_mag、Br_arm分別為徑向永磁體磁通密度和電樞磁通密度；λr為比磁導實部。

1.1 永磁體磁通密度和氣隙比磁導

對于瓦片形表貼式永磁電機，永磁體磁通密度可通過文獻[16，17]的解析模型獲得，然而本文研究的6極9槽電機的永磁體并不是規整的瓦片形，具體結構如圖2所示，電機的主要參數見表1。但該電機的永磁體磁通密度仍可以通過傅里葉級數表示，即

(2)

式中，θ為空間角度；t為時間；p為極對數；f1為電流基波頻率；Bmn為n次永磁體磁通密度諧波幅值，通過靜磁場有限元分析得到。

開槽引起的氣隙比磁導可以通過求解文獻[18]中的復數域內的非線性方程獲取，然而該方程求解較為困難，本文通過解析和有限元相結合的方式求解比磁導。借助復數比磁導，當考慮徑向和切向磁通密度的相互貢獻時，開槽下的徑向和切向永磁體磁通密度可表示為

Brs_mag=Br_magλr+Bt_magλt

(3)

Bts_mag=Bt_magλr-Br_magλt

(4)

式中，Bt_mag為未考慮開槽的永磁體切向磁通密度；λt為比磁導虛部。首先通過靜磁場有限元分析得到Brs_mag、Bts_mag、Br_mag和Bt_mag，再根據式(3)和式(4)求解λr。

圖2 6極9槽電機結構Fig.2 Structure of the motor with 6 poles and 9 slots

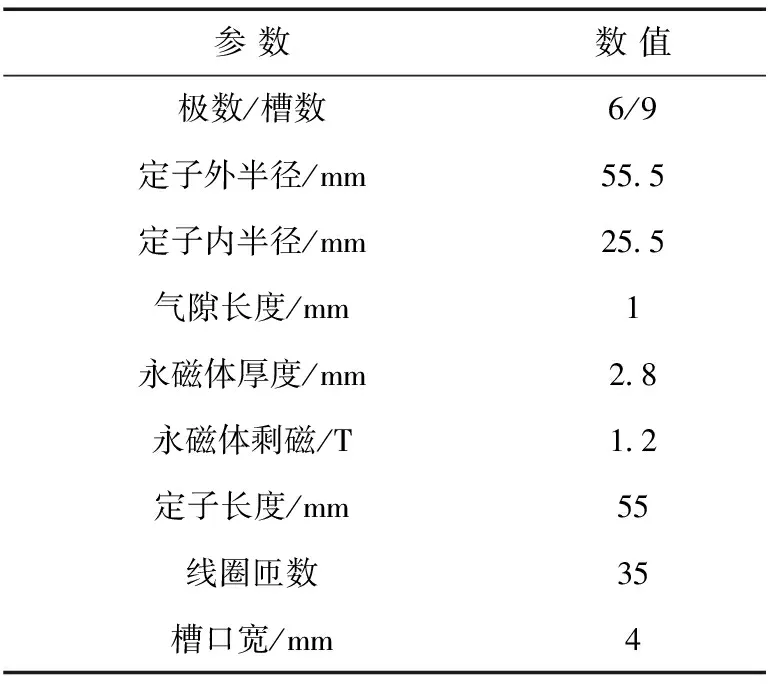
表1 電機主要參數

1.2 考慮電流諧波的電樞磁通密度計算

單匝線圈施加單位電流產生的徑向氣隙磁通密度可表示為

(5)

式中，Bcv可以通過文獻[19]的解析模型得到。

對于6極9槽這一類單元電機極槽數相差1的雙層繞組電機，A相繞組產生的徑向磁通密度可表示為

(6)

式中，IA(t)為A相線圈電流；Ns為定子匝數；Nt為單元電機數；kdv為繞組分布系數。

根據三相繞組的空間分布可以得到合成后的徑向電樞磁通密度為

(7)

式中，θBA和θCA分別為B相和C相繞組中心線超前A相繞組的機械角度，且θCA=2θBA，若繞組沿旋轉方向依次為A-B-C，則θBA=2π/(3Nt)；若繞組沿旋轉方向依次為A-C-B，則θBA=-2π/(3Nt)。

式(7)中的三相電流波形通過試驗獲取。圖3為轉速3 600 r/min、負載扭矩為2.7 N·m(額定工況)時的三相電流?？梢钥吹诫娏鳛榉钦也ㄐ?，對其進行頻譜分析，結果如圖4所示。從圖4中可以發現主要的電流諧波包括5次、7次和13次等(6k±1)次電流諧波以及以開關頻率fc(9 000 Hz)為中心的電流諧波，包括頻率為fc、fc±f1、fc±2f1和fc±4f1等諧波。

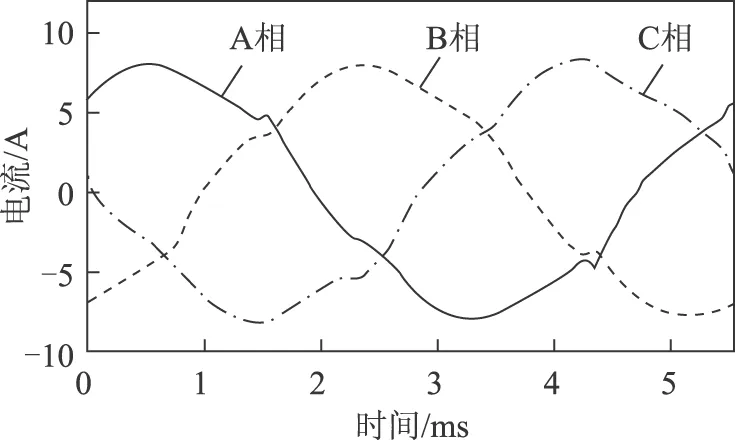
圖3 實測電流Fig.3 Tested current

圖4 A相電流頻譜Fig.4 Frequency spectrum of A-phase current

1.3 徑向電磁力計算及與有限元對比

將計算得到的Br_mag、Br_arm和λr帶入式(1)可以計算負載下的徑向氣隙磁通密度brs。根據麥克斯韋張量方程，徑向電磁力可表示為

(8)

式中，μ0為真空磁導率。

本文建立了二維電磁有限元模型來驗證半解析模型計算得到的電磁力，電機電磁有限元模型如圖5所示。由于該6極9槽電機在空間上相當于3個2極 3槽電機，因此只建立了1/3模型，將圖3所示的電流波形加載到有限元模型中作為電流源來計算徑向氣隙磁通密度，并根據式(8)計算徑向電磁力。圖6為半解析模型得到的電磁力與有限元得到的電磁力對比。從圖中可以看出兩者的結果吻合較好，說明了半解析模型的準確性，此外半解析模型的計算效率更高。

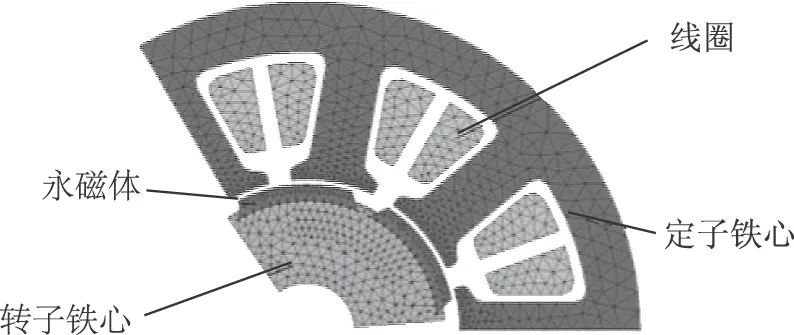
圖5 電機電磁有限元模型Fig.5 Electromagnetic FE model of motor

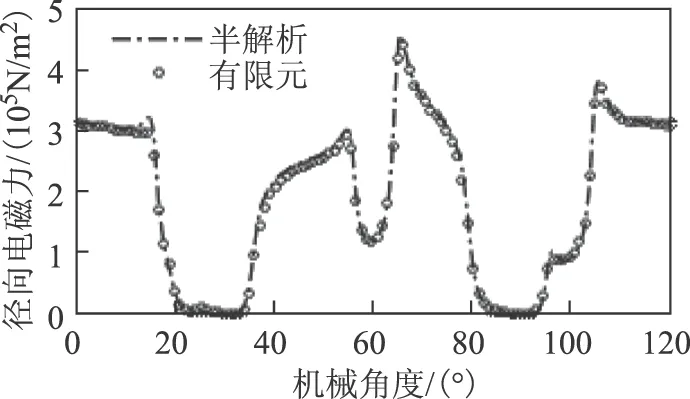
圖6 半解析與有限元計算的電磁力對比Fig.6 Contrast of electromagnetic force from semi-analytical model and FE simulation

1.4 徑向電磁力時空分解

電磁力具有空間分布和隨時間變化的特征，圖7為額定工況下的徑向電磁力的時空分布，諸多研究只是選取空間某一點的電磁力時間歷程進行時間諧波分析或選取某一時刻的電磁力空間分布進行空間諧波分析[6，7]，相當于只選取了圖7中的某個空間或者時間截面進行分析。這種一維的諧波分析方法不能同時結合電磁力的空間分布和旋轉頻率。文獻[20]指出只有當徑向電磁力的空間階數等于定子的徑向模態階數，且這一階徑向力波包含的頻率靠近對應階數的定子模態頻率時，電機才發生共振。因此簡單的一維徑向電磁力分解并不能很好地分析電機的振動和噪聲分布規律。

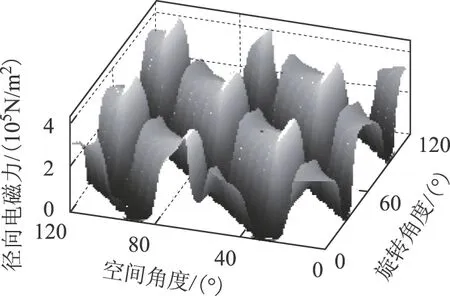
圖7 徑向電磁力時空分布Fig.7 Spatial and temporal distribution of radial force density

為了分析不同空間階數和不同頻率的電磁力對電機振動噪聲的貢獻，本文采用二維傅里葉變換對隨空間和時間變化的電磁力進行時空分解。圖8為轉矩為2.7 N·m時采用正弦電流和非正弦電流得到的徑向電磁力的諧波，圖中頻率的正負表示電磁力的旋轉方向，當其與轉子旋轉方向相同時為正，反之則為負。

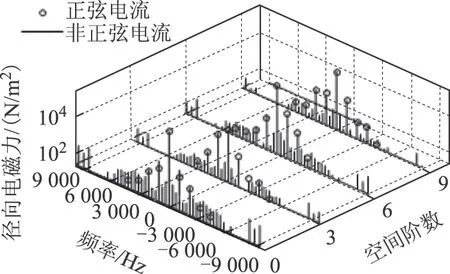
圖8 徑向電磁力時空分解Fig.8 Spatialandtemporal decomposition of radial force density

雙層繞組電機的徑向電磁力的空間階數為極槽數的最大公約數的整數倍，因此在6極9槽電機中，電磁力的空間階數為3的整數倍。對比正弦電流和非正弦電流下的電磁力諧波可以看到，電流諧波不引起額外的電磁力空間諧波，但極大地豐富了電磁力的頻率。電流諧波產生的幅值較大的電磁力來源于其產生的電樞磁場同永磁體基波磁場的作用。因此頻率為fh的電流諧波，其產生的主要電磁力頻率成分為fh±f1。由此可知，頻率為(6k±1)f1的電流諧波產生的電磁力頻率仍為電流基頻的偶數倍，與理想正弦波條件下的電磁力特征重合。而以開關頻率為中心分布的頻率為fc±af1(a為整數)的電流諧波產生的主要電磁力頻率為fc±(a±1)f1。

2 定子振動計算及驗證

2.1 定子有限元模態分析

本系統基于單總線EEPROM芯片DS2431設計eID方式的電子標簽，具有體積小、觸點少、可實時讀寫等優點。通過在光纖連接器上安裝eID標簽，在光纖熔配一體化托盤（以下簡稱光纖托盤）的活動連接器上安裝eID標簽插座，光纖托盤內部布放存有內部光纖連接信息的數據采集電路板，實現了對光纖托盤每路活動連接器兩端光纖信息的數據采集，從而實現了ODN的數字化和智能化管理。

通過模態疊加的方法計算定子表面振動，首先需要獲取定子的模態參數。基于殼或環理論的解析模型難以精確考慮齒、繞組等復雜因素對結構模態參數的影響，所以本文通過建立定子的有限元模型來計算定子的模態參數，如圖9所示。

圖9 定子有限元模型Fig.9 FE model of stator

由文獻[3]的分析可知，徑向電磁力激發的定子表面振動位移與空間階數的4次方呈反比，通常只考慮空間1～4階的電磁力對振動噪聲的貢獻。因此對于本文的6極9槽電機，空間3階電磁力對噪聲的貢獻是最主要的，所以定子3階模態的參與程度是最高的。通過有限元模態分析可以得到定子的3階模態參數，如圖10所示。由于定子表面切邊、定子開槽和繞線等原因，存在兩個近似圓周3階的模態。

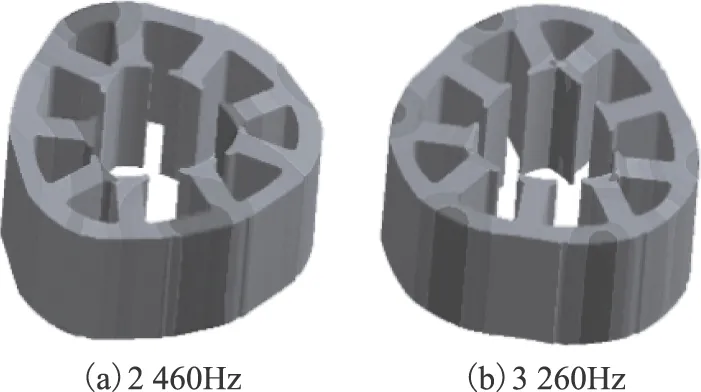
圖10 定子3階模態Fig.10 3rd mode of stator

2.2 定子表面振動計算及與試驗對比

基于圓柱殼振動理論[20]，空間m階徑向力波產生的m階振動位移幅值為

(9)

式中，Dsi為定子內直徑；M為定子質量；Prm為空間m階徑向力波幅值；fm為定子m階模態頻率；hm為結構放大因子，可表示為

(10)

式中，ξm為m階模態阻尼；f為m階電磁力頻率。模態阻尼采用文獻[20]中的經驗公式。

形如Prmcos(mθ±2πft+θm)的徑向電磁力產生的振動位移為Armcos(mθ±2πft+θm+φ)，加速度為4π2f2Armcos(mθ±2πft+θm+φ)，其中θm為m階電磁力相位，φ為結構阻尼導致的相位變化，如式(11)所示。

(11)

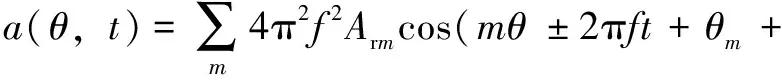
(12)

式(12)為不同空間階數、不同旋轉方向和頻率的電磁力引起的振動的統一表達式。在本文分析中，只考慮對振動噪聲貢獻最大的空間3階電磁力(m=3)引起的振動，而在結構方面，則考慮圖10所示的3階定子模態的參與。圖11為計算得到的額定工況下定子表面某點的振動與實測對應點振動的對比。從圖11中可以看出實測振動的主要頻率在半解析計算結果中都能得到體現，其中以開關頻率為中心存在幅值較大的頻率為fc、fc±f1、fc±2f1、fc±3f1和fc±5f1的振動，根據1.4節的分析，這些振動階次是由于開關頻率附近的電流諧波導致。而在中低頻段，振動的主要頻率為360 Hz的整數倍，即為電流基頻的偶數倍，其中在1 440 Hz和2 520 Hz處存在較大的振動峰值。由圖8可知，在1 440 Hz處的空間3階電磁力幅值為9 525 N/m2，電磁力幅值較大。而在2 520 Hz處，雖然空間3階電磁力幅值僅為68 N/m2，但其靠近頻率為2 460 Hz的模態，也能產生較大的振動。

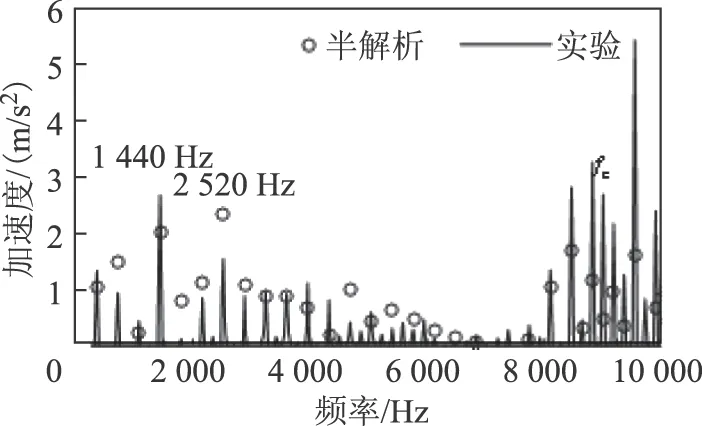
圖11 半解析計算振動與實測振動對比Fig.11 Contrast of vibration from semi-analytical model and test

3 定子輻射噪聲計算及驗證

3.1 模態輻射效率計算

m階模態輻射效率定義為[20]

(13)

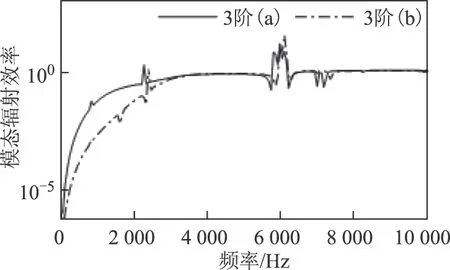
圖12 定子模態輻射效率Fig.12 Modal radiation efficiency of stator

3.2 定子輻射噪聲計算及試驗驗證

在定子表面振動位移Arm和定子模態輻射效率σm求解的基礎上可得到m階振動輻射的聲功率為

(14)

將各階振動貢獻的聲功率疊加后可以得到定子輻射的聲功率，轉換成聲功率級后可表示為

(15)

式中，wref為參考聲功率，wref=10-12W。

計算離電機較遠的遠場聲壓時，可近似將電機當成點聲源處理，此時離電機中心距離為R處的聲壓級為

LP=LW-20lgR-11

(16)

在電機噪聲試驗中，麥克風布置在電機垂直上方35cm處，圖13為額定工況下根據本文的半解析模型計算得到的聲壓級與實測聲壓級的對比。從圖13中可以看出噪聲主要能量的分布與振動類似，半解析計算結果和試驗結果都表明噪聲主要階次集中在360Hz的整數倍處以及開關頻率附近。中低頻段的實測噪聲峰值都能在半解析計算結果中得到體現，其中1 440Hz和2 520Hz的噪聲幅值最大，這兩個頻率處的半解析和實測結果差值分別為0.31dB(A)和3.6dB(A)，而在開關頻率附近，半解析與實測噪聲的幅值有一定誤差。在總聲級對比上，0～10 000Hz內的半解析和實驗得到的總聲級分別為55dB(A)和59.8dB(A)，兩者的差距主要是由于高頻噪聲計算的誤差導致。當只考慮0～6 000Hz以內的總聲級時，半解析和試驗結果分別為54.9dB(A)和56.8dB(A)，兩者較為接近。

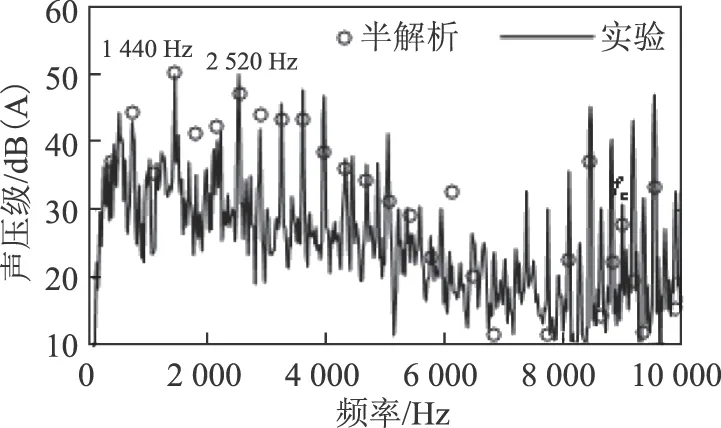
圖13 半解析計算噪聲與實測噪聲對比Fig.13 Contrast of noise from semi-analytical model and test

半解析模型計算的誤差來源包括以下方面：①定子外表面非理想的圓柱殼輻射面；②模態阻尼采用經驗阻尼，對共振處的計算精度影響較大；③實測低頻段(500Hz以內)的噪聲主要受機械噪聲的影響；④只考慮10 000Hz以內的定子徑向振動模態，存在模態截斷造成的誤差，尤其是針對高頻段的計算精度影響較大。

4 電流諧波對振動和噪聲的影響

進一步分析電流諧波對永磁同步電機電磁振動和噪聲的影響，圖14為基于本文的半解析模型得到的正弦電流和非正弦電流下的電磁振動和噪聲對比。從圖14中可以看到電流諧波對整個寬頻帶內的振動和噪聲都有一定的影響。

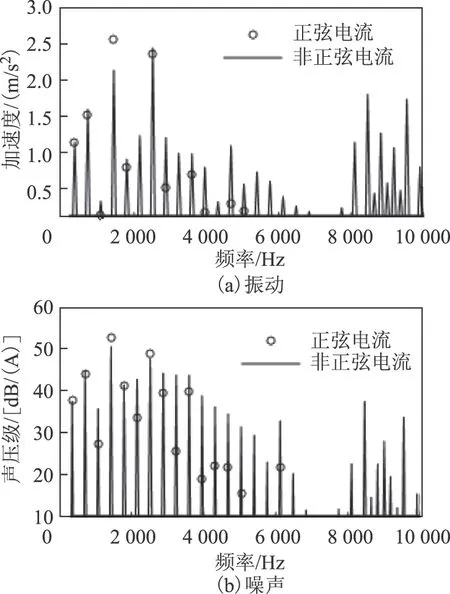
圖14 正弦電流和非正弦電流下的振動和噪聲對比Fig.14 Contrast of vibration and noise under sinusoidal current and nonsinusoidal current

首先以開關頻率為中心的頻率為fc、fc±f1、fc±2f1、fc±3f1和fc±5f1的振動和噪聲，這些是開關頻率附近的電流諧波產生的特有的階次特征。此外，雖然頻率為(6k±1)f1的電流諧波產生的電磁力頻率在額定工況下也集中在360 Hz的整數倍處，但其對振動噪聲的幅值有一定的影響。從圖14中可以看出主要的振動和噪聲階次在考慮電流諧波時，幅值都有一定的增加，然而在1 440 Hz處，正弦電流和非正弦電流下的振動幅值分別為2.55 m/s2和2.12 m/s2，聲壓級分別為52.54 dB(A)和50.39 dB(A)，可以看到電流諧波對該頻率下的振動噪聲有一定的削弱作用。這主要是由于電流諧波對該頻率下3階電磁力幅值的削弱作用，由圖8可以得到正弦波和非正弦波下1 440 Hz處的3階 電磁力幅值分別為1 211 N/m2和998 N/m2。

5 結論

1)建立了考慮任意電流波形下的徑向電磁力半解析模型，不僅能提高計算效率，而且能達到有限元計算的精度。

2)結合電磁力二維分解以及殼體振動和聲輻射模型建立了永磁同步電機電磁振動和噪聲的快速預測的半解析模型。該模型能夠反映實測結果的主要峰值，尤其是在中低頻段具有較高的計算精度，適用于在電機設計階段對電機振動和噪聲進行快速預估。

3)分析了電流諧波對振動和噪聲的影響，指出以開關頻率為中心分布的頻率為fc±af1(a為整數)的電流諧波產生頻率為fc±(a±1)f1的振動噪聲。而頻率為(6k±1)f1的電流諧波雖然產生的電磁力頻率與正弦波條件下的電磁力頻率重合，但其對振動噪聲幅值有一定的影響，具體的影響則取決于電流諧波對空間最低階電磁力幅值的影響。

[1] Magnussen F，Lendenmann H.Parasitic effects in PM machines withconcentrated windings[J].IEEE Transactions on Industry Applications，2007，43(5)：1223-1232.

[2] 左曙光，林福，孫慶，等.極槽配合和繞組層數對永磁同步電機振動的影響分析[J].振動與沖擊，2014，33(13)：130-134. Zuo Shuguang，Lin Fu，Sun Qing，et al.Vibration of permanent magnet synchronous motor with different slot-pole combinations and winding layers[J].Journal of Vibration and Shock，2014，33(13)：130-134.

[3] Verez G，Barakat G，Amara Y，et al.Impact of pole and slot combination on vibrations and noise of electromagnetic origins in permanent magnet synchronous motors[J].IEEE Transactions on Magnetics，2015，51(3)：1-4.

[4] 李巖，李雙鵬，周吉威，等.基于定子齒削角的近極槽永磁同步電機振動噪聲削弱方法[J].電工技術學報，2015，30(6)：45-52. Li Yan，Li Shuangpeng，Zhou Jiwei，et al.Weakening approach of the vibration and noise based on the stator tooth chamfering in PMSM with similar number of poles and slots[J].Transactions of China Electrotechnical Society，2015，30(6)：45-52.

[5] 楊浩東，陳陽生，鄧志奇.永磁同步電機常用齒槽配合的電磁振動[J].電工技術學報，2011，26(9)：24-30. Yang Haodong，Chen Yangsheng，Deng Zhiqi. Electromagnetic vibration of PM synchronous motors with different combinations of slot and pole number[J].Transactions of China Electrotechnical Society，2011，26(9)：24-30.

[6] Islam R，Husain I.Analytical model for predicting noise and vibration in permanent-magnet synchronous motors[J].IEEE Transactions on Industry Applications，2010，46(6)：2346-2354.

[7] Torregrossa D，Fahimi B，Peyraut F，et al.Fast computation of electromagnetic vibrations in electrical machines via field reconstruction method and knowledge of mechanical impulse response[J].IEEE Transactions on Industrial Electronics，2012，59(2)：839-847.

[8] Dos Santos F L M，Anthonis J，Naclerio F，et al.Multiphysics NVH modeling：simulation of a switched reluctance motor for an electric vehicle[J].IEEE Transactions on Industrial Electronics，2014，61(1)：469-476.

[9] Kim D Y，Jang G H，Nam J K.Magnetically induced vibrations in an IPM motor due to distorted magnetic forces arising from flux weakening control[J].IEEE Transactions on Magnetics，2013，49(7)：3929-3932.

[10]Islam M S，Islam R，Sebastian T.Noise and vibration characteristics of permanent-magnet synchronous motors using electromagnetic and structural analyses[J].IEEE Transactions on Industry Applications，2014，50(5)：3214-3222.

[11]Chenjie L，Fahimi B.Prediction of acoustic noise in switched reluctance motor drives[J].IEEE Transactions on Energy Conversion，2014，29(1)：250-258.

[12]朱軍，田淼，付融冰，等.基于載波頻率成分的永磁同步電機轉子定位研究[J].電力系統保護與控制,2015，43(14)：48-54. Zhu Jun，Tian Miao，Fu Rongbing，et al.Research on rotor position of permanent magnet synchronous motor based on carrier frequency component[J].Power System Protection and Control，2015，43(14)：48-54.

[13]唐任遠，宋志環，于慎波，等.變頻器供電對永磁電機振動噪聲源的影響研究[J].電機與控制學報，2010，14(3)：12-17. Tang Renyuan，Song Zhihuan，Yu Shenbo，et al. Study on source of vibration and acoustic noise of permanent magnet machines by inverter[J].Electric Machines and Control，2010，14(3)：12-17.

[14]Torregrossa D，Peyraut F，Fahimi B，et al.Multiphysicsfinite-element modeling for vibration and acoustic analysis of permanent magnet synchronous machine[J].IEEE Transactions on Energy Conversion，2011，26(2)：490-500.

[15]Torregrossa D，Khoobroo A，Fahimi B.Prediction of acoustic noise and torque pulsation in PM synchronous machines with static eccentricity and partial demagnetization using field reconstruction method[J].IEEE Transactions on Industrial Electronics，2012，59(2)：934-944.

[16]Zhu Z Q，Xia Z P，Wu L J，et al. Analytical modeling and finite-element computation of radial vibration force in fractional-slot permanent-magnet brushless machines[J].IEEE Transactions on Industry Applications，2010，46(5)：1908-1918.

[17]陳湞斐，夏長亮，王慧敏.考慮齒槽效應的表貼式永磁電機空載磁場建模[J].電工技術學報，2014，29(5)：9-16. Chen Zhenfei，Xia Changliang，Wang Huimin.Modeling for open circuit magnetic field prediction in slotted surface-mounted permanent-magnet machine[J].Transactions of China Electrotechnical Society，2014，29(5)：9-16.

[18]林福，左曙光，馬琮淦，等.考慮開槽的分數槽集中繞組永磁同步電機電樞反應磁場解析計算[J].電工技術學報，2014，29(5)：29-35. Lin Fu，Zuo Shuguang，Ma Conggan，et al.Analytical calculation of armature reaction field including slotting effects in PMSM with concentrated fractional-slot winding[J].Transactions of China Electrotechnical Society，2014，29(5)：29-35.

[19]王秀和.永磁電機[M].北京：中國電力出版社，2011.

[20]Gieras J F，Lai J C，Wang C.Noise of polyphase electric motors[M].Boca Raton，FL：CRC/Taylor & Francis，2006.

(編輯 于玲玲)

Semi-Analytical Model of Vibration and Noise for Permanent Magnet Synchronous Motor Considering Current Harmonics

LinFuZuoShuguangMaoYuWuShuanglongDengWenzhe

(Clean Energy Automotive Engineering Center Tongji University Shanghai 201804 China)

This paper proposes a semi-analytical model which can be used to analyze the influence of current harmonics on vibration and noise of permanent magnet synchronous motor(PMSM)and increases calculation efficiency.Firstly，analytical method and finite element(FE)method were combined to calculate permanent magnet field and relative permeance.Analytical model for armature reaction field considering arbitrary current shape was also built and Maxwell stress tensor method was used to calculate radial force density.The result agrees well with the result that getting by FE method.Then，two dimensional(2-D)fast Fourier transform(FFT)was employed to obtain the frequency of specifically spatial order force.The stator surface vibration and noise were predicted in the case of basing on the analytical model of shell vibration and sound radiation.The predicted results were validated by tests and are able to reflect the main vibration/noise peaks and distribution.Finally，the frequency order and peak changes of vibration and noise due to current harmonics were analyzed.The work in this paper can help to analyze the vibration and noise of PMSM efficiently in the design process.

Permanent magnet synchronous motor，electromagnetic force，vibration and noise prediction，current harmonics，semi-analytical model，2-D decomposition

國家自然科學基金項目(51375343)和國家重大科學儀器設備開發專項(2012YQ150256)資助。

2016-01-22 改稿日期2016-05-03

TM341

林 福 男，1989年生，博士研究生，研究方向為永磁同步電機振動和噪聲。

E-mail：linfu_911@163.com

左曙光 男，1968年生，教授，博士生導師，研究方向為汽車動力學和振動噪聲。

E-mail：sgzuo@tongji.edu.cn(通信作者)