“三位數乘兩位數”教學研究報告

一、問題

人教版四年級上冊第三單元三位數乘兩位數是小學階段整數乘法模塊的最后一個內容。如果理解了兩位數、三位數乘一位數的乘法豎式是對加法豎式的簡寫，兩位數乘兩位數的乘法豎式記錄“用乘法分配律進行演算的算理”的一般原理，我們就不難看出三位數乘兩位數的計算與兩位數乘兩位數的計算并無本質上的區別。顯然，三位數乘兩位數的教學目標不再是掌握原理本身，而是同一原理的運用：學生能根據兩位數乘兩位數的筆算方法，類推并掌握三位數（多位數）乘兩位數的筆算方法。從這個角度看，與兩位數乘兩位數相比，三位數乘兩位數更容易被學生理解與接受，但計算難度高于兩位數乘兩位數。

（一）教學實踐中的問題

在學習三位數乘兩位數之前，為了了解學生的相關知識和經驗，保證教學活動的科學性和有效性，我們隨機抽取了三年級剛學完兩位數乘兩位數的62名學生進行了學前檢測。從前測看，大部分學生已經掌握了兩位數乘兩位數的算理。即便是沒有學過三位數乘兩位數，59.7%的學生能夠自覺遷移兩位數乘兩位數的方法，順利得出計算結果。

同時，我們對相關教師進行了問卷調查與訪談，部分老師認為學生不難獲得三位數乘兩位數的方法。但是由于計算教學的訓練單調枯燥，學生的學習熱情不高，消極應對，計算準確率低；教材中計算器的引入導致學生更加不重視三位數乘兩位數的筆算，認為大數據應該由計算器完成。此外，計算教學過分強調精確計算，忽視估算能力的培養；過分追求算法多樣化而影響了課堂教學的效率等，都是老師們在教學實踐中遇到的真問題。

（二）解決問題的策略

對于老師們在教學實踐中發現的這些問題，在進行教學設計時，我們進行了有針對性的研究，認為可以采用如下的策略進行教學實踐。

1.問題引領，促進算理正遷移。

波利亞說：“如果我們成功地回想起一個與當前問題密切相關的問題，那是很幸運的。我們應當爭取這樣的運氣。”設置“與當前問題關系密切”的問題顯然是學生順利進行正遷移的重要途徑。那么，與三位數乘兩位數非常密切的是兩位數乘兩位數。因此教師可以引導學生思考：與兩位數乘兩位數相比，今天的問題有什么不同？能不能利用兩位數乘兩位數的豎式解決？

2.任務誘發，促進算法的優化。

有人把口算、筆算、估算稱為“計算三寶”。要讓學生認識到不同的計算方法的適用性，在學習中感受到計算方法學習的樂趣，掌握運用“計算三寶”解決數學問題，教師可以精心設計問題、習題，用具體任務驅動學生的數學思考。

3.情境驅動，促進運算自動化。

運算技能的形成階段論將運算技能的形成分為認知階段———聯結階段———自動化階段，在這里也就是指小學生學習計算時經歷探索、習得計算法則的階段（如兩位數乘兩位數筆算時的程序化），到嘗試運用法則獨立進行計算的階段，再到熟練掌握并靈活運用法則的階段（如三位數乘兩位數的筆算）。心理學研究表明，當個體進入計算自動化階段以后，他們的運算速度和正確率就會大大提升。要幫助學生的運算技能實現自動化，教師可以把枯燥的計算融入到各種有趣的情境中，使學生樂在其中，在不知不覺中增加訓練，提升計算技能。

二、實踐

基于以上的思考，我們在教學三位數乘兩位數時進行了嘗試，意圖讓學生在問題的驅動下自由穿梭在各種算法中，水到渠成地達到訓練計算技能、涵養理性精神的目標。

教學過程：

1.巧設問題練口算

師：孩子們，今天這節課我們將舉行一場有趣的計算競賽。我們一起加油吧！請聽規則———在下面的7道算式中，找出能口算出得數的算式，然后算出得數，想一想你是怎樣算的。（課件出示：576×39，400×27，310×52，206×30，520×40，45×57，408×25）

生1：我覺得400×27，206×30，520×40可以口算。

（師引導學生說清算理，強調中間和末尾有0的情況，組織評價）

生2：408×25也可以口算，我知道乘25的速算規律，只要看408里面有幾個4，得數就是幾個百。

師：太厲害了，真是計算高手！

2.比較大小學估算

師：在剩下的3個算式中，不動筆計算，你能看出哪個算式的得數最大，哪個算式的得數最小嗎？為什么？

生3：得數最小的算式是45×57。因為45×57是兩位數乘兩位數，而其他的算式是三位數乘兩位數。

生4：我也認為45×57的得數最小，但是他說兩位數乘兩位數的結果一定比三位數乘兩位數的小是不對的，80×50不是比100×10大嗎？

師：你很會說理，舉例子的確是一種說理的好方法。你是怎么知道45×57的得數最小的呢？

生4：我估算出45×57大約是3000，而其他算式的得數都大于15000。

師：他采用估算的方法，真不錯！不過，老師有點好奇的是，老師還沒教三位數乘兩位數（板書課題），你怎么就會估算了？

生4：我想三位數乘兩位數的估算和兩位數乘兩位數的估算，道理是一樣的。576×39中，576大于500，39大于30，得數肯定大于15000；310×52中，310大于300，52大于50，得數也肯定大于15000。

師：真是會學習的孩子。他從兩位數乘兩位數的估算中學會了這么多道理。那么，在剩下的2個算式里，哪個的得數更大呢？

生5：576×39的得數比15000大得多，而310×52的得數更接近15000。

3.精確比較學筆算

師：576×39，310×52的得數都比15000大，如果我想知道到底大多少，怎么辦？

生：那就筆算！用計算器也可以！

師：那我們先筆算，然后用計算器檢驗，如何？（可以！）這么快就同意了，三位數乘兩位數的筆算老師還沒教呢！

生：和兩位數乘兩位數的筆算方法一樣嘛！

師：好樣的，試試吧！

學生筆算后，同桌交流算法。師指名上臺展示講解，教師及時追問并板書每一部分積的意義（如圖所示）。

師：誰還有問題嗎？

生6：310×52筆算時可不可以把末尾的0放在一邊呢？

生7：應該可以的，0乘任何數都得0，乘完0前面的數，在積的最后添上0就行了。

學生練習，指名板演（如圖所示）。

師：通過筆算，我們知道了576×29的積確實大于310×52的積。三位數乘兩位數的筆算，老師沒有教你們就會了，真棒！如果是四位數乘兩位數的筆算，你們還會嗎？如果是四位數乘三位數呢？

生8：會啊！一樣的道理嘛，只是多了一位數。

生9：四位數乘三位數，積應該有三層，第三層積的右邊第一位要和百位對齊。

師：我想，“舉一反三，觸類旁通”就是專門用來表揚你們這種孩子的！

4.靈活運用各算法

師：誰能用310×52中的5個數字編一道三位數乘兩位數的題，每個數字不能重復，積比310×52小？

學生小組活動，得到的算式有：125×30，230×15，105×23，203×15，235×10。

師：在這些算式中，哪個算式的積最小？

生10：我們認為最小數占最高位的積會比較小，125×30的積比其他算式的要大。

師：你說得有道理。剩下的算式又怎么判斷？

生11：我們認為235×10的積最小，是2350；而203×15只要把203估成200，積比3000大，明顯比2350大；105×23也比100個23多5個23，肯定比2350大；230×15的積也比3000大。

師：大家筆算105×23，檢驗你們的判斷是否正確。剛才我們玩了最小的，現在換個玩法———玩最大的。在所有三位數乘兩位數的算式中，最大的一個是多少？（999×99）不計算，你知道它的得數是幾位數嗎？為什么？

生12：這個算式的得數是五位數。因為1000×100=100000，這是一個最小的六位數，而999×99比它小，所以得數應該是個五位數。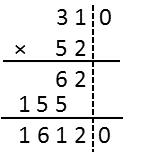

生13：我把99估成100，因為999×100=99900，實際結果比這個數要小，肯定是個五位數。

師：真是精益求精，掌聲送給計算高手！下面是四（2）班三位同學的作業，他們算得對嗎？說說理由。甲：999×99=98999；乙：999×99=99901；丙：999×99=98901。

學生觀察、思考，然后匯報。

生14：第一個算式個位上是9乘9，積的個位不可能是9，所以甲的答案肯定是錯的。

生15：第二個算式中99估成100都只有99900，積不可能大于它，所以乙的答案也不對。

生16：丙的答案不能一眼看出來，我們可以筆算。

……

師：孩子們，你們今天的表現讓老師倍感欣喜，你們的創造力遠遠超出了我的想象！

5.追根溯源釋算理

師：在很早以前，我們的祖先們是怎樣筆算乘法的呢？（課件出示：據《算法統宗》一書記載，中國明朝時期還沒有出現乘法豎式這種計算方法，古人都是用“鋪地錦”的方法計算乘法。）關于“鋪地錦”，你想了解些什么呢？請同學們看書，上面介紹的“格子乘法”就是“鋪地錦”算法。（學生閱讀）你知道怎樣用“鋪地錦”的方法計算了嗎？

學生質疑，相互答疑。

師：“鋪地錦”是古代阿拉伯人計算乘法時用的一種方法，后來傳入我國，因為計算完了以后，形如我國古代織出的鋪在地上的錦緞，人們將這種計算稱為“鋪地錦”。感興趣的孩子課后可以用“鋪地錦”的方法研究462×34。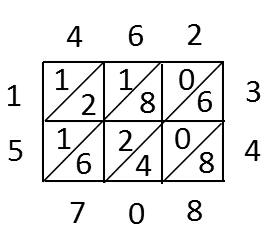

設計意圖綜述：三位數乘兩位數與兩位數乘兩位數，內容看起來差不多，但卻各有其獨特的教育功能和價值。本節課遵循因材施教理念，即因教材而教，把促進正遷移、促進計算技能形成、促進思維訓練作為主要目標，努力實現計算教學應該承載的技能習得、心智培育、習慣培養等育人價值。

1.促進正遷移。知識遷移就是人們已有的認知結構對新知識學習發生影響。本節課中，教師設計開放的問題情境，讓學生自動喚醒兩位數乘兩位數的計算經驗，自覺地建立新舊知識的關聯點，并遷移到三位數乘兩位數的學習中。因不教而會，學生自然會體驗到學習帶來的成就感。

2.促進計算技能形成。計算技能的形成離不開練習。教師需要創設高質量的問題情境，使學生能安安靜靜地思考、安安靜靜地練習。本節課中，學生在教師設計的情境中進行了口算、估算、筆算，積累了計算經驗，有利于形成扎實的計算技能。

3.促進思維訓練。對學生進行思維訓練是數學教學的重點也是難點。本節課中，教師設計的“比最小”“比最大”等教學活動都是很好的訓練數學思維的活動。學生在參與的過程中，大腦皮層始終保持最活躍的狀態，聯系、類比、假設等思維活動貫穿課堂始終，學生的心智水平也因此得以提升。

三、討論

1.學生計算水平整體下滑帶來的思考

計算教學一直是我國小學數學教學中的一個重點。新課標實施以前，大綱對學生計算能力的要求是“準確、快速、靈活、簡便”。老師們常常通過一些程式化的計算教學和大量的機械訓練使學生達到這個目標。由于這種簡單操練沒有充分實現計算教學的教育功能和培育學生素養的價值，久而久之，很多老師和孩子對計算教學活動失去了興趣，都希望能從這種機械模仿中解放出來。

隨著計算機和計算器的普及，越來越多的人認為：對學生來說，知道什么時候需要哪種計算方法，比擁有熟練的計算技能更有價值。對大數據的精算，更是可以采用現代化計算工具代勞。同時，新課標也對計算教學提出了新要求，提倡設計生動有趣的學習活動，激發學生的學習興趣，重視數學思維能力的培養。但是在實施過程中，老師們發現學生的計算水平整體下滑趨勢非常明顯，計算正確率降低、口算速度減慢現象普遍存在，學生對計算的興趣似乎也沒提高多少。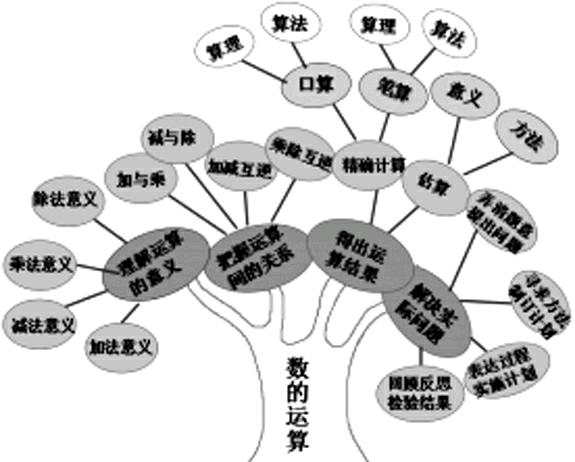

我們認為，培養學生學習數學的興趣，不能以犧牲學生的計算能力為代價，而應該對學生的計算提出清晰的要求，規范、認真、細致、準確、靈活等都是計算教學需要秉承的原則。在計算教學實施中，老師們如何正確運用教學策略，既落實計算基本功的訓練，又能最大限度地調動學生的學習積極性，發揮計算教學的育人功能，值得我們一線教師不斷思考與踐行。

2.計算教學與解決問題的聯系

數的運算一般按照理解運算的意義、把握運算間的關系、得出運算結果、解決實際問題四個部分進行教學。右圖的“知識樹”很好地概括了數的運算板塊各內容之間的結構關系。

人教版教材中將得出運算結果、解決實際問題這兩個內容結合起來教學，旨在把計算教學融入到應用中，讓學生利用問題的現實背景經歷算法的探索過程，在解決問題中認識計算的工具性作用和解決實際問題的價值。但是，我們在進行三位數乘兩位數的教學設計時，發現例1的實際問題中，學生體會不到估算的必要性。于是，我們舍棄了例1，選擇了7個簡單的乘法算式，通過問題的設計和教學情境的設置，激勵學生自主參與算理的回顧遷移、計算方法的靈活選擇與計算技能的訓練，把常見的數量關系的教學移到了下一課時。這種取舍也留給了我們一些思考：教師如何認真研討教材，做到因材施教，即準確把握什么樣的內容承載什么樣的教育功能，實現什么樣的教學目標，什么樣的教學策略能使計算教學帶來最大的效益，值得我們不斷實踐與探索。

（本文系湖南省教育科學“十二五”規劃2014年度立項課題（編號：XJK014CZXX041）研究成果）

（執筆：鄧求平、謝加文、劉碩鵬、戴益祥、王志林、王麗燕、徐旺、李闖）