固定翼二維彈道修正引信的彈簧翼改進方法

何江楊，霍鵬飛，施坤林

(機電動態控制重點實驗室，陜西 西安 710065)

固定翼二維彈道修正引信的彈簧翼改進方法

何江楊，霍鵬飛，施坤林

(機電動態控制重點實驗室，陜西 西安 710065)

針對二維彈道修正引信固定翼修正方法存在的修正能力和射程損失量對升力翼面傾角需求相矛盾問題，提出了固定翼二維彈道修正引信的彈簧翼改進方法。該方法繼承了固定翼二維彈道修正引信的設計理念，而僅將固定翼換為彈簧翼，利用迎面氣流的變化使升力翼面傾角自適應調整，在出炮口時傾角最小，而在修正段傾角最大。仿真結果表明，與固定翼修正方法相比，在修正能力相同的情況下，彈簧翼修正方法可以減小射程損失量；在射程損失量相同的情況下，彈簧翼修正方法可獲得大的修正能力。

二維彈道修正引信；固定翼；修正能力；射程損失量

0 引言

二維彈道修正引信是在傳統引信上集成二維彈道修正功能的新型引信。除具有炮彈傳統引信的起爆控制功能外，還可以同時對縱向和橫向彈道進行修正以降低落點散布，提高命中精度。因此二維彈道修正引信已經成為世界多國發展彈藥引信裝備的熱點[1]。

與導彈制導方法不同，二維彈道修正引信使用簡單、低成本的手段實現對傳統彈藥升級，短期內只用于提高對面目標的打擊精度，并不以替代導彈為目的。目前，國內外二維彈道修正引信多采用固定翼修正方法，具有代表性的為美國ATK(Alliant Techsystems Inc.，阿連特技術系統)公司PGK[2-3](Precision Guidance Kit，精確制導組件)。PGK的優點是通過對彈頭滾轉角的一維控制實現彈道的二維修正。但是它存在滿足修正能力要求的升力翼面角度帶來阻力大、射程損失大的缺點。針對二維彈道修正引信固定翼修正方法存在的修正能力和射程損失量對翼面傾角需求相矛盾問題，提出了固定翼二維彈道修正引信的彈簧翼改進方法。

1 固定翼修正方法

1.1 修正原理

二維彈道修正引信固定翼如圖1所示，其中一對為方向相反的導轉翼面，另外一對為方向相同且傾角固定的升力翼面。導轉翼面用于實現引信減旋控制，升力翼面用于產生修正力。

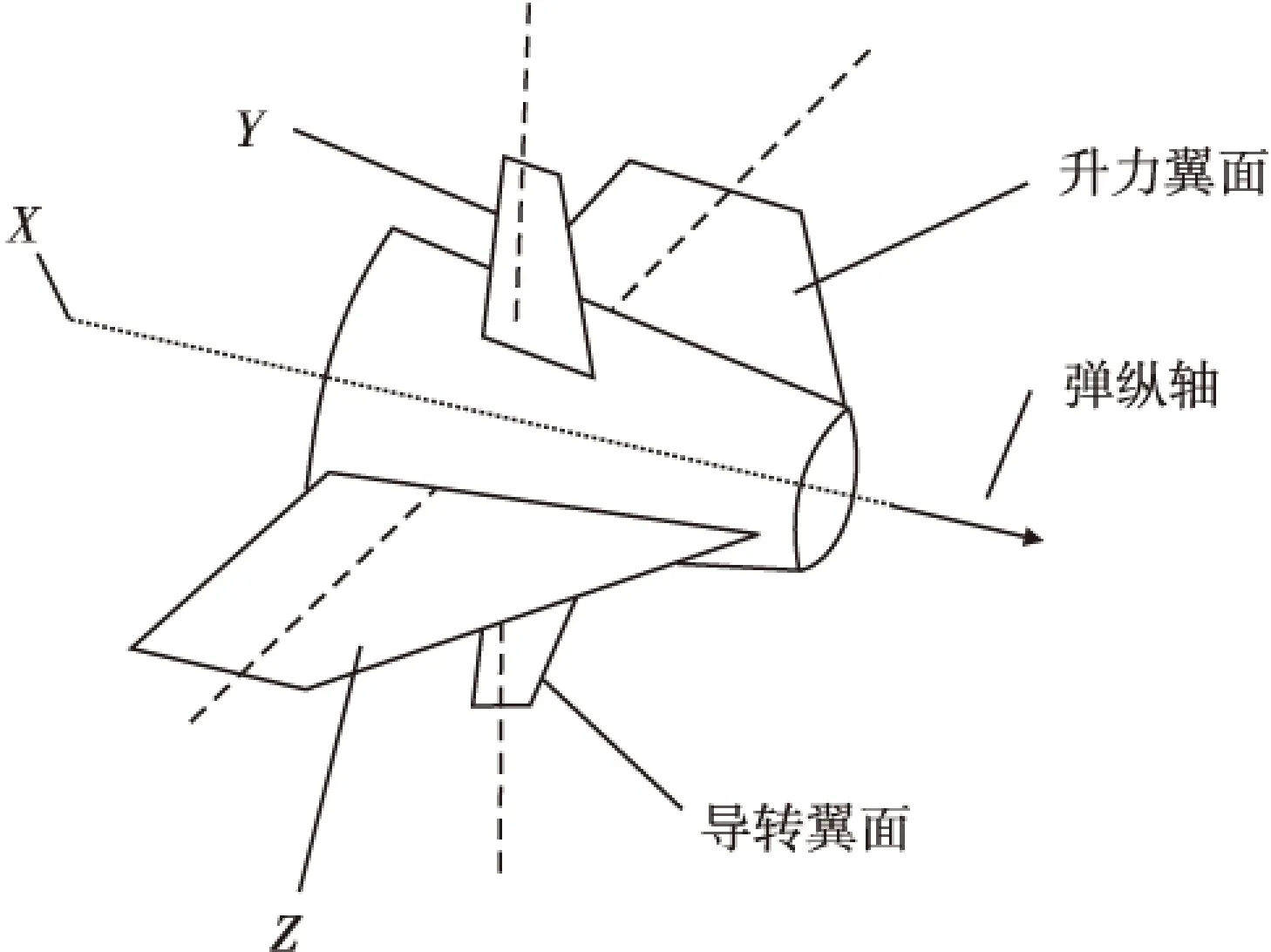
圖1 二維彈道修正引信原理示意圖Fig.1 Schematic diagram of the principle of 2-D trajectory correction fuze

通常情況下，出炮口后引信上電，進行衛星捕獲定位、引信橫滾初始對準，升力翼面在導轉翼面的作用下旋轉，平均修正力為零，在彈道初始段不進行彈道修正。待衛星定位、滾轉初始對準后，當需要進行彈道修正時，修正引信根據修正指令，通過調整導轉力矩控制引信滾轉姿態，使滾轉姿態相對大地坐標系固定在所需的滾轉角度，通過升力翼面提供特定方向的修正力，改變彈道軌跡，使彈丸飛向目標位置[4]。

1.2 升力翼面氣動力

在全彈道飛行過程中，升力翼面上作用的空氣動力會影響修正彈的修正能力和射程損失量。升力翼面受到的空氣動力可分解為沿速度方向的阻力Rx和垂直于速度方向的升力Ry。當彈軸與速度方向相同時，升力翼面阻力和升力的計算公式為[5]：

(1)

(2)

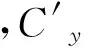
由式(1)、式(2)可知，升力翼面上作用的阻力和升力的大小與升力翼面傾角δ有關。在全彈道飛行過程中，阻力Rx的方向始終與速度方向相反，阻礙修正彈的飛行，使修正彈的射程減小。固定翼修正方法的升力翼面傾角在全彈道飛行過程中不變，滿足修正能力要求的升力翼面傾角在彈道初始不修正段時，由于修正彈速度大，空氣密度高，阻力大，會引起較大的射程損失量。而升力Ry的方向始終與速度方向垂直。在彈道初始段，引信以一定的轉速轉動，升力沿彈徑方向旋轉，由力的平均效應可得，此時修正彈不進行彈道修正；在彈道修正段，修正彈的修正能力與升力翼面傾角δ的大小有關，傾角越大，升力越大，則修正能力越強[7]。由于固定翼修正方法升力翼面傾角在全彈道飛行過程中是固定不變的，因此不能同時滿足修正能力大和射程損失量小的需求。

2 固定翼二維彈道修正引信的彈簧翼改進方法

由第1章可知，為了保證修正能力要求，升力翼面傾角必須設計得足夠大。在彈道不修正段由于修正彈彈速最高、空氣密度大，大的升力翼面傾角會引起修正彈的阻力增大，相應地，在彈道不修正段的射程損失量增大。若將傾角不可改變的固定翼改為可動翼，使升力翼面傾角在彈道不修正段盡可能小，在修正段盡可能大，從而減小修正彈在彈道不修正段射程損失量，增大彈道修正段修正能力。針對這一需求，本文提出了固定翼二維彈道修正引信的彈簧翼改進方法。所謂“彈簧翼”是指升力翼面傾角可隨著來流的不同通過彈簧彈力自適應調整而改變，在減小修正彈全彈道飛行過程中射程損失量的情況下，增大修正能力。

采用彈簧翼修正方法進行二維彈道修正，通過翼面鉸鏈力矩與彈簧力矩平衡使翼面傾角自適應調整。圖2為彈簧翼結構示意圖，其由力矩彈簧機構和靜穩定翼面組成。主要包括彈簧固定塊、彈簧、擋板、轉動桿、靜穩定升力翼面、轉軸。升力翼面與轉動桿固連，通過轉軸安裝在修正彈引信位置。由圖2可見，由于轉軸安裝在壓心的前面，來流速度大、空氣密度大時翼面傾角小，反之翼面傾角大。由此可知升力翼面傾角可實現自適應調整。

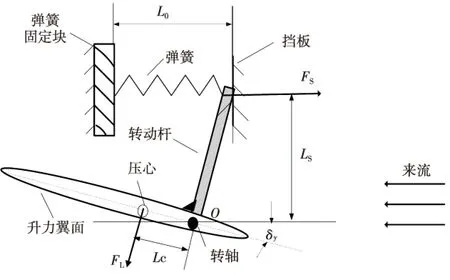
圖2 彈簧翼結構示意圖Fig.2 Schematic of the spring wing

彈簧預緊力和彈性系數多大為好，需要定量計算，可以設計這樣的彈簧：在出炮口時抗力小到使翼面傾角到達最小限位點；而在修正段抗力大到使翼面傾角到達最大限位點。

彈簧翼結構在初始狀態時，彈簧上施加有預緊力F0，彈簧處于壓縮狀態。此時，升力翼面傾角最大，為δ0。當有較大來流作用時，轉動桿離開擋板，升力翼面傾角完全由作用在升力翼面上的氣動力和彈簧彈力相對于轉軸的力矩平衡位置決定。由圖2可得，彈簧翼結構力矩平衡公式為：

FsLs=FLLc

(3)

式(3)中，Fs為彈簧由于壓縮產生的彈力，Ls為彈簧力與轉軸之間的距離，FL為作用于升力翼面的法向氣動力，Lc為升力翼面壓心與轉軸之間的距離。

彈簧上的彈力Fs計算公式為：

Fs=F0+ks(Lstanδ0-Lstanδy)

(4)

式(4)中，F0為作用在彈簧上的預緊力，ks為彈簧彈性系數，δy為彈簧翼結構的自適應傾角。

在全彈道飛行過程中作用在修正彈上的法向氣動力隨馬赫數和空氣密度變化而變化，其計算公式為：

(5)

q=ρv2/2

(6)

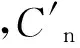
聯立公式(3)—(6)，可得

(7)

在全彈道飛行過程中，由計算精度可知，當升力翼面傾角δy≤15°時，可用(πδy/180)近似代替tanδy進行計算，則式(7)可簡化為：

(8)

由圖2和式(8)可知，當彈簧翼結構確定后，在飛行馬赫數確定情況下，升力翼面傾角由動壓q決定。在出炮口處，修正彈速度最高，空氣密度最大，使得動壓q最大。在氣動力矩作用下，轉動桿逆時針轉動，此時升力翼面傾角最小。隨著彈道升高，飛行速度降低，空氣密度變小，動壓q減小。在彈簧彈力作用下，轉動桿順時針轉動，升力翼面傾角變大。修正彈過彈道最高點后，雖然空氣密度增大，但速度衰減對動壓的影響更加顯著，因此動壓減小，升力翼面傾角繼續增大。通過以上分析可知，修正彈在出炮口后，升力翼面傾角在全彈道飛行過程中不斷增大，使得彈道不修正段的傾角比彈道修正段的小。在滿足修正能力要求的情況下，可以減小彈道不修正段的射程損失量。

彈簧翼結構需要結合不同仿真平臺的彈道特性和修正能力與射程損失量在不同彈道飛行階段對升力翼面傾角的需求，合理確定彈簧和結構的參數，滿足修正彈升力翼面傾角在不修正段小，而在進入修正段迅速增大的需求。為了滿足修正彈性能要求，需要確定彈簧預緊力的大小，由式(8)變換可得預緊力與最大升力翼面傾角之間的關系為：

(9)

由式(9)可得，要使彈簧翼結構能夠達到滿足修正能力所需要的傾角，需要對彈簧預緊力進行合理選取。在彈簧翼結構的設計過程中，通過固定翼修正方法仿真平臺確定滿足修正能力要求所需要的升力翼面傾角δ0，然后根據式(9)確定彈簧的預緊力。

3 仿真驗證

以125 mm坦克炮榴彈為算例進行二維彈道修正引信彈簧翼修正方法仿真驗證。為了仿真驗證彈簧翼修正方法的修正能力和射程損失量，選取3個典型模型，分別命名為模型1、模型2和模型3。模型1為2°固定升力翼面傾角；模型2為9.4°固定升力翼面傾角；模型3為傾角自適應調整的彈簧翼，其上施加的預緊力F0為7.5 N，彈簧彈性系數ks為500 N/m。其中，模型1和模型3射程損失量相同，模型2和模型3修正能力相同。

為了不對現有固定翼二維彈道修正引信結構布局進行大的修改，在現有固定翼二維彈道修正引信結構的基礎上，選取彈簧固定塊和擋板之間的距離L0為22.5 mm，Ls為10 mm，Lc為7 mm，假設馬赫數變化引起的翼面壓心變化可忽略不計。選取標準氣象條件，125 mm坦克炮彈的初速為850 m/s，射角為13°，在10 s開始進行彈道修正。

3.1 翼面的傾角和受力分析

建立彈道模型，對3種模型進行仿真。模型3修正彈升力翼面傾角隨時間的變化曲線如圖3所示。

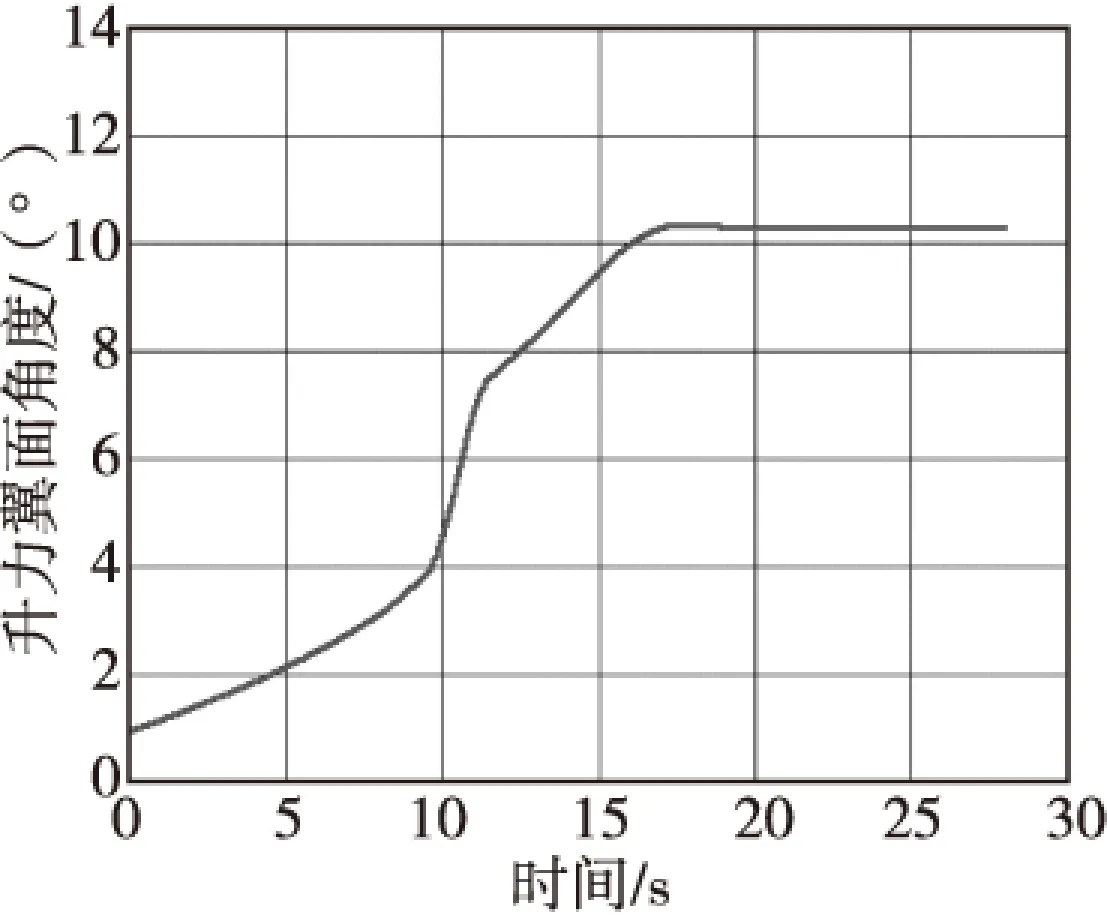
圖3 彈簧翼傾角隨時間的變化Fig.3 Variation of the spring wing angle with time

由圖3可得，模型3在第5 s前，修正彈升力翼面傾角小于2°，在15 s后，升力翼面傾角大于9.4°，在5～15 s，升力翼面傾角介于2°和9.4°之間。由此可知，彈簧翼修正方法在彈道不修正段(10 s前)的傾角較小，而在彈道修正段(10 s后)傾角增大。

在全彈道飛行過程中，對3個模型修正彈升力翼面的升力和阻力進行仿真對比，結果如圖4所示。

圖4 3個模型升力翼面受力情況隨時間的變化Fig.4 The change of the force on the wing of the 3 models with time

由圖4可知，在全彈道飛行過程中，應用彈簧翼修正方法修正彈升力翼面上作用的升力和阻力大小變化不大。在彈道不修正段，模型3和模型1修正彈升力翼面阻力值接近，但比模型2小；而在彈道修正段，模型3修正彈升力翼面升力和模型2基本一致，但與模型1相差較大，是模型1的4倍左右。由此可知，與固定翼修正方法相比，彈簧翼修正方法可以在修正段獲得較大升力的情況下，減小不修正段阻力。

3.2 修正能力和射程損失量對比

針對彈簧翼和固定翼兩種修正方法，對3種模型的修正能力和射程損失量進行仿真計算。表1所示為3種模型的修正彈射程損失量評估結果，表2所示為3種模型修正彈修正能力評估結果。由125 mm坦克炮榴彈修正能力要求可知，要求縱向修正能力為245 m，橫向修正能力為60 m。

表1 3種模型修正彈射程損失量評估Tab.1 Evaluation of 3 model for range loss of correction projectile

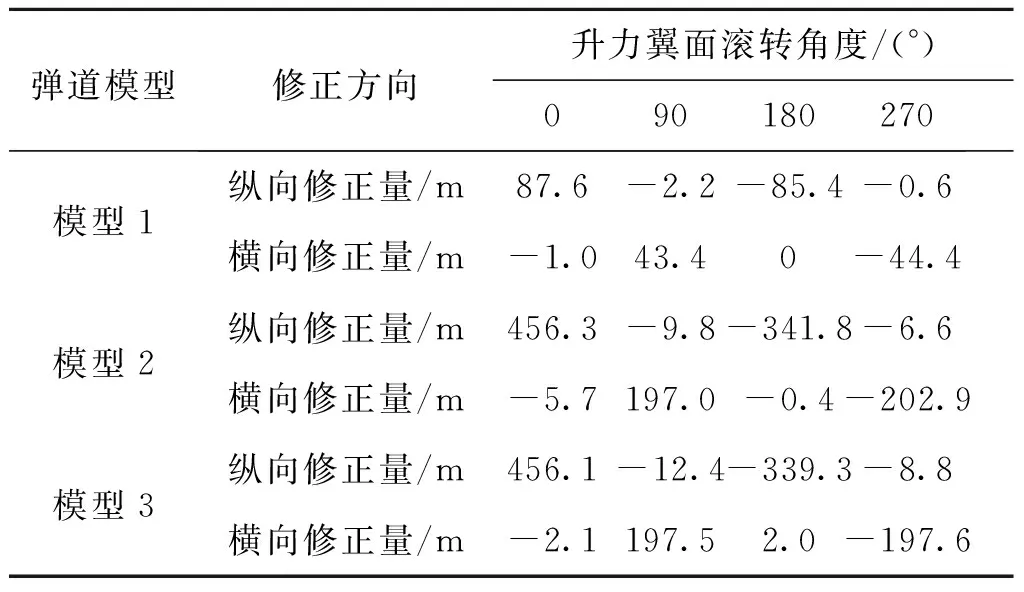
表2 3種模型修正彈修正能力評估

由表1可知，模型1和模型3射程損失量基本相同。在射程損失量相同的情況下，對兩種修正方法的修正能力進行評估。選取0°，90°，180°，270°四個引信滾轉角度對模型1和模型3的修正能力進行評估，結果如表2所示。對比模型1和模型3修正彈修正能力可以看出，模型3修正彈的修正能力遠遠大于模型1。并且由修正能力要求可知，模型3能夠滿足修正能力要求，而模型1不能滿足。由此可知，在射程損失量相同的情況下，使用彈簧翼修正方法進行二維彈道修正可以顯著提高修正彈的修正能力。

由表2可知，模型2和模型3的修正能力基本相同。在修正能力相同的情況下，對彈簧翼修正方法和固定翼修正方法的射程損失量進行評估。由表1可知，模型3比模型2射程損失量少139.1 m。由此可知，在修正能力相同的情況下，使用彈簧翼修正方法進行二維彈道修正可以減小射程損失量。

4 結論

本文提出了固定翼二維彈道修正引信的彈簧翼改進方法。該方法繼承了固定翼二維彈道修正引信的設計理念，而僅將固定翼換為彈簧翼，利用迎面氣流的變化使升力翼面傾角自適應調整，在出炮口時傾角最小，而在修正段傾角最大。仿真結果表明，與固定翼修正方法相比，在修正能力相同的情況下，彈簧翼修正方法可以減小射程損失量；在射程損失量相同的情況下，彈簧翼修正方法可獲得大的修正能力。后續需要研究滿足適配彈藥彈道特點和使用要求的彈簧翼結構參數設計優化。

[1]趙玉清,李建強,劉言,等.彈道修正引信發展綜述[J].探測與控制學報,2016,38(5)：1-5.

[2]岳松堂.國外陸軍精確制導彈藥發展分析[J].現代軍事,2015(11):56-62.

[3]美國精確制導組件技術發展現狀分析[J].四川兵工學報，2015(9):22-25.

[4]吳炎烜,范寧軍.二維彈道修正引信總體方案和關鍵技術分析[J].戰術導彈技術,2006(5)：67-70.

[5]韓子鵬.彈箭外彈道學[M].北京.北京理工大學出版社，2008:42-44.

[6]袁備,段智敏.基于固定鴨舵高速旋轉彈氣動特性[J].機電技術,2015(5):42-44.

[7]劉沖,施坤林,霍鵬飛,等.瞬態力矩平衡揭示高旋彈鴨翼對彈道的影響[J].探測與控制學報,2014,36(6):50-52.

The Fixed Wing Improvment of Two-dimensional Trajectory Correction Fuze

HE Jiangyang，HUO Pengfei，SHI Kunlin

(Science and Technology on Electromechanical Dynamic Control Laboratory，Xi’an 710065,China)

In view of the contradiction between the correction capability and the range loss of the fixed-wing of the two-dimensional correction fuze, both of which demand different angle of lift-wing, an improved method which using spring-wing instead of fixed-wing was proposed. This method inherited the design concept of the fixed-wing of the two-dimensional correction fuze, and only changed the fixed-wing to the spring-wing whose angle could be adaptive adjusted according to wind stream, which led to the smallest angle in the muzzle and the maximum in the period of correction. Simulation results showed that, compared with the fixed-wing correction method, the spring-wing correction method could reduce the loss of range under the same correction ability and obtain stronger correction ability under the condition of the same range loss.

two-dimensional trajectory correction fuze; fixed-wing; correction ability; the loss of range

2016-11-09

何江楊(1991— )，男，陜西米脂人，碩士研究生，研究方向：彈道修正引信。E-mail:714409370@qq.com。

TJ43

A

1008-1194(2017)02-0034-04