基于HJC模型的鋼筋混凝土侵徹仿真失效準則與參數

林 琛，徐建軍，楊晉偉，張海良

(1.中北大學機電工程學院，山西 太原 030051；2.淮海工業集團有限公司，山西 長治046000)

基于HJC模型的鋼筋混凝土侵徹仿真失效準則與參數

林 琛1，徐建軍1，楊晉偉2，張海良2

(1.中北大學機電工程學院，山西 太原 030051；2.淮海工業集團有限公司，山西 長治046000)

針對侵徹鋼筋混凝土各種本構模型失效定義不夠完善的問題，提出了基于HJC材料模型的鋼筋混凝土侵徹仿真失效準則與參數的方法。該方法是基于HJC本構模型自帶的失效準則定義，運用LSDYNA算法修正HJC材料模型中的失效控制參數FS，采用上述模型自帶的失效準則與參數并聯合其他三種輔助失效準則來彌補HJC材料模型在失效定義方面的不足。侵徹試驗結果表明，該數值模擬方法產生的侵徹貫穿現象與試驗結果基本相同，因此該數值模擬方法具有一定的工程價值。

HJC材料模型；侵徹；鋼筋混凝土；數值模擬；單元失效準則

0 引言

鋼筋混凝土的侵徹和貫穿問題涉及到彈靶的幾何尺寸與結構、材料強度、應力波的傳播、摩擦效應等諸多因素[1-2]。由于通過理論分析去獲取解析解有相當程度的復雜性而實際靶場試驗的成本高昂，且打靶測試的數據適用范圍較窄，故而針對此類問題目前廣泛運用數值模擬的方法。

數值模擬結果的準確性與鋼筋混凝土的建模方法、混凝土材料動態本構模型及失效準則與參數等因素密切相關[3]。由于鋼筋作為傳統金屬材料，其本構關系與損傷較為明確。近年來國內外對于數值模擬侵徹鋼筋混凝土的失效準則與參數問題研究主要集中在混凝土材料動態本構模型關于失效的定義。文獻[4]提出了TCK模型；文獻[5]提出了RHT模型；文獻[6]提出了HJC模型；文獻[7]考慮了洛德角的影響得到改進MHJC模型；而馬愛娥等[8]以TCK模型和HJC模型為基礎,自定義了混合型損傷模型作為混凝土的本構模型。

雖然隨著混凝土材料的動態本構模型不斷改進，失效的定義得到不斷的發展。但是由于鋼筋混凝土在侵徹加載條件下的損傷具有高度的復雜性。上述各種本構模型失效定義仍無法模擬侵徹混凝土材料的全部失效形式。尤其是侵徹鋼筋混凝土材料時需要特別考慮混凝土的骨料、孔洞等在結構中的隨機性分布而造成對鋼筋材料在沖擊載荷作用下變形破壞。在這一方面HJC材料本構模型考慮得較為全面。

LSDYNA中的關鍵字*MAT_ADD_ERROSION提供了8種輔助單元失效準則，加上HJC模型中自帶的失效準則與參數。故而HJC模型有更為豐富的失效準則可供選擇。對于完善侵徹作用下鋼筋混凝土關于失效的定義，究竟采用哪種輔助失效準則最為合適，目前沒有定論。文獻[9-10]采用最大靜水壓和最大剪應變失效準則綜合控制, 模擬的結果在漏斗坑形成方面不明顯。而文獻[11-12]分別采用單一失效準則控制，其侵徹工況與現實試驗工況偏差太遠。且綜合國內外已有的眾多相關研究中鮮有關于其最后一個關鍵字參數FS的理論性的研究。

本文針對上述侵徹鋼筋混凝土各種本構模型失效定義不夠完善的問題，提出了基于HJC材料模型的鋼筋混凝土侵徹仿真失效準則與參數的方法。

1 HJC本構模型

HJC材料模型,是由金屬材料中廣泛應用的JC(Johnson_Cook)模型發展而來，其特點是能夠反映混凝土等脆性材料在大應變、高應變速率和高圍壓下及材料損傷失效的動態響應。

HJC本構模型主要包括三方面:狀態方程、屈服面方程以及損傷演化方程,下面分別對各部分作簡要介紹和分析。

1.1 狀態方程

材料所受壓力P與相應的應變μ的關系曲線如圖1所示。

圖1 HJC材料狀態方程Fig.1 State equation of HJC

1.1.1 拉伸狀態方程

1)線彈性階段

P=Kμ

(1)

2)裂縫貫通斷裂階段

P=T(1-D)

(2)

式(2)中，T是材料最大拉伸截止靜水壓力，D是材料的損傷程度。

從圖1可知即使此時拉應力不再變化然而應變卻依舊緩慢增大，即可以看出該本構模型在拉伸失效描述與現實混凝土拉伸失效相比過于簡單。

1.1.2 壓縮狀態方程

在該材料本構模型的壓縮階段又分為：線彈性階段、過渡階段和壓實階段。

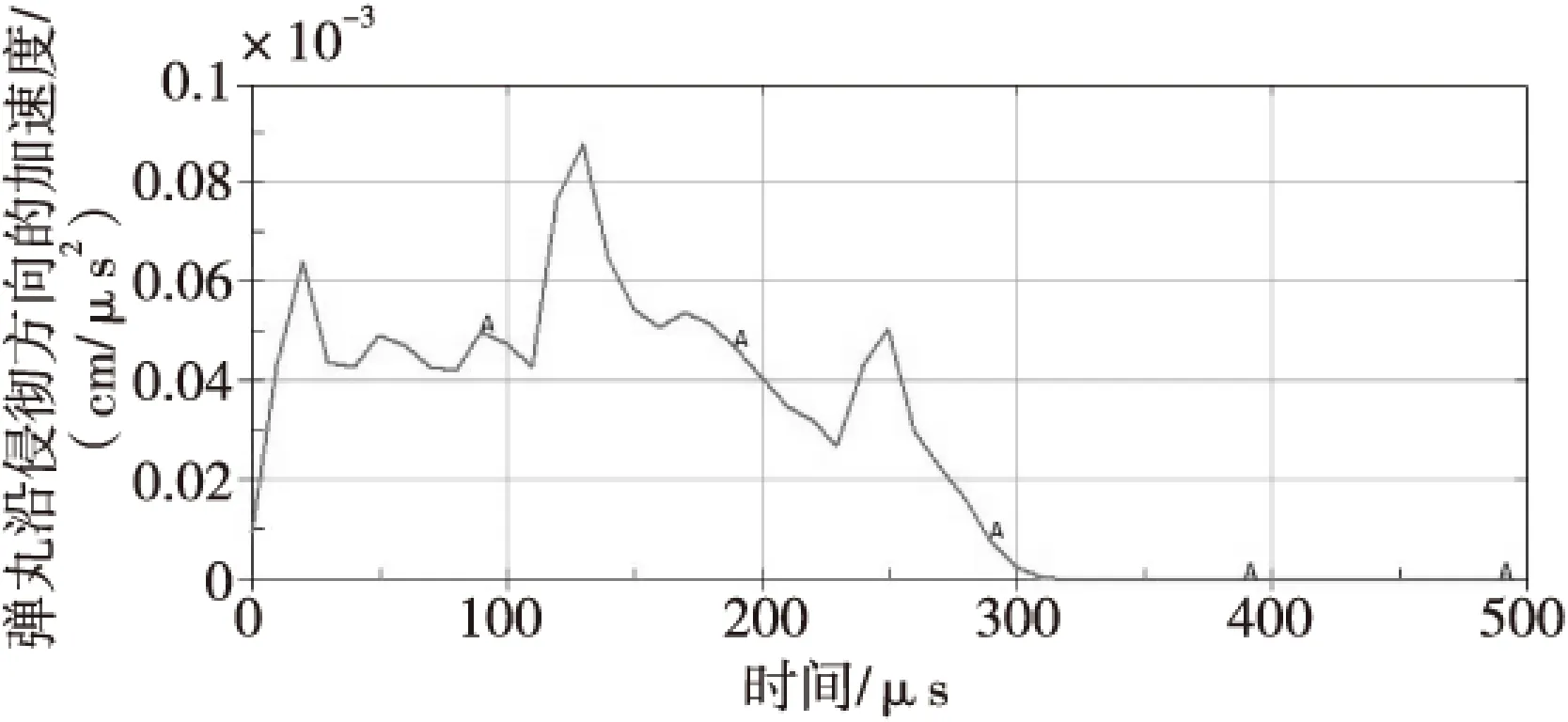
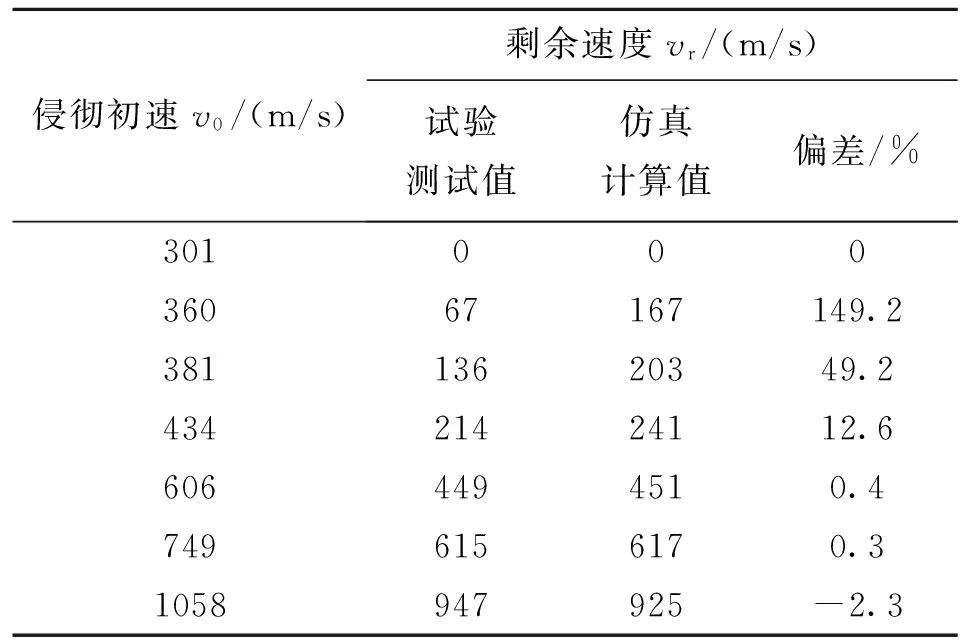
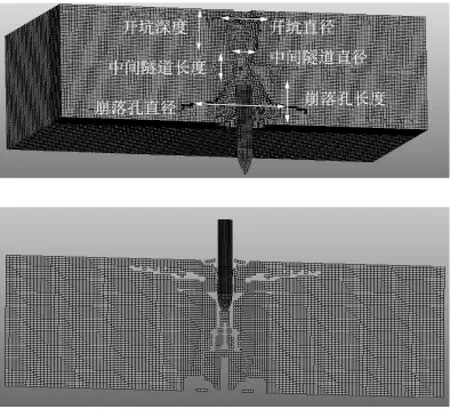
1)線彈性階段(0

2)過渡階段(Pcrush≤P≤Plock)時，這一階段是指混凝土內部的氣泡開始破裂，混凝土結構受到損傷，并開始產生破碎性裂紋，但混凝土結構還沒有完全破碎。

P=Pcrush+Kcrush(μ-μcrush)

(3)

式(3)中，Kcrush=(Plock-Pcrush)/(μlock-μcrush)，Plock為材料空隙全部閉合時的臨界壓力，μlock為對應的體積應變。

3)壓實階段(P>Plock)時，當壓力達到Plock,混凝土內部氣孔被完全壓碎。關系式常用三次多項式表示：

(4)

1.2 屈服面方程

HJC模型的屈服面可表述為：

(5)

1.3 損傷演化方程

HJC損傷模型如圖2所示。模型損傷由塑性應變累積而成，其中塑性應變包括了等效塑性應變和塑性體積應變。其損傷演化方程為：

(6)

(7)

(8)

式中，ΔεP和ΔμP分別為當前積分步下的等效塑形應變增量和塑性體積應變增量，P是實際的壓力,EFMIN是材料最小破碎應變，T*=T/fc為無量綱最大靜水壓力。f(P)為常壓P作用下材料發生斷裂時的塑性應變。

圖2 HJC材料損傷模型Fig.2 Damage model of HJC

2 單元失效準則與參數

2.1HJC自帶失效準則與參數(FS)分析

HJC材料模型材料單元破壞的雙門開關是等效塑性應變ε和損傷度D。而手冊中HJC材料模型關鍵字文件里提到“FS>0時，當單元的有效塑性應變>FS失效”[12]。基于此可以很初步推得如下假設：FS是HJC材料模型在壓力P作用下材料發生斷裂與否的塑形應變的閾值。即可用下式表示為：

FS=f(P)max=D1(Pmax*+T*)D2

(9)

結合式(7)和式(9)得到FS實際的意義如下：1)當設定FS>0時，表示選擇了材料受壓失效模式，FS的值是材料等效塑性應變失效控制的下限閾值；2)當設定FS=0時，由式(9)可知P*+T*=0即P*=-T*，即壓力為無量綱最大靜水壓力的負值(實際為拉應力)，表示材料選擇了拉伸損傷失效模式，FS的值是無量綱靜水拉力的閾值，當拉應力-P*>T*材料失效；3)當設定FS<0時，結合式(7)和式(9)可得D<0表示材料選擇了損傷程度D控制失效模式，當材料累積損傷程度D<0時材料宣告失效。

由上述該材料的本構模型可以看出P隨體應變μ的增大而增大，而混凝土材料模型在壓實階段存在一個壓實密度ρcom，當混凝土介質受到高速高壓沖擊時其密度會迅速地由初始密度ρ0達到壓實密度ρcom，進入壓實密度以后材料繼續受壓其密度變化十分微小，從而可以合理假設：當材料受壓的壓力成倍地增長而相應的密度變化卻小于1%時，可認為混凝土材料已經達到其極限密度ρmax，即：ρmax=(1+0.01)ρcom。相應此時的體應變達到最大值μmax，混凝土承受最大靜水壓Pmax。而從文獻中可以查閱到壓實密度的數據ρcom=2.68 g/cm3。

從而由上述假設可以得到材料的壓縮極限密度ρmax，結合壓實階段狀態方程(4)以求出μmax和Pmax。并將求出的Pmax帶入式(9)，從而可以量化計算出FS的數值為1.3。

2.2LSDYNA提供的多種單元失效準則

LSDYNA通過關鍵字*MAT_ADD_ERROSION提供了多種輔助單元失效準則。常用的失效準則有：最大靜水拉(壓)應力失效準則(拉為正，壓為負)、最大主應力失效準則、最大等效應力失效準則、最大主應變失效準則、最大剪應變失效準則、等效塑性應變失效準則等。

2.3 侵徹鋼筋混凝土目標的失效準則的選擇

一方面由于侵徹鋼筋混凝土目標涉及到靶板正面開坑、貫穿孔徑、漏斗坑以及靶板背面的層裂與崩落現象。其中用最大單元剪應變失效準則控制可以有效地模擬出靶板的正面開坑現象；且單就HJC材料本構模型而言，該本構模型在模擬混凝土的壓縮失效方面具有較為理想的效果(剩余速度和侵徹深度方面)，故而采用HJC自帶失效準則的壓縮失效模式(控制參數FS=1.3)并聯合剪應變失效準則共同控制單元壓縮失效。

另一方面由于HJC本構模型在拉伸失效方面的描述不足，無法模擬出侵徹混凝土目標時的靶背崩落、層裂以及漏斗坑現象，故而還需要添加最大靜水拉應力失效準則與最大拉伸主應力失效準則共同模擬鋼筋混凝土材料受到侵徹時所受的拉伸失效。

3 數值模擬與試驗的對比驗證

參考S.J.Hanchak等試驗的動能彈侵徹鋼筋混凝土所用的彈靶尺寸。用分離式方法建立鋼筋混凝土靶板的有限元模型，并采用上述方法所確定的單元失效準則與參數，對彈丸侵徹鋼筋混凝土靶板的動態響應過程進行數值模擬。關注點側重于數值模擬獲取的侵徹過載信號與侵徹靶板的貫穿孔通道以及鋼筋網絡破壞情況和整體靶板的破壞工況。

3.1 剩余速度與減加速度分析

在數值模擬中同樣采用靶場試驗所用的相同的一系列彈丸入射速度來模擬，并將數值模擬結果所得的剩余速度與靶場試驗所得的數據進行比對。以各種不同入射速度侵徹的數值模擬剩余速度結果如圖3所示。

而關于侵徹過載的另外一個重要信號：彈丸減加速度信號，圖4中清晰地表現了彈丸侵徹靶板時三層鋼筋網對于彈丸速度的擾動影響，并且由此可以合理的推論出高配筋率的鋼筋網對于防護侵徹能有極為正面的作用[13]。

圖3 各種不同初速侵徹時彈體速度變化曲線Fig.3 Chart of projectile’s velocity in various initial velocities’ penetration projectile’s

圖4 749 m/s初速侵徹的加速度過載曲線Fig.4 Chart of acceleration in duration of penetration by 749 m/s impact

最后進一步將數值模擬的剩余速度與前人若干侵徹試驗所測得的剩余速度做更為直觀的統計，如表1所示。

表1 剩余速度統計對比表

從表1可以看出，該數值模擬方法在侵徹初速大于600m/s以上時誤差較小，獲得的侵徹過載信號在速度和加速度方面都與試驗數據接近，偏差不大。

侵徹過程中彈尖對周圍的靶體材料產生擠壓,當擠壓過程產生的側向應力大于靶體材料的抗剪強度(剪切失效應變控制)時，靶體材料就產生了剝落，應力越大，產生的剝落塊就越大，即正面開坑。本文單就剪切失效應變閾值而言設置略微偏大，導致在靶體側向損耗彈丸動能方面模擬略為不足，尤為明顯地表現在當著靶速度低于600m/s時，側向應力不足以讓剪切失效發揮作用，開坑剝落比實際小許多，從而彈丸動能損耗偏小，影響的結果是剩余速度失真且數值偏大。因本文是驗證不同著靶速度以相同的失效準則與參數控制下的侵徹結果，所以沒有按照著靶速度等不同初始條件去調整失效準則的控制參數，且統一對照組里如果將剪切失效閾值調低，中高速侵徹剩余速度會失真，偏小。現實模擬時，可按照侵徹初始條件不同相應地去合理調整失效準則的控制參數以達到理想的模擬結果。

3.2 混凝土靶板貫穿破壞工況分析

圖5和圖6分別為彈體以749m/s初速侵徹鋼筋混凝土時靶板的正面和背面損傷圖。可以看出正面靶板的破壞損傷主要顯現的是壓縮破壞損傷，由靶板侵徹通道的開坑口向靶板邊緣有相對較長的徑向裂紋，且在開坑口附近有環形的小裂紋。從數值模擬與試驗實際情形的對比圖可以看出，靶板的正面開坑破壞情形除了開坑略淺，其他與試驗結果比較吻合。而靶板背面破壞區域有較長較大的徑向裂紋和環向裂紋，拉伸破壞現象較為明顯。

圖5 靶板正面損傷試驗與數值模擬情況的對比Fig.5 Damage of target’s front face compare between experiment and simulation

圖6 靶板背面損傷與數值模擬情況的對比Fig.6 Damage of target’s back face compare between experiment and simulation

自由面反射形成的拉伸波在靶板內形成裂紋并擴散從而導致了層裂現象出現，彈體在侵徹過程中在靶板的正面和背面都產生了一個圓錐體的漏斗形的彈坑。與Hanchak等人的試驗進行比對，并從數值模擬的侵徹貫穿通道情況圖7和圖8可以看出，數值模擬的結果與試驗結果情形吻合得較為良好。而靶板背面的崩落現象產生的原因是由于自由面附近應力的疊加合成產生拉伸損傷[14]，如圖8所示。

從圖7和圖8可以看出，本文采取的失效控制參數能有效地模擬出開坑、層裂、崩落、漏斗坑等侵徹混凝土目標時產生的各類靶板破壞形態。隨著彈體速度的增大，侵徹開坑直徑、中間隧道的直徑、崩落孔的直徑和崩落的長度也隨之增大，而中間隧道的長度隨之略微減小。其中單就749m/s初速侵徹工況來看，其數值模擬的工況為：侵徹開坑直徑約為彈體直徑的2倍(而試驗約為2～2.5倍)，崩落孔直徑約為彈體的4.5倍大小(試驗的大小約為5倍)，中間隧道長度與靶板前后面的漏斗形坑長度近乎各占1/3，這也與文獻[15]所述相符。

圖7 360 m/s和434 m/s初速侵徹條件下數值模擬的侵徹貫穿通道情況Fig.7 Simulation of 360 m/s and 434 m/s impact target’s penetration path

圖8 數值模擬749 m/s初速的侵徹貫穿通道與崩落的剖面示意Fig.8 Simulation of 749 m/s impact target’s penetration path and its collapse

3.3 鋼筋網變形與破壞工況分析

圖9 三層鋼筋網的破壞與變形情況Fig.9 Destruction and deformation condition of 3 layers reinforced steel

彈丸侵徹鋼筋混凝土靶板時，彈丸侵徹完靶板正面保護層水泥撞擊到第一層鋼筋網，彈丸撞擊靶板使得靶板在徑向受到沖擊壓力，進而使得鋼筋網眼的變形在鋪層面上沿徑向變化。具體變形情況和破壞情況從上面兩圖可以看出：第一層鋼筋網的撓度變形與侵徹沖擊的方向相反；而第二層鋼筋網的變形破壞僅有些微的層面外脹；第三層鋼筋網的撓度變形則與侵徹沖擊方向相同。同等直徑大小的鋼筋，彈丸的速度或者質量越大，鋼筋變形越大，破壞越顯著。類似的計算現象在文獻[15]中也曾出現并被提及過。

4 結論

本文提出了基于HJC材料模型的鋼筋混凝土侵徹仿真失效準則與參數的方法，該方法是基于HJC材料模型自帶的失效準則定義，運用LSDYNA算法修正HJC材料模型中的失效控制參數FS，采用上述模型自帶的失效準則與參數并聯合其他三種輔助失效準則來彌補HJC材料模型在失效定義方面的不足。實際侵徹試驗結果表明，該數值模擬方法產生的侵徹貫穿現象與試驗結果基本相同，因此該數值模擬方法具有一定的工程價值。

[1]聶明飛，李玉龍.卵形頭部彈侵徹單多層混凝土靶板有限元仿真[J].探測與控制學報，2009，31(4)：78-83.

[2]周寧，任輝啟，沈兆武，等.侵徹鋼筋混凝土過程中彈丸過載特性的實驗研究[J].實驗力學，2006，21(5)：572-578.

[3]李猛深,李宏,馮淑芳.彈體侵徹鋼筋混凝土的數值計算方法研究綜述[C]//第四屆全國工程安全與防護學術會議論文集.洛陽：中國巖石力學與工程學會，2014: 659-662.

[4]TaylorLM,ChenEP,KuszmaulJS.Micro-crackinduceddamageaccumulationinbrittlerockunderdynamicloading[J].ComputerMethodsinAppliedMechanicsandEngineering,1986，55:301-320

[5]RiedelW,ThomaK,HiermaierS,etal.PenetrationofreinforcedconcretebyBETA2B2500numericalanalysisusinganewmacroscopicconcretemodelforhydrocodes[C]//9thInternationalSymposium,InteractionoftheEffectsofMunitionswithStructures.Berlin-Strausherg:I13MAC,1999:315-322.

[6]HolmquistTJ,JohnsonGR.Acomputationalconstitutivemodelforconcretesubjectedtolargestrains,highstrainratesandhighpressures[C]// 14thInternationalSymposiumonBallistics，Canada，1993:591-600.

[7]JavierLMalvar,CrawfordJohnE，WesevichJamesW，etal．AplasticityconcretematerialmodelforDYNA3D[J]．InternationalJournalofImpactEngineering，1997，19(9)：847-873.

[8]馬愛娥，黃風雷，李金柱，等.鋼筋混凝土抗貫穿數值模擬[J].北京理工大學學報，2007,27(2)：103-107.

[9]王建剛.子彈侵徹鋼筋混凝土的數值模擬研宄[D].北京：國防科學技術大學，2011.

[10] 胡懷春.侵徹混凝土目標貫穿特性分析及靶后炸點精度控制研究[D].南京：南京理工大學，2014.

[11]林華令，丁育青，文輝.混凝土侵徹數值模擬的影響因素[J].爆炸與沖擊，2013,33(4)：425-429.

[12]姜華，王君杰.彈體侵徹混凝土數值模擬失效指標[J].振動與沖擊，2009,28(8)：30-34.

[13]LS-DYNAkeywordsusre'smanual(version971/Rev5)[M].California:LivermoreSofewareTechnologyCorporation，2010.

[13]樓建鋒，王政，朱建士，等.含筋率和彈著點對鋼筋混凝土抗侵徹性能的影響[J].爆炸與沖擊, 2010, 30(2): 178-182.

[14]武海軍, 黃鳳雷 ，金乾坤，等.彈體貫穿鋼筋混凝土數值模擬[J].爆炸與沖擊, 2003, 23(6): 545-550.

[15]龐洪鑫.高速侵徹鋼筋混凝土靶板的數值模擬研究[D].北京：北京理工大學，2015.

The Failure Criterions and Parameters of HJC Model Based Perforation Simulation

LIN Chen1，XU Jianjun1, YANG Jinwei2,ZHANG Hailiang2

( 1. College of Mechanic and Electronic Engineering,North University of China,Taiyuan 030051,China; 2. HuaiHai Industrial Group.,Ltd, Changzhi 046000,China )

Aiming at the inadequate descriptions in definitions of elements’ failure for the various constitutive models of reinforced concrete, a new approach by rectifying the parameter FS of HJC material model ,base on LSDYNA’s algorithms was presented. By adopting the combinations of criterions of element’s failure, which was offered by FS and LSDYNA, the numerical simulation of projectile’s penetration into reinforced concrete was carried out. It was proved that this method had a certain value in engineering by contrasting with the counterpart practical experiments.

HJC; perforation; reinforced concrete; numerical simulation; failure criterions

2016-10-22

林琛(1989—)，男，江西上饒人，碩士研究生，研究方向：機電控制系統。E-mail:814035759@qq.com。

TJ430.6;TM89

A

1008-1194(2017)02-0100-06