基于模糊聚類及馬爾科夫殘差修正的び沒Р嘍唐詬漢稍げ夥椒

賈永奎 李大凱 許鵬

摘要：針對用戶側短期負荷隨機性強、環境敏感度高的特點，提出了一種基于模糊聚類的馬爾科夫用戶側短期負荷預測方法。采用模糊聚類方法對用戶歷史負荷數據進行可定義顆粒度的預處理，并以負荷所映射指標集構建的聚類識別指標為依據，通過指標隸屬和距離校驗對當前用戶負荷模式準確歸類；進而在所屬類中心基礎上進行馬爾科夫殘差預測。最后實驗表明該方法能良好適應用戶負荷特性，有效提高預測精度。

關鍵詞：短期負荷預測；模糊聚類；馬爾科夫；殘差預測修正

隨著電力調度及能源管理技術的發展，短期甚至超短期負荷預測越來越體現出其重要性[1]。已有的電力負荷預測主要面向省網或區域電網級的整體負荷特性[2]。而電力微網及分布式能源技術的發展使得電力管理已逐步向更加信息化、互動化和精細化的管理模式轉變；電力大數據時代的到來也對用電負荷預測和用電行為分析提出更高的要求，面向用戶的短期甚至超短期用電負荷預測關系到電力的未來發展[3]。短期負荷預測多樣性較強，負荷特性受溫度、氣候及日期類型等因素的影響相對較大，且不同用戶群體對各因素的敏感度也具有一定的差異性[4]。

基于上述考慮，本文提出一種基于模糊聚類的用戶側短期負荷馬爾科夫預測方法，實現考慮多影響因素的聚合情況下，通過預測方法進行進一步修正和精確化。

1 基于模糊聚類及馬爾科夫的負荷預測

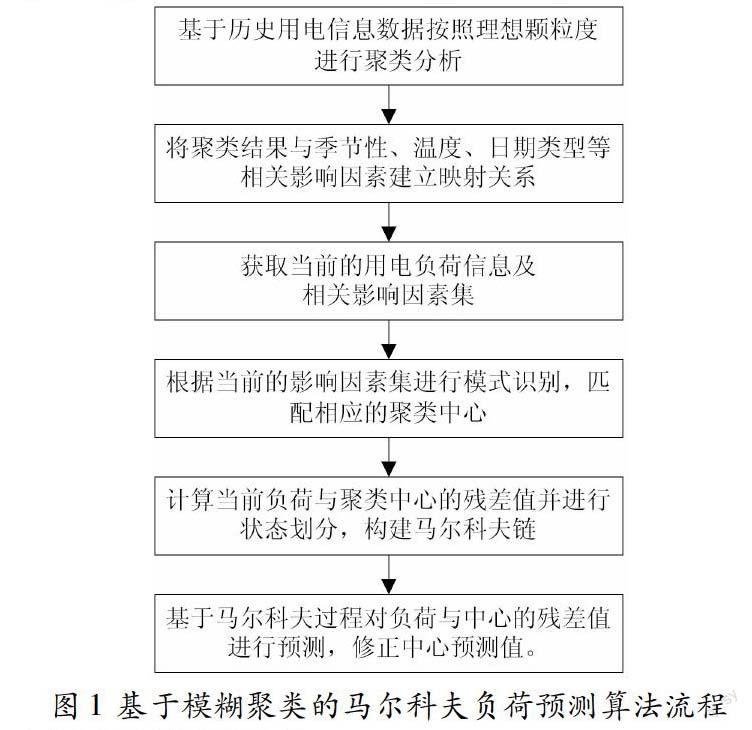
本文對用戶側短期用電負荷的預測方法總體流程構架如圖1所示：首先基于歷史用電信息數據進行聚類分析，按照理想顆粒度對用戶側的用電負荷模式進行類別劃分，得到若干種用電模式；其次將聚類結果與相關影響因素之間建立映射關系；然后匹配相應的聚類中心；最后對當前負荷與聚類中心的殘差值進行狀態區間劃分并以馬爾科夫預測方法對殘差值進行預測，從而實現從聚類中心到實際負荷間的進一步修正。

2 歷史數據聚類分析

本文對于歷史數據的分析采用C均值模糊聚類方法，對用戶的歷史日負荷數據進行聚類分析。

設樣本數據集為用戶在n天中的負荷數據，其中ui=[ui1，ui2，...，ui24]T表示每天的負荷數據向量；設樣本指標集V=[v1，v2，...，vn]T與數據集間一一映射，其中：

vi=[vdtype，vweather，vhtmp，vltmp，vhumi，vwind]T

其中vdtype，vweather，vhtmp，vltmp，vhumi，vwind分別表征當前的日期類型、天氣、最高溫度、最低溫度、濕度、風級等與負荷特性相關的影響因素向量。

則對數據集進行模糊聚類的過程可表達為：初始化聚類中心矩陣λ（0）為若干典型指標集所對應的負荷數據，如式1所示：

根據式2可在D基礎上求得樣本數據的劃分矩陣QC×n，并根據式3更新聚類中心λ直至劃分矩陣穩定不變。則所得隸屬度聚類中心λ即可作為將來負荷預測的依據。

3 馬爾科夫鏈殘差序列預測

負荷的模糊聚類結果中心僅根據歷史數據求得，與用戶當前的負荷情況必然存在一定的偏差，為縮小這一偏差，本文通過馬爾科夫過程對其殘差序列進行預測。馬爾科夫預測一般要求滿足穩定性假設[5]，考慮到用電負荷與時間點關聯較大，并不滿足這一條件，而結合已有的用戶運行模式判定，以聚類中心為基準的負荷數據波動和時間點并不具有明確的關系，更滿足于穩定性假設。因此本文算法設計中對負荷數據與聚類中心間的殘差序列進行馬爾科夫預測修正。

基于上述分析，采用目標時刻用電數據與聚類中心對應數據的差值作為殘差，根據式（4）計算用戶當前時刻及前若干時間點的殘差序列；根據式（56）將殘差序列采用均值標準差分級方法劃分為5個不同的狀態區間{S1，S2，S3，S4，S5}；根據一定時期內的歷史統計數據根據式（7）馬爾科夫狀態空間轉移概率，構建一步概率轉移矩陣P。

4 實驗分析

本文中以某電力用戶2014年2月6日～2月16日的用電負荷數據為依據，進行實驗仿真分析，并采用自回歸滑動平均模型（ARMA）和灰度預測模型（GM）進行預測作為對比，結果對比如圖2。

可見，GM預測方法的曲線明顯波動較小，相對較為平滑，這是由于GM預測方法對數據的平滑性要求較高，適用于相對波動較小的預測對象，如針對整個地區電網范圍的負荷預測；而由于ARMA預測對數據的平穩性有一定要求，對于短期波動較大的情況其精度會受到影響，因此其預測結果體現出偏離實際曲線的波動性；相對而言，較為精細和準確的聚類結果與實際負荷整體上是比較貼近的，只在部分突變點出現較大偏差，而本文的預測結果中，在聚類中心的基礎上體現了較強的矯正作用，預測值整體上比聚類中心更貼近實際。可見本文算法能相對較好地適應用戶負荷的不確定性，更準確地反映負荷走向。

根據上述實驗結果，本文算法能相對較好地適應面向用戶的負荷強波動性以及短期負荷的隨機性，較為精確地對面向用戶的短時用電負荷進行預測，為面向智能配用電的用戶用電負荷分析提供了可靠的基礎，尤其對于智能配用電大數據處理分析具有較強的實際意義。

5 結語

本文中的算法提出在考慮負荷影響因素及歷史負荷情況的前提下，通過預測方法進行有效改進和修正。模糊聚類使得算法的擴展性和應用性更強，更易于適應不同用戶對影響因素的敏感性差異；而通過指標集和中心距離雙標準的負荷模式判別則保證了判定的準確性，減小指標集意外的突發情況影響。而馬爾科夫殘差預測修正則是對這一結果的進一步精確化，實驗結果顯示算法能有效提升預測精度。

參考文獻：

[1]焦潤海，蘇辰雋，林碧英，等.基于氣象信息因素修正的灰色短期負荷預測模型[J].電網技術，2013，37（3）：720725.

[2]劉旭，羅滇生，姚建剛，等.基于負荷分解和實時氣象因素的短期負荷預測[J].電網技術，2009，33（12）：94100.

[3]張春雷.基于模糊聚類和粗糙集的電力系統短期負荷預測[J].華北電力大學學報（自然科學版），2008，03：3843.

[4]于龍.基于模糊聚類選取相似日的短期電力負荷預測[D].上海交通大學，2013.

[5]黃銀華，彭建春，李常春，等.馬爾科夫理論在中長期負荷預測中的應用[J].電力系統及其自動化學報，2011，05：131136.