On the Hadamard-like inequality

WANG Juping, GUO Dongxing, CAO Hongyan, WANG Shuling, ZHANG Chichen

(Shanxi Medical University, Department of Mathematics, Taiyuan 030001)

On the Hadamard-like inequality

WANG Juping, GUO Dongxing, CAO Hongyan, WANG Shuling, ZHANG Chichen*

(Shanxi Medical University, Department of Mathematics, Taiyuan 030001)

In this paper, a problem called Hadamard-like inequality proposed by Minghua Lin is partially proved. It is directly proved that it holds forn=4 and fails forn=2,3. For a special case of tri-diagonal matrices it is proved to hold for anyn≥3. Finally, a new Hadamard-like inequality that holds for all Hermitian matrices of ordern(?n≥2) is generated.

determinant； Hadamard-like inequality； Hermitian matrices

1Introduction

As the cornerstone of algebra and the important tool of other disciplines， the determinant looks like a magic cube which presents lots of difficult mathematical problems. It also greatly enriches the theory of algebra. In the history of mathematics， many scholars are interested in studying determinant problems and get many world-famous achievements. As early as in 1893， the famous mathematician Hadamard proposed the following well-known inequality:

Lemma 1(Hadamard inequality)[1]. LetA=(aij)bearealsymmetricpositivedefinitematrixofordern.Thendet(A)≤a11a22…annanddet(A)=a11a22…annifandonlyifA=(aij)isadiagonalmatrixorthereexistsarow(column)iszero．

In1907，FishergaveasharperinequalitycalledFisherinequalitywhichmakestheHadamardinequalitybecomeitsspecialcase.TheFisherinequalitycanbestatedasfollows:

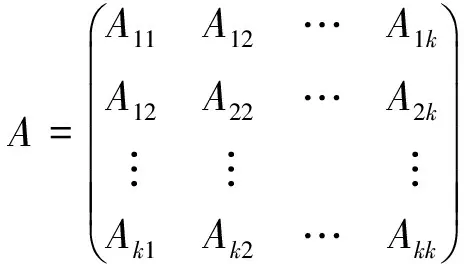
Lateron，variousformsofdeterminantinequalitiesarepresented.SuchasthefamousSchurdeterminantinequality，theM.Marcusdeterminantinequality，andtheOppenheimdeterminantinequality.

In2013，IMAGE51of“TheBulletinoftheInternationalLinearAlgebraSociety”[3]releasedadeterminantinequalityandasksforsolving.Inorderforexpression，werewritethisproblem:

Problem (Minghua Lin)[3]. LetA=(aij)bearealsymmetricpositivedefinitematrixofordernandletA(i)bethesubmatrixobtainedfromAbydeletingthei-throwandi-thcolumn.Showthatthefollowinginequalityholdsforn≥4andfailsforn=2，3:

(1)

In2014，MinghuaLingavethesolutiononIMAGE53ofthebulletin[4]，heprovedtheproblemaccordingtotheresultofMerris[5]andpointedoutheisstilllookingforthedirectproof.

Inthisarticle，wedirectlyprovethattheinequality(1)holdsforn=4andfailsforn=2， 3.Andthenweprovethatforaclassoftri-diagonalmatrices，theinequality(1)holdsforn≥3.WealsogiveanewHadamard-likeinequalitythatholdsforallHermitianmatricesofordern(n≥1)．

Throughout this paper，A(i，j)(i，j=1，2，…，n，i≠j)standsforthesubmatrixofAobtainedfromAbydeletingthei-throwandj-thcolumn.Especially，inordertobeconsistentwiththeoriginalproposition，weuseA(i)(i=1，2，…，n)todenotethesubmatrixofAobtainedfromAbydeletingthei-throwandi-thcolumn.Sincethematrixthatwediscussissymmetric，aji=aij(i，j=1，2，…，n)alwaysbetrue.

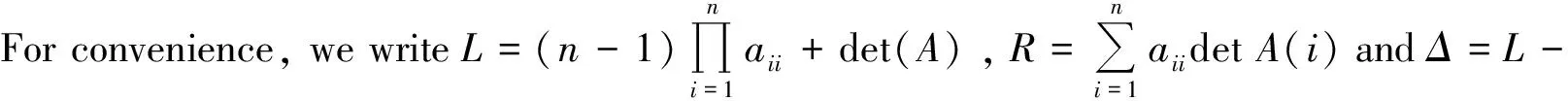
2The proof of Hadamard-like inequality failing for n=2，3 and holding for n=4

In fact， (1)’s reverse inequality holds forn=2.Thefollowingistheproof．

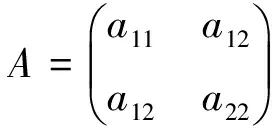
and

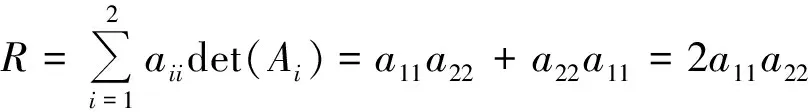
ThusL≤RandL=Rifandonlyifa12=0.

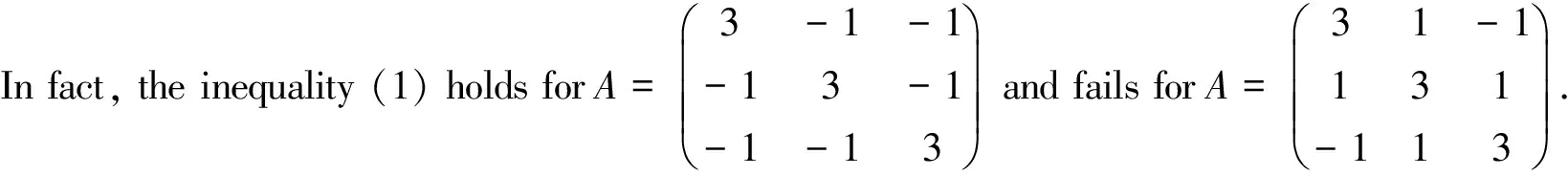
Next，weprovethattheHadamard-likeinequalityholdsforn=4，themethodofproofisstillprimary.

det(A)=a11detA(1)-a12detA(1，2)+a13detA(1，3)-a14detA(1，4).

BecauseofLandRcontainingthesameelementa11detA(1)，soweonlyneedtoprovethefollowinginequality:

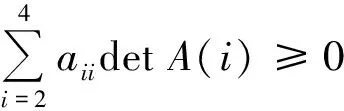
(2)

Bythecalculationruleofthedeterminant，wehavethefollowingresults:

a23a14a34+a13a24a34-a24a14a33)，

a12a24a34-a22a13a44+a22a14a34-a14a23a24)

and

a12a24a33-a22a13a34+a14a22a33+a13a23a24).

Sowededucethat

-a12detA(1，2)+a13detA(1，3)-

a14detA(1，4) =2a12a13a23a44+

2a12a14a24a33+2a13a14a22a34-

2a12a14a23a34-2a12a13a24a34

(3)

Andsince

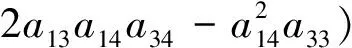
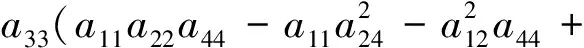
and

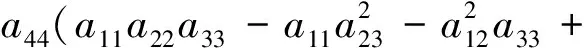
Wededucethat

a22detA(2)+a33detA(3)+a44detA(4) =

3a11a22a33a44+2a13a14a22a34+2a12a14a33a24+

(4)

By(2)～(4)Δcan be simplified as follows:

2(a12a13a24a34+a12a14a23a34+a13a14a23a24)+

(a12a34-a14a23)2+(a14a23-a13a24)2-

Next，wedetermineΔis whether positive or not.

SinceAisarealsymmetricpositivedefinitematrixandtheprincipalminorsofAisgreaterthanzero，thenwecanget

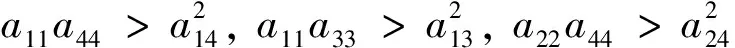
So

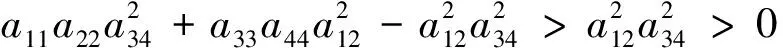
and

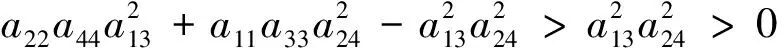
SoΔ≥0．

Thus we complete the proof．

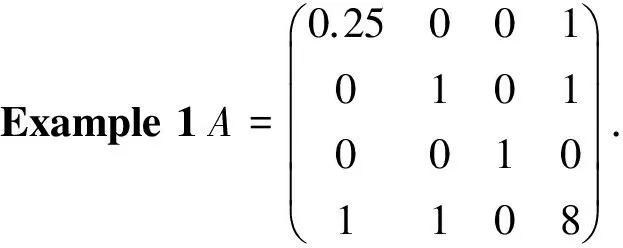
Then

，

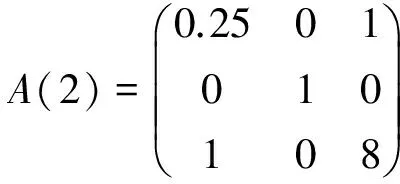
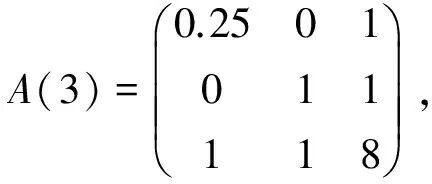
detA(1)=7， detA(2)=1， detA(3)=0.75， detA(4)=0.25， and det(A)=0.75．

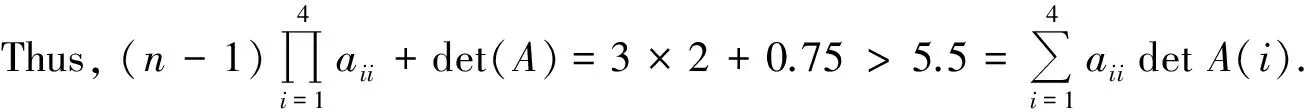
3The proof of Hadamard-like inequality holding for a kind of special matrix

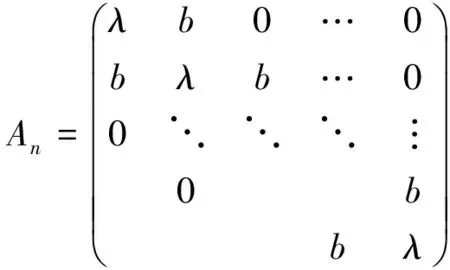
Firstly，wegiveaformulaofthegeneraltermofanbythefollowing:

an=(λ-m)xn-1+myn-1，

where

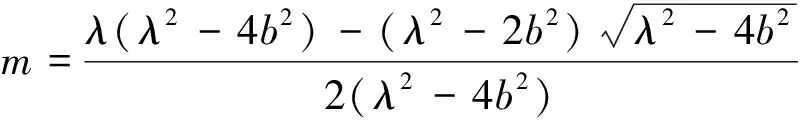
and

Proof According to the calculation rule of determinant， we can get the recursion formula ofan:an=λan-1-b2an-2.

Letan-xan-1=y(an-1-xan-2)，thenan=(x+y)an-1-xyan-2.Wededucethat

(5)

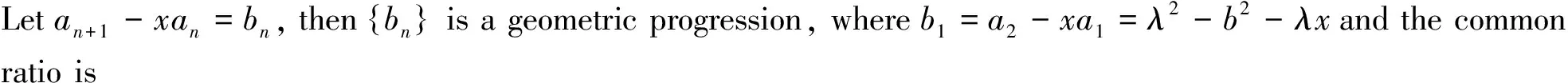
bn-1=an-xan-1=b1yn-2=(λ2-b2-λx)yn-2.

(6)

Further，consideringan-myn-1=x(an-1-myn-2)，wehave

an-xan-1=yn-2(my-mx).

(7)

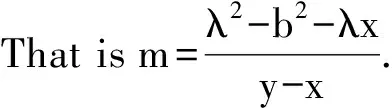
cn=an-myn-1=c1xn-1=(λ-m)xn-1.

(8)

Soan=(λ-m)xn-1+myn-1.

Thus，wecompletetheproof．

TheLemma3essentiallyprovidesacomputationalmethodforakindoftri-diagonalmatrix.

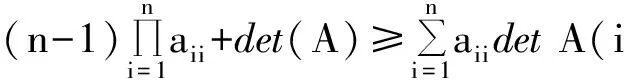
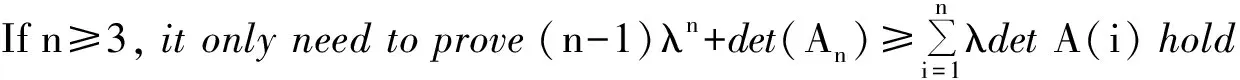
Sinceaiidet(Ai)=λai-1an-i，wededucethat

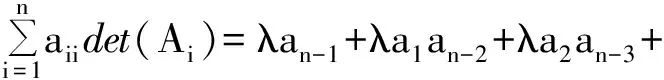
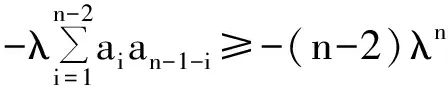
Thus，weonlyneedtoprovethefollowinginequalityholds:

(n-1)λn+an-2λan-1-(n-2)λn=

λn+an-2λan-1≥0.

(9)

AccordingtoLemma3，λ=x+yandan=(λ-m)xn-1+myn-1，then(9)canbesimplifiedinthefollowinginequality:

(x+y)n+(λ-m)xn-1+myn-1-

(x+y)n-xn-xn-1y+mxn-1-

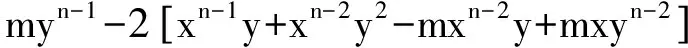
(10)

Sincex+y=λ，xy=b2，wecangetλ2-4b2=(x+y)2-4xy=(x-y)2and

λ2-2b2=(x+y)2-2xy=x2+y2．

Consequently，

Andbecauseof

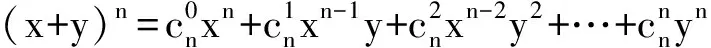
and

Thus，wecancontinuetocalculate(10)，wehave

(x+y)n+(λ-m)xn-1+myn-1-

(x+y)n-xn-xn-1y+mxn-1-

(x+y)n-xn-3xn-1y-2xn-2y2-

2xn-2y2-2xy3(xn-4+…yn-4)-

y2(xn-2+…yn-2)=

(11)

Thus，wecompletetheproof．

Example 2 IfA5hastheformasthebeginningofthischapter，letλ=3andb=1，thenA5ispositivedefinitematrix.Bythecalculationruleofthedeterminant，wecanget:L=4×35+144=1116andR=2×3×55+2×3×3×21+2×3×64=900.SoL>R．

Thus， (1)holdsforA5．

4 A new Hadamard-like inequality holding for all Hermitian matrices of order n (?n≥2 )

In this section， we give a derivative result that derived from our research process for the Hadamard-like inequality.

Lemma 4[2]LetA=(aij)beasemidefinitematrixofordern.Ifitsdiagonalelementsare

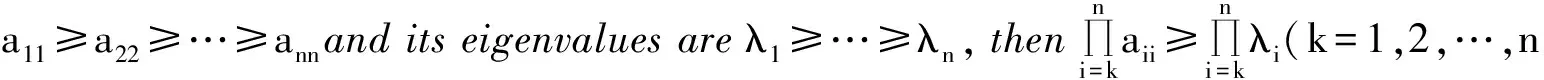
Lemma 5[2]LetA=(aij)beHermitianmatrixofordernandBbeitsmorderprincipalsubmatrix.Iftheireigenvaluesareλ1≥λ2≥…≥λnandμ1≥μ2≥…≥μmrespectively，then

λj≥μj≥λj+n-m，j=1，2，…，m.

Lemma 6[2]LetA=(aij)beHermitianmatrixofordern.Ifitseigenvaluesareλ1，λ2，…，λn，then(a11，a22，…，ann)(λ1，λ2，…，λn)．

Now，westateournewinequality．

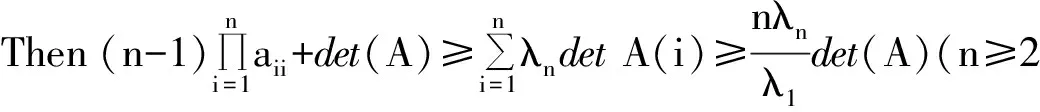
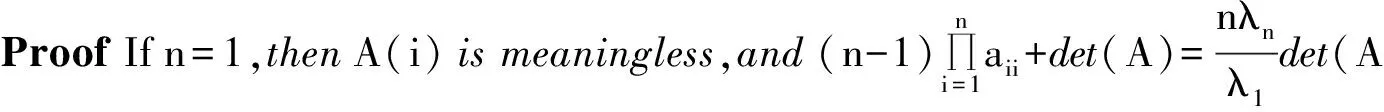
Letμ1i≥μ2i≥…≥μn-1i(i=1，2，…，n)betheeigenvaluesofA(i)andλ1≥…≥λnbetheeigenvaluesofA=(aij)，thenbyLemma5，wehaveλj≥μji≥λj+1，where

j=1，2，…，n-1，i=1，2，…，n．

Consequently，wehave

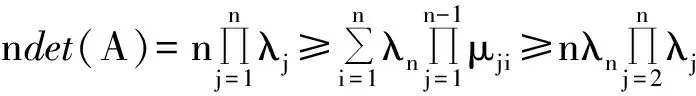
(12)

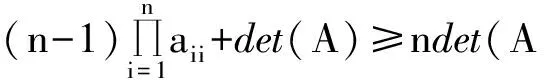
(13)

By(12)and(13)，wecandeducethat

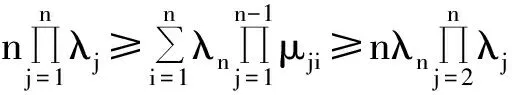
(14)

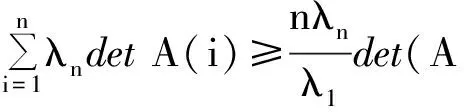
Thuswecompletetheproof．

[1] HOM R A， JOHNSON C R. Matrix Analysis [M]. Cambridge: Cambridge University Press， 1985．

[2] ZHAN X Z. Matrix Theory[M]. Beijing: Higher Education Press(In Chinese)， 2008.06.

[3] The Bulletin of the International Linear Algebra Society.IMAGE51.Fall 2013，41.[EB/OL] http://ilasic.org/IMAGE/.

[4] The Bulletin of the International Linear Algebra Society.IMAGE53.Fall 2014，45.[EB/OL] http://ilasic.org/IMAGE/．

[5] MERRIS R.Oppenheim’s inequality for the second immanant[J]. Canad Math Bull 1987， 30:367-369．

[6] ZHANG F. Matrix theory: basic results and techniques [J]. 2nd ed. New York: Springer，， 2011．

[7] CHEN S. Some determinantal inequalities for Hadamard product of matrices [J]. Linear Algebra Appl, 2003， 368: 99-106.

2016-08-23.

山西省重點課題研究項目(SSKLZDKT2014084).

1000-1190(2017)01-0012-06

關于Hadamard-like不等式

王菊平, 郭東星, 曹紅艷, 王淑玲, 張持晨

(山西醫科大學 數學教研室， 太原 030001)

給出了由林明華提出的Hadamard-like不等式問題的部分證明,用直接的方法證明了該不等式當n=2， 3 時不成立，當n=4 時成立以及對于特殊的三對角矩陣，該不等式當n≥3 時恒成立.最后，文中給出了一種新的Hadamard-like不等式，此種不等式對于任意的Hermitian矩陣當n≥2 成立.

Hadamard-like不等式； 行列式；Hermitian矩陣

O151

A

*通訊聯系人.E-mail:zhangchichen@sina.com.