基于Laguerre函數(shù)的船舶航向DMPC研究?

李光磊1郭亦平林莉

基于Laguerre函數(shù)的船舶航向DMPC研究?

李光磊1郭亦平2林莉2

（1.海軍駐九江地區(qū)軍事代表室九江332007）（2.中國船舶重工集團(tuán)公司第七○七所九江分部九江332007）

針對船舶在風(fēng)浪等環(huán)境干擾下頻繁打舵、控制偏差大的問題，從船舶運(yùn)動模型和模型預(yù)測控制入手，研究Laguerre函數(shù)的應(yīng)用，提出了一種基于Laguerre函數(shù)的船舶航向DMPC控制方法，設(shè)計(jì)了一種高海情下航向控制算法，并通過數(shù)字仿真驗(yàn)證了控制算法的有效性。

船舶；航向控制；模型預(yù)測控制；Laguerre函數(shù)

Class NumberTP212

1 引言

在大風(fēng)浪中航行的船舶受到風(fēng)、浪、流的干擾會產(chǎn)生航向偏差，通過操舵可以減小航向偏差，但風(fēng)浪的高頻干擾會激勵自動操舵儀或操舵人員頻繁地操舵以保持航向。理論研究和實(shí)操經(jīng)驗(yàn)表明，靜水中具有航向穩(wěn)定性的船舶在大風(fēng)浪中作定向直航時，會沿著某一航向作不規(guī)則的橫蕩和回轉(zhuǎn)運(yùn)動。此時往往不需要進(jìn)行操舵。不必要的操舵會消耗船舶的控制能量，加劇舵機(jī)的磨損；有些船舶由于控制參數(shù)選擇不合適等原因甚至?xí)霈F(xiàn)周期性的偏航，從而增加航程，加劇燃油消耗［1］。因而，研制在風(fēng)浪天氣打舵次數(shù)少，且航向控制精度高的自動操舵儀顯得尤為必要。

本文采用了基于Laguerre函數(shù)離散時間模型預(yù)測控制和基于海浪頻率跟蹤器的離散時間狀態(tài)觀測器相結(jié)合的方法，設(shè)計(jì)了一種高海情下航向控制算法，并通過構(gòu)建仿真環(huán)境驗(yàn)證了該算法具有風(fēng)浪天氣下航向精度高、打舵次數(shù)少的特點(diǎn)。

2 船舶運(yùn)動數(shù)學(xué)模型

船舶操縱運(yùn)動采用三自由度運(yùn)動方程［2～3］，其運(yùn)動方程式為

式中，X、Y、Mz可分別表示如下：

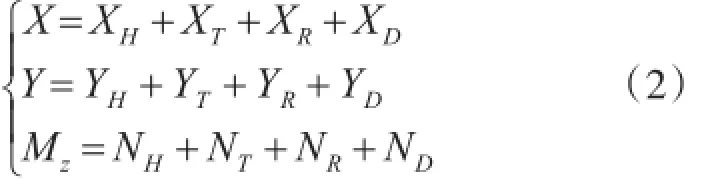
下標(biāo)H、T、R、D分別表示船體流體水動力和力矩、螺旋槳推力和推力矩、舵力和舵力矩，風(fēng)、浪、流等干擾的合力和合力矩。

波浪產(chǎn)生的干擾力和力矩在船體坐標(biāo)系上的投影可由下列公式確定：

式中ω為波浪平均頻率，在仿真計(jì)算時用ω=ωm/0.71來近似，ωm為頻譜的最高頻率，χy，χmz為與船舶結(jié)構(gòu)特性以及浪向角φw有關(guān)的換算系數(shù)，αw為波傾角。

3 基于Laguerre函數(shù)的航向DMPC控制器設(shè)計(jì)

3.1經(jīng)典模型預(yù)測控制概述

MPC是一種基于模型的控制算法［4］，其核心為：可預(yù)測過程未來行為的動態(tài)模型，在線反復(fù)優(yōu)化計(jì)算并滾動實(shí)施的控制作用和模型誤差的反饋校正［5］。其基本原理見圖1。

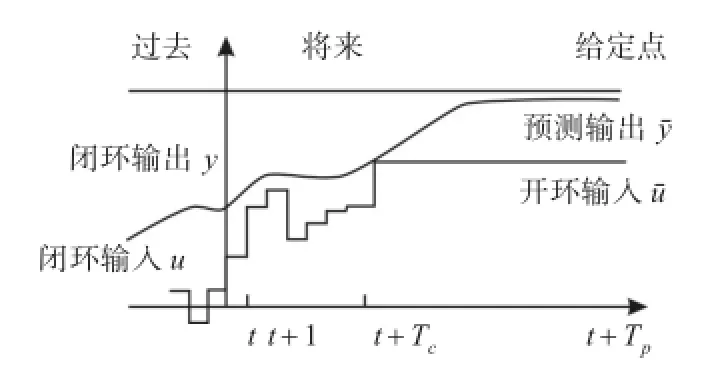
圖1 預(yù)測控制基本原理圖

預(yù)測模型的功能就是根據(jù)對象的歷史信息和未來輸入，預(yù)測其未來輸出，預(yù)測模型具有展示系統(tǒng)未來動態(tài)行為的功能。利用預(yù)測模型為MPC的優(yōu)化提供先驗(yàn)知識，決定采用何種控制輸入，使未來時刻被控對象的輸出變化符合預(yù)期的目標(biāo)。模型預(yù)測控制的特點(diǎn)是滾動優(yōu)化、滾動實(shí)施及反饋校正。

3.2Laguerre函數(shù)在DMPC設(shè)計(jì)中的應(yīng)用

離散時間Laguerre網(wǎng)絡(luò)［6］是由連續(xù)時間Laguerre網(wǎng)絡(luò)離散化產(chǎn)生，離散時間Laguerre網(wǎng)絡(luò)的z變換如下：

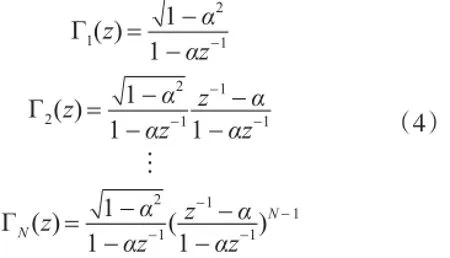
這里，a是離散時間Laguerre網(wǎng)絡(luò)的極點(diǎn)，且為保證網(wǎng)絡(luò)穩(wěn)定性，有0≤a＜1，稱作Laguerre網(wǎng)絡(luò)標(biāo)量因子。Laguerre網(wǎng)絡(luò)最知名的性能是它們的正交性。其頻域表示為

對于Γm(z),m=1,2,…,N，有

在模型預(yù)測控制中，為了尋找離散時間Laguerre函數(shù)，可利用Laguerre網(wǎng)絡(luò)的狀態(tài)控制實(shí)現(xiàn)來得到。

設(shè)上述Laguerre網(wǎng)絡(luò)中，l1(k)是Γ1(z,α)的反z變換，l2(k)是Γ2(z,a)的反z變換，…，lN(k)是ΓN(z,α)的反z變換，則該離散時間Laguerre函數(shù)集可用向量形式表示：

該函數(shù)集滿足下述差分方程

矩陣Al是(N×N)的，且是具有α和β=(1-α2)兩個參數(shù)的函數(shù)，其初始條件為

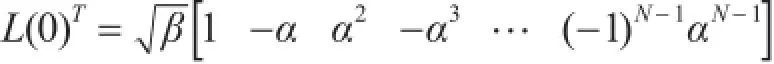
例如，當(dāng)N=5時

Laguerre網(wǎng)絡(luò)的正交性能時域表示為

假設(shè)一個穩(wěn)定系統(tǒng)的脈沖響應(yīng)為H(k)，則該響應(yīng)可用N階Laguerre函數(shù)表述為

這里，c1c2…cN是由系統(tǒng)數(shù)據(jù)決定的系數(shù)，該Laguerre網(wǎng)絡(luò)的系數(shù)由下式定義：

實(shí)際上，由于Laguerre函數(shù)的正交性能，這些系數(shù)也可最小化下述誤差平方和函數(shù)：

上述離散時間脈沖響應(yīng)的描述導(dǎo)致了使用Laguerre函數(shù)進(jìn)行預(yù)測控制的設(shè)計(jì)。

在使用脈沖算子的經(jīng)典DMPC設(shè)計(jì)中，ΔU對應(yīng)Laguerre函數(shù)多項(xiàng)式中α=0的情況。在快速采樣、復(fù)雜過程動態(tài)和高閉環(huán)性能指標(biāo)等情況下，若想獲得令人滿意的控制信號Δu，可能需要非常多的參數(shù)，這會導(dǎo)致較差的數(shù)值計(jì)算結(jié)果，產(chǎn)生沉重的計(jì)算負(fù)擔(dān)。因而，一種更適當(dāng)?shù)姆椒ㄊ窃谀Ｐ皖A(yù)測控制中使用Laguerre網(wǎng)絡(luò)。

在ki時刻，控制軌跡Δu(ki),Δu(ki+1), Δu(ki+2),…,Δu(ki+k)…被稱作穩(wěn)定動態(tài)系統(tǒng)的脈沖響應(yīng)，因而，可用Laguerre函數(shù)集來描述該動態(tài)響應(yīng)，在任一未來采樣間隔k，有

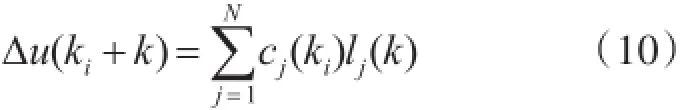
式中，ki為滑動時間窗的初始時刻，k為未來采用時刻，N為多項(xiàng)式階數(shù)，cj，j=1,2,…,N是Laguerre函數(shù)的系數(shù)，這些系數(shù)是滑動時間窗初始時刻ki的函數(shù)。當(dāng)α=0時，N=Nc，Nc為控制時域。

4 船舶航向DMPC控制器設(shè)計(jì)

4.1基于Laguerre函數(shù)的船舶航向DMPC算法設(shè)計(jì)

將式（1）和式（2）所示的船舶運(yùn)動數(shù)學(xué)模型抽取出橫向運(yùn)動和偏航運(yùn)動方程后線性化，并引入輔助方程Φ=r，可得船舶偏航運(yùn)動方程如下：

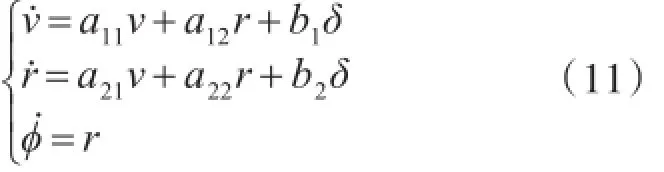
簡記為

式中

將式（12）離散化兩端差分運(yùn)算后，可得

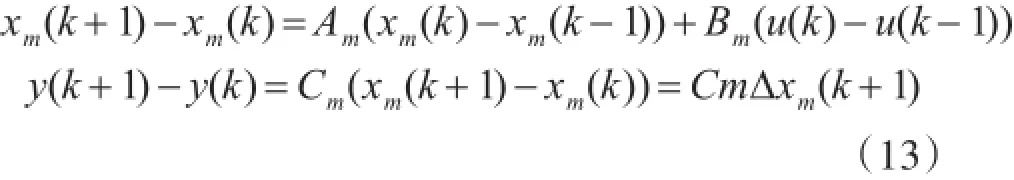
引入如下符號：

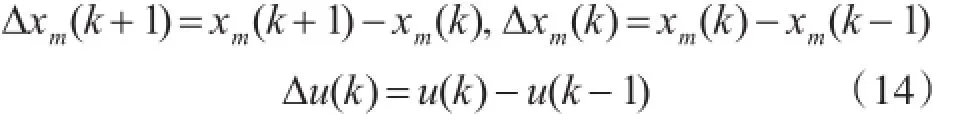
則可由式（14）得如下增量式狀態(tài)方程和狀態(tài)輸出方程：

上式簡記為

假設(shè)在k時刻的m個采樣間隔后解算的預(yù)測指令舵角增量為

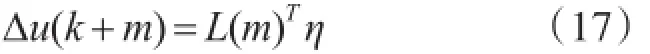
式中，L(m)T為擬合航向MPC控制器的離散化Laguerre函數(shù)向量，η為Laguerre參數(shù)。

假設(shè)在k時刻，式（16）的狀態(tài)為x(k)，則在此時刻的m個采樣間隔后的預(yù)測狀態(tài)為

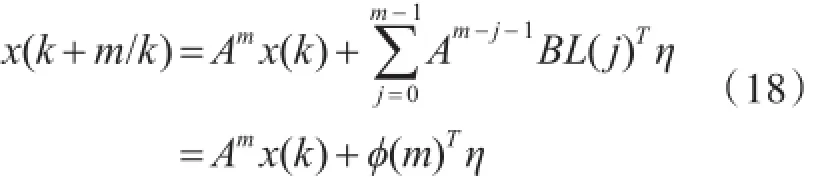
為解算航向預(yù)測控制律，設(shè)代價函數(shù)［7］為

則該代價函數(shù)的最優(yōu)解為

將式（20）代入式（17），可得

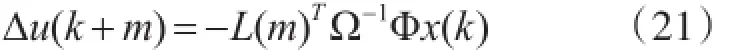
由此可得，在k時刻，航向MPC控制器的控制律為

式中，x(k)應(yīng)由觀測值替換。觀測器的設(shè)計(jì)可利用離散時間kalman估計(jì)理論設(shè)計(jì)。

4.2惡劣海況下航向?yàn)V波算法設(shè)計(jì)

4.2.1 海浪中心頻率的在線辨識

操舵導(dǎo)致的航向運(yùn)動為低頻運(yùn)動，海浪誘導(dǎo)的航向運(yùn)動為高頻運(yùn)動，因此，為了抑制由于海浪引起的航向變化對航向操縱控制的影響，應(yīng)對航向進(jìn)行濾波。航向?yàn)V波算法采用Fossen［8］提出的基于海浪頻率跟蹤器的kalman濾波算法［9］。

假設(shè)在海浪干擾作用下，由羅經(jīng)測得的航向角由兩部分組成：

由海浪誘導(dǎo)產(chǎn)生的航向角有如下關(guān)系式存在：

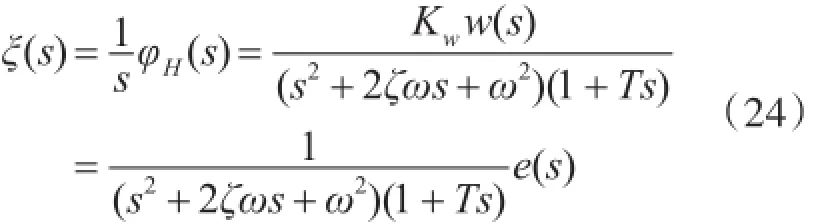
式中

由式（24）和式（25）可得

由此可知，將航向角低通濾波后得到ξ(s)，然后構(gòu)建AR模型對式（26）中相關(guān)參數(shù)進(jìn)行辨識。參數(shù)a1、a2和a3可利用具有遺忘因子的遞歸最小二乘法辨識得到。

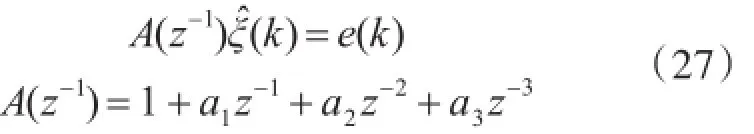
波浪頻率的估計(jì)可由解上述A(z-1)的根后轉(zhuǎn)化成連續(xù)時間根來獲得

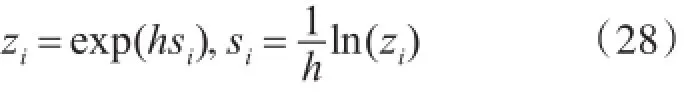
波浪頻率估計(jì)值為

4.2.2 帶有海浪擴(kuò)張狀態(tài)的航向?yàn)V波器設(shè)計(jì)

由式（29）獲得波浪主頻率的估計(jì)值后，可假設(shè)波浪誘導(dǎo)航向運(yùn)動狀態(tài)方程為

將式（16）、式（30）和式（23）聯(lián)立后，可得具有海浪擴(kuò)展?fàn)顟B(tài)的航向運(yùn)動狀態(tài)方程和輸出方程。則可利用kalman濾波原理設(shè)計(jì)航向運(yùn)動的離散時間濾波器。

將式（22）中的x(k)替換為對應(yīng)的觀測值后，航向運(yùn)動控制器設(shè)計(jì)完成。

4.3指令航向的柔化

在船舶航向MPC算法中，考慮到船舶操縱的動態(tài)特性，為了避免控制過程中出現(xiàn)指令航向信號的劇烈變化，可要求實(shí)際航向?(k)沿著一條期望的、平緩的曲線到達(dá)設(shè)定航向值?z，這條曲線被稱為參考軌跡?z(k)，它是指令航向值經(jīng)過在線柔化的產(chǎn)物［10］，本文采用一階指數(shù)變化形式

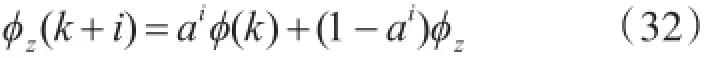
其中ai=，T為采樣周期，T為參考軌跡的時

s間常數(shù)，可取航向修正過程中最大航向變化率的倒數(shù)。

5 仿真驗(yàn)證與分析

5.1仿真試驗(yàn)

將設(shè)計(jì)好的DMPC控制器與船舶非線性數(shù)學(xué)模型及舵機(jī)數(shù)學(xué)模型構(gòu)成閉環(huán)控制系統(tǒng)，依次進(jìn)行平靜海況和5級海況下航速15kn和25kn的航向修正仿真試驗(yàn)。

1）平靜海況，初始航速15kn，航向修正30°仿真試驗(yàn)。

圖2 航向變化曲線

圖3 舵角變化曲線

2）平靜海況，初始航速25kn，航向修正30°仿真試驗(yàn)。

圖4 航向變化曲線

圖5 舵角變化曲線

3）5級海況，初始航速15kn，艏斜浪，浪向135°，航向修正30°仿真試驗(yàn)

圖6 航向變化曲線

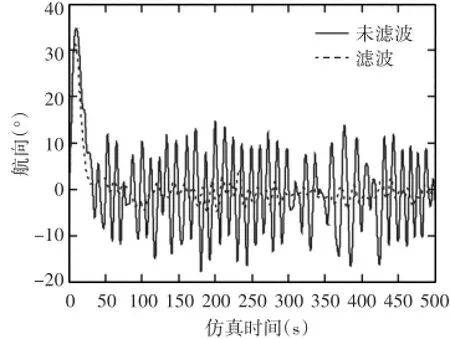
圖7 舵角變化曲線

4）5級海況，初始航速25kn，艏斜浪，浪向135°，航向修正30°仿真試驗(yàn)

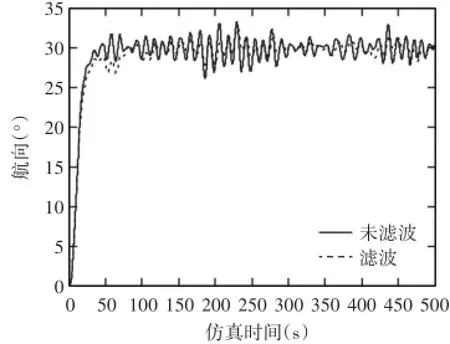
圖8 航向變化曲線

圖9 舵角變化曲線

5.2仿真分析

平靜海況下航向修正仿真試驗(yàn)結(jié)果的控制性能指標(biāo)統(tǒng)計(jì)結(jié)果見表1。由圖2、圖4和表1可以看出，本文提出的航向MPC算法在航向修正過程中回轉(zhuǎn)平穩(wěn)，超調(diào)量小，航向調(diào)整時間均不大于60s，航向穩(wěn)定誤差不大于0.3°。由圖3、圖5和表1可知，在整個航向修正過程中，出舵平穩(wěn)，出舵次數(shù)僅為2次。表明本文提出的基于Laguerre函數(shù)設(shè)計(jì)的MPC算法控制性能好，控制品質(zhì)高。

表1 平靜海況航向修正仿真試驗(yàn)控制性能統(tǒng)計(jì)表

表2 5級海況航向修正仿真試驗(yàn)控制性能統(tǒng)計(jì)表

5級海況下航向修正仿真試驗(yàn)結(jié)果的性能指標(biāo)統(tǒng)計(jì)結(jié)果見表2。由圖6、圖8和表2可知，本文設(shè)計(jì)的帶有海浪擴(kuò)張狀態(tài)的航向?yàn)V波器能夠較好地抑制波浪誘導(dǎo)的航向運(yùn)動而誘導(dǎo)的操舵，由表2可以看出，在濾波器接通狀況下，船舶在艏斜浪直航時，15kn航速下，最大偏航角較未濾波情況減小了1.3°，航向穩(wěn)定精度提高了0.239°，航向穩(wěn)定性能改善了16.2%，而最大出舵角由17.7°大幅減小到5.1°，平均出舵次數(shù)減少了42.4%，若以直航時平均出舵角作為操舵能量損耗指標(biāo)來衡量，則操縱能量損耗可降低75.5%；在25kn航速下，與未濾波情況相比，最大偏航角減小了0.9°，航向穩(wěn)定精度提高了0.444°，航向穩(wěn)定性能改善了36.3%，而最大出舵角減小了10.4°，平均出舵次數(shù)減少了32.3%，以直航時平均出舵角計(jì)，操舵能量損耗可降低73.84%。

6 結(jié)語

本文針對船舶在風(fēng)浪干擾條件下航行存在航向偏差大、操舵頻繁的問題，基于Laguerre函數(shù)設(shè)計(jì)了一種離散時間MPC控制算法和一種帶有海浪擴(kuò)張狀態(tài)的航向?yàn)V波算法，并在平靜海況和5級海況下開展了兩種不同航速下的仿真試驗(yàn)，綜合平靜海況和5級海況下仿真結(jié)果及分析可知，文中提出的航向MPC和濾波算法，具有良好的航向修正和航向保持性能，具有控制精度高、控制品質(zhì)好、打舵平穩(wěn)、能源損耗少的特點(diǎn)，完全能夠滿足船舶航海性能指標(biāo)要求。

［1］范尚雍.船舶操縱性［M］.武漢：海軍工程大學(xué)出版社，2004：32-42.

FAN Shangyong.The ship maneuvering［M］.Wuhan：Na?val Engineering University Press，2004：32-42.

［2］賈欣樂，楊鹽生.船舶運(yùn)動數(shù)學(xué)模型——機(jī)理建模與辨識建模［M］.大連：大連海事大學(xué)出版社，1999：141-167.

JIA Xinle，YANG Yansheng.Ship motion mathematical model——Modeling and identification mechanism model?ing［M］.Dalian：Dalian Maritime University Press，1999： 141-167.

［3］施生達(dá).潛艇操縱性［M］.北京：國防工業(yè)出版社，1995：200-232.

SHI Shengda.Submarine Maneuverability［M］.Beijing：National Defence Industry Press，1995：200-232.

［4］孫超，周湛鵬，郝曉辰，等.基于區(qū)間特性和變量軟約束的模型預(yù)測控制算法［J］.控制與決策，2015（10）：1879-1884.

SUN Chao，ZHOU Zhanpeng，HAO Xiaochen，et al.Model predictive control algorithm based on interval characteris?tic and variable soft constraint［J］.Control and decision，2015（10）：1879-1884.

［5］鄒濤，丁寶倉，張瑞.模型預(yù)測控制工程導(dǎo)論［M］.北京：化學(xué)工業(yè)出版社，2010：4-5.

ZOU Tao，DING Baocang，ZHANG Rui.An introduction to model predictive control engineering［M］.Beijing：Chemi?cal Industry Press，2010：4-6.

［6］Liuping Wang.Model Predictive Control System Design andImplementationUsingMATLAB?［M］.Spring?er-Verlag London Limited.2009：85-119.

［7］Tristan Perez.Ship Motion Control——Course Keeping and Roll StabilisationUsing Rudder and Fins［M］.Springer Science+Business media，2003：240-242.

［8］Thor I.Fossen.Guidance and Control of Ocean Vehiclesby［M］.New York：John Wiley&Sons Ltd，1994：242-245.

［9］吳瑤，羅雄麟.多率系統(tǒng)Kalman濾波算法的魯棒性分析［J］.自動化學(xué)報，2012（2）：156-174.

WU Yao，LUO Xionglin.Robustness Analysis of Kalman Filtering Algorithm for Multirate System［J］.Acta Auto?matica Sinica，2012（2）：156-174.

［10］D.W.Clarke，C.Mohtadi and P.S.Tuffs.Generalized Pre?dictive Control-PartⅠ.The Basic Algorithm［J］.Auto?matica，1987，23（2）：137-148.

Marine Course DMPC Control Based on Laguerre Function

LI Guanglei1GUO Yiping2LIN Li2
（1.Navy Military Representative Office in Jiujiang Area，Jiujiang332007）（2.Jiujiang Branch，The 707 Research Institute of CSIC，Jiujiang332007）

For the problem of frequently playing rudder and great control deviation when ships in the storm and other environ?mental disturbances，the application of the Laguerre function is studied by the ship motion model and model predictive control，and a ship heading DMPC control method based on Laguerre function is proposed，a course control algorithm under the high sea condi?tion is designed，the effectiveness of the control algorithm is verified through digital simulation.

ship，course control，model predictive control，Laguerre function

TP212

10.3969/j.issn.1672-9722.2017.05.042

2016年11月9日，

2016年12月31日

李光磊，男，碩士，工程師，研究方向：裝備管理，導(dǎo)航、制導(dǎo)與控制。郭亦平，男，碩士，高級工程師，研究方向：自動控制。林莉，女，博士，研究員，研究方向：自動控制。