帶乘性噪聲的廣義2D Ginzburg-Landau方程的漸近行為

楊 袁,舒 級,王云肖,李 倩,汪春江

(四川師范大學 數學與軟件科學學院,四川 成都 610066)

帶乘性噪聲的廣義2D Ginzburg-Landau方程的漸近行為

楊 袁,舒 級*,王云肖,李 倩,汪春江

(四川師范大學 數學與軟件科學學院,四川 成都 610066)

復Ginzburg-Landau方程是非線性科學中的重要模型,在物理學中的各個不同的分支都起著重要的作用.討論一類具乘性噪聲的隨機廣義2D Ginzburg-Landau方程的漸近行為,在Grauel H.和Flandoli F.(Probability Theory and Related Fields,1994,100:365-393.)建立的理論基礎上,運用先驗估計的方法加以證明.首先對方程的乘性噪聲項進行預處理,然后運用H?lder和Young不等式以及Gronwall引理給出方程在H和V中的吸收集的存在性,從而證明該方程所對應的隨機動力系統在L2中隨機吸引子的存在性.

隨機廣義2D Ginzburg-Landau方程; 隨機動力系統; 隨機吸引子; 乘性噪聲

1 預備知識

復Ginzburg-Landau方程是關于非平衡流體動力系統和化學系統的不穩定、超導和超流體、非線性光纖和Bose-Einstein凝聚及其空間模型描述的重要模型.目前已有許多關于2D Ginzburg-Landau方程的研究結果[1-10].對于如下廣義2D Ginzburg-Landau方程

(1)

其中,σ>0,ρ、γ、ν、μ、α、β均為實參數,λ1、λ2為復值向量;許多學者已經進行了廣泛而深入的研究.當σ=2時,文獻[1-2]分別討論了整體解的存在唯一性、指數吸引子、Gevery正則性、節點的個數以及它的慣性性質;文獻[3]討論了σ=3情形下整體解的存在性.

日前,含有高階項|u|6u的隨機2D Ginzburg-Landau方程,文獻[6]討論了在加性噪聲驅動下的隨機吸引子的存在性;但是同時含有|u|4u和|u|6u的乘性噪聲下的情形,還未見相關結論.

本文考慮如下具乘性噪聲的高階廣義2D Ginzburg-Landau方程

(2)

周期邊界條件和初始條件為:

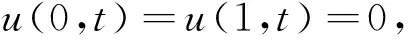
(3)

(4)

其中,u(x,t,ω)是未知復值函數,x∈D=(0,1)×(0,1),t>0,ω∈Ω,△是Laplace算子,σ>0,ρ、γ、ν、μ、α、β均為實參數,λ1、λ2為復值向量.方程(2)中的隨機函數W(t)是關于時間獨立的雙邊實值Wiener過程,它是定義在完備的概率空間(Ω,F,P)中,取值于L2(D)空間上的函數.

本文研究方程(2)～(4)對應的隨機動力系統的長時間行為.文獻[8-9]提出了隨機吸引子的概念,并被廣泛應用于文獻[11-13]中.文獻[14-15]討論了無界區域上隨機偏微分方程吸引子的相關問題,文獻[16-17]則關注了格上的隨機動力系統的漸進性質.

設(Ω,F,P)是一個概率空間.{θt:Ω→Ω,t∈R}是一族保測變換并且映射(t,ω)|→θtω是可測的,θ0=id,θt+s=θtθs,其中,s,t∈R,則θt是一個流;相應的概率空間(Ω,F,P,θt)被稱為可測的動力系統.進一步,假設θt是遍歷變換.

定義 1 設(X,d)是Polish空間(包含具有可數基的局部緊的Hausdorff空間),F是σ-代數,θ是(Ω,F,P)對應的保測變換,則可測映射φ:R+×Ω×X→X,(t,ω,x)|→φ(t,ω)x在X上P-a.s.滿足:

1)φ(0,ω)=id,

2)φ(t+s,ω)=φ(t,θsω)°φ(s,ω),?s,t∈R+(余環性質),

3)φ(t,ω):X→X連續;

就稱φ是一個連續的隨機動力系統.

定義 2 設(Ω,F,P)是概率空間,(X,d)是Polish空間,映射K:Ω→2X,{K(ω)}ω∈Ω是一族緊集,且對任意的x∈X,映射ω|→d(x,K(ω))依F可測,則稱{K(ω)}ω∈Ω為隨機緊集.

定義 3 設(Ω,F,P)是概率空間,(X,d)是Polish空間,φ是隨機動力系統,A(ω)是隨機集且有界集B?X,

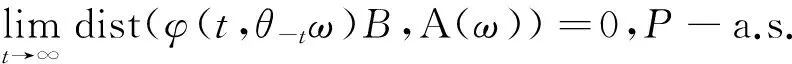
(b) 如果隨機集A(ω),P-a.s.滿足:

1) A(ω)是隨機緊集,對?ω∈Ω,A(ω)是緊的,并且對?x∈X,映射x|→dist(x,A(ω))可測;

2) A(ω)是不變集,即對t>0,φ(t,ω)A(ω)=A(θtω);

3) A(ω)吸引所有的確定集合B?X;

則隨機集A(ω)就是隨機動力系統的吸引子.

這里dist(·,·)代表Hausdorff半距離,其中

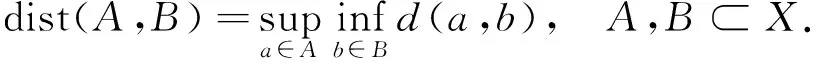
依照文獻[18-20]中的方法,可推出如下關于隨機吸引子的存在性定理.

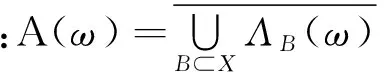
2 具乘性噪聲的高階廣義2D Ginzburg-Landau方程

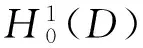
(5)

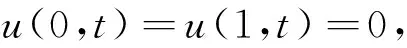
(6)

(7)

對方程(5)～(7)作如下變換:令v=z(t)u,其中z(t)=e-λW(t),則它滿足Stratonovich方程

(8)

所以有

du=z-2vdz+z-1dv.

(9)

于是方程(5)～(7)可改寫成如下形式:

(10)

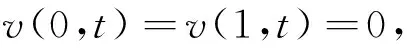
(11)

(12)

類似于文獻[7]中的定理5.1的證明,可知對任意ω∈Ω,方程(10)～(12)的解v的性質如下(在P-a.s.的意義下):

1) 對任意的v0∈H,方程(10)～(12)存在唯一的解v∈C([t0,T];H)∩C1([t0,T];H),?T<∞;

2) 如果v0∈D(A),則v∈C([t0,T];V)∩L2([t0,T];D(A)),?T<∞;

3) 對任意的t≥t0,映射v0=v(t0)|→v(t,ω;t0,v0)從H到H是連續的.

由以上結論,令

則S(t,ω)為乘性噪聲驅動下的隨機廣義2D Ginzburg-Landau方程(5)產生的隨機流.

3 隨機吸引子的存在性

下面首先給出本文的主要結果,即隨機吸引子的存在性定理.

定理 2 隨機2D Ginzburg-Landau方程(2)～(4)對應的隨機動力系統在L2(D)中存在一個緊的隨機吸引子A(ω).

為了證明定理2,需要先給出H和V中的吸收集的存在性.

3.1H中的吸收集

引理 1 假設v是方程(10)～(12)的解,則存在隨機半徑r1(ω),使得對?ρ>0,存在t(ω)≤-1,對所有的t0≤t(ω),u0∈L2(D)且‖u0‖<ρ,有以下不等式成立

其中

Q在證明中給定.

證明 令v與方程(10)在空間H上做內積并取實部得

(13)

由H?lder和Young不等式,等式右端后2項有:

則有以下不等式成立

(14)

記

則上式變為

注意到

(15)

其中

將(15)式代入(14)式得

對任意的t0≤t,t∈[-1,0],由Gronwall引理得

(17)

當t=-1時,有

(18)

記

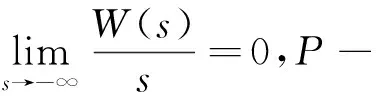
再由(18)式得

引理 2 下面不等式

成立,其中k1、k2、k3、g1(t)由下面證明中給出.

證明 令|v|6v與方程(10)在空間H上做內積并取實部,則有

(19)

首先方程(19)右邊第1項可估計

(20)

由H?lder和Young不等式,等式右端第2項有

(21)

方程(19)右邊第3、4項可分別估計:

(22)

(23)

方程(19)右邊第5項估計

由Gagliardo-Nienberg不等式可得:

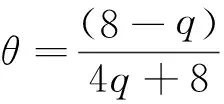
所以有

(24)

類似于第5項估計得到第6項估計

(25)

綜合(20)～(25)式,方程(19)變為

其中,k1=ε4+ε5,k2=ε1+ε3+ε6+ε7,k3=ε2+1+2,k4=l1+l2,g1=c(ρ,λ,ν,μ,γ,z)+c(1,l1,D,z)|3αλ1|16+c(2,l2,D,z)|αλ2|16.

3.2V中的吸收集

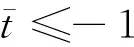
證明 將(10)式與△v作內積,再取實部得

(26)

由H?lder和Young不等式,等式右邊可估計為:

(27)

(28)

綜合(27)～(30)式,(30)式可變為

其中

再由引理2與(31)式可得

(32)

其中k6=k5δ,k7=k2+k5,g3(t)=g1(t)+g2(t).

可選取適當的k7和k6,使得

(33)

另外有

(34)

再選取合適的k3和k4,使得

綜合(33)～(35)式,(32)式可變為

(36)

又由引理1知

可得到

(37)

(36)式兩邊同時加上c1r1(ω)2,得到

使用Grownwall引理,對于t0≤s≤t可得

對于t=-1,s=t0,有

(39)

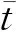
(40)

當t→-∞,g3(t)≥0至多多項式增長,從而r2是P-a.s.有限的,故有

隨機廣義2D Ginzburg-Landau方程產生隨機動力系統S,由引理1～3可得該隨機動力系統存在緊吸收集,應用定理1便證得定理2成立.

[1] 郭柏靈,高洪俊.廣義 Ginzburg-Landau 方程的有限維行為[J].自然科學進展,1994,4(4):423-434.

[2] DUAN J,HOLME P,TITI E S.Global existence theory for a generalized Ginzburg-Landau equation[J].Nonlinearity,1992,5:1303-1314.

[3] GUO B L,WANG X.Finite dimensional behavior for the derivative Ginzburg-Landau equation in two spatial dimensions[J].Physica:Nonlinear Phenomena,1995,D89(1):83-99.

[4] GUO B L,WANG G L,LI D L.The attractor of the stochastic generalized Ginzburg-Landau equation[J].Sci China:Math,2008,A51:955-964.

[5] LI D L,GUO B L.Asymptotic behavior of the 2D generalized stochastic Ginzburg-Landau equation with additive noise[J].Appl Math Mech,2009,30(8):883-894.

[6] 鮑杰,舒級.高階廣義2D Ginzburg-Landau方程的隨機吸引子[J].四川師范大學學報(自然科學版),2014,37(3):298-306.

[7] TEMAN R.Infinite-Dimensional Systems in Mechanics and Physics[M].New York:Springer-Verlag,1988.

[8] CRAUEL H,FLAUDOLI F.Attractors for random dynamical systems[J].Probability Theory and Related Fields,1994,100:365-393.

[9] CRAUEL H,DEBUSSCHE A,FRANCO F.Random attractors[J].J Dyn Diff Eqns,1997,9(2):307-341.

[10] 李棟龍,郭柏靈.帶附加噪聲的隨機廣義2D Ginzburg-Landau方程的漸進維行為[J].應用數學和力學,2009,30(8):883-894.

[11] ARNOLD L.Random Dynamical Systems[M].Berlin:Springer-Verlag,1998.

[12] DEBUSSCHE A.Hausdorff dimension of random invariant set[J].J Math Pur Appl,1998,77:967-988.

[13] ZHANG Q.Random attractors for a Ginzburg-Landau equaton with additive noise[J].Chaos Solitons and Fractals,2009,39:463-472.

[14] WANG Z J,ZHOU S F.Random attractor for stochastic reaction-diffusion equation with multiplicative noise on unbounded domains[J].J Math Anal Appl,2011,384:160-172.

[15] BATES P W,LU K N,WANG B X.Random attractors for stochastic reaction-diffusion equations on unbounded domains[J].J Diff Eqns,2009,246:845-869.

[16] WANG X H,LI S Y,XU D Y.Random attrcators for second-order stochastic lattic dynamical systems[J].Nonlinear Anal,2010,72(1):483-494.

[17] HUANG J H.The random attractor of stochastic FitzHugh-Nagumo equations in an infinite lattice with white noises[J].Physica:Nonlinear Phenomena,2007,D233(2):83-94.

[18] CRAUEL H.Global random attractors are uniquely determined by attracting deterministic compact set[J].Ann Math Pura Appl,1999,176:57-72.

[19] 張佳,舒級,董建,等.具乘性噪聲的隨機廣義Ginzburg-Landau 方程的隨機吸引子[J].四川師范大學學報(自然科學版),2015,38(5):638-643.

[20] 張元元,陳光淦.帶Robin邊界條件的2維隨機Ginzburg-Landau方程的吸引子[J].四川師范大學學報(自然科學版),2015,38(1):20-26.

2010 MSC:35B41; 35K05

(編輯 余 毅)

The Asymptotic Behavior of the Generalized 2D Ginzburg-Landau Equation with Multiplicative Noise

YANG Yuan,SHU Ji,WANG Yunxiao,LI Qian,WANG Chunjiang

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Complex Ginzburg-Landau equation,an important model in nonlinear science,plays a fundamental role in various branches of physics.In this paper,we consider the asymptotic behavior for genenralized 2D Ginzburg-Landau equation with multiplicative noise.The result is verified with a priori estimate which is based on the theory established by Crauel and Flandoli (Probability Theory and Related Fields,1994,100:365-393.).At first,we preprocess the multiplicative nosie terms.And then,with the Holder and Young inequalities and Gronwall Lemma,we obtain the existence of abstracting set when equations are inHandV.As a consequence,we prove the existence of random attractor of random dynamical system associated with the equation inL2(D).

Generalized 2D Ginzburg-Landau equation; random dynamical systems; random attractor; multiplicative noise

2016-05-30

四川省科技廳應用基礎計劃項目(2016JY0204)和四川省教育廳自然科學重點科研基金(14ZA0031)

O177.92

A

1001-8395(2017)02-0143-06

10.3969/j.issn.1001-8395.2017.02.001

*通信作者簡介:舒 級(1977—),男,副教授,主要從事隨機動力系統和偏微分方程的研究,E-mail:shuji2008@hotmail.com