帶有一階導數的脈沖微分方程多點邊值問題解的存在性

李海艷,李軍燕,李利玫

(1.四川大學 錦城學院,四川 成都 611731;2.四川師范大學 數學與軟件科學學院,四川 成都 610066)

帶有一階導數的脈沖微分方程多點邊值問題解的存在性

李海艷1,李軍燕1,李利玫2

(1.四川大學 錦城學院,四川 成都 611731;2.四川師范大學 數學與軟件科學學院,四川 成都 610066)

利用Leray-Schauder不動點定理討論一類非線性項與一階導數有關的二階脈沖微分方程的多點邊值問題,將以往所研究的方程的脈沖項和邊界條件作了改進,得到了解的存在性新結果.

Banach空間; 多點脈沖微分方程; 邊值問題; Leray-Schauder不動點定理

1 預備知識

脈沖微分方程是研究過程狀態發生突然變化動力學的基本工具,反映了微分方程在固定或不固定時刻的瞬時改變,因此能更真實廣泛地描述自然界性態.這一特點日益引起人們的重視,并將其廣泛應用于生物、醫療、社會、經濟、工程、物理、航空航天等諸多領域的研究[1-2].隨著人類的不斷進步與探究,脈沖微分方程方面的數學理論取得了重大進展,特別是邊值問題的研究愈來愈引起數學家們的重視,并有了非常豐富的研究成果,其中不乏多點邊值問題的討論[3-10].然而,帶有脈沖的邊值問題的研究[11-19]也逐漸成為一些學者研究的一個焦點,但是對帶有脈沖的多點邊值問題的研究[11-12]甚少.

文獻[10]利用Krasnoselskii不動點定理討論了如下多點邊值問題正解的存在性:

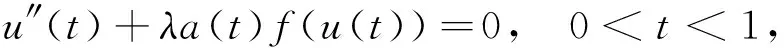
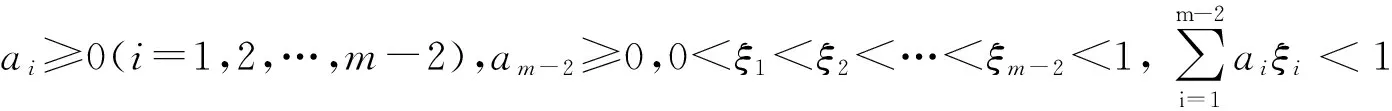
對于脈沖微分方程,文獻[11]研究了只含有導數脈沖的多點邊值問題

其中,J=[0,1],f∈C(J×R+,R+),Ik∈C(R+,R+),0<ξ1<ξ2<…<ξm-2<1,ai,bi∈(0,+∞),i=1,2,…,m-2.應用錐上的不動點定理獲得了多個正解的存在性定理.

受文獻[10-11]的啟發,本文討論了如下的二階脈沖微分方程的m-點邊值問題(BVP)

(1)

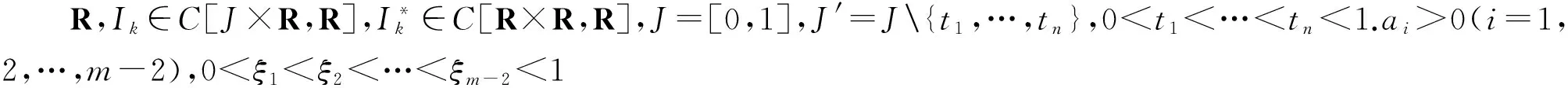
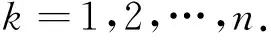
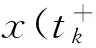
本文對文獻[10-11]所研究的方程的脈沖項做了改進,對其邊界條件進行了修改,并且在非線性項含有一階導數的情形下運用Leray-Schauder不動點定理獲得了該類問題解的存在性定理.

2 主要引理及其證明

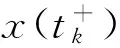
顯然,PC[J,R]在‖·‖PC下構成一個Banach空間,PC1[J,R]在‖·‖下構成一個Banach空間.

(2)

證明 設x是BVP(1)的解,對(1)式兩端積分

(3)

對(3)式再次積分得

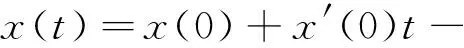
(4)

在(4)式中分別令t=1,t=ξi,則有

結合邊值條件有

即

所以

再結合(4)式可得(2)式.

反過來,假定x∈PC1[J,R]是脈沖微分方程(2)的解,易知

當t≠tk時,直接對(2)式求二階導數可得

和

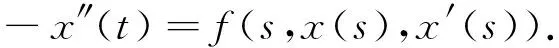
故x∈PC1[J,R]∩C2(J′),可以驗證

定義算子T:PC1[J,R]→PC1[J,R]如下

引理 2.2[20]集合H?PC1(J,R)是相對緊集的充分必要條件為H中的諸函數x(t)及其導函數x′(t)都在J上一致有界且在每個Jk(k=1,2,…,m)上等度連續.

由引理2.1和引理2.2可得引理2.3.

引理 2.3 算子T是從PC1(J,R)到PC1(J,R)的全連續算子.

引理 2.4[20](Leray-Schauder定理) 設X為實Banach空間,算子T:X→X為全連續算子,若集合{‖x‖|x∈X,x=λTx,0<λ<1}是有界的,則方程x=Tx至少有一個解.

3 存在性結果

定理 3.1 假設下列條件成立:

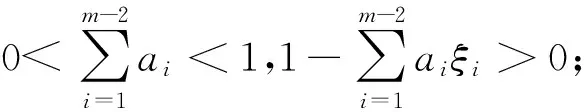
(H2) 存在常數M≥0,使得

(H3) 存在非負常數τk>0,ηk>0,使得

且

(H4) 存在常數βk>0,使得

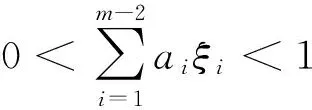
那么BVP(1)至少有一個解.

證明 由引理2.4可知,只需要證明方程

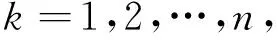
(5)

的解集在PC1(J,R)中有一個不依賴于λ的先驗界.

對?t∈J,由

可得

則

因為

所以

由此可知,只要‖x′‖有界,則‖x‖也有界.

接下來驗證‖x′‖的有界性.

為了計算方便,令x(t)=λ[x1(t)+I(t)],其中:

則有

當0≤t≤ξ1時

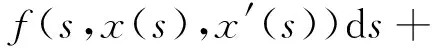
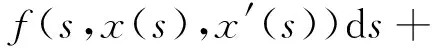
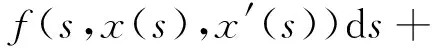
當ξr-1≤t≤ξr,2≤r≤m-2時

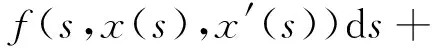
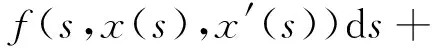
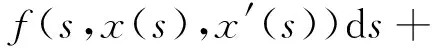
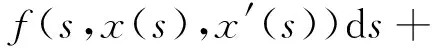
當ξm-2≤t≤1時

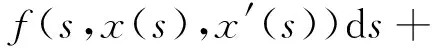
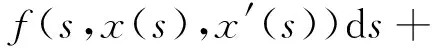
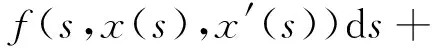
綜上,當0≤t≤1,ξi-1≤s≤min{ξi,t}時

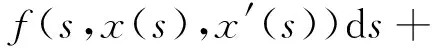
當0≤t≤1,max{ξi-1,t}≤s≤ξi時

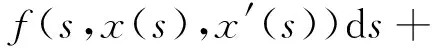
由上述討論可知,當ξi-1≤s≤min{ξi,t}時

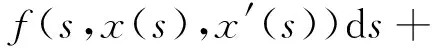
由(H1)可得

將上式中的s換成tk不等式也成立,從而可得

當max{ξi-1,t}≤s≤ξi時

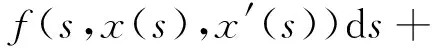
同理,由(H1)可得

將上式中的s換成tk不等式也成立,從而也可得

經過以上分析得

(6)

又已知

即

(7)

由(6)和(7)式得

(8)

由條件(H5),存在ε>0,滿足

由(H2),對上述ε>0,存在N>0,使得當0≤t≤1,‖x‖+‖y‖>N時有

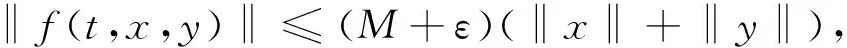
從而

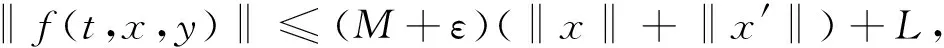
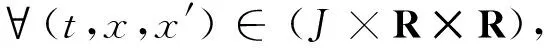
(9)

其中

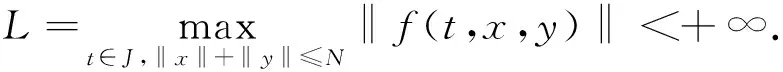
類似地,由(H4),對上述ε>0,存在Nk>0,k=1,2,…,n,使得當0≤t≤1,‖x‖+‖y‖>Nk時有

從而

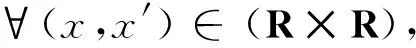
(10)

其中

現在,由(H3)以及(8)和(9)式可得

為了方便,引入記號

結合以上分析,易得對于?0<λ<1,都有

因此,‖x′‖有界,可得‖x‖也有界.故定理3.1得證.

[1] NENOV S.Impulsive controllability and optimization problems in population dynamics[J].Nonlinear Analysis:TMA,1999,36(7):881-890.

[2] KELLEY W G,PETERSON A C.Difference Equations:an Introduction with Applications[M].New York:Academic Press,1991.

[3] ZHANG G W,SUN J X.Positive solutions ofm-point boundary value problems[J].J Math Anal Appl,2004,291:406-418.

[4] JIANG W H,GUO Y P.Multiple positive solutions for second-orderm-point boundary value problems[J].J Math Anal Appl,2007,327:415-424.

[5] JIANG W H.The existence of positive solutions for second-order multi-point BVPs with the first derivative[J].Comput Math Appl,2009,225:387-392.

[6] WEI L,LIU Y X.Study on a kind of nonlinear neumann boundary value problems[J].Math Appl,2015,28(1):99-109.

[7] WEI L,LIU Y X.Research on the existence of solution of generalized curvature boundary value problems[J].Acta Math Scientia,2014,34(4):938-947.

[8] 李萍,舒級,張佳,等.一個具有相互作用非線性項的分數階微分方程組的爆破解[J].四川師范大學學報(自然科學版),2016,39(1):15-19.

[9] 涂馨予,蒲志林.一類帶一般記憶核的Cahn-Hilliard方程解的能量衰減估計[J].四川師范大學學報(自然科學版),2016,39(1):20-25.

[10] SUN Y P.Positive solutions of nonlinear second-orderm-point boundary value problem[J].Nonlinear Analysis,2005,61:1283-1294.

[11] FENG M Q,XIE D X.Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations[J].J Comput Appl Math,2009,223:438-448.

[12] LIU B,YU J S.Existence of solution for m-point boundary value problems of second-order differential systems with impulses[J].Appl Math Comput,2002,125:155-175.

[13] 魏君,蔣達清,祖力.一維p-Laplace二階脈沖微分方程的奇異邊值問題[J].應用數學學報,2013,36:414-430.

[14] 李耀紅,張曉燕.Banach 空間中一類二階非線性脈沖積分-微分方程邊值問題解的存在性[J].應用數學,2011,24(1):112-119.

[15] YAO M P,ZHAO A M,YAN J R.Anti-periodic boundary value problems of second order impulsive differential equations[J].Comput Math Appl,2010,59:3617-3629.

[16] YAO M P,ZHAO A M,YAN J R.Periodic boundary value problems of second-order impulsive differential equations[J].Nonlinear Analysis,2009,70:262-273.

[17] TIAN Y,JIANG D Q,GE W G.Multiple positive solutions of periodic boundary value problems for second order impulsive differential equations[J].Appl Math Comput,2008,200:123-132.

[18] ZHANG L L,ZHAI C B.Existence and uniqueness of positive solutions to nonlinear second order impulsive differential equations with concave or convex nonlinearities[J].Discrete Dyn Nat Society,2013,2013:1-11.

[19] JIANG W H,ZHANG Q,GUO W W.Multiple positive solutions for second order impulsive differential equation[J].Electron J Qual Theory Diff Eqns,2013(6):1-11.

[20] 郭大均.非線性分析[M].濟南:山東科技出版社,2001.

2010 MSC：34B10; 34B37

(編輯 李德華)

The Existence of Solutions for Multi-point Boundary Value Problem of Impulsive Differential Equations with the First Derivative

LI Haiyan1,LI Junyan1,LI Limei2

(1.DepartmentofMathematics,CollegeofJincheng,SichuanUniversity,Chengdu611731,Sichuan;2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

This paper studies the existence of solutions for multi-point boundary value problem of second-order impulsive differential equations with the first derivative.The boundary value conditions and impulsive term are extended.By using Leray-Schauder fixed-point theorem,the new conclusions about the existence of the solution are obtained.

Banach space; multi-point impulsive differential equation; boundary value problem; Leray-Schauder fixed point theorem

2015-12-07

四川省教育廳自然科學青年基金(12ZB108)

李海艷(1983—),女,講師,主要從事非線性泛函分析的研究,E-mail:jclihaiyan2012@163.com

O175.8

A

1001-8395(2017)02-0163-09

10.3969/j.issn.1001-8395.2017.02.004