求解波動方程的2種顯式高精度緊致差分格式
姜蘊芝,葛永斌
(寧夏大學 數學統計學院,寧夏 銀川 750021)
求解波動方程的2種顯式高精度緊致差分格式
姜蘊芝,葛永斌*
(寧夏大學 數學統計學院,寧夏 銀川 750021)
針對一維波動方程,空間采用四階Padé逼近,時間采用中心差分離散得到了一種時間二階、空間四階精度的顯式緊致差分格式,其截斷誤差為O(τ2+h4).之后采用截斷誤差余項修正的方法對時間離散進行改進,改進后的格式的截斷誤差為O(τ4+τ2h2+h4),即格式具有整體四階精度.然后,通過Fourier方法分析了2種格式的穩定性.最后,通過數值實驗驗證了本格式的精確性和可靠性.
波動方程; Padé逼近; 緊致格式; 顯式差分; 穩定性
波動方程是一類重要的雙曲型偏微分方程,在數學、物理、化學等領域內有著廣泛的應用[1].對這類方程進行數值求解的方法主要有有限差分法、有限元法和有限體積法等.就有限差分法而言,對該類問題研究的理論成果有:文獻[2]采用二階中心差分格式和非均勻網格離散,提出了一種求解一維波動方程在非均勻時間網格上的三層顯式差分格式,該格式具有一階精度;文獻[3]利用泰勒級數展開及待定系數法建立了一種求解一維波動方程的三層隱格式,該格式是條件穩定的,并且具有四階精度;文獻[4]將Runge-Kutta方法應用到哈密頓系統中并與辛格式相結合,提出了求解一維波動方程的一類顯式辛方法,該方法具有二階精度,并且是條件穩定的;文獻[5]采用三次樣條公式推導出精度分別為O(τ2+h2)、O(τ2+h4)、O(τ4+h2)和O(τ4+h4)的4種差分格式,并采用Fourier方法分析了格式的穩定性;文獻[6]對一維二階波動方程提出了具有二階精度的精細時程積分法,該方法能夠在時間方向上精確計算,空間方向的局部截斷誤差為O(h2),并且該方法是無條件穩定的;文獻[7]通過加權平均和緊致差分離散的思想提出了2種精度分別為O(τ2+h4)和O(τ4+h4)的隱式緊致差分格式;文獻[8]在Crank-Nicolson格式的基礎上設計了重疊型區域分解的并行算法,該算法的最優逼近階為O(τ2+h2);文獻[9]利用三次樣條插值,提出了求解一維波動方程的一種三層隱式差分格式,該格式最優能夠達到時間二階,空間四階精度,并且是無條件穩定的;文獻[10]通過四次樣條函數與廣義梯形算法相結合的方法提出了一維波動方程的一類兩層差分格式,其精度為O(τ2+h4),當選擇適當的參數時,其精度可提高到O(τ3+h4);文獻[11]采用四階緊致差商逼近公式及加權平均思想,提出了2種精度分別為O(τ2+h4)和O(τ4+h4)的交替方向隱式格式,前者是無條件穩定的,后者是條件穩定的;文獻[12]提出了一種求解一維波動方程的高精度隱式差分格式,該格式是無條件穩定的,并且具有時間二階、空間四階精度.本文將建立2種顯式緊致差分格式,為此,考慮如下一維波動方程的初邊值問題:

(1)

(2)
(3)
其中,u(x,t)是待求未知函數,a為波動系數,f(x,t)為非齊次項,φ(x)、ψ(x)、g0(t)、g1(t)為已知函數,且具有充分的光滑性.
1 顯式緊致差分格式的構造

1.1 CTFS格式對初始時間層的離散.利用泰勒展開公式有
(4)
將(2)式代入(4)式中,進行整理并舍去其截斷誤差項有
(5)

(6)
對于空間邊界節點的處理,由(1)式與(3)式可得
(7)
(8)
(9)
對上式進行整理,并舍去其截斷誤差項有

(10)

1.2 FTFS格式為了使時間精度與空間精度能夠相匹配,使格式整體精度達到四階,下面對上述差分格式進行改進,進一步提高時間精度,為此,對初始時間層的離散采用文獻[7]中的方法,有
(11)
其中λ=τ/h.對于時間二階導數項的離散,采用中心差分格式離散后保留其截斷誤差主項,可得
(12)
又由(1)式可得
(13)
將上式代入(12)式中有
(14)
對(14)式進行整理,并舍去其截斷誤差項有
又由(1)式,對上式進行變形有
(15)
(15)式即為整體四階精度的顯式緊致差分格式,記為FTFS格式.由格式的構造過程可知,該差分格式的截斷誤差為O(τ4+τ2h2+h4).
2 穩定性分析

引理 1[1]實系數二次方程μ2-bμ-c=0的根按模不大于1的充分必要條件為|b|≤1-c≤2.
對于(6)式有
(16)
對上式進行化簡整理有
(17)
(18)
令Uj=(uj,vj)T,并將(17)式代入進行整理有
(19)
從而可得CTFS格式(10)的誤差增長矩陣為
(20)
令λ=τ/h,r=aλ,則得上述誤差增長矩陣的特征方程為
(21)

(22)

(23)

(24)
將(17)式代入(24)式進行整理,可得FTFS格式的誤差增長矩陣為
(25)
則誤差增長矩陣的特征方程為
(26)
其中


因此,可得該格式穩定的充要條件為
(27)
上式等價于如下2個不等式:
(28)
對于不等式(28)易得
(30)
由于不等式對任意ω的取值都要成立,所以有
(31)

對于不等式(29),由求根公式易得其等式解為
(32)

(33)

3 數值算例
為了驗證本文所提2種格式的精確性和可靠性,現考慮如下2個具有精確解的初邊值問題.
問題 1[7]:

其精確解為u(x,t)=sin(πt)sin(πx).
問題 2 :
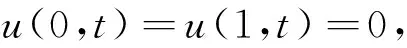
其精確解為u(x,t)=te-πtsin(πx).
表1~3給出了問題1的計算結果.表1采用本文CTFS格式與文獻[7]中的四階格式進行了計算.由于這2種格式的精度均為時間二階、空間四階,因此取τ=2h2,計算了t=0.5時刻取不同h時(τ也相應不同)的L∞和L2范數誤差和收斂階.eL∞和eL2范數及收斂階的定義如下:

(34)

(35)

(36)
由表1的數據可以看出,2種格式空間均達到了四階精度,而本文的CTFS格式要比文獻[7]中的四階格式更為精確.表2給出了本文FTFS格式和文獻[7]中的四階格式的計算結果,由于2種格式均具有整體四階精度,因此取τ=h,計算了t=0.5時刻取不同h時的L∞和L2范數誤差和收斂階.可以看出,2種格式幾乎具有相同的精度.


因此,當|a|λ大過1之后,計算結果是發散的.

表1 問題1當τ=2h2時,在t=0.5時刻對不同h的L2和L∞范數誤差及收斂階Table 1 The L2,L∞ norm error and the convergence rate with τ=2h2 at t=0.5 for different h for Problem 1
注:1.46E-3=1.46×10-3,下同.

表2 問題1當τ=h時,在t=0.5時刻對不同h的L2和L∞范數誤差及收斂階Table 2 The L2,L∞ norm error and the convergence rate with τ=h at t=0.5 for different h for Problem 1

表3 問題1當h=1/32時,對不同λ的L∞范數誤差Table 3 The L∞ norm error with h=1/32 for different λ for Problem 1
表4~6給出了問題2的計算結果.


表4 問題2當τ=h2時,在t=1時刻對不同h的L2和L∞范數誤差及收斂階Table 4 The L2,L∞ norm error and the convergence rate with τ=h2 at t=1 for different h for Problem 2

表5 問題2當τ=h時,在t=1時刻對不同h的L2和L∞范數誤差及收斂階Table 5 The L2,L∞ norm error and the convergence rate with τ=h at t=1 for different h for Problem 2

表6 問題2當h=1/32時,對不同λ的L∞范數誤差Table 6 The L∞ norm error with h=1/32 for different λ for Problem 2
4 結論

致謝 寧夏大學自然科學基金項目(ZR1407)和寧夏大學研究生創新項目(GIP2016032)對本文給予了資助,謹致謝意.
[1] 戴嘉尊,邱建賢.偏微分方程數值解法[M].南京:東南大學出版社,2002.
[2] CHO C H.Stability for the finite difference schemes of the linear wave equation with nonuniform time meshes[J].Num Meth Part Diff Eqns,2013,29(3):1031-1042.
[3] 張天德,孫傳灼.關于波動方程的差分格式[J].山東工業大學學報,1995,25(3):283-287.
[4] 孫耿.波動方程的一類顯式辛格式[J].計算數學,1997,19(1):1-10.
[5] 齊遠節,劉利斌.求解二階波動方程的三次樣條差分方法[J].大學數學,2011,27(1):59-64.
[6] 金承日,呂萬金.二階雙曲型方程的精細時程積分法[J].計算力學學報,2003,20(1):113-115.
[7] 葛永斌,朱琳,田振夫.求解波動方程的高精度緊致隱式差分方法[J].寧夏大學學報(自然科學版),2005,26(4):297-299.
[8] 田敏,羊丹平.波動方程的重疊型區域分解并行有限差分算法[J].山東大學學報(理學版),2007,42(2):28-38.
[9] RASHIDINIA J,JALILIAN R,KAZEMI V.Spline methods for the solutions of hyperbolic equations[J].Appl Math Comput,2007,190(1):882-886.
[10] LIU T,LIU L,XU H,et al.A new two level difference scheme for solving one-dimensional second-order hyperbolic equations[C]//2012 Fifth International Joint Conference on Computational Sciences and Optimization,2010:218-221.
[11] 馬月珍,李小剛,葛永斌.二維波動方程的高精度交替方向隱式方法[J].四川師范大學學報(自然科學版),2010,33(2):179-183.
[12] 崔進,吳宏偉.一類波動方程初邊值問題的高階差分格式[J].應用數學,2014,27(1):166-174.
[13] LELE S K.Compact finite difference schemes with spectral-like resolution[J].J Comput Phys,1992,103(1):16-42.
[14] 葛永斌,吳文權,田振夫.二維波動方程的高精度隱格式及其多重網格算法[J].廈門大學學報(自然科學版),2003,42(6):691-696.
[15] 余躍玉.一種Caputo型時間分數階波動方程的差分方法[J].四川師范大學學報(自然科學版),2014,37(4):524-528.
2010 MSC:35A35; 65M99
(編輯 陶志寧)
Two Kinds of Explicit High Order Compact Difference Schemes for Solving Wave Equations
JIANG Yunzhi,GE Yongbin
(CollegeofSchoolofMathematicalandStatistics,NingxiaUniversity,Yinchuan750021,Ningxia)
In this paper,an explicit compact difference scheme is obtained for solving the one dimensional wave equation.The truncation error of the scheme isO(τ2+h4).It’s constructed by applying the fourth-order accurate Padé approximation in space and the second-order accurate central difference in time.Then,the remainder of the truncation error correction method is employed to improve the accuracy of the discretization of time,the truncation error of the improved scheme isO(τ4+τ2h2+h4),which means the scheme has an overall fourth-order accuracy.And then,the stability conditions of the two schemes are obtained by the Fourier method.Finally,the accuracy and the reliability of the present two schemes are verified by numerical experiments.
wave equation; Padéapproximation; compact scheme; explicit difference; stability
2015-01-16
國家自然科學基金(11361045)
O242.1
A
1001-8395(2017)02-0177-07
10.3969/j.issn.1001-8395.2017.02.006
*通信作者簡介:葛永斌(1975—),男,教授,主要從事偏微分方程數值解法和計算流體力學的研究,E-mail:gyb@nxu.edu.cn

