基于雙派克變換的新型三相鎖相環技術*

李研達

(安陽師范學院 a. 物理與電氣工程學院， b. 河南省光伏并網發電及儲能技術工程實驗室， 河南 安陽 455000)

基于雙派克變換的新型三相鎖相環技術*

李研達a，b

(安陽師范學院 a. 物理與電氣工程學院， b. 河南省光伏并網發電及儲能技術工程實驗室， 河南 安陽 455000)

針對電網電壓不平衡故障時，三相鎖相環輸出存在二倍頻諧波擾動問題，提出了一種基于雙派克變換的新型鎖相環.對電壓信號分別進行正序派克變換和負序派克變換，并將負序派克變換中的直流量乘以變換矩陣，通過交叉解耦可消除正序派克變換中的二倍頻分量，有效提取了基波正序直流分量，可實現電網電壓不平衡條件下的相位和頻率準確跟蹤.在Matlab/Simulink環境中建立了仿真模型，分析了鎖相環在電網不平衡下的穩態響應.結果表明，本文提出的鎖相環較傳統的鎖相環而言，在電網故障下更能精確檢測電壓相位和頻率信息.

鎖相環； 三相不平衡； 二倍頻； 雙派克； 正負序分量； 直流量； 交叉解耦

鎖相環能夠有效檢測電網電壓信號的幅值、相位和頻率等信息，目前被廣泛應用于新能源并網變流器的控制算法中，以實現新能源變流器的輸出電流與電網電壓同步[1-2].在并網變流器控制中，通常將三相電流信號轉換成正交的兩直流信號進行控制，以達到PI無靜差控制，其中從三相轉換到兩相的參考相位都來自于鎖相環，因此，鎖相環的輸出精度對電流信號轉換起到了至關重要的作用[3].為提高新能源并網的穩定性和可靠性，對鎖相環功能提出了更高的要求，需要鎖相環在各類擾動下均能有效地跟蹤電網電壓正序分量的幅值、相位和頻率，同時具有較高的檢測精度和響應時間.

鑒于鎖相環在新能源并網控制中的重要性，國內外學者展開了一系列研究.文獻[4-6]介紹了基于過零鑒相器的鎖相環，通過檢測電網電壓的過零點和周期實現電網電壓相位的跟蹤，但是當電網電壓處于擾動情況下會對過零點的檢測產生影響，使結果存在一定的偏差；文獻[5-7]提出了一種基于乘法鑒相器的鎖相環，將輸出信號和輸入信號相乘，并通過濾波再經PI控制器即可得到輸出相位信號，以實現鎖相功能，此方法簡單易于實現，但環路濾波器的帶寬需設計的很窄，不利于響應速度；文獻[8-9]提出了一種基于同步坐標系的鎖相環，根據派克變換實現三相到兩相同步旋轉坐標系的轉換，通過控制無功分量即可實現鎖相.該鎖相環在電網電壓平衡時，能夠取得較好的鎖相效果，然而在電網電壓出現擾動導致三相不平衡時，輸出因含負序分量而導致出現大量的二次諧波分量，從而影響系統的穩定性.上述研究在理想電網情況下都具有較好的穩態和動態特性，但是當電網處于不平衡擾動時，如何保證輸出的穩定性和精確性，給鎖相環的設計帶來了一定的挑戰.本文提出一種基于雙派克變換的新型三相鎖相環，對電網電壓信號分別進行正序派克變換和負序派克變換，提取了基波正序直流分量，從而準確跟蹤電網電壓不平衡條件下的相位和頻率信息，并用Matlab/Simulink軟件進行了仿真驗證.

1 設計原理

實際的電網電壓會因各種故障或擾動而導致不平衡，而不平衡的電網電壓會導致鎖相環的輸出產生各種誤差，從而影響新能源并網系統的穩定性[10].電網電壓在不平衡情況下的表達式為

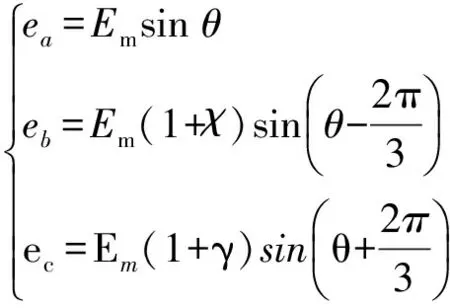
(1)

式中：ea、eb、ec為電網三相實際電壓；Em為電網電壓正常時的幅值；θ為a相電壓的相位；χ和γ分別為不平衡常數.式(1)在兩相坐標系中的表達式為

(2)

式中，eα、eβ為電網電壓在靜止坐標系下的電壓.由式(2)可以看出，當電網電壓處于三相不平衡時，兩相靜止坐標系下的分量不是完全正交的.根據派克變換，式(2)在兩相旋轉坐標系下q軸表達式為

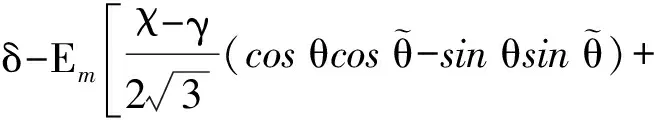
(3)

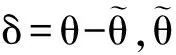
(4)

從式(4)可以看出，鎖相環輸出的無功直流分量因電網電壓不平衡而產生了電網電壓兩倍頻率的誤差信號，該誤差信號的幅值和電網電壓基波信號幅值相等，會給鎖相環的輸出精度帶來較大的誤差.針對二倍頻誤差信號，可利用低通濾波器將其濾除，但截止頻率設計過低會影響鎖相環輸出的動態性能.

2 雙派克變換的三相鎖相環

為了解決上文描述中的二倍頻問題，本文提出了一種基于雙派克變換的三相鎖相環.根據電路原理中三相穩態電路的基本思想，可將任意三相信號分解為對稱的三相正序分量、三相對稱的負序分量以及三相對稱的零序分量[11-12].對于零序分量而言，其不影響輸出結果，可不考慮，故只需對分解的正序分量和負序分量分別進行正序派克變換和負序派克變換，將其分解為直流分量和二倍頻交流分量.

對輸入信號進行兩次坐標變換，即對輸入信號的正負序分量分別進行派克變換可得

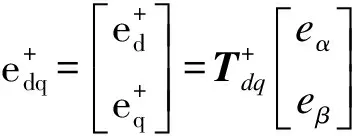
(5)

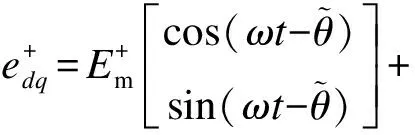
(6)

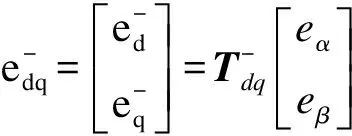
(7)

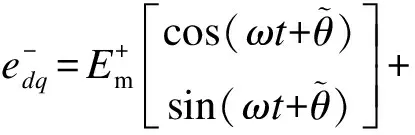
(8)

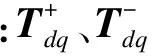
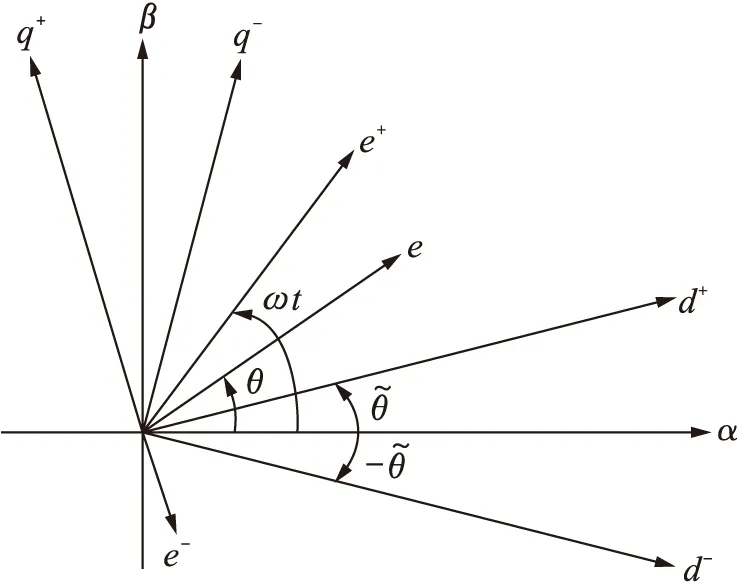
圖1 雙同步坐標變換中的電壓矢量圖

根據假設條件及坐標關系，可得到近似關系式，即

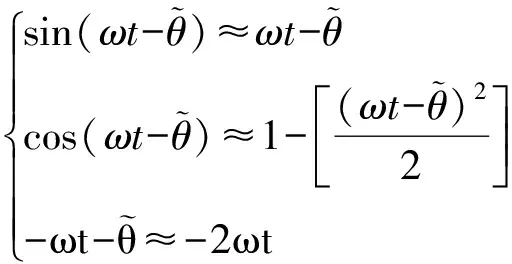
(9)

將式(9)代入式(6)和式(8)可得

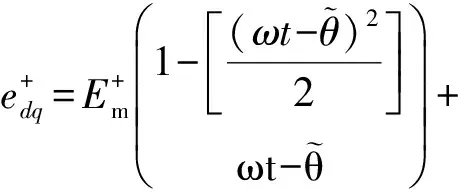
(10)

(11)

由式(10)和式(11)可以看出，正序派克變換中的二倍頻分量是由負序派克變換的幅值分量乘以變換矩陣得到的，負序派克變換中的二倍頻分量是由正序派克變換的幅值分量乘以變換矩陣得到.因此，可以將上述二倍頻分量通過交叉解耦進行消除，解耦后靜止坐標系下的正序分量則為

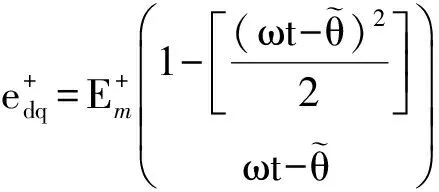
(12)

所以只需要控制旋轉坐標系下的q軸分量為零，即可實現電網電壓在不平衡狀況下的相位跟蹤.

基于上述分析，本文提出的雙派克變換鎖相環結構圖如圖2所示，圖2中，Tαβ為三相到靜止兩相的坐標變換矩陣，LPF為低通濾波器，VCO為鎖相環的壓控振蕩環節.通過雙派克變換的自解耦模型提取電網電壓不平衡條件下的基波正序分量，同時實現了二倍頻的抑制，進一步使有效的基波無功正序分量經過環路濾波器和壓控振蕩器，達到電網電壓不平衡條件下的跟蹤.

圖2 雙派克變換三相鎖相環結構

3 仿真分析

根據上述理論分析，在Matlab/Simulink中搭建了基于雙派克變換的三相鎖相環仿真模型，并與傳統的三相鎖相環進行了對比分析.假設電網電壓為三相不平衡，各相表達式分別為

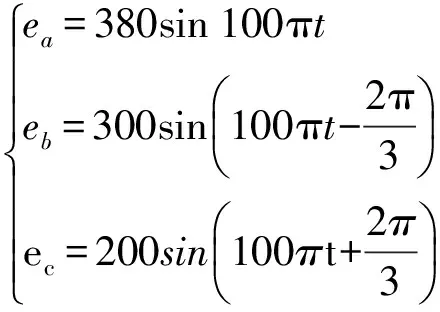
(13)

圖3為輸入的三相不平衡電網電壓波形，圖4為鎖相環輸出的無功直流分量，也即是鎖相環環路濾波器的輸出信號，從圖4中可以看出，針對傳統的三相鎖相環而言，當電網電壓處于不平衡時，會造成環路濾波器的輸出信號含有大量的二次諧波分量，而采用本文提出的雙派克變化自解耦方法能夠有效抑制二倍頻諧波分量，輸出無脈動的直流信號.

圖5和圖6分別為鎖相環輸出頻率和正弦信號的對比分析結果，仿真對比說明，傳統鎖相環在電網不平衡時，輸出頻率因二倍頻分量存在，波動較大，使得輸出的正弦信號也發生畸變，而本文提出的基于雙派克變換的鎖相環具有更好的二倍頻諧波抑制和跟蹤效果，能夠實現鎖相環在電網電壓不平衡條件下的跟蹤.

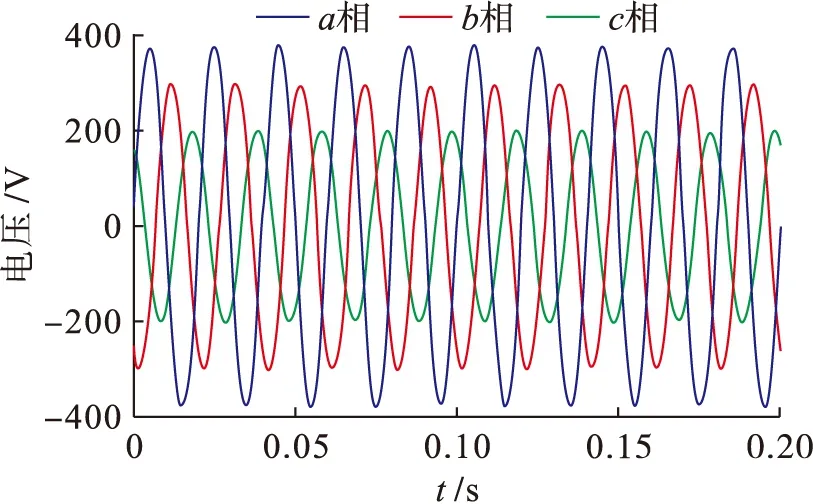
圖3 三相不平衡電網電壓

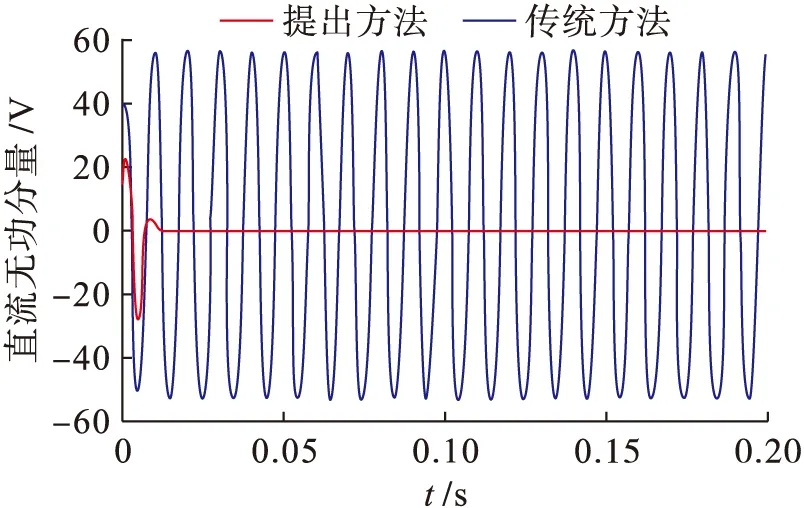
圖4 鎖相環正序無功直流分量

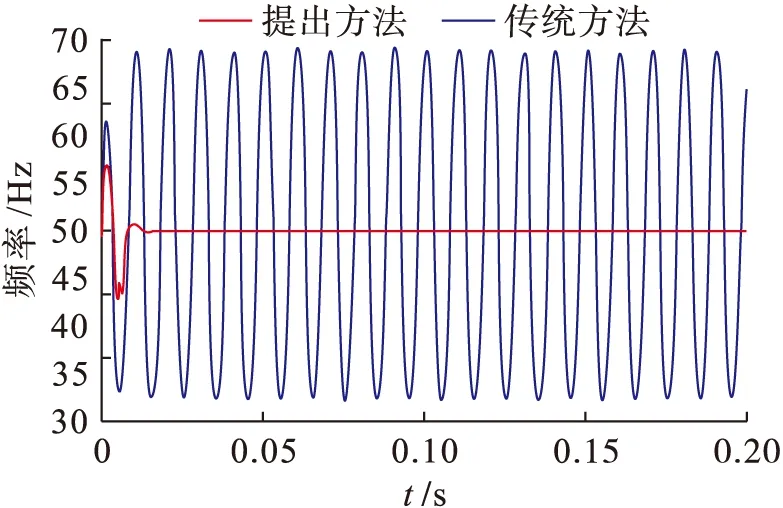
圖5 鎖相環輸出頻率

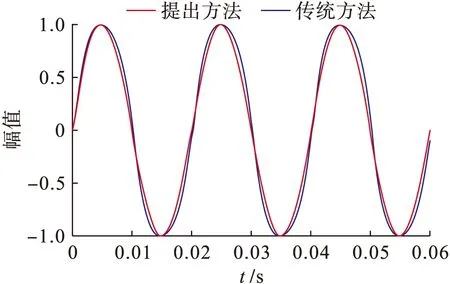
圖6 鎖相環輸出正弦信號

圖7為提出算法鎖相環的輸出相位穩態波形，并將其與幅值縮小的a相電壓波形進行了對比分析(其中仿真圖中a相電壓幅值縮小至了6.2 V).從圖7中可以看出，鎖相環輸出的相位與輸入信號保持了完全的一致，說明提出的鎖相環結構能夠很好地跟蹤輸入信號的相位，穩態誤差較小.

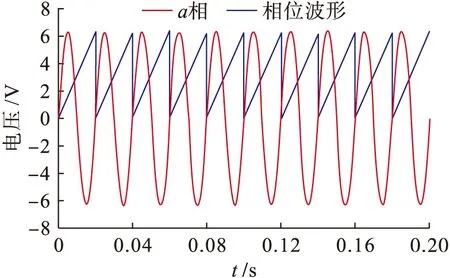
圖7 鎖相環穩態輸出相位

4 結 論

針對傳統鎖相環受電網電壓不平衡影響較大的問題，本文提出一種基于雙派克變換的新型鎖相環技術，鎖相環能夠在電網電壓不平衡時準確地跟蹤電網電壓正序基波分量的相位和頻率，與傳統方法的仿真對比結果驗證了所提新型鎖相環的可行性和有效性，具有一定的借鑒價值.

[1]王寶歸，李澤泉，林勇，等.并網型電力電子裝置數字鎖相環研究 [J].大功率變流技術，2012(4)：39-42.

(WANG Bao-gui，LI Ze-quan，LIN Yong，et al.Study on digital phase-locked loop for grid-connected power electronic device [J].High Power Converter Techno-logy，2012(4)：39-42.)

[2]王湘明，肇文婷.風電并入微網逆變器合成諧波阻抗諧波抑制 [J].沈陽工業大學學報，2014，36(2)：143-148.

(WANG Xiang-ming，ZHAO Wen-ting.Synthesis harmonic impedance for harmonic suppression of wind power micro-grid inverter [J].Journal of Shenyang University of Technology，2014，36(2)：143-148.)

[3]溫華生，謝潮.基于dq變換的三相自適應鎖相環技術 [J].上海電力學院學報，2016，32(2)：151-155.

(WEN Hua-sheng，XIE Chao.Three-phase adaptive phase-locked loop based ondqtransformation [J].Journal of Shanghai University of Electric Power，2016，32(2)：151-155.)

[4]戴永輝，洪巧文，蔡逢煌，等.一種基于多過零鑒相器的數字鎖相環 [J].電源學報，2012(5)：58-62.

(DAI Yong-hui，HONG Qiao-wen，CAI Feng-huang，et al.A DPLL based on multi-zero-crossing phase detector [J].Journal of Power Supply，2012(5)：58-62.)

[5]曹小麗.光伏并網軟件鎖相技術的研究 [D].南昌：南昌航空大學，2013：1-76.

(CAO Xiao-li.The research on software phase locked loop of PV grid-connected generation system [D].Nanchang：Nanchang Hangkong University，2013：1-76.)

[6]袁慶慶，戴鵬，符曉，等.單相電力鎖相環技術綜述 [J].變頻器世界，2010(7)：43-46.

(YUAN Qing-qing，DAI Peng，FU Xiao，et al.An overview of single-phase power phase-locked loop tech-nique [J].The World of Inverters，2010(7)：43-46.)

[7]胡為兵，熊杰.一種新穎的鎖相環的研究 [J].電氣技術，2008(1)：69-71.

(HU Wei-bing，XIONG Jie.Research on a novel phase-locked loop system [J].Electrical Engineering，2008(1)：69-71.)

[8]洪小圓，呂征宇.基于同步參考坐標系的三相數字鎖相環 [J].電工技術學報，2012(11)：203-210.

(HONG Xiao-yuan，Lü Zheng-yu.Research on a novel phase-locked loop system [J].Transactions of China Electrotechnical Society，2012(11)：203-210.)

[9]胡應占，郭素娜.適用于電網不平衡時的廣義積分器鎖相環設計 [J].電力系統保護與控制，2014(11)：148-154.

(HU Ying-zhan，GUO Su-na.Design of generalized integrator phase locked loop for unbalanced grid [J].Power System Protection and Control，2014(11)：148-154.)

[10]閆斌斌，賈焦心.電壓不平衡且畸變下基于平均值環節鎖相環的研究 [J].黑龍江電力，2015，37(6)：483-486.

(YAN Bin-bin，JIA Jiao-xin.Research on phase locked loop based on mean value links under unbalanced and distorted voltage [J].Heilongjiang Electric Power，2015，37(6)：483-486.)

[11]陳國棟，朱淼，蔡旭.一種軟件鎖相環和電壓跌落檢測新算法 [J].中國電機工程學報，2014，34(25)：5385-5394.

(CHEN Guo-dong，ZHU Miao，CAI Xu.A new algorithm for software phase locked-loop and voltage sag detection [J].Proceedings of the CSEE，2014，34(25)：5385-5394.)

[12]江燕興，潘逸菎，竇偉.一種用于光伏并網逆變器的高性能鎖相環設計 [J].電工電能新技術，2016，35(7)：75-80.

(JIANG Yan-xing，PAN Yi-kun，DOU Wei.Design of high-performance phase locked loop used ingrid-connected inverter [J].Advanced Technology of Electrical Engineering and Energy，2016，35(7)：75-80.)

(責任編輯：景 勇 英文審校：尹淑英)

Novel three phase locked loop technique based on double Park transformation

LI Yan-daa，b

(a. School of Physics and Electrical Engineering, b. Henan Photovoltaic Grid Connected Power Generation and Energy Storage Technology Engineering Laboratory, Anyang Normal University, Anyang 455000, China)

Aiming at the problem that the double frequency harmonic perturbation exists in the output of three phase locked loop (PLL) when the power grid voltage has unbalanced fault, a novel PLL based on the double Park transformation was proposed. The positive and negative sequence Park transformation for the voltage signal was carried out, respectively. In addition, the DC component in the negative sequence Park transformation was multiplied by the transformation matrix, and the double frequency component in the positive sequence Park transformation could be eliminated through the cross decoupling. The fundamental positive DC component was effectively extracted, and the accurate tracking of phase and frequency could be realized under the unbalanced grid voltage condition. A simulation model was established in the Matlab/Simulink environment, and the steady state response of PLL under the unbalanced grid voltage was analyzed. The results show that compared with the traditional PLL, the proposed PLL can detect the voltage phase and frequency information more accurately under the grid fault.

phase locked loop (PLL); three-phase unbalance; double-frequency; double Park; positive and negative sequence component; DC component; cross decoupling

2016-09-18.

河南省科技攻關計劃資助項目(152102210294)； 河南省教育廳自然科學研究資助項目(14B470004).

李研達(1982-)，男，河南安陽人，講師，碩士，主要從事光伏發電技術、系統智能控制等方面的研究.

10.7688/j.issn.1000-1646.2017.03.03

TM 615

A

1000-1646(2017)03-0253-05

*本文已于2017-03-28 17∶02在中國知網優先數字出版. 網絡出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20170328.1702.012.html