優化設計在汽車操縱穩定性研究中的應用
謝美芝,蔣銀靜,韋超毅,應文倩
優化設計在汽車操縱穩定性研究中的應用
謝美芝1,蔣銀靜2,韋超毅3,應文倩3
(1.廣西大學土木工程學院,廣西大學工程防災與結構安全教育部重點實驗室,廣西南寧530004;2.廣西機電職業技術學院,廣西南寧530000;3.廣西大學機械工程學院,廣西南寧530004)
汽車的操縱穩定性直接關系到汽車的行駛安全,通過建立線性兩自由度汽車模型,以車輛固有圓頻率為優化目標,車輛前、后輪側偏剛度為設計變量,阻尼比、適度不足轉向為約束條件,建立優化設計數學模型。利用MATLAB優化工具箱,對某車輛進行優化,并對優化前、后車輛的性能進行時域和頻域對比分析。結果表明:優化后汽車的固有圓頻率提高、反應速度加快,且超調量也控制在合理的范圍,為汽車操縱穩定性的研究提供了一個簡捷可行的方法。
操縱穩定性;優化設計;阻尼比;固有圓頻率
操縱穩定性不僅影響到汽車駕駛的操縱方便程度,而且也是決定高速汽車安全行駛的一個主要性能,被稱之為“高速汽車的生命線”。隨著高速公路的飛速發展,對汽車高速行駛的操縱穩定性提出了更高的要求。在研究汽車操縱穩定性時,常把汽車本身看做一個控制系統,按照對控制系統的穩定性、穩態品質和瞬態響應特性的一般要求,來分析和研究汽車的動態特性[1]。超調量、反應時間是系統動態性能中最主要的指標,但這兩者是相互矛盾的。如何兼顧反應時間和超調量,將其控制在合理的范圍之內,是提高汽車操縱穩定性的有效方法。
通過選擇合適的設計變量及目標函數,建立優化設計數學模型,利用MATLAB優化工具箱,對車輛系統進行優化,在保證其具有良好穩定性的基礎上,盡可能地提高其快速響應能力,以及在反應過程中具有良好的平穩性。
1 優化設計數學模型的建立
1.1 目標函數和設計變量
對于一個車輛操縱系統,超調量反映系統響應過程的平穩性,表示執行上的誤差,反應時間則體現了執行速度的快慢,這兩個因素與阻尼比ζ和固有圓頻率ω0的關系是:阻尼比ζ增大,超調量減小,反應時間增大;當阻尼比一定時,固有圓頻率ω0越大,反應時間越短。系統的動態性能由固有圓頻率ω0與阻尼比ζ共同決定。阻尼比ζ為0.5~0.8時,既兼顧了系統的反應時間,又使系統的超調量不至于過大[2]。綜上所述,具有良好穩定性的車輛,其阻尼比應在0.5~0.8之間,且固有圓頻率ω0應盡可能大些[2]。
由Riekert和Schunck提出的線性二自由度模型為汽車動力學理論提供了很好的技術基礎。由線性二自由度的車輛模型[3],可以求出固有圓頻率ω0如下:

式中符號的意義見附表1.
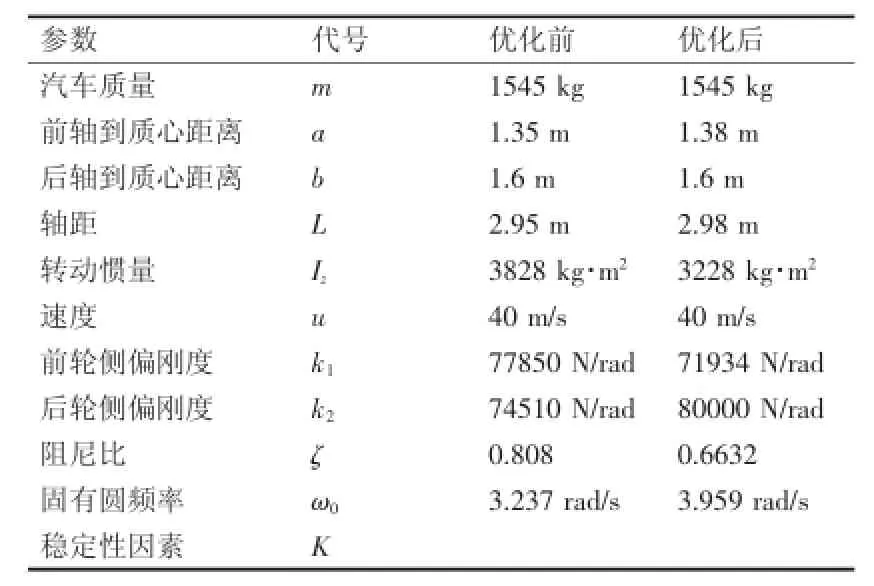
表1 某小車優化前后參數
將固有圓頻率作為優化目標,從式(1)可以看出,汽車的質量m、軸距L,轉動慣量Iz,前、后輪的側偏剛度k1、k2等對目標函數都有影響。從易于實現方面進行考慮,選取汽車前、后車輪的側偏剛度作為設計變量,即設計變量為:X=[x1,x2]T=[k1,k2]T.
優化目標是在滿足0.5≤ζ≤0.8的前提下,使ω0獲得極大值,故目標函數為:
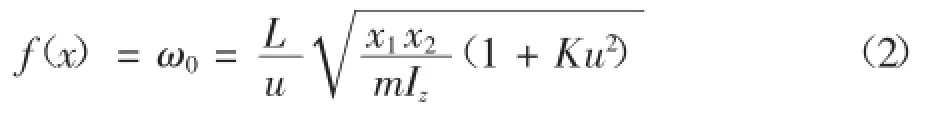
1.2約束條件的確定
約束條件可分為性能約束和邊界約束兩大類,由線性二自由度的車輛模型[3],可以求出阻尼比的表達式為:
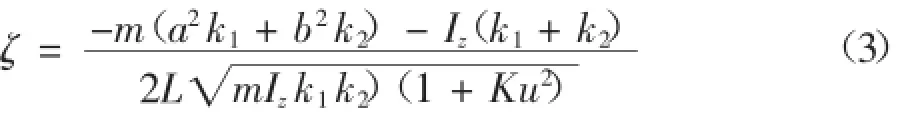
為保證0.5≤ζ≤0.8,可設約束條件為:

過多轉向汽車達到臨界車速時將失去穩定性,故汽車都應具有適度的不足轉向,因此約束條件設為K>0.由可得到性能約束條件為:

小型轎車輪胎的k值約為-28 000~-80 000 N/ rad范圍內[3],因此其邊界約束為:

1.3優化設計數學模型
優化設計的數學模型可表示如下:
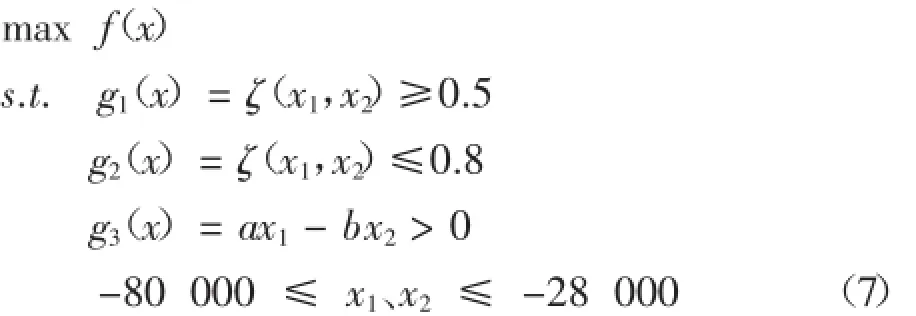
2 最優化問題的MATLAB求解
MATLAB中提供了各種各樣的最優化問題求解函數,可以求解無約束最優化問題、有約束最優化問題及線性規劃、二次規劃問題等。式(7)為有約束非線性最優化問題,可利用MATLAB優化工具箱中的fmincon()函數求解,該函數一般描述為:

該函數在MATLAB中的調用格式為

其中,fun為給M-函數寫的目標函數,x0為初始搜索點,A、b滿足線性不等式約A·x≤b,Aeq、beq滿足等式約束Aeq·x=beq,lb、ub分別為設計變量的上、下邊界,各個矩陣約束如果不存在,則用空矩陣來占位。nonlcon為給非線性約束函數寫的M-文件。options為控制選項。最優化運算完成后,結構將在變量x中返回,最優化的目標函數將在favl變量中返回。fmincon(x)函數常用于求多變量有約束非線性函數的最小值,因此對于求極大值的問題,需乘以-1將其轉換為求極小值問題。
現利用fmincon(x)函數,根據優化設計數學模型式(7),對某小車(其參數見附表1)前、后輪的側偏剛度進行優化。車速按被試汽車最高車速的70%并四舍五入為10的整數倍確定[4],該車最高車速為200 km/h,故優化時的車速選為u=140 km/h.優化后車輛的前、后輪側偏剛度分別為73 917、80 000 N/rad,優化后的阻尼比由原來的0.808降為0.66,可以看出側偏剛度、阻尼比等均在約束范圍之內,且固有圓頻率也由原來的3.237 rad/s提高到3.959 rad/s,說明優化成功。
3 結果分析
3.1優化前、后轉向盤角階躍輸入下的橫擺角速度時域響應對比
在時域里有階躍、單正弦兩種操中輸入。階躍輸入可涉及從線性區值非線性區的很廣領域,是系統動力學中的重要測試函數,因此選擇階躍輸入,即當車輛以恒定速度直線行駛時,駕駛員突然給轉向盤一個很小的角階躍輸入。在MATLAB仿真中,根據已給的狀態方程矩陣A、B、C、D和系統輸入(即前輪轉角)的時間序列信號,應用線性模擬函數語句lsim(A,B,C,D,delta,t)就可以方便地對汽車進行階躍信號輸入仿真,得到橫擺角速度時域響應結果。
從圖1中可以看出,優化前的橫擺角速度超調量較小,但反應時間較長。優化后盡管超調量比優化前的要大,但沒有超過120%,在合理范圍之內,而反應時間卻明顯減小。經計算優化前的反應時間為0.39 s,優化后的反應時間為0.23 s,反應時間縮短了0.16 s,反應速度提高了41%.
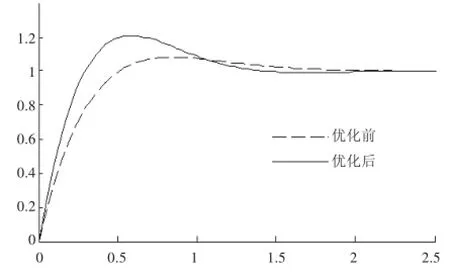
圖1 角階躍輸入下的時域響應對比
3.2優化前、后橫擺角速度頻率響應特性對比
頻率響應特性完整地描述了車輛在小的擾動下的動態性能,而穩態響應則是頻率響應的一個特例,因此頻率響應分析在汽車操縱穩定性分析中尤為重要。在頻域里進行評價時,主要評價指標有:不同頻率下,橫向加速度和橫擺角速度對轉向盤轉角的增益;不同頻率下,橫向加速度和橫擺角速度對轉向盤轉角的相位。一個系統傳遞函數G(s)的幅頻和相頻特性可用伯德(Bode)圖來表達。在MATLAB環境下接采用bode()命令便可得到伯德圖,即

圖2中,從幅頻特性圖可以看出,優化前的頻響曲線沒有明顯的共振峰,即共振時增幅比較小,但也可以看出其共振頻率較低只有1.81 rad/s,而優化后的盡管有了明顯的共振峰,但峰值增幅只有約2 dB,在較理想的范圍之內,且共振峰頻率有了明顯的提高,接近3.34 rad/s.從圖2中的相頻特性圖可以看出,在0~10 rad/s的范圍內,優化后的相位滯后角都有不同程度的減少。
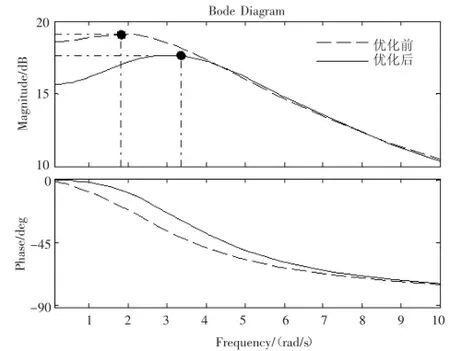
圖2 角階躍輸入下的時域響應對比
4 結束語
通過建立優化設計數學模型,利用MATLAB優化工具箱對某車輛進行優化,并對比優化前、后的性能,結果表明:優化后車輛系統的反應時間縮短了0.16 s,反應速度提高了41%,共振峰頻率提高了1.53 rad/s,在0~10 rad/s的范圍內,優化后的相位滯后角都有不同程度的減少,且超調量也控制在合理的范圍內。在汽車操縱穩定性研究中,選擇恰當的設計變量,合理設置優化目標函數和約束條件,利用MATLAB優化工具箱進行編程計算,可以獲得較為滿意的效果。
[1]宗長富,郭孔輝.汽車操縱穩定性的研究與評價[J].汽車技術,2000(6):6-11.
[2]余志生.汽車理論[M].北京:機械工業出版社,2009.
[3]喻凡,林逸.汽車系統動力學[M].北京:機械工業出版社,2005.
[4]GB/T.6323.3-94.汽車操縱穩定性試驗方法轉向瞬態響應試驗(轉向盤轉角脈沖輸入)[S].
[5]王春香,馮慧忠.MATLAB軟件在機械優化設計中的應用[J].機械設計,2004,21(7):52-54.
[6]梁長飛,李玉光,王淑芬,等.基于Matlab汽車操縱穩定性仿真方法的研究[J].大連大學學報,2014(3):14-18.
[7]白艷,賈鑫,宗長富,等.汽車操縱穩定性客觀評價方法綜述[J].科學技術與工程,2012,12(6):1339-1347.
[8]韋超毅.根軌跡在汽車操縱穩定性研究中的應用[J].農業機械學報,2007(9):20-25.
[9]王正林,王勝開.MATLA B/Simulink與控制系統仿真[M].北京:電子工業出版社,2012.
[10]高國燊.自動控制原理[M].廣州:華南理工大學出版社,2003:62-68.
[11]Pfeffer P E,Harrer M,Johnston D N.Interaction of vehicle and steering system regarding on-centre handling[J].Vehicle System Dynam ics,2008(46):413-428
[12]Ghoneim Y,Lin W,et al.Integrated chassis control system to enhance vehicle stability[J].International Journal of Vehicle Design,2000,23(1/2):124-144.
The Application of Optimization Design in Vehicle Handling Stability Study
XIE Mei-zhi1,JIANG Yin-jing2,WEI Chao-yi3,YING Wen-qian3
(1.College of Civil Engineering and Architecture Guangxi University,Key Laboratory of Disaster Prevention and Structural Safety of the Ministry of Education Guangxi University,Nanning Guangxi 530004,China;2.School of Vehicle Engineering Guangxi Technological College,Nanning Guangxi 530000,China;3.School of Mechanical Engineering Guangxi University,Nanning Guangxi 530004,China)
Car’s steering stability is related to vehicle driving safety directly,the optimum design mathematical model of a car is set up through the two degrees of freedom linear model,while the inherent circular frequency of vehicle as the optimization goal,front and rear wheel cornering stiffness of vehicle as design variables,damping ratio and moderately understeer as constraint conditions.Optimization algorithm of vehicles performance is carried out by using MATLAB optimization toolbox,then compares the vehicles performances of before and after optimization in time domain and frequency domain analysis.Results show that the optimized car’s inherent circular frequency increased,reaction speed improved,and the overshoot of control in a reasonable scope,also provides a simple and feasible method for the research of vehicle handling stability.
steering stability;optimization design;damping ratio;inherent circular frequency
U461.6
A
1672-545X(2017)02-0006-03
2016-11-14
廣西自然科學基金(項目編號:2014GXNSFAA118348),廣西大學實驗教改項目(20140118)
謝美芝(1967-),女,廣西梧州人,副教授,主要研究方向:計算機仿真及CAD。

