冪級數π-Armendariz環

王 堯，李 敏，任艷麗

(1.南京信息工程大學數學與統計學院，江蘇 南京 210044；2.南京曉莊學院信息工程學院，江蘇 南京 211171)

冪級數π-Armendariz環

王 堯1，李 敏1，任艷麗2

(1.南京信息工程大學數學與統計學院，江蘇 南京 210044；2.南京曉莊學院信息工程學院，江蘇 南京 211171)

引入冪級數π-Armendariz環的概念，研究了冪級數π-Armendariz環的擴張，證明了如果環R是具有冪零有界指數的NI環，且為α-容許環，則R[x；α]是冪級數π-Armendariz環.同時討論了冪級數環的冪零p.p.性和弱zip性.

冪級數環；冪級數π-Armendariz環；NI環；弱zip環

1 預備知識

本文假定所研究的環R都是有單位元1的結合環.以R[x]，R[[x]]分別表示R上的多項式環和R上的冪級數環；以nil(R)，P(R)，Nil*(R)，L(R)分別表示環R中所有冪零元的集合、素根、上詣零根和Levitzki根；以Vn(R)表示Dn(R)中矩陣滿足ast=a(s+1)a(t+1)(s=1，…，n-2，t=2，…，n-1)的矩陣子環.一個環R稱為2-素環，如果P(R)=nil(R).環R是2-素環，當且僅當R/P(R)是約化環.

一個環R稱為弱2-素環，如果L(R)=nil(R).一個環R稱為NI環，如果Nil*(R)=nil(R).這幾個環之間的關系是：2-素環?弱2-素環?NI環?詣零冪級數Armendariz.

2 冪級數π-Armendariz環

顯然冪級數π-Armendariz環是冪級數弱Armendariz環.

引理2.1[2]如果R是一個詣零冪級數Armendariz環，則nil(R[[x]])?nil(R)[[x]].

命題2.1 (1) 詣零冪級數Armendariz環是冪級數π-Armendariz環；(2) 冪級數π-Armendariz環的子環是冪級數π-Armendariz環.

(2) 由冪級數π-Armendariz環定義知結論成立.

命題2.2 如果R是一個具有冪零有界指數的環，那么對任意的n≥2，Tn(R)是冪級數π-Armendariz環，當且僅當環R是冪級數π-Armendariz環.

證明 因為R是Tn(R)的子環，所以根據命題2.1(2)知必要性成立.下證充分性.容易驗證Φ：Tn(R)[[x]]→Tn(R[[x]])是典范環同構.

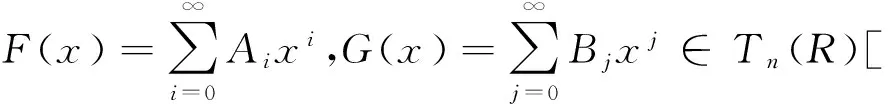
由F(x)G(x)∈nil(Tn(R)[[x]])可得Φ(F(x))Φ(G(x))∈nil(Tn(R)[[x]]).注意到

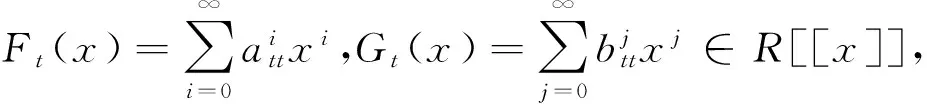
推論2.1 設R是一個具有冪零有界指數的冪級數π-Armendariz環，則對n≥2，下列結論成立：

(1)Dn(R)是冪級數π-Armendariz環；

(2)Vn(R)是冪級數π-Armendariz環；

(3)R(x)/(xn)是冪級數π-Armendariz環.

證明Dn(R)是Tn(R)的子環，Vn(R)是Dn(R)的子環，且R(x)/(xn)?Vn(R)環，由命題2.1(2)知結論成立.

根據命題2.2不禁猜測：環R上的n階全矩陣環Mn(R)是冪級數π-Armendariz環(n≥2).但是下面的例子給出了否定回答.

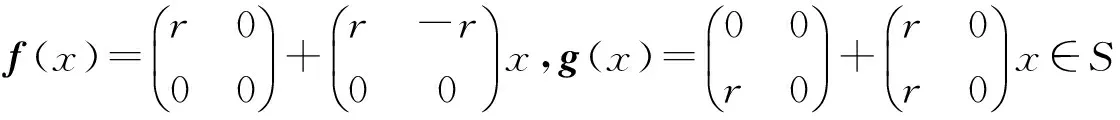
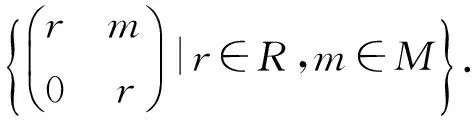
命題2.3 如果R是一個具有冪零有界指數的冪級數π-Armendariz環，則T(R，R)是冪級數π-Armendariz環.

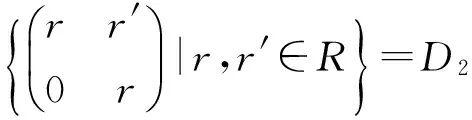
一個環稱為詣零半交換環[7]，如果對a，b∈R，由ab∈nil(R)可以推出aRb∈nil(R).

命題2.4 冪級數π-Armendariz環是詣零半交換環.

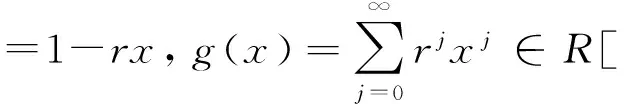
3 冪級數π-Armendariz環更多的例子

命題3.1 設R是一個環，I是R的一個詣零理想.如果R/I是冪級數π-Armendariz環，則R是冪級數π-Armendariz環.

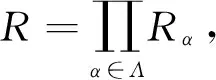
定理3.1中的“所有Rα的冪零有界指數有上界N”的條件是不能去掉的，文獻[8]的例2.7給出了去掉該條件時的反例.

推論3.1 設R是一個環，e∈R是中心冪等元.如果eR和(1-e)R是冪級數π-Armendariz環，則R是冪級數π-Armendariz環.

證明 因為e∈R是中心冪等元，并且R=eR?(1-e)R，所以由定理3.1知結論成立.

定理3.2 設Δ是有限環R中的由中心正則元構成的乘法封閉子集，則Δ-1R是冪級數π-Armendariz環，當且僅當R是冪級數π-Armendariz環.

故f(x)g(x)∈nil(R[[x]]).

由于R是冪級數π-Armendariz環，所以aibj∈nil(R)(?i，j)，從而αiβj=(uv)-1aibj∈nil(Δ-1R)，Δ-1R是冪級數π-Armendariz環.

必要性.因為R是Δ-1R的子環，據命題2.1(2)知結論成立.

引理3.1 如果R是一個具有冪零有界指數的NI環，則nil(R[[x]])=nil(R)[[x]].

證明 如果環R是一個具有冪零有界指數的NI環，則nil(R)是一個具有冪零有界指數的詣零環.根據文獻[3]知nil(R)[[x]]是詣零的，因此nil(R[[x]])?nil(R)[[x]].又由引理2.1知nil(R[[x]])?nil(R)[[x]]，故nil(R[[x]])=nil(R)[[x]].

命題3.2 如果R是一個具有冪零有界指數的NI環，則R[[x]]是詣零半交換環.

命題3.3 如果R是有限環，則R[x]是冪級數π-Armendariz環，當且僅當R[x；x-1]是冪級數π-Armendariz環.

證明 令Δ={1，x，x2，…}，則Δ是環R[x]中的乘法封閉子集.因為R[x；x-1]=Δ-1R[x]，所以根據定理3.2知結論成立.

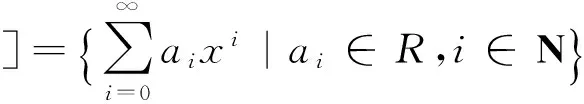
引理3.2 如果環R是α-容許環，則對任意的a，b∈R，ab∈nil(R)當且僅當aαk(b)∈nil(R)，其中k為任意正整數.

證明 由文獻[9]之引理2.8即知充分性成立.

必要性.只需證明aα(b)∈nil(R)即可.因為ab∈nil(R)，所以存在正整數n使得(ab)n=0.因為環R是α-容許環，所以aα(bab…ab)=0，aα(b)α(ab…ab)=0，從而aα(b)ab…ab=0.由aα(b)aα(b…ab)=0可得aα(b)aα(b)ab…ab=0.重復利用R是α-容許環的性質可得(aα(b))n=0，故有aα(b)∈nil(R)，aαk(b)∈nil(R).

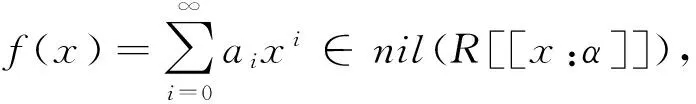
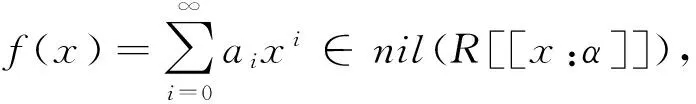
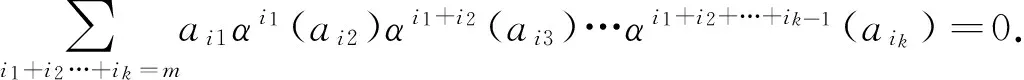
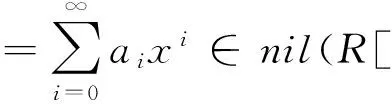
定理3.3 設R是α-容許環的NI環.如果環R是具有冪零有界指數的NI環，則R[x；α]是冪級數π-Armendariz環.

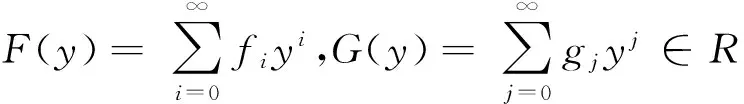
U(x)=f0+f1xk1+f2xk2+…+fnxkn+…∈R[[x；α]]，

V(x)=g0+g1xk1+g2xk2+…+gnxkn+…∈R[[x；α]].

從而

U(x)=a00+a01x+a02x2+…+a0txt+a10xk1+a11xk1+1+a12xk1+2+…+
a1txk1+t+…+an0xkn+an1xkn+1+an2xkn+2+…+antxkn+t+…∈R[[x；α]]，

V(x)=b00+b01x+b02x2+…+b0hxh+b10xh1+b11xk1+1+b12xk1+2+…+
b1hxk1+h+…+bn0xkn+bn1xkn+1+bn2xkn+2+…+anhxkn+h+…∈R[[x；α]].

由kn的取法知U(x)是包含所有fi系數的冪級數，V(x)是包含gi系數的冪級數.因為F(y)G(y)∈nil(R[x；α][[y]])，所以U(x)V(x)∈nil(R[x；α]).R是α-容許環和NI環，從而由文獻[2]和命題3.4知aisαis∈nil(R).又由引理3.3知fi(x)gi(x)∈nil(R[x；α])，所以R[x；α]是冪級數π-Armendariz環.

推論3.2 如果環R是一個具有冪零有界指數的NI環，則R[x]是冪級數π-Armendariz環.

4 冪級數環的冪零p.p.性和弱zip性

對于環R的任一非空子集X，稱NrR(X)={r∈R|Xr∈nil(R)}為X在環R中的弱零化子.稱一個環R為冪零p.p.環，對任意的p?nil(R)，如果NrR(p)(作為右理想)是由一個冪零元生成的.稱一個環R是弱zip環，對于環R的任一非空子集X?R，如果NrR(X)?nil(R)，則一定存在一個有限子集Y?X，使得NrR(Y)?nil(R).稱一個環R是左弱zip環，對于環R的任一非空子集L?R，如果NrR(L)?nil(R)，則一定存在一個有限子集H?L，使得NrR(H)?nil(R).如果環R既是右弱zip環又是左弱zip環，則稱環R為弱zip環.

命題4.1 設R是具有冪零有界指數的NI環.如果環R是一個冪零p.p.環，則R[[x]]是一個冪零p.p.環.

證明 任取F=a0+a1x+a2x2+…+anxn+…?nil(R[[x]])，對任意的G=b0+b1x+b2x2+…+bmxm+…∈NrR[[x]](F)，則有FG?nil(R[[x]]).由引理3.1知FG?nil(R)[[x]]且環R為NI環，故由文獻[2]之定理1，對任意的i，j，aibj∈nil(R).因為F?nil(R[[x]])=nil(R)[[x]]，所以存在i使得ai?nil(R).再由環R是p.p.環，存在c∈nil(R)使得NrR(ai)=cR.下面證明NrR[[x]](F)=cR[[x]].任取H=c0+c1x+c2x2+…+cpxp+…?R[[x]]，因為c∈nil(R)且NI環的nil(R)是環R的一個理想，故對任意的i，j，aiccj∈nil(R)，即FcH∈nil(R)[[x]]=nil(R[[x]])，從而證明了cR[[x]]∈NrR[[x]](F).另一方面，因為bj∈NrR(ai)=cR，存在rj∈R使得bj=crj.又由G=b0+b1x+b2x2+…+bmxm+…∈NrR[[x]](F)，所以G=cr0+cr1x+cr2x2+…+crmxm+…=c(r0+r1x+r2x2+…+rmxm+…)∈cR[[x]]，即NrR[[x]](F)?cR[[x]].故NrR[[x]](F)=cR[[x]]，其中c∈nil([[R]]).

命題4.2 設R是具有冪零有界指數的NI環，則環R是一個弱zip環，當且僅當R[[x]]是一個弱zip環.

證明 必要性.假設環R是一個zip環，任取R[[x]]的一個非空子集X且滿足NrR[[x]](F)?nil(R[[x]])，令Y表示X中所有元素的系數構成的集合.如果r∈NrR(Y)，則對任意的y∈Y，都有yr∈nil(R)，從而對任意的F=a0+a1x+a2x2+…+anxn+…∈X，air∈nil(R).由引理3.1知Fr∈nil(R[[x]])，r∈NrR[[x]](X)?nil(R[[x]]).這就證明了r∈nil(R)，從而NrR(Y)?nil(R).因為環R是一個弱zip環，存在一個有限子集Y0?Y使得NrR(Y0)?nil(R).?a∈Y0，存在Fa∈X使得Fa的某個系數為a.令X0是對任意的a∈Y0且滿足Fa∈X0的X的極小子集，則X0是X的一個有限子集.設Y1表示X0中所有元素系數構成的集合，則Y0?Y1，進而NrR(Y1)?NrR(Y0)?nil(R).如果G=b0+b1x+b2x2+…+bmxm+…∈NrR[[x]](X0)，則對任意的F=a0+a1x+a2x2+…+anxn+…∈X，FG∈nil(R[[x]])，再由引理3.1知FG∈nil(R)[[x]].因為環R為NI環，由文獻[2]之定理1知aibj∈nil(R)，?i，j.對任意的j，bj∈NrR(Y1)?nil(R)，從而由引理3.1知nil(R)[[x]]=nil(R[[x]])，故G∈nil(R[[x]])，即NrR[[x]](X0)?nil(R[[x]]).因此R[[x]]是一個弱zip環.

充分性.假設R[[x]]是一個弱zip環，任取環R的非空子集Y?R并滿足NrR(Y)∈nil(R).如果F=a0+a1x+a2x2+…+anxn+…∈NrR[[x]](Y)，則對任意的y∈Y，yF=ya0+ya1x+ya2x2+…+yanxn+…∈nil(R[[x]])，再由引理3.1知yF∈nil(R)[[x]].因為環R為NI環，由文獻[2]知yai∈nil(R)，即ai∈NrR(Y).因此對任意的i，ai∈nil(R)，故F∈nil(R[[x]])，從而NrR[[x]](Y)?nil(R[[x]]).因為R[[x]]是一個弱zip環，存在一個有限子集Y0?Y1使得NrR[[x]](Y0)∈nil(R[[x]])，從而NrR(Y0)=NrR[[x]](Y0)∩R?nil(R)，故R是一個弱zip環.

[1] KIM N K，LEE K H，LEE Y.Power series rings satisfying a zero divisor property[J].Comm Algebra，2006，34(6)：2205-2218.

[2] HIZEM S.A note on nil power serieswise Armendariz rings[J].Rendiconti del Circolo Matematico di Palermo，2010，59(1)：87-99.

[3] HUH C，KIM C O，KIM E J，et al.Nilradicals of power series rings and nil power series rings [J].J Korean Math Soc，2005，42(5)：1003-1015.

[4] HUH C，KIM H K，LEE D S，et al.Prime radicals of formal power series rings[J].Bull Korean Math Soc，2001，38(4)：623-633.

[5] NASR-ISFAHANI A，MOUSSAVI A.On skew power serieswise Armendariz rings[J].Comm Algebra，2011，39(9)：3114-3132.

[6] HONG C Y，KIM N K，KWAK T K.Nilradicals of skew power series rings[J].Bull Korean Math Soc，2004，41(3)：507-519.

[7] CHEN W X.On nil-semicommutative rings[J].Thai J Math，2011，9(1)：39-47.

[8] HUH C，LEE C I，PARK K S，et al.Onπ-Armendarizrings[J].Bull Korean Math Soc，2007，44(4)：641-649.

[9] OUYANG L，CHEN H.On weak symmetric rings[J].Comm Algebra，2010，38(2)：697-713.

[10] SZASA F A.Radicals of rings [M].New York：John Wiley and Sons，1981：18-193.

(責任編輯：李亞軍)

Power seriesπ-Armendariz rings

WANG Yao1，LI Min1，REN Yan-li2

(1.School of Mathematics and Statistics，Nanjing University of Information Science and Technology，Nanjing 210044，China；2.School of Information Engineering，Nanjing Xiaozhuang University，Nanjing 211171，China)

The concept of a power seriesπ-Armendariz ring is proposed.The extensions ofπ-Armendariz rings are studied which shows that ifRis of bounded index，an NI ring andα-compatible，thenR[x；α] isπ-Armendariz.Meanwhile，the nilpotent p.p. property and weak zip property of a power series ring are given.

power series ring；power seriesπ-Armendariz ring；NI ring；weak zip ring

1000-1832(2017)02-0015-06

10.16163/j.cnki.22-1123/n.2017.02.004

2015-12-11

國家自然科學基金資助項目(11071097)；江蘇省自然科學基金資助項目(BK20141476).

王堯(1962—)，男，博士，教授，主要從事環論研究；通信作者：任艷麗(1965—)，女，碩士，教授，主要從事環論研究.

O 153.3 [學科代碼] 110·2104

A